Trave Vierendeel

TRAVE VIERENDEEL

In questo esercizio analizziamo una trave Vierendeel, ovvero una trave composta da due correnti collegati da montanti verticali con nodi ad incastro.

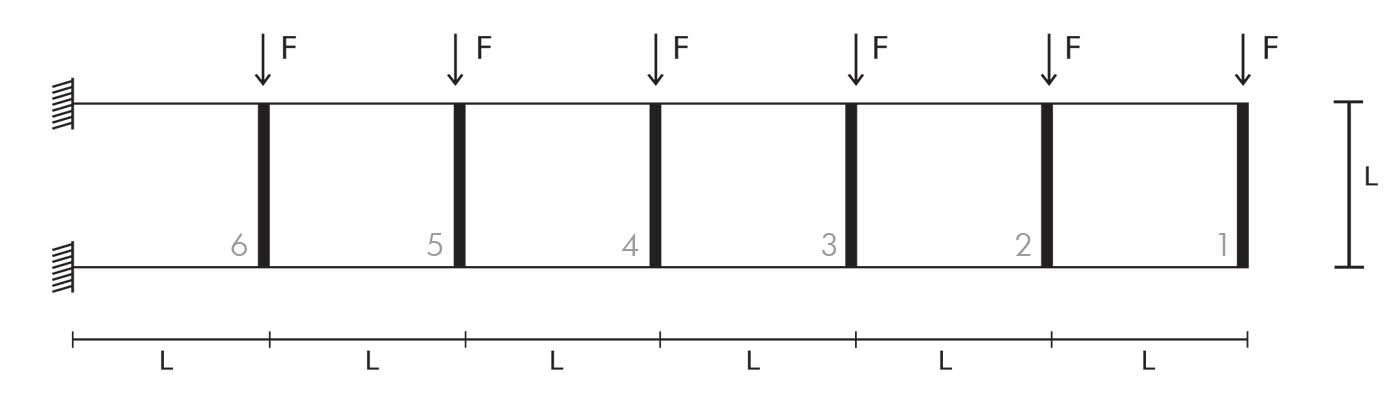
Si tratta dunque di una struttura internamente iperstatica e per risolverla possiamo considerare i montati infinitamente rigidi impedendo qualsiasi tipo di deformazione. In questo modo i collegamenti verticali non possono far altro che traslare verticalmente imprimendo una deformazione nei correnti orizzontali.

Lo studio di questa trave è dunque assimilabile a quello di un modello “shear type” dal quale riprenderemo i metodi di analisi.

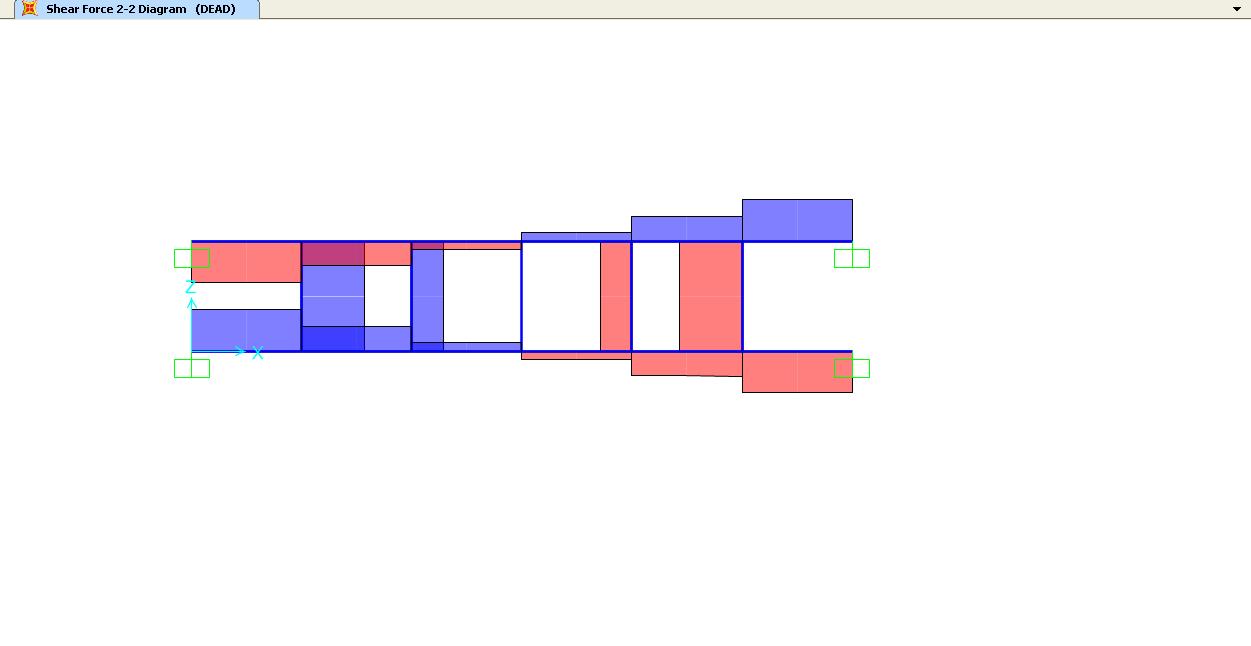
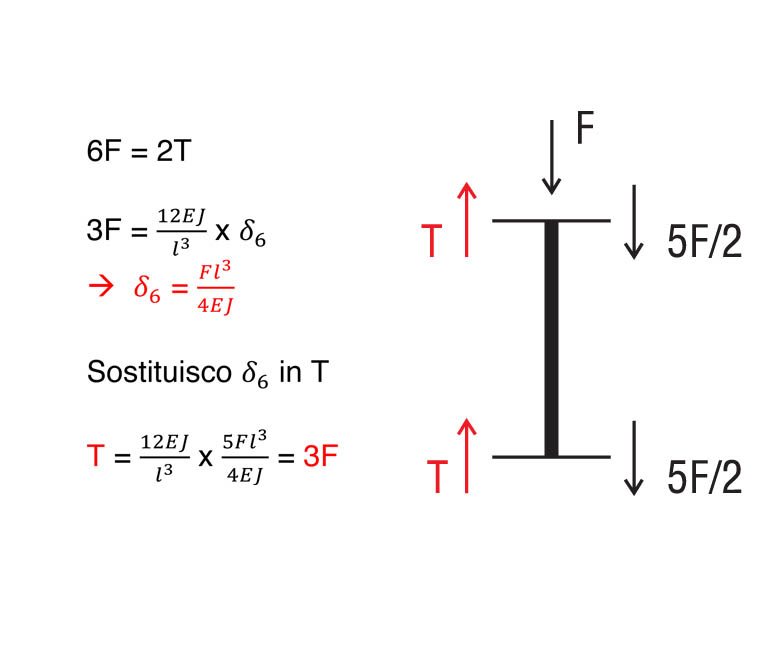
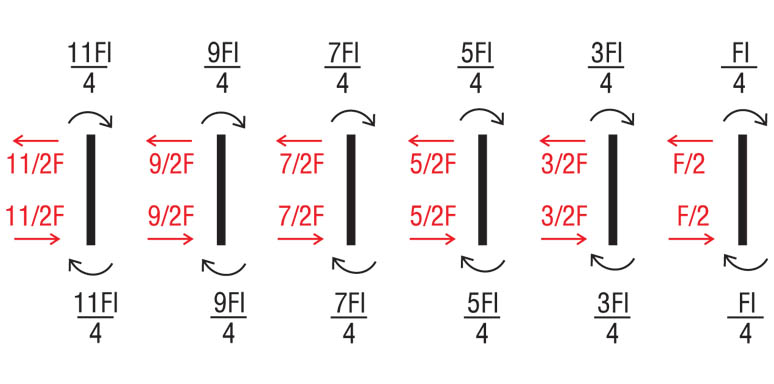
Iniziamo con il calcolo delle reazioni di taglio del corrente orizzontale grazie all’equazione di equilibrio alla traslazione che eseguiremo separatamente in ognuno dei sei tratti.

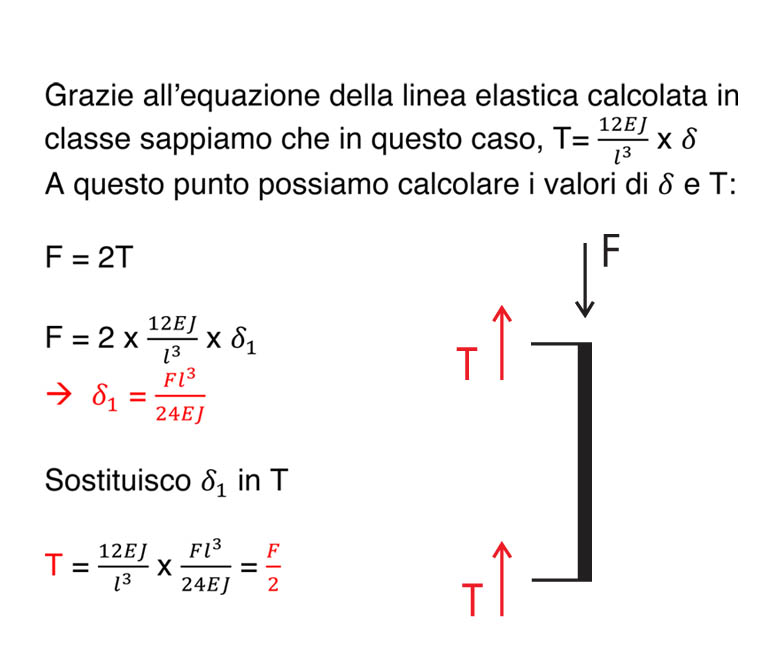
tratto 2:

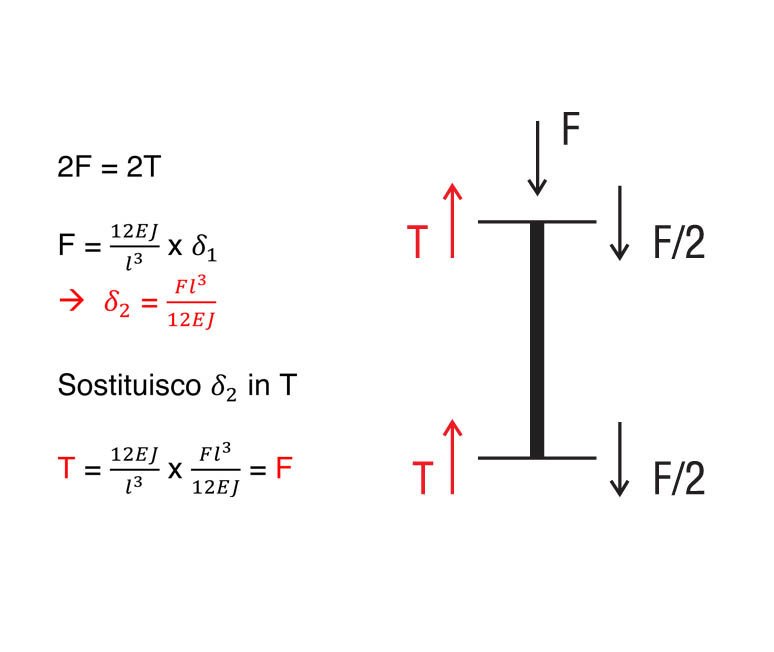
tratto 3:

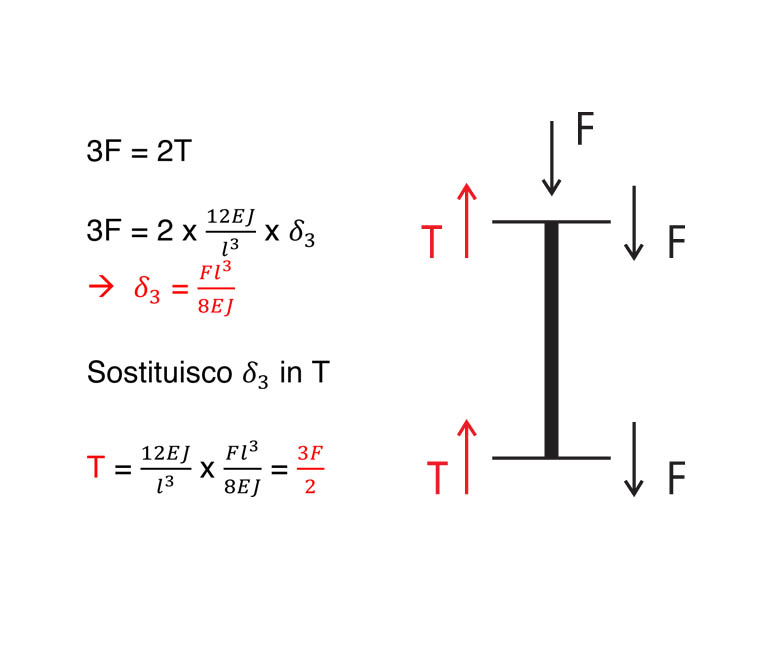
tratto 4:

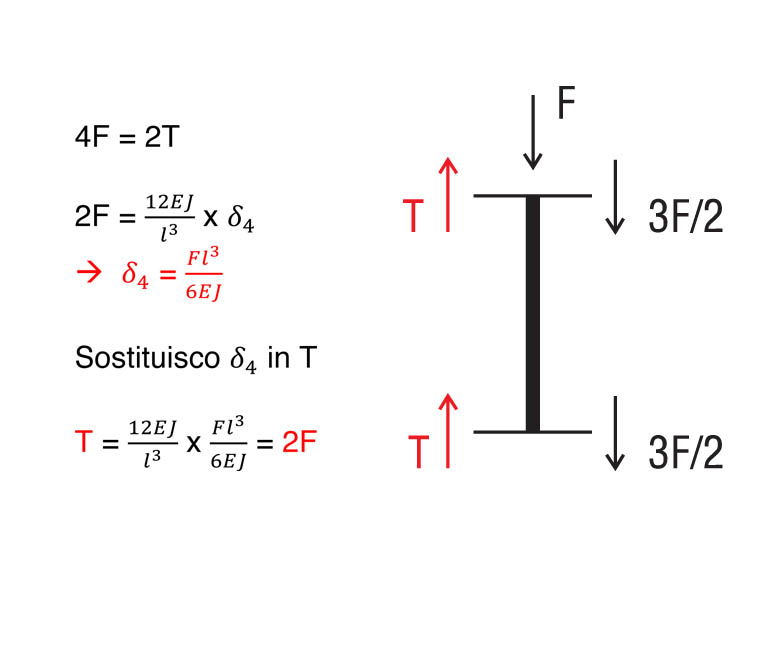
tratto 5:

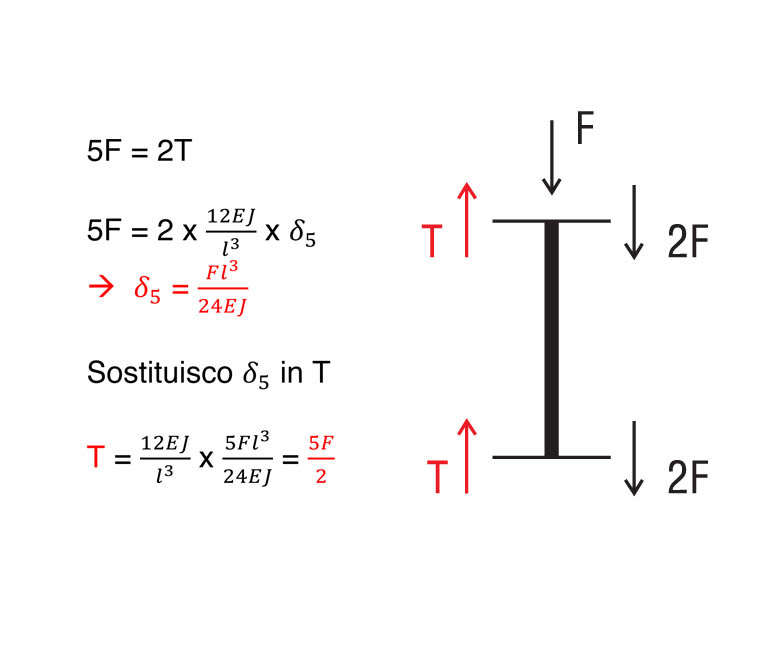
tratto 6:

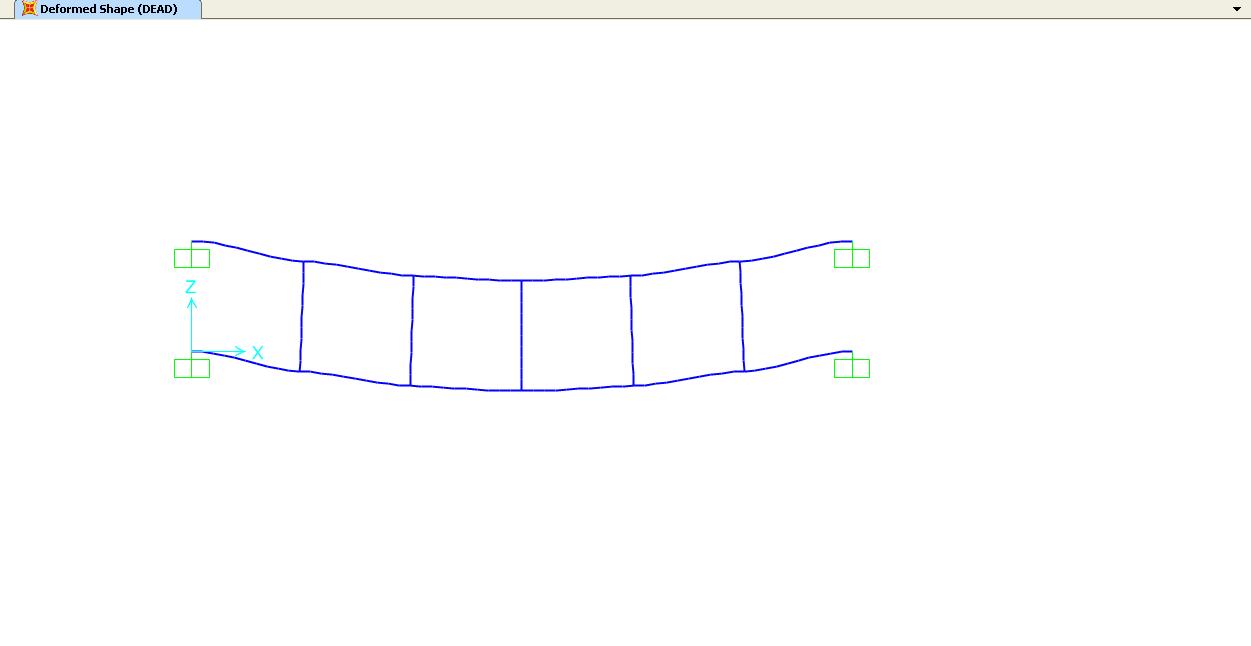
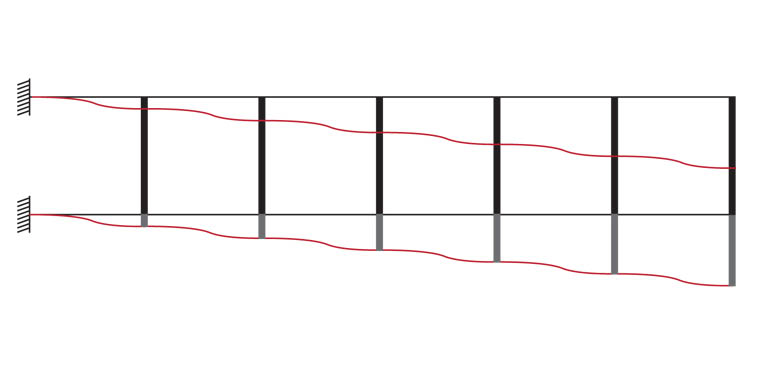
Disegno la deformata:

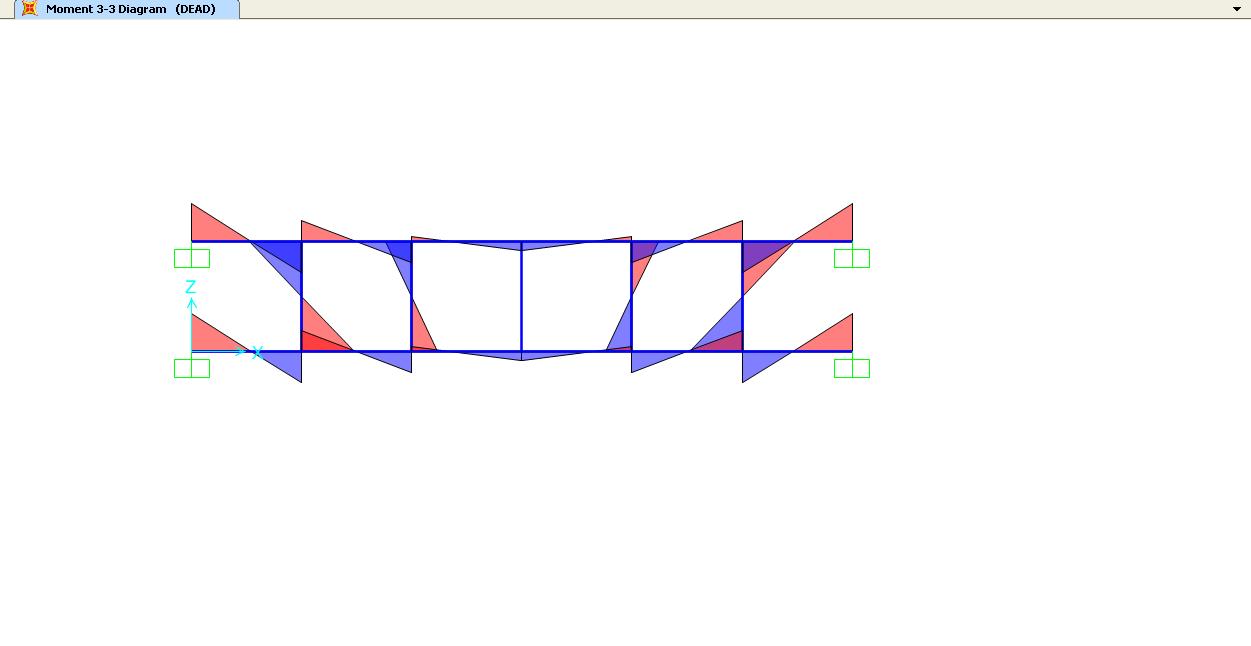
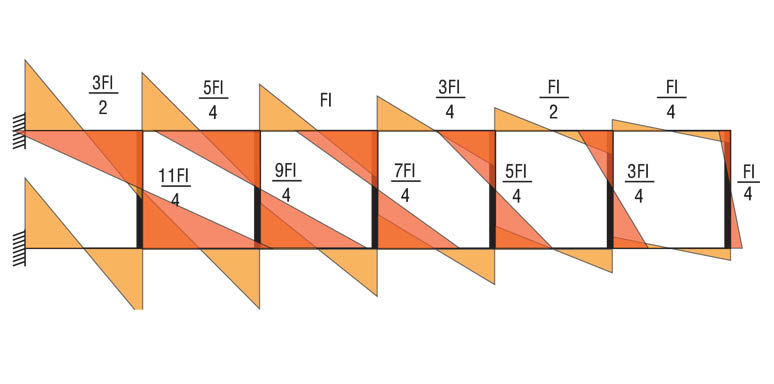
Per capire il diagramma del momento dei correnti orizzontali, possiamo osservare lo schema della deformata il quale ci indica che il punto di curvatura nullo (e di conseguenza il punto in qui il momento è pari a zero) si trova in mezzeria. Quindi possiamo capire che il valore del momento agli estremi delle aste orizzontali sarà pari al valore del taglio ricavato, moltiplicato per il braccio l/2.

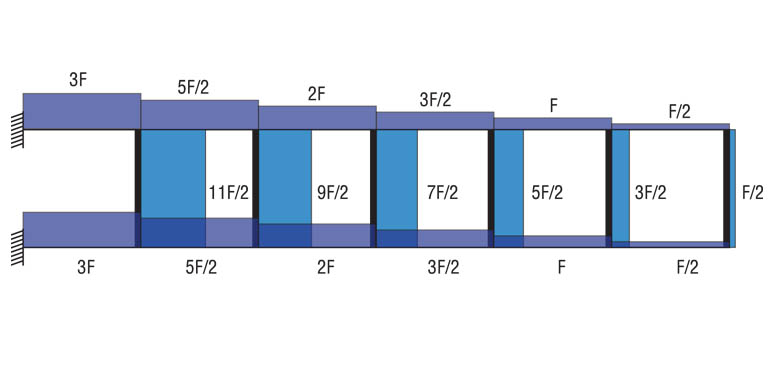
Ora bisogna calcolare il valore del momento e del taglio delle aste verticali.

I momenti li troviamo facendo l’equilibrio alla rotazione delle aste verticali.

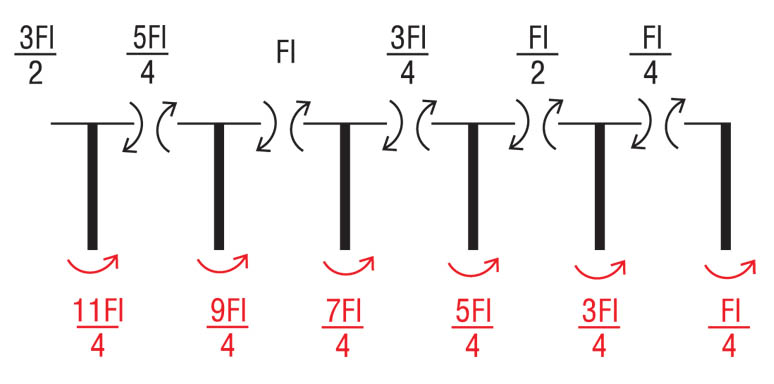
Il taglio va trovato equilibrando ai momenti appena ricavati una coppia di forze. 

Per finire i due diagrammi:

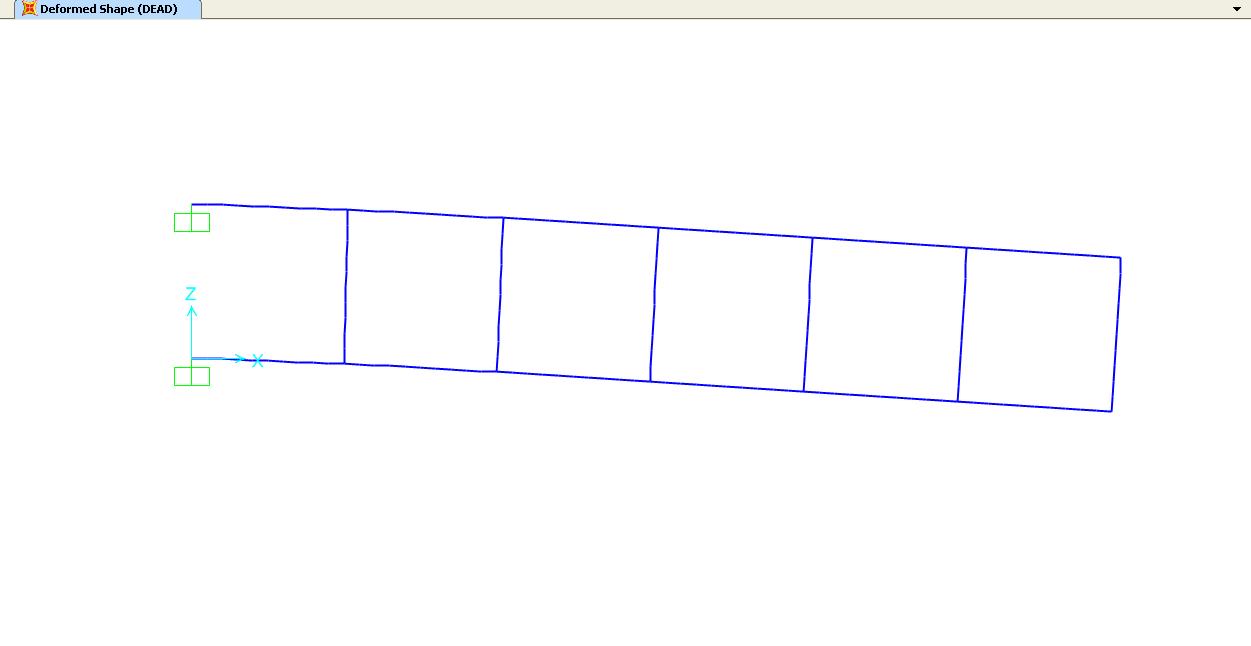
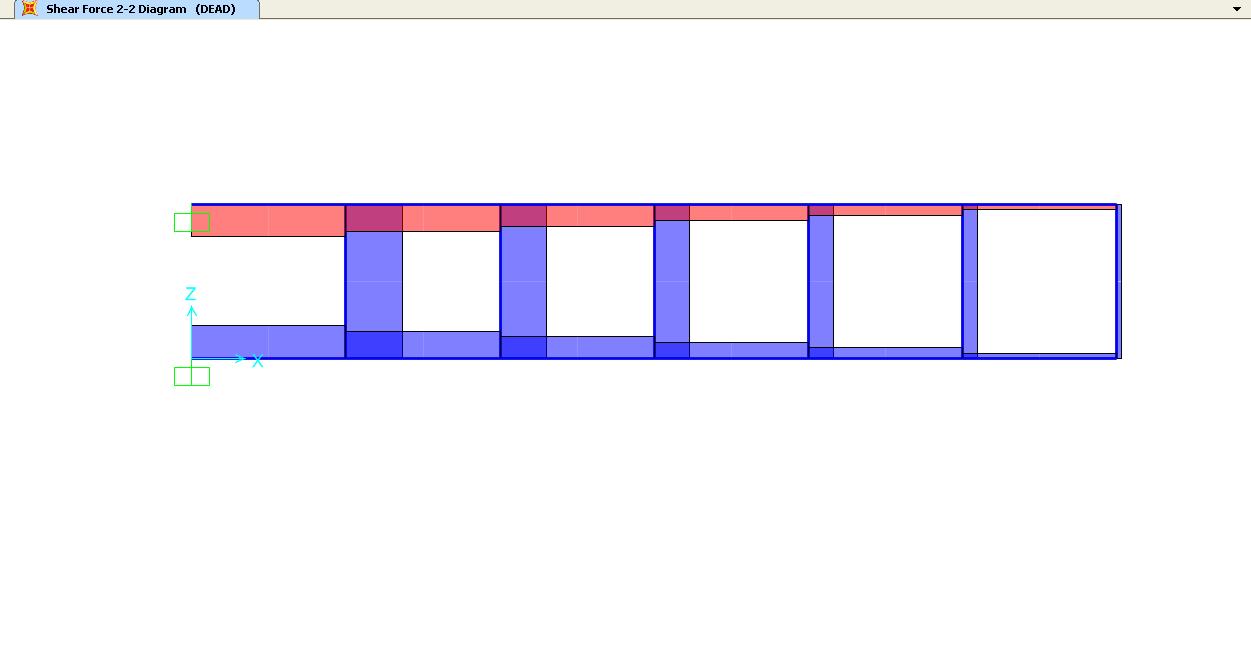
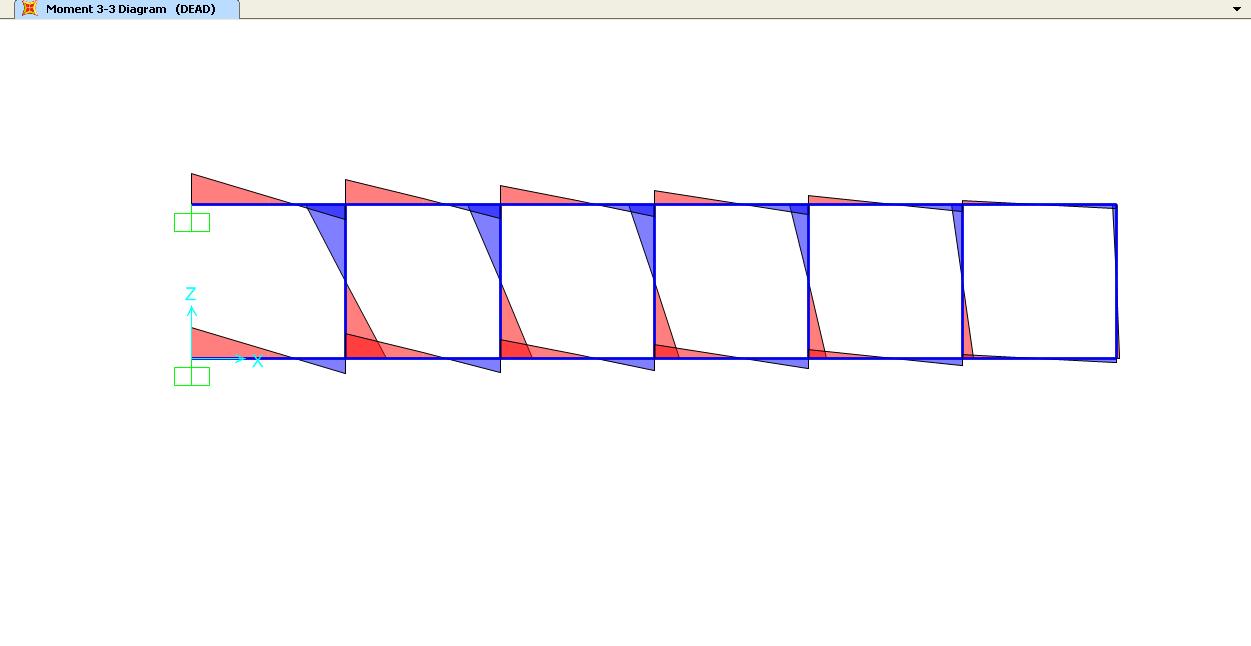
Confronto i risultati con SAP:

TRAVE VIERENDEEL DOPPIAMENTE APPOGGIATA

Questa volta analizzeremo nuovamente la trave vierendeel con la differenza che verrà vincolata in entrambi i bordi, e come in precedenza ci ricaveremo i valori di taglio, momento e spostamento di tutte le aste.

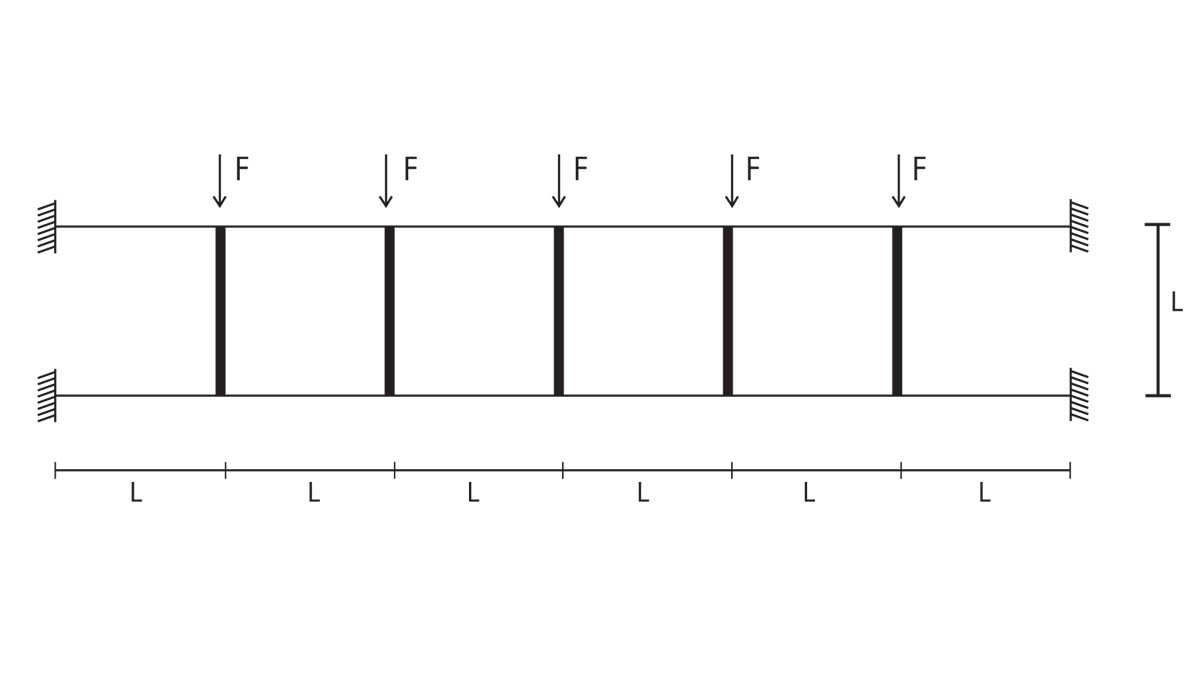
Notiamo come a differenza di prima, la struttura è perfettamente simmetrica, un aspetto che ci semplifichera molto i calcoli!

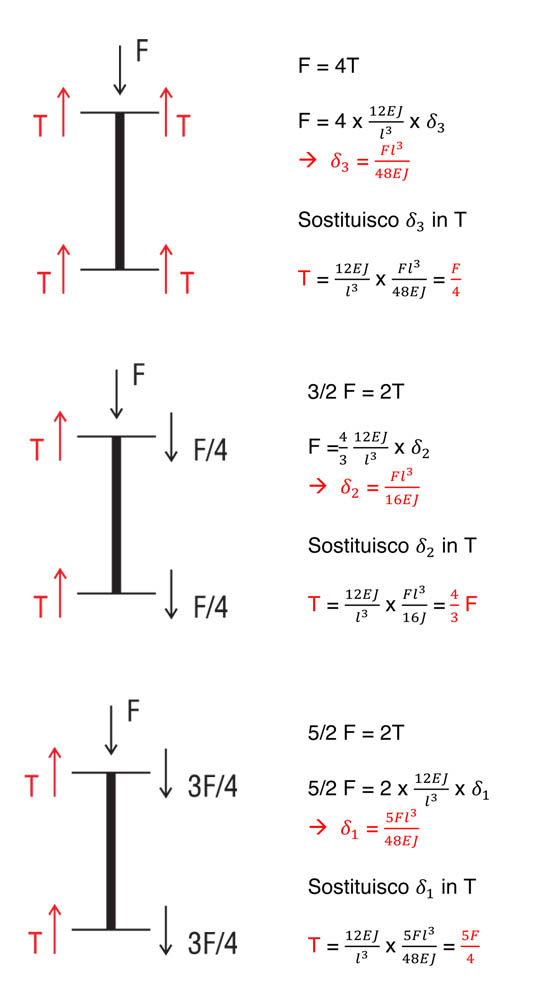
Partendo dal tratto centrale, analizziamo le reazioni alle forze verticali:

(come prima per ricavare il momento dei correnti orizzontali basta moltiplicare il valore del taglio per l/2)

disegno la deformata:

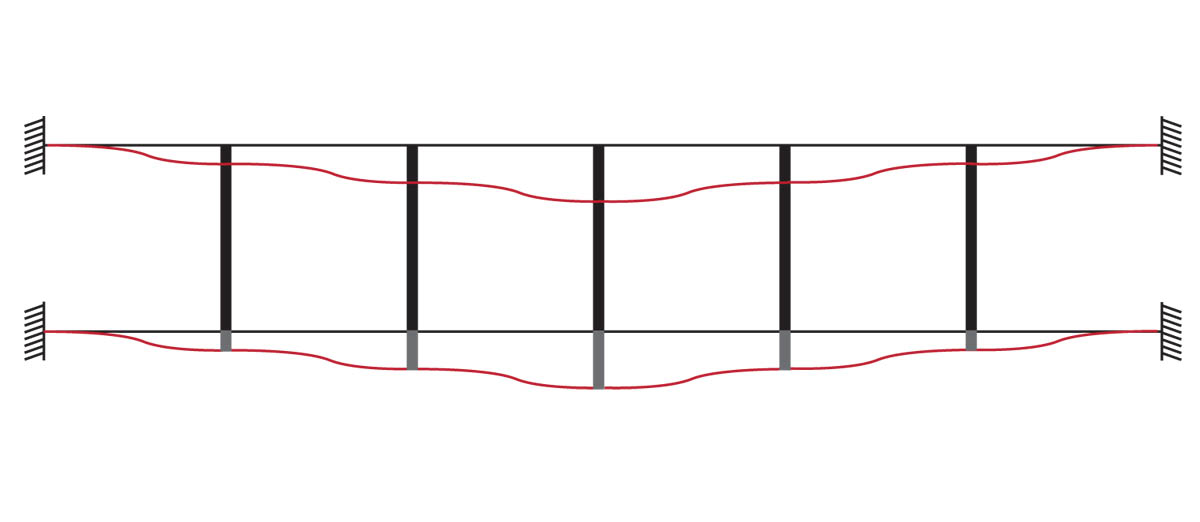
Equilibrio al nodo per ricavare il valore del momento delle aste verticali:

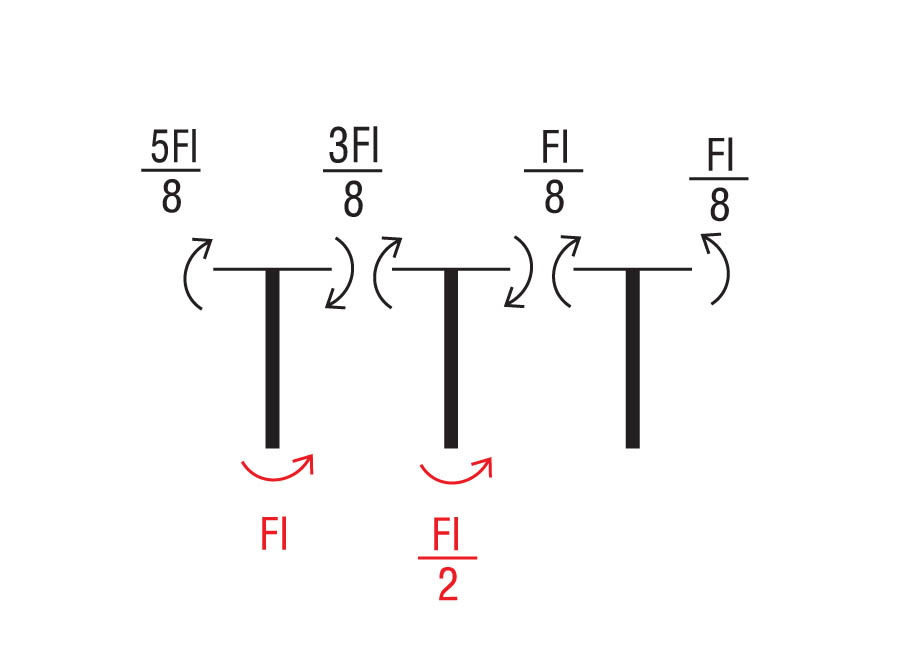
Equilibrio delle aste verticali per calcolare il valore del taglio:

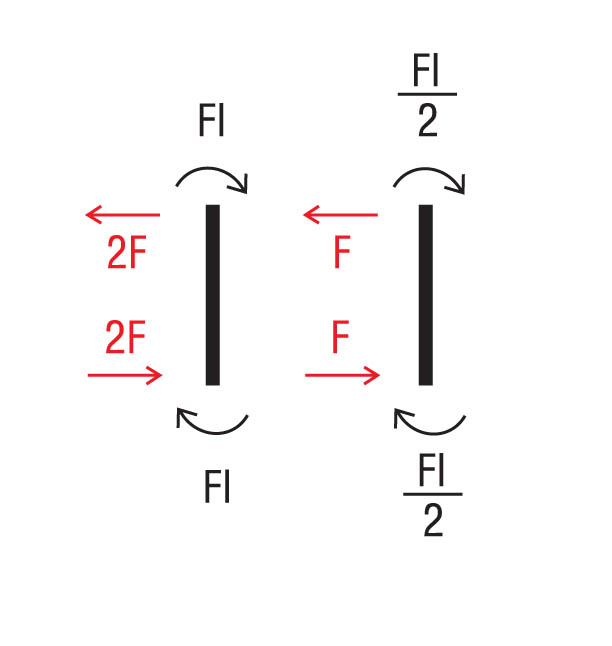
Diagramma del taglio:

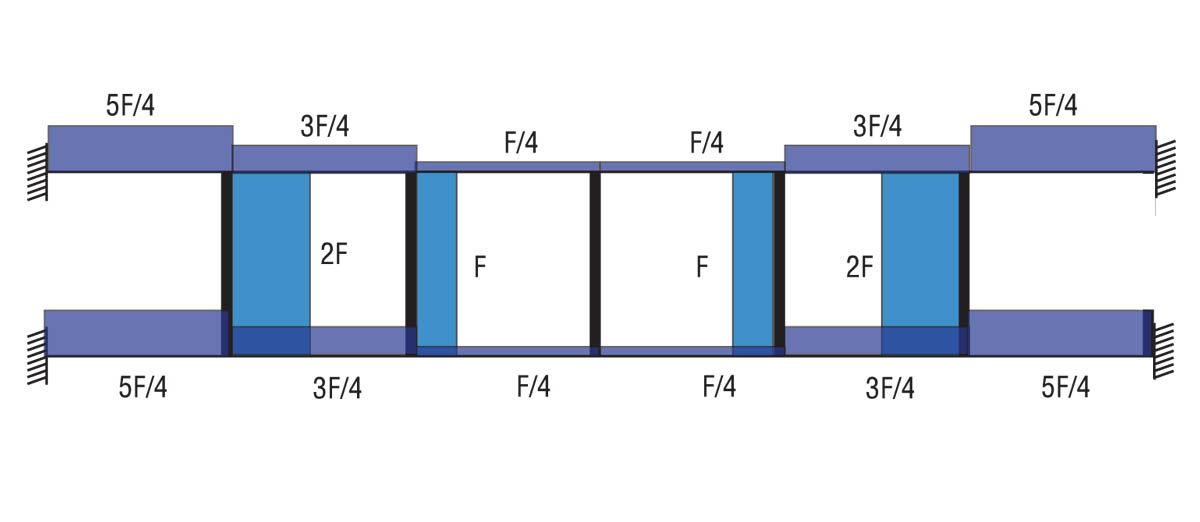
Diagramma del momento:

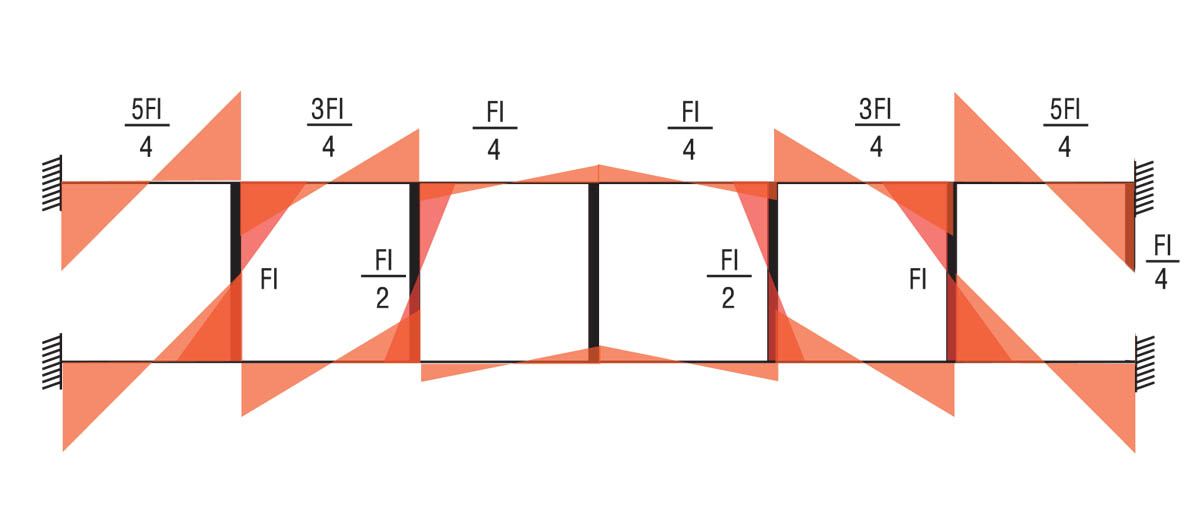
Confronto i risultati con SAP: