esercitazione_Rigidezza torsionale

ESERCIZIO 1:

In questa prima esercitazione studieremo il comportamento torsionale di una struttura iperstatica in tre dimensioni, per poi verificarla tramite SAP2000.

Si tratta dunque di un telaio composto da tre aste vincolate ad incastro e da un'asta a sbalzosulla quale è applicato un carico distribuito q (10KN). Inoltre la struttura è 12 volte iperstatica (in 3d un incastro conta 6 gradi di vincolo) considerando 18 gdv e 6 gdl.

Lo sbalzo è di per sè isostatico quindi studiando i diagrammi delle sollecitazini, possiamo vedere come effetivamente esso sul nodo e possiamo sostituire la mensola con un momento (ricordiamo che consideriamo il pilastro assialmente indeformabile, possiamo perciò escludere l'azione dello sforzo normale).

Questo momento provoca una rotazione delle tre aste, creando due reazioni differenti: le due aste complanari reafiranno tramite la rigidezza flessionale e l'asta "perpendicolare" con la rigidezza torsionale. A questo punto possiamo risolvere l'iperstaticità delle struttura grazie al metodo della linea elastica:

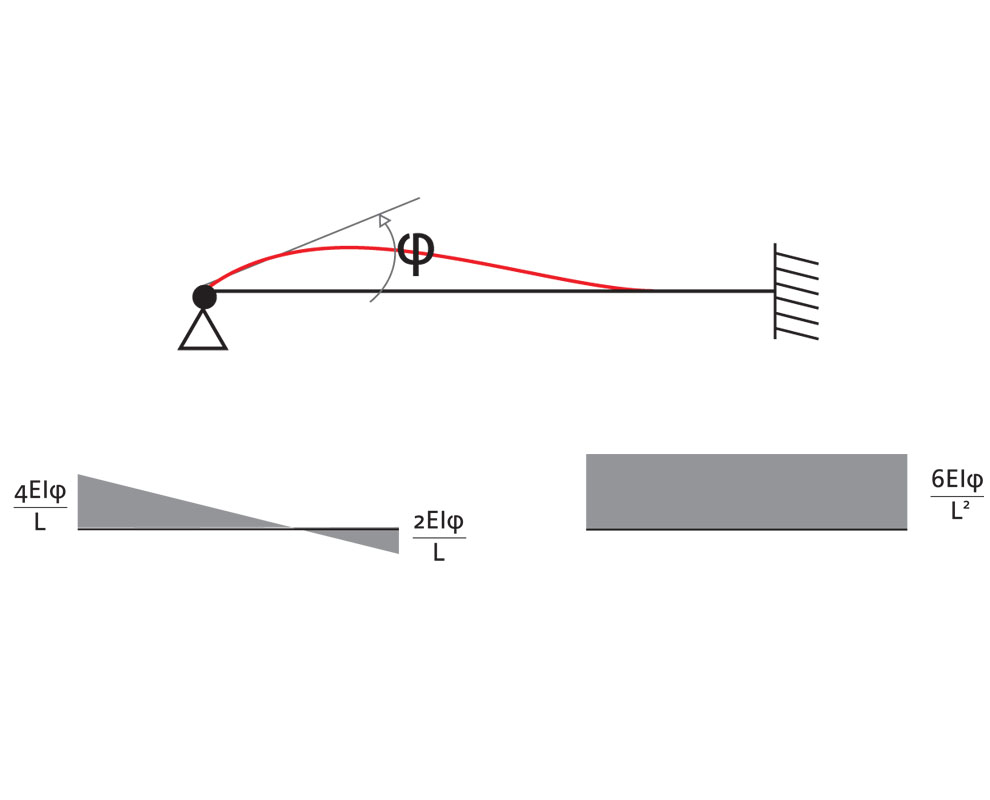
riportiamo i momenti ricavati dall'eq. della inea elastica:

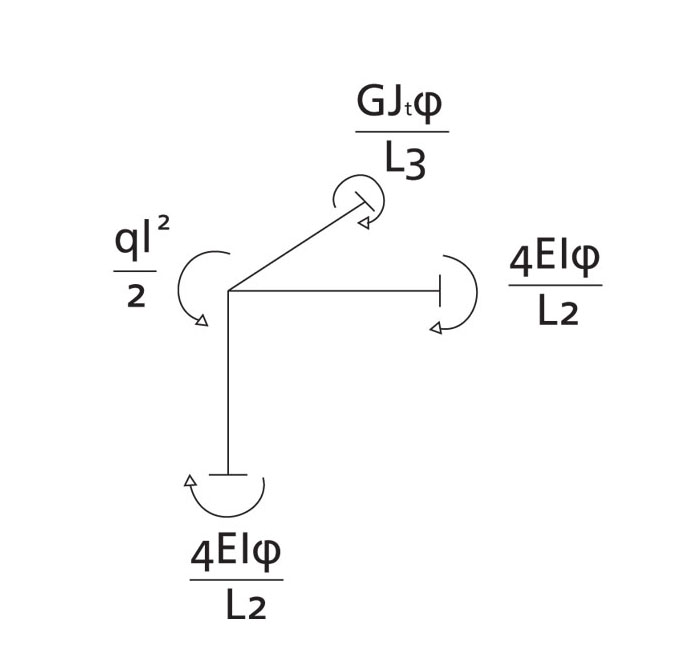
Equilibrio alla rotazione:

Mi ricavo la rigidezza (dove Ra è la somma delle rigidezze):

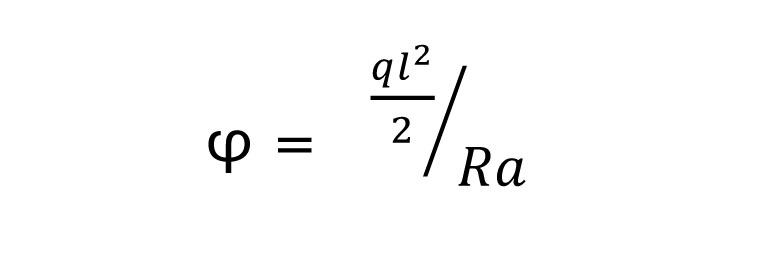
I momenti:

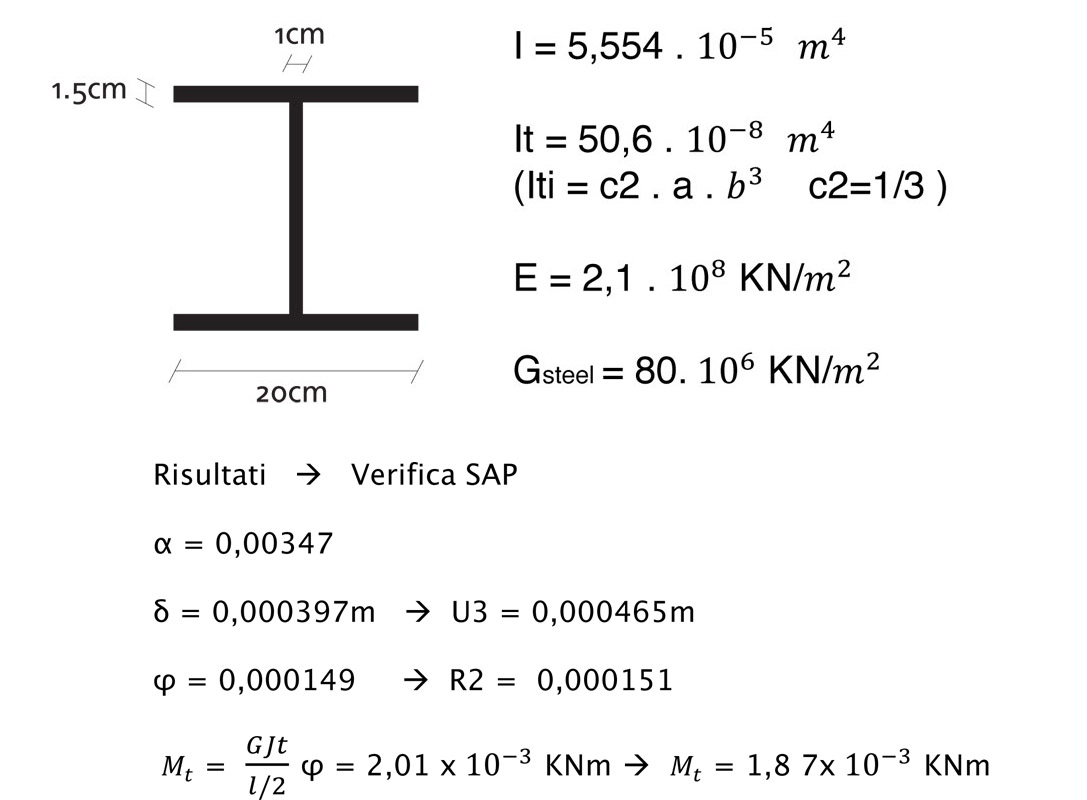
Ora l'obbiettivo è di capire in che modo la geometria delle sezioni ed il loro materiale influiscono sulla resistenza a torsione. Per fare ciò, prendiamo in esame quattro sezioni, due in acciaio (ipe, prof. scatolare) e due in cls (rettangolare e circolare), e confronteremo le loro restistenze (per facilitare la valutazione, le sezioni dello stesso manteriale hanno anche la stessa area).

Inizieremo mostrando i valori dei calcoli a mano per poi verificarli con SAP.

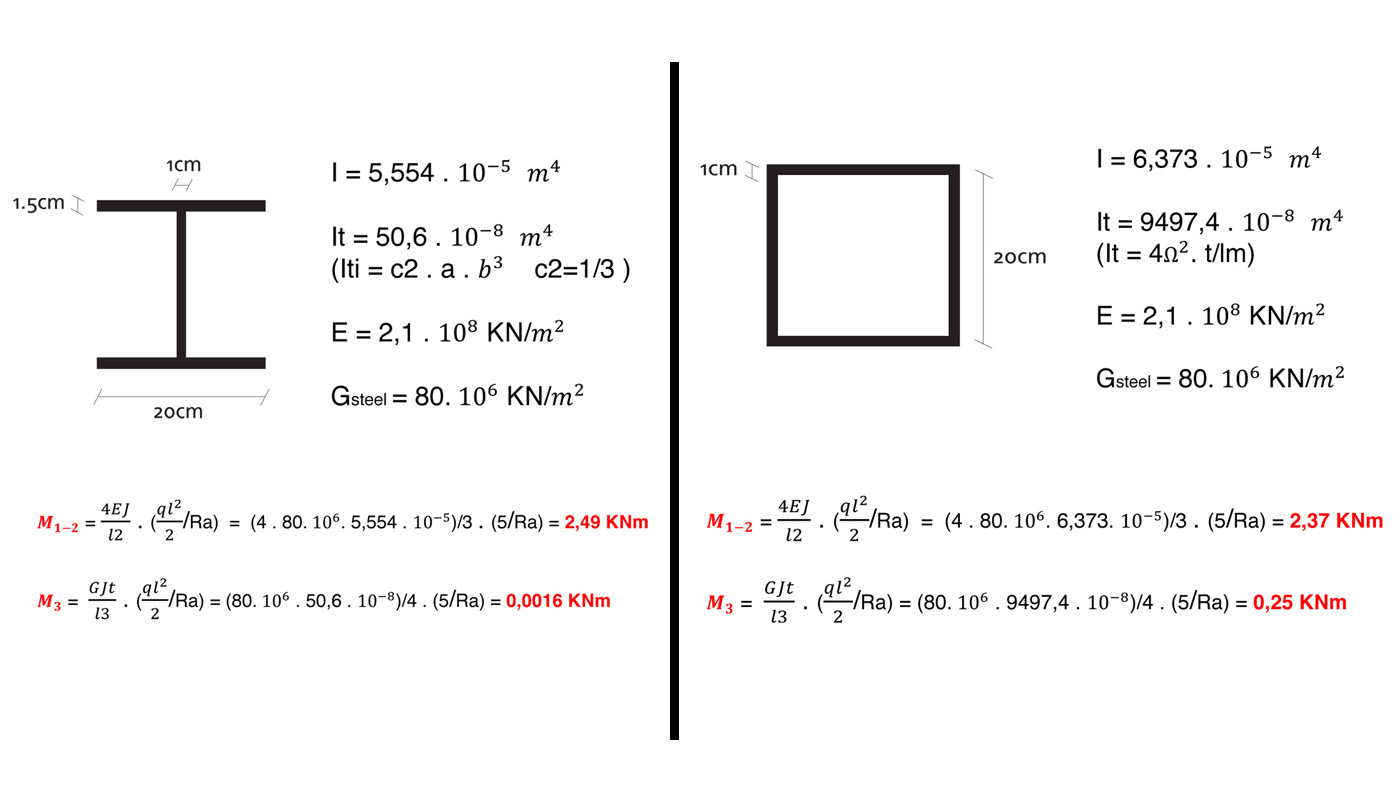
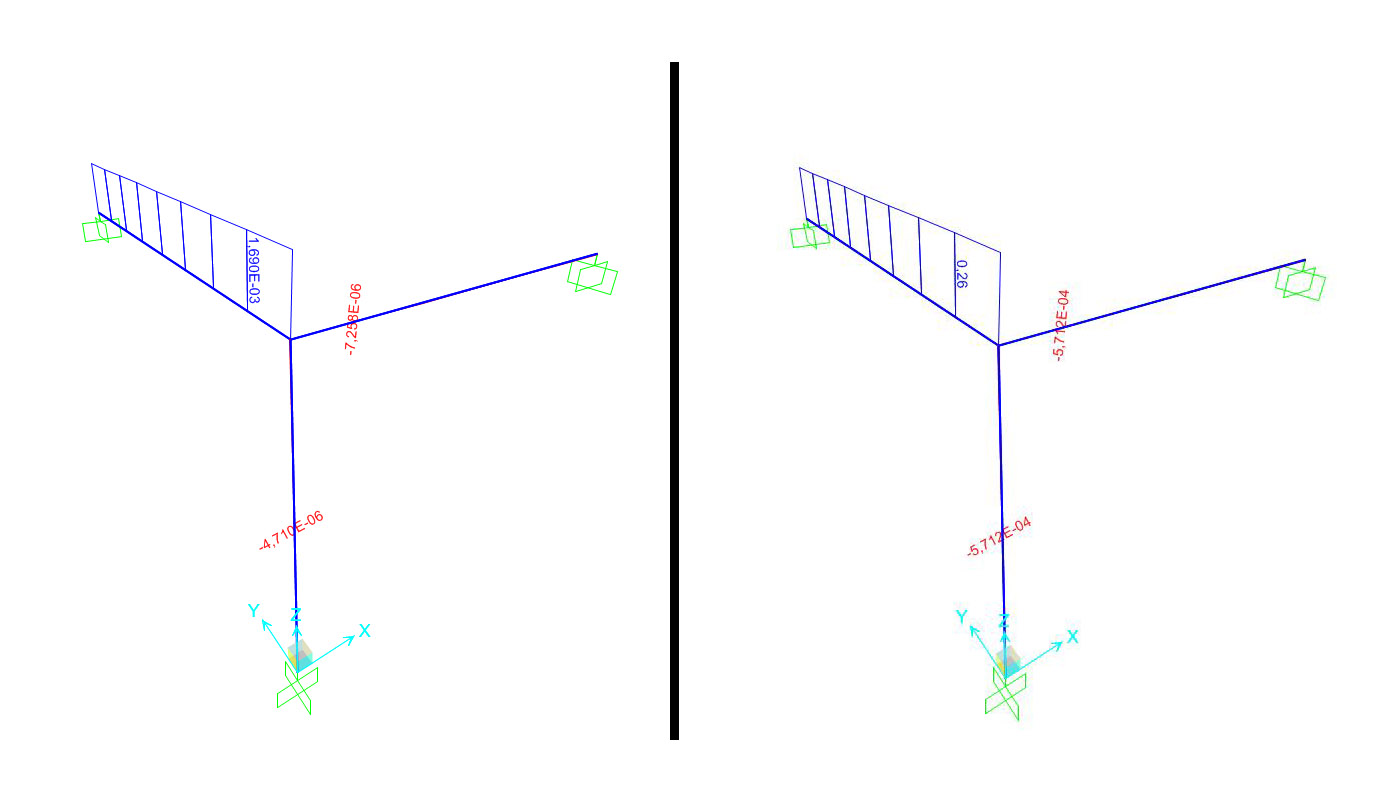
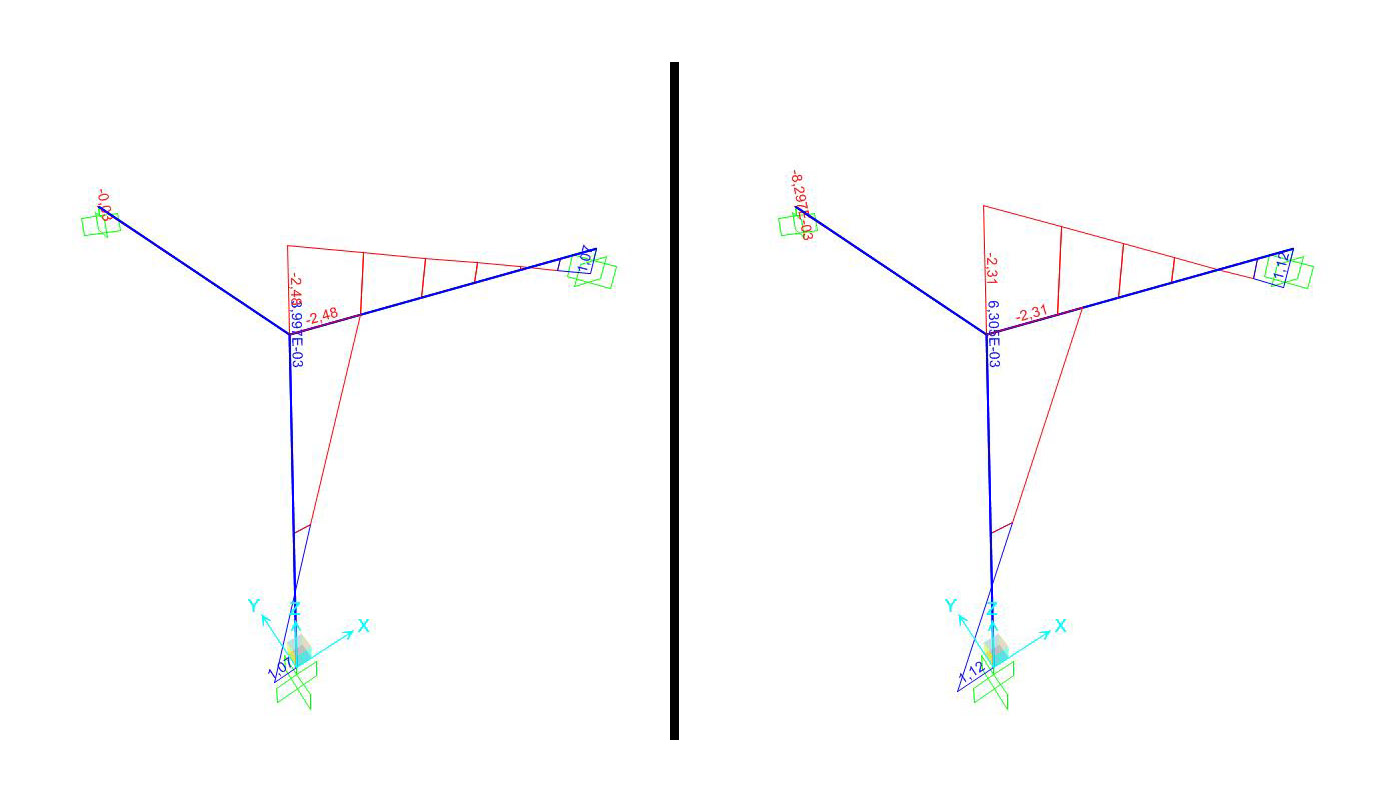
NB: oltre che con SAP possiamo verificare i risultati sommando i tre momenti, il risultato dovrà essere uguale a ql^2/2 (5KNm). Facendo ciò ho capito che le sezioni meno resistenti a torsione "obbligano" le aste inflesse a prendersi maggiore carico, tutto questo per un equilibrio più precario.

Esercizio 2:

In questo esercizio analizzeremo il comportamento di una struttura a graticcio di travi, ossia n intreccio di travi identiche ed ortogonali fra loro che, senza alcuna gerarchia collaborano per resistere ai carichi. Questo tipo di struttura può distinguersi tramite due particolarità: le travi essendo uguali devono avere tutte lo stesso momento d'inerzia e sopratutto devono avere il nodo ad incastro per trasmettere anche il momento.

Nel nostro caso studieremo la reazione di un graticcio semplice composto da due aste perpendicolari. Una di queste aste, essendo incastrata ad un terzo della sua lunghezza, provochera una rotazione che a sua volta genererà una torsione, tensione caratteristica di queste strutture.

Ogni corpo può traslare e ruotare in tre dimensioni, può dunque avere dodici gradi di libertà. Analizzando il nodo, sappiamo che non può ne traslare lungo x che lungo y dato che consideriamo le aste assialmente indeformabili, inoltre sappiamo che il nodo subisce una sola rotazione lungo l'asse y.

Le nostre variabili sono dunque due, lo spostamento lungo z e la rotazione lungo y.

Di seguito riportiamo gli "schemi noti" che torneranno utili per le varie equazioni di equilibrio:

A questo punto possiamo risolvere il problema grazie al metodo della sovrapposizione degli effetti:

Azione dovute all'abbassamento:

Azioni dovute alla rotazione del nodo:

I due equilibri (traslazione verticale e rotazione)

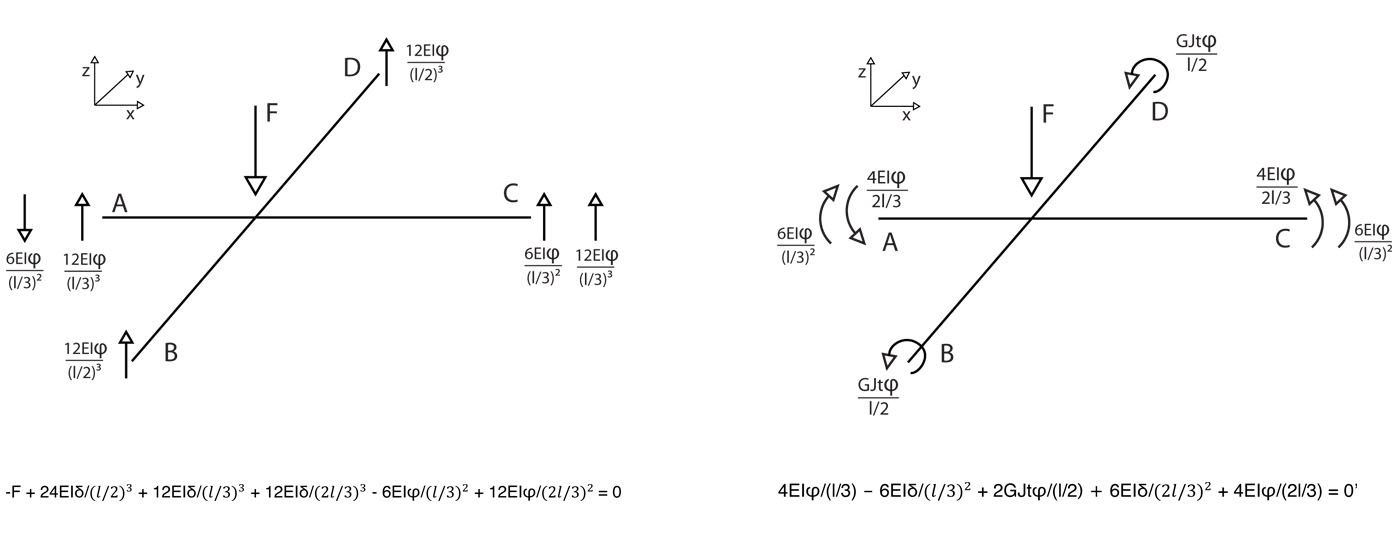
Ora possiamo sclegliere sezioni e materiali per confrontare i risultati.