ESERCITAZIONE_dimensionamento di un solaio in legno

Dimensionamento di un solaio ligneo

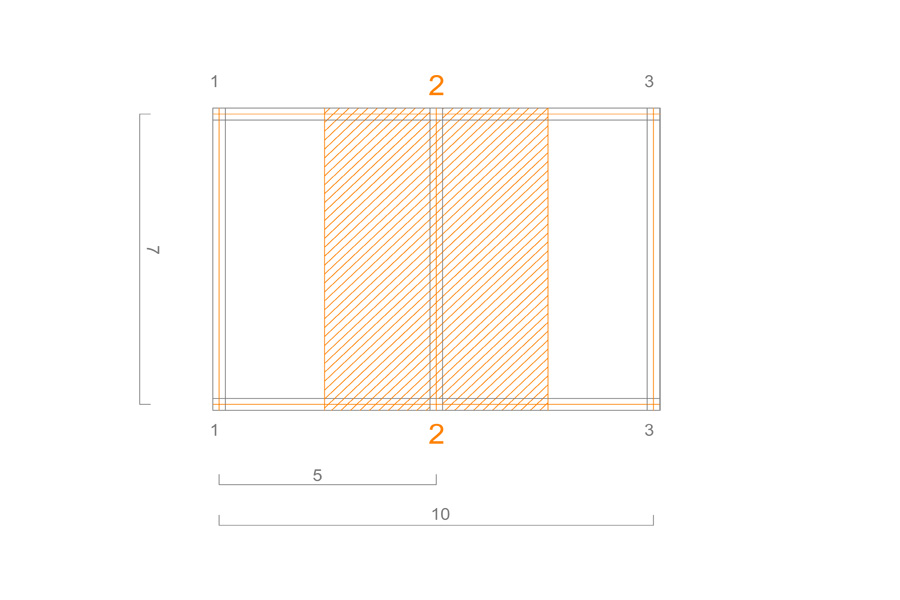
Si vuole dimensionare una trave di un solaio ligneo costituito da due campate di dimensioni 5X7 metri ciascuna.

Disegnamo quindi la struttura in pianta, e vediamo che la trave più sollecitata risulta essere la trave n.2, perchè la sua area di influenza è maggiore rispetto a quella delle altre due.

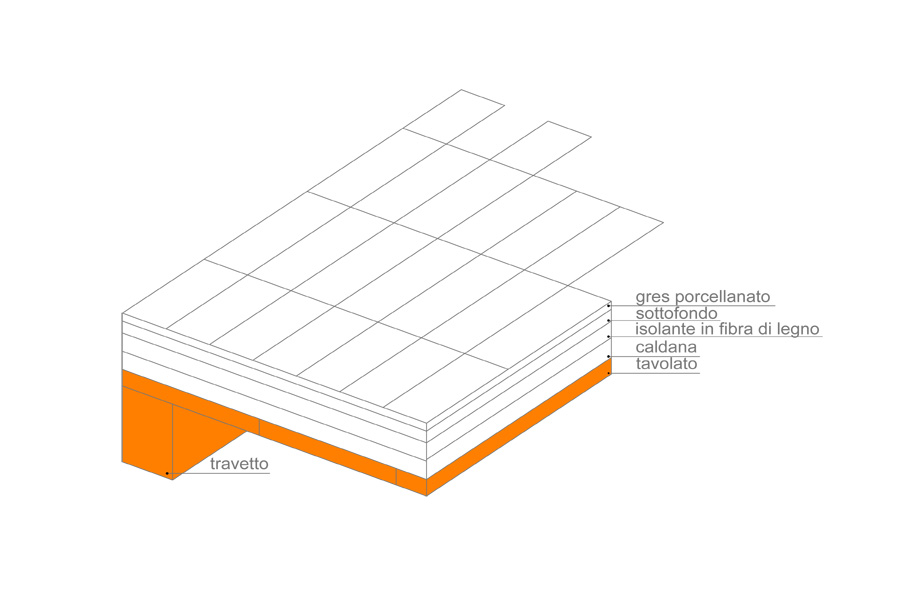
Consideriamo il solaio costituito dai seguenti elementi, con peso specific “P” e spessore “s” indicati:

pavimento in gres: P= 0,2 KN/mq; s=1,5 cm.

sottofondo: P=0,54 KN/mq; s=3 cm.

isolantein fibra di legno: P=0,0072 KN/mq; s=4 cm.

caldana: P=0,28 KN/mq; s=4cm.

tavolato: P=0,21 KN/mq; s=3 cm.

travetti: P=5 KN/mc; s=25 cm

Ci sono tre tipi diversi di carico che le travi del solaio devono sopportare:

Carichi strutturali “qs”, che sono quelli degli elementi strutturali

Carichi permanenti non strutturali “qp”.

Carichi accidentali “qa”, che per edifici residenziali è stimato pari a 2 KN/mq.

Procediamo così con i calcoli per determinare i vari carichi agenti considerando un’area pari a ad 1mq:

qs:

-travetti in legno (10X25 cm)

6KN/mc*1m*1m*0,25m=1,5 KN/mq

-tavolato:

0,21KN/mq*1m*1m*0,035m=0,00735 KN/mq

qp:

-caldana:

0,28 KN/mq*1m*1m*0,04m=0,011 KN/mq

-isolante in fibra di legno:

0,0072KN/mq*1m*1m*0,04m=0,00029KN /mq

-sottofondo:

0,54 KN/mq*1m*1m*0,03m=0,016 KN/mq

-pavimento in gres porcellanato:

0,2 KN/mq*1m*1m*0,01m=0,002 KN/mq

-incidenza degli impianti:

0,50 KN/mq.

qa:

2,00 KN/mq

calcolo  i carichi totali moltiplicandoli ognuno per il proprio coefficienti di sicurezza

qsTOT = 1,49 KN/mq

qpTOT= 0,04 KN/mq

qaTOT= 3 KN/mq

Ora si utilizza il foglio excel per poter determinare il valore del momento e scrivendo altri valori come il Kmod(= coefficiente di degrado nel tempo, che dipende dal carico e dall’umidità), e la resistenza caratteristica a flessione fmk pari a 24 N/mm^2 nel legno di classe GL24c.

La resistenza di progetto fd dovrà quindi essere pari alla σ ammissibile:

                                            σ ammissibile=fd

e sapendo che:

                                         fd=kmod*fmk/γm                                                   

completiamo la tabella inserendo i dati richiesti e troviamo la  e l’altezza della trave data una base che si ipotizza di 35 cm di spessore:

  Troviamo così che l’altezza necessaria della trave è 35,86 cm.