RIGIDEZZA TORSIONALE. Esercitazione con SAP2000

Turning Torso - Santiago Calatrava

Quando nel 2005 venne completato l'acclamato Turning Torso a Malmö, i sogni del committente (tale Johnny Örbäck, allora presidente della cooperativa HSB) divenivano finalmente realtà. Il nuovo quartiere super sostenibile e ultra accessorriato della piccola cittadina svedese aveva così un landmark adeguato, una moderna torre di Babele che celebrava l'egemonia della cooperativa nell'ambito dell'edilizia residenziale, la cui straniante invasività trovava lecita giustificazione grazie al diktat della progettazione sostenibile.

Di qualità architettonica discutibile, la peculiarità della torre che a noi interessa in questa sede è il suo dinamismo, generato da una virtuale torsione dell'edificio su sè stesso. L'immagine ci rende quindi facilmente intuibile in cosa consiste in realtà la deformazione dovuta a torsione, generata dall'azione di un momento torcente attorno all'asse longitudinale dell'oggetto. Man mano che ci allontaniamo dalla prima sezione incastrata dell'elemento in esame, tanto più le sezioni successive saranno deformate dalla forza torcente, come rappresentato dall'immagine:

Pertanto, nella progettazione del telaio di un edificio, il cui comportamento è sempre sistemico, è importante tenere presente che i momenti flettenti agenti su una trave forniscono ulteriori sollecitazioni alle travi perpendicolari ad essa, sottoforma di momenti torcenti. In questa esercitazione analizzeremo quindi, tramite SAP2000, le diverse rigidezze torsionali di alcuni profilati di acciaio e di alcune sezioni in calcestruzzo armato, tutti sottoposti alle stesse sollecitazioni. Utilizzeremo questo semplice schema strutturale:

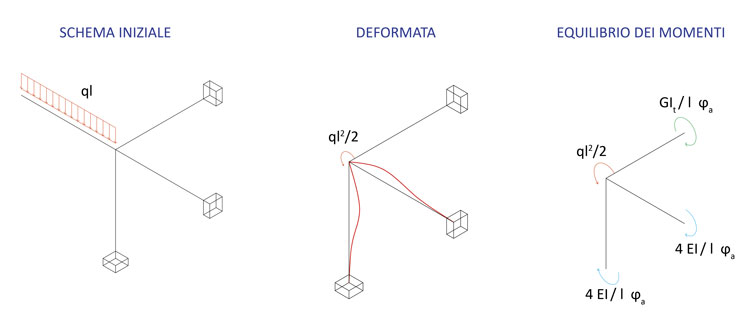
Eliminiamo la trave a sbalzo dello schema iniziale e la sostituiamo applicando al nodo un momento pari a ql²/2. Non è necessario aggiungere sul nodo anche la risultante del carico ql, in quanto, per l'elevata rigidezza del pilastro, la deformabilità assiale è trascurabile. Dagli schemi notevoli, inoltre, sappiamo quali momenti flettenti e torsionali si svilupperanno all'interno delle travi per bilanciare il momento generato dal carico agente sulla mensola. L'equazione di equilibrio alla rotazione sarà pertanto:

ql²/2 = ϕ_a ( 4EI/l + 4EI/l + GIT/l)

dove ϕ_a è la rotazione del nodo di cui vogliamo conoscere il valore. Dalla formula deduciamo che essa sarà in funzione dei soliti coefficienti E (modulo elastico), I (momento di inerzia), l (luce della trave) e di un nuovo coefficiente G, che indica il modulo di elasticità tangenziale, il cui valore cambia a seconda del materiale adottato.

Una volta fissati questi concetti, possiamo cominciare a impostare il nostro modello su SAP:

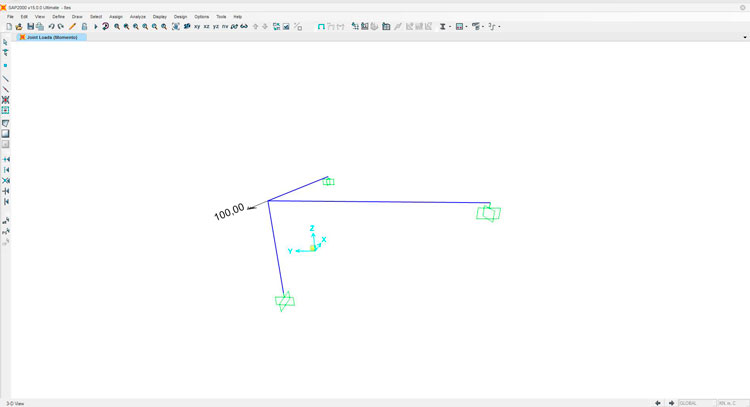
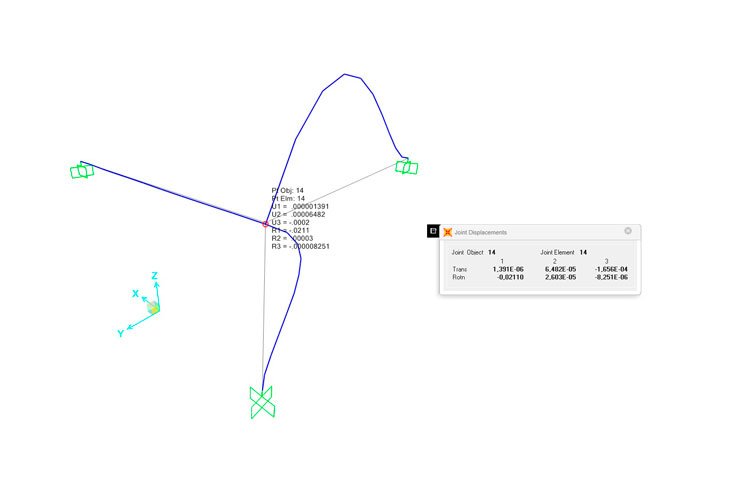
La deformata è stata intenzionalmente accentuata per mettere in evidenza la rotazione effettiva del nodo lungo l'asse x (R1). Di seguito i diagrammi delle sollecitazioni:

Taglio

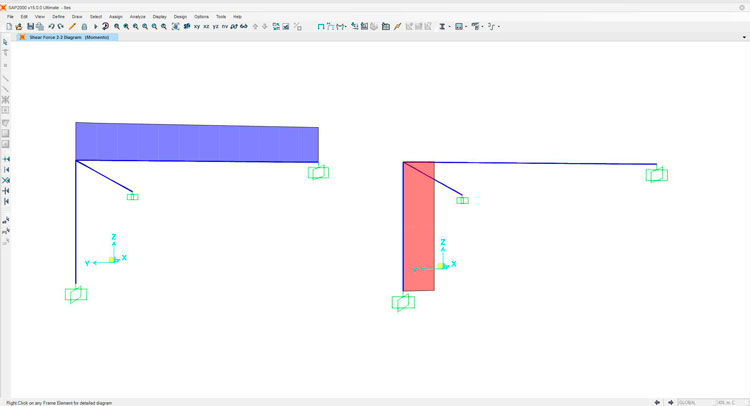
Momento

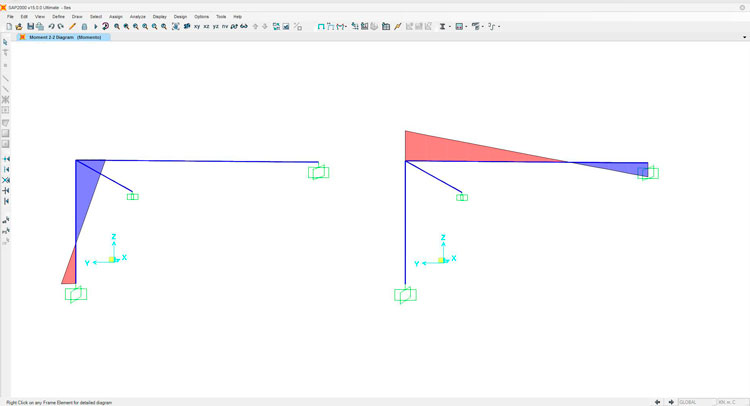
Torsione

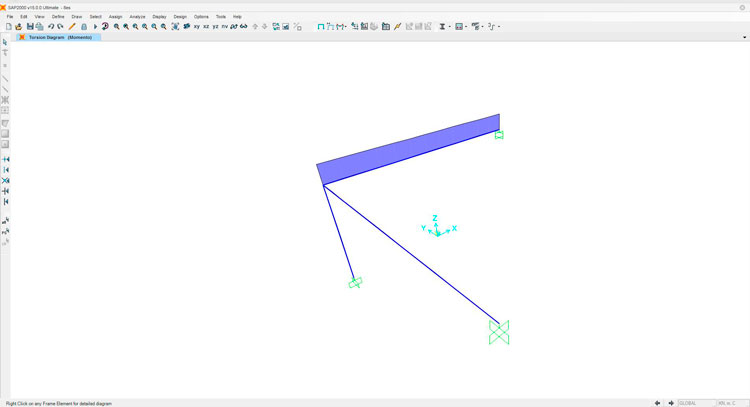
Stabilito il comportamento meccanico con delle sezioni generiche, passiamo ora ad utilizzare profili diversi per l'asta soggetta a torsione, annotando di volta in volta come cambia il valore della rotazione ϕ_a  del nodo, in base al profilato e al materiale utilizzato. Iniziamo con l'acciaio:

Profilo IPE

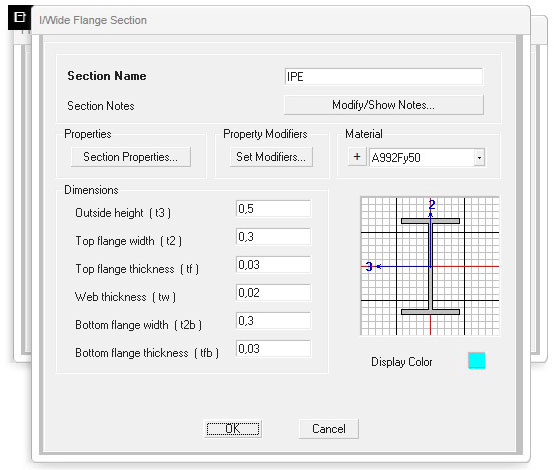
Profilo tubolare

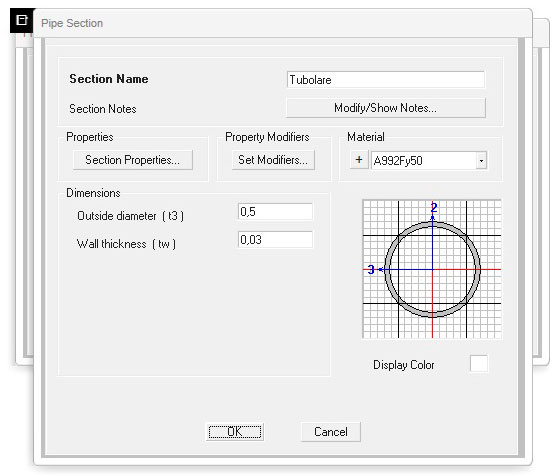
Profilo UPN

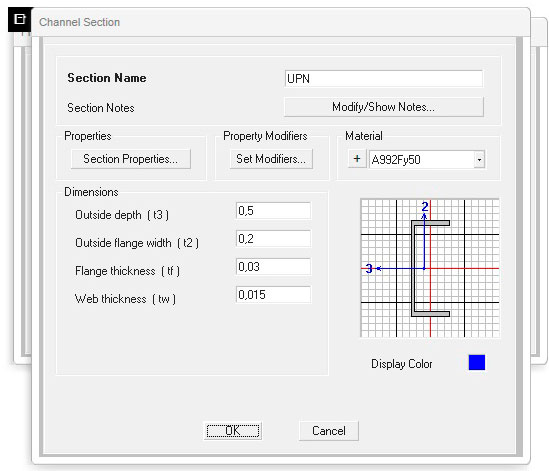
Sezione in CLS rettangolare

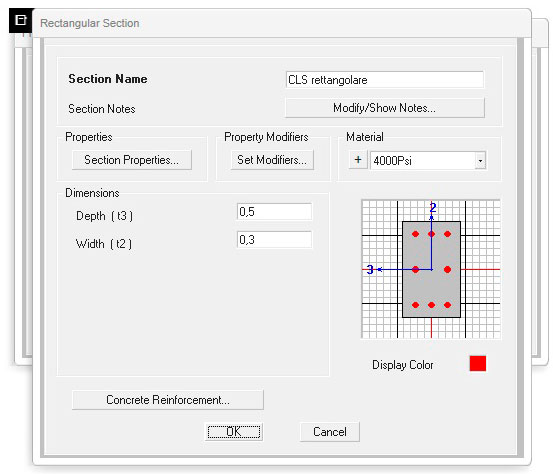
Sezione in CLS prefabbricato

Di seguito riportiamo una tabella che riassume i dati ottenuti:

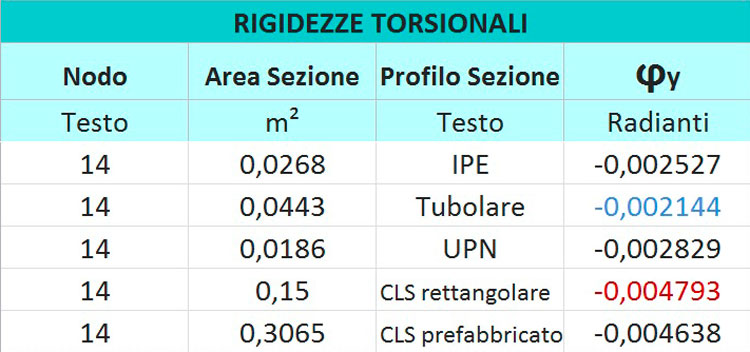
Alla luce di quanto ottenuto, possiamo quindi concludere che:

- L'acciaio, grazie ad un modulo di elasticità tangenziale (G) molto più alto del calcestruzzo, è decisamente il più performante dei materiali per quanto riguarda la torsione, nonostante l'area delle sezioni utilizzate sia di gran lunga inferiore.

- Tra i 3 profili in acciaio utilizzati, quello con la migliore rigidezza torsionale si è rivelato essere il profilo tubolare cavo, in quanto le tensioni tangenziali aumentano all'aumentare della loro distanza dall'asse torsionale. Avendo il profilo tubolare, per sua conformazione geometrica, una distanza media dall'asse risulta quindi essere la migliore soluzione.

- Le sezioni aperte invece costituiscono la peggiore scelta delle 3 in acciaio, ma comunque risultano essere sempre decisamente più rigide rispetto a delle sezioni in calcestruzzo piene, nonostante le sezioni piena siano avvantaggiate da un valore di I_t più alto.