blog di Hadi.Mounajed

Vestibolo d'antico tempio - Giovanbattista Piranesi

Nell'immaginario collettivo, quando si parla della monumentalità dell'architettura romana, si manifesta immediatamente l'immagine dell'ormai dimenticato arco. Nonostante esso sia già riscontrabile in età molto antica presso popoli culturalmente molto differenti (vd. Egitto 3500 a.C.), divenne celebre durante la fase repubblicana di Roma, grazie all'uso massivo che se ne fece, adottando generalmente l'arco a tutto sesto poggiato su pilastri. Con l'avvento del Cristianesimo, la cui architettura è mutuata da quella classica, l'arco continuò a dominare la scena architettonica, raggiungendo forse la sua catarsi nel Medioevo, in funzione di più complesse esigenze statico-costruttive, che portarono all'implementazione di nuovi tipi (archi acuti, lobati, ecc.). La cultura occidentale, dal Rinascimento al sec. XIX, ne ripropose invece i tipi e gli usi desunti dallo studio degli esempi romani. Il Movimento Moderno, dall'alto della sua arrogante necessità di fare tabula rasa, cancellò dal suo lessico l'arco, che fu relegato ad un malinconico ruolo di comprimario eccellente.

Dal punto di vista del comportamento statico, gli archi possono distinguersi in: incastrati, a due cerniere, a tre cerniere o a spinta eliminata. L'arco incastrato, tre volte iperstatico, è molto rigido ed è difficilmente soggetto a spostamenti eccessivi sotto carico,ma la sua analisi può risultare molto complessa. Il vantaggio della maggiore resistenza degli archi molto rigidi viene però controbilanciato dai problemi che proprio la loro rigidezza crea (specie se la luce è considerevole), allorquando nascano tensioni interne di origine termica o dovute a deformazioni lente nel tempo. Diminuendo la rigidezza si passa all'arcoa due cerniere, il quale, appunto perché più deformabile, mantiene tali tensioni entro limiti accettabili, per giungere all'arcoa tre cerniere isostatico, altamente deformabile, ma che permette di calcolare con precisione le spinte orizzontali e le forze interne (vd. Galerie des Machines). Gli archia spinta eliminata, infine, possono considerarsi archi a due cerniere nei quali l'incognita iperstatica è costituita dalla tensione della catena, che ne collega le imposte per assorbirne quella spinta che altrimenti sarebbe destinata ai piedritti.

In questa ultima esercitazione ci limiteremo ad analizzare gli archi a tre cerniere isostatici, sia dal punto di vista teorico che da quello pratico, verificando il loro comportamento meccanico su SAP2000. Iniziamo col sottolineare che gli archi fanno parte di quegli elementi architettonici che resistono per forma, lavorano a compressione e possono essere in alcuni casi (vd. arco parabolico) strutture altamente ottimizzate, ovvero in grado di assorbire i carichi e di trasformarli in sforzo normale. Ciò ovviamente andrà a discapito della riserva di resistenza, utile, ad esempio, nel caso del sisma. Questa attitudine degli archi a trasformare tutto il carico in sforzo normale, ignorando la flessione, si chiama architudine.

 

ARCO A TUTTO SESTO a 3 cerniere

San Lorenzo fuori le mura - Roma

Trattiamo innanzitutto l'arco a tutto sesto a tre cerniere. Esso è sostanzialemente definito da una semicirconferenza e può essere considerato alla stregua del portale a 3 cerniere, in quanto è caratterizzato dalle stesse reazioni vincolari:

Considerando la simmetria della struttura, le reazioni vincolari sono facilmente ricavabili dall'equazione di equilibrio alla rotazione, in quanto, non essendoci taglio in chiave, il carico verrà contrastato dalla reazione verticale all'imposta:

Una volta trovate le reazioni vincolari, si passa allo studio delle azioni di contatto all'interno di una sezione generica dell'arco. Per fare ciò è necessario adottare il metodo delle parti, utilizzando qualsivoglia sezione contenuta all'interno dell'intervallo definito da 0<α<90:

Nelle azioni di contatto subentreranno quindi semplici nozioni di trigonometria, che ci permettono di scomporre le risultanti inclinate nelle canoniche forze orizzontali o verticali, cosicchè sia possibile procedere alla scrittura delle equazioni di equilibrio (con polo in B):

Come si nota nelle prime 2 equazioni N e T sono accoppiati (e lo sarebbero stati anche nella 3° se non avessimo preso il polo in B), caratteristica essenziale delle strutture curve. Se provassimo a prendere ad esempio un arco a tutto sesto di raggio e freccia pari ad l sottoposto ad un carico distribuito pari a 10 KN/m, avremmo i seguenti risultati:

Gli sforzi assiali varieranno da -80KN all'imposta a -40 KN in chiave, quelli di taglio da 40 KN all'imposta a 0 KN in chiave e i momenti flettenti saranno ovviamente 0 KNm agli estremi fino a raggiungere un picco di -80 KNm all'interno della sezione dell'arco. Confronteremo successivamente questi risultati con la seguente tipologia di arco.

Nel frattempo portiamo su SAP2000 l'arco a tutto sesto per verificare se quanto detto finora sia valido. Modelliamo il nostro arco su AUTOCAD, disegnando una circonferenza di 5 m di raggio e tagliandone solo la metà che ci occorre. Spezziamo il nostro arco in corrispondenza della chiave di volta e ruotiamolo in 3D affinchè la sua freccia sia orientata secondo il piano z. Dopo aver salvato in dxf 2004 lo importo su SAP2000:

Assegno 2 cerniere alle imposte dell'arco e col solito comando (ASSIGN - FRAME - RELEASE/PARTIAL FIXITY spuntando la casella del momento M 3-3) assegno il rilascio in chiave:

Assegno delle sezioni di calcestruzzo con lato maggiore uscente dal piano di dimensione 0,25m x 0,50m:

Assegno un carico distribuito di 10 KN/m, avendo la premura di scegliere come opzione GRAVITY PROJECTED, in modo tale che venga spalmato sull'orizzontale dell'arco. Rimuovo inoltre il peso proprio della struttura:

Faccio partire l'analisi:

Deformata

Sforzo normale

Taglio

Momento flettente

Reazioni vincolari:

I dati di SAP2000 non fanno che confermare quanto detto sopra. Sotto la spinta del carico, l'arco tende a spanciare lateralmente e viene riportato al suo posto dall'azione dei vincoli alle imposte. I valori dello sforzo normale tendono a diminuire man mano che si va dall'imposta alla chiave, per poi effettuare il processo inverso. I momenti sono ovviamente 0 in corrispondenza delle cerniere e massimi nelle parti mediali dei due semi-archi. Ci annotiamo inoltre i valori max delle sollecitazioni per metterli a confronto dopo con l'arco ribassato: Nmax = 50KN; Tmax = 23,65 KN; Mmax = 31,16 KNm.

 

ARCO CIRCOLARE RIBASSATO a 3 cerniere

Ponte degli Annibaldi - Insula

Come suggerisce il nome, l'arco circolare ribassato è costruito sempre a partire dalla circonferenza, di cui però sfrutta non più l'esatta metà, bensì un intervallo più piccolo, tale che f < l. Trattandosi comunque di un arco a 3 cerniere, le sue reazioni vincolari saranno sempre le stesse:

A differenza della precedente tipologia più immediata, in questo caso la prima cosa da fare è trovare l'angolo α₀ che rispetto al centro della circonferenza individua la sezione di imposta:

Grazie al teorema di Pitagora ricaviamo il valore della retta R che collega il centro dell'ipotetica circonferenza con la sezione d'imposta dell'arco. Visto che l'arco da 0 ad α₀ non esiste, introduciamo un secondo angolo α e procediamo come prima grazie al metodo delle parti:

Con la scomposizione delle azioni di contatto N(α) e T(α) nelle loro componenti elementari e dopo aver trovato il valore di ogni braccio, possiamo scrivere le equazioni di equilibrio (con polo in S):

 

Se proviamo ad applicare i valori dell'esempio precedente all'arco ribassato, curandoci di portare la freccia da 8m a 4 m, avremmo i seguenti risultati (con α₀=0,64 rad) :

Notiamo subito che la spinta dell'arco è raddoppiata rispetto all'arco a tutto sesto, mentre consultando un apposito tabellario sappiamo che gli sforzi assiali raggiungono valori di 115 KN, gli sforzi di taglio 15 KN e i momenti flettenti 20 KNm (vedi immagine). Possiamo quindi concludere che lo sforzo normale è decisamente incrementato, mentre il taglio risulta essere meno della metà e il momento flettente addirittura 4 volte inferiore.

Vediamo ora su SAP2000 se le nostre conclusioni vengono confermate. Disegnamo su AUTOCAD un arco di circonferenza con raggio 5m e freccia di 2,5m e lo importiamo su SAP2000 come fatto in precedenza, assegnando poi i vincoli, il rilascio in chiave, le sezioni in calcestruzzo ed il carico distribuito:

Deformata

Sforzo normale

Taglio

Momento flettente

Reazioni vincolari

Le riflessioni fatte in precedenza rimangono valide anche per questo modello di arco, ma balza subito all'occhio come la spinta dell'arco all'imposta sia il doppio dell'arco a tutto sesto. Inoltre analizzando i valori massimi delle sollecitazioni abbiamo ottenuto i seguenti valori: Nmax = 70,25 KN; Tmax = 9,40 KN; Mmax = 7,8 KNm.
Lo sforzo normale è sensibilmente aumentato, mentre il taglio è inferiore alla metà e il momento flettente addirittura 4 volte inferiore al precedente.

 

ARCO PARABOLICO a 3 cerniere

Miho Museum - Arco parabolico d'ingresso

L'arco parabolico isostatico, a differenza dei due precedenti, è una struttura perfettamente ottimizzata. La sua capacità, come detto in precedenza, consiste nel trasformare la densità di carico ripartita uniformemente sull'orizzontale in sforzo normale puro, all'interno di ogni singola sezione. Si dice quindi che l'arco parabolico isostatico è funicolare rispetto al carico ripartito. Non essendo più in presenza di una struttura definita dalla funzione circonferenza, per dimostrare che effettivamente l'unica tensione interna diversa da 0 è lo sforzo normale, dobbiamo innanzitutto analizzare l'equazione della parabola:

La famiglia di parabole che descrive il nostro arco è:

y = ax² + bx + c 

Imponiamo l'appartenenza dei punti A,B,C alla parabola e troviamo l'equazione esatta che descrive la nostra parabola:

A ► x=0; y=0; -> c = 0
B ► x=l; y=f; ->  al² + bl² + c = f
C ► x=2l; y=0; ->  4al² + 2bl + c = 0

Mettiamo le 3 equazioni a sistema e otterremo che:

a = - f/l²           b = 2 f/l               c = 0

L'equazione sarà quindi:

Dato che siamo in presenza di una struttura curva più complessa delle precedenti e non potendo utilizzare l'angolo α come prima, ci calcoliamo la tangente alla parabola tramite la derivata, cosicchè sia possibile scomporre le azioni di contatto dopo aver applicato il metodo delle parti:

 

Dalla prima equazione ricaviamo:

Sostituendo nella seconda:

Sostituisco a tanβ il valore precedentemente ricavato:

 

Vediamo ora il momento flettente:

 

Come anticipato quindi, essendo M(x) e T(x) nulli, l'arco parabolico costringe il materiale a lavorare solo a compressione, risultando così come una struttura altamente ottimizzata.Vediamo in ultimo come si comporta l'arco parabolico su SAP2000. Lo modelliamo su AUTOCAD tramite il comando spline, spezzandolo come usuale in chiave, e avendo la premura di trasformare la spline in polilinea (con una precisione >5) e di esplodere il tutto prima di salvare. Questo è quello che si ottiene importandolo su SAP2000:

Assegno di nuovo i vincoli alla base, il rilascio in chiave, le sezioni di calcestruzzo ed il carico distribuito:

Deformata

Sforzo normale

Nel caso in cui il taglio e il momento non siano pari a 0, basterà reimportare l'arco su SAP2000 dopo aver convertito la spline in polilinea con una precisione più alta.

 

In questo breve post pubblico la prima esercitazione, che, a causa di un fraintendimento, non si trova collocata assieme a quella sulle travi reticolari piane. Tratteremo in questo ambito sempre di travi reticolari, ma in questo caso non più giacenti su un piano bidimensionale, bensì nell'intero dominio tridimensionale dello spazio. Proprio per questa loro caratteristica, esse ben si prefigurano a resistere alle sollecitazioni agenti su tutti e tre gli assi cartesiani e, se ben progettate, grazie alla prefabbricazione ed alla standardizzazione degli elementi costitutivi, il costo della loro opera risulta diminuito, i lavori in cantiere sono semplificati e terminati più rapidamente. Morfologicamente esse si presentano come una consistente quantità di aste collegate tra loro in modo da formare un grigliato. Grazie a questa disposizione, i carichi isolati agenti in alcuni punti dell'opera non sono sopportatati soltanto dagli elementi direttamente caricati, ma anche da altri che si trovano a notevole distanza dai carichi stessi. Le considerevoli tensioni negli elementi direttamente caricati diminuiscono, mentre aumentano quelle negli altri elementi, così da ottenere una distribuzione più omogenea delle sollecitazioni nell'insieme della struttura. Nella maggior parte dei casi, come riportato in foto, il nodo tra le aste è costituito da una cerniera 3D, che permette la rotazione lungo i tre assi.

Vediamo quindi come disegnare un tale sistema con SAP2000. Iniziamo innanzitutto modellando su AUTOCAD una maglia sul piano xy, costituita da linee singole (non polilinee) di lunghezza 2 m di lato, a formare un quadrato con 2 vertici collegati da una diagonale:

Dobbiamo ora completare lo schema anche sul piano z, ricordandoci di evitare che alcune linee si sovrappongano o siano assegnate al layer 0:

 

Una volta salvato il file di AUTOCAD in .dxf, possiamo importarlo in SAP2000:

 

 

 

Scegliamo l’acciaio come materiale delle aste, assegnandogli una sezione tubolare (pipe), tramite il comando DEFINE > SECTION PROPERTIES > FRAME SECTIONS:

Assegniamo ora i carichi, applicandoli su tutti i nodi superiori della travatura reticolare, come il modello di queste travi ci impone. E' opportuno inoltre, prima di avviare l’analisi, scaricare ogni asta dal peso proprio della struttura, in quanto costituirebbe un carico distribuito su aste il cui modello ci obbliga a considerare scariche. Creiamo quindi un nuovo LOAD PATTERN che abbia 0 come coefficiente di moltiplicazione del carico SELF WEIGHT MULTIPLER:

 

Dato che in una struttura reticolare le aste hanno come vincoli interni delle cerniere, occorre eseguire un’operazione di rilascio del momento, tramite il comando ASSIGN > FRAME > RELEASE > MOMENT 3-3(MAJOR) > START 0 – END 0:

Avviando al solito modo l'analisi, ci verrà restituita sullo schermo la deformata e, cliccando su SHOW FORCES/STRESSES > FRAME/CABLES > AXIAL FORCE, anche il diagramma degli sforzi assiali delle aste, unici sforzi reagenti della struttura:

 

Non ci rimane che quantificare a quali tensioni sia soggetta ogni asta, tramite l'apposito tasto di tabellazione dei valori, apponendo sul menù che si apre la spunta alla casella ELEMENT FORCES - FRAMES:

Esportiamo la tabella ottenuta su Excel, riportando come valori solo quello dello sforzo normale (N), dell'area e delle tensioni σ  = (N/A) di ogni asta, in funzione delle quali si sceglierà opportunamente l'acciaio da usare. In particolare si noti come i valori negativi indichino le aste compresse (puntoni), mentre quelli positivi le aste tirate (tiranti).

Padiglione della Fiera di Rimini - GMP Architekten

Dopo aver iniziato a trattare la torsione nel precedente post, vediamo in questo caso quali sono le implicazioni di tale tensione su un sistema più complesso, quale il graticcio. Gli impalcati a graticcio sono costituiti da un numero variabile di travi longitudinali, fra loro affiancate e collegate puntualmente da elementi irrigidenti trasversali, detti traversi. Le travi principali, poste ad interasse i, ed i traversi, posti ad interasse j, formano una maglia generalmente rettangolare pari a ixj. Dal punto di vista del comportamento strutturale, gli impalcati a graticcio hanno una minore rigidezza torsionale rispetto a quelli a cassone e rispetto le travi reticolari spaziali, ma sono sicuramente un giusto compromesso tra i sistemi a telaio ordinari e strutture più ardite, senza trascurare l'oggettiva e significativa istanza estetica di tali sistemi: è esemplificativa in merito la copertura dei padiglioni della Fiera di Rimini (vd. foto).

In questa esercitazione proveremo a risolvere manualmente uno stralcio dell'impalcato, verificando in seguito la bontà del procedimento eseguito tramite SAP2000. Lo schema in questione è il seguente:

 

Per la deformata e i valori di taglio e momento, ci riferiamo agli ormai celebri schemi notevoli della trave doppiamente incastrata:

In questo caso abbiamo però una complicazione. Le due travi del graticcio si intersecano ad 1/3 della trave AC, permettendo così alla forza applicata nel nodo di generare una rotazione ϕy. Il risultato della deformata nella trave AC sarà quindi uguale alla somma dell'abbassamento δ e della rotazione ϕy, mentre sulla trave BD agirà esclusivamente l'abbassamento, in virtù della curvatura χ=0 in corrispondenza del punto di applicazione della forza:
 

 
Ai fini dello svolgimento dell'esercizio sarà quindi opportuno separare l'azione dei due diversi effetti, per poi sovrapporli alla fine. Iniziamo dall'abbassamento δ sulla trave AC:

Passiamo ora all'abbassamento δ sulla trave BD:

Nel caso della trave BD, i momenti flettenti si annullano l'uno con l'altro e verranno quindi ignorati nella successiva equazione di equilibrio alla rotazione. Lasciamo agire ora solo la rotazione ϕy sulla trave AC, riferendoci agli schemi notevoli della rotazione su una trave doppiamente incastrata:

 

 

Come già spiegato in precedenza, la trave BD è esente da sollecitazioni rotazionali, ma sappiamo anche che la flessione sull'asse x provoca inevitabilmente la torsione sull'asse perpendicolare, su cui giace la trave in questione:

 

La trave reagirà quindi alla sollecitazione con un momento torcente di verso opposto alla rotazione ϕy.

Dopo aver esaminato tutti gli effetti separatamente, possiamo ora sovrapporli tra di loro, scrivendo prima l'equazione di equilibrio alla traslazione verticale e poi quella di equilibrio alla rotazione:

 

Abbiamo quindi un sistema di 2 equazioni in 2 incognite. Per non affrontare tutto il calcolo a mano si è scelto di adottare il software Mathematica 8, tramite il quale ricavare i valori delle incognite ϕy e δ:

Quindi:

                                          δ = 2Fl³/1113EI                                       ϕy = 9Fl²/742 (3EI+4I_t )

Non ci rimane che portare il nostro semplice graticcio su SAP2000, per vedere come varia l'abbassamento e la rotazione del nodo a cui è applicata la forza, in funzione della rigidezza del sistema intero, che ricordiamo essere la somma della rigidezza flessionale e della rigidezza torsionale. Iniziamo disegnando l'impalcato con delle sezioni generiche, e verificando la congruenza della deformata e dei diagrammi delle sollecitazioni:

Deformata:

Taglio:

Momento:

Lasciando sempre fissa la sezione della trave AC (IPE500), variamo la sezione della BD e riportiamo i valori dell'abbassamento e della rotazione del nodo d'intersezione su un'apposita tabella. Come sezioni di prova adotteremo una IPE500, una scatolare e una tubolare:

 

 

 

 

Come già dimostrato nella precedente esercitazione, i profili chiusi (ed in particolare i profili tubolari) offrono una maggiore rigidezza torsionale, che, inevitabilmente, comporta anche un minore abbassamento del nodo d'intersezione delle travi.

Turning Torso - Santiago Calatrava

Quando nel 2005 venne completato l'acclamato Turning Torso a Malmö, i sogni del committente (tale Johnny Örbäck, allora presidente della cooperativa HSB) divenivano finalmente realtà. Il nuovo quartiere super sostenibile e ultra accessorriato della piccola cittadina svedese aveva così un landmark adeguato, una moderna torre di Babele che celebrava l'egemonia della cooperativa nell'ambito dell'edilizia residenziale, la cui straniante invasività trovava lecita giustificazione grazie al diktat della progettazione sostenibile.

Di qualità architettonica discutibile, la peculiarità della torre che a noi interessa in questa sede è il suo dinamismo, generato da una virtuale torsione dell'edificio su sè stesso. L'immagine ci rende quindi facilmente intuibile in cosa consiste in realtà la deformazione dovuta a torsione, generata dall'azione di un momento torcente attorno all'asse longitudinale dell'oggetto. Man mano che ci allontaniamo dalla prima sezione incastrata dell'elemento in esame, tanto più le sezioni successive saranno deformate dalla forza torcente, come rappresentato dall'immagine:

Pertanto, nella progettazione del telaio di un edificio, il cui comportamento è sempre sistemico, è importante tenere presente che i momenti flettenti agenti su una trave forniscono ulteriori sollecitazioni alle travi perpendicolari ad essa, sottoforma di momenti torcenti. In questa esercitazione analizzeremo quindi, tramite SAP2000, le diverse rigidezze torsionali di alcuni profilati di acciaio e di alcune sezioni in calcestruzzo armato, tutti sottoposti alle stesse sollecitazioni. Utilizzeremo questo semplice schema strutturale:

Eliminiamo la trave a sbalzo dello schema iniziale e la sostituiamo applicando al nodo un momento pari a ql²/2. Non è necessario aggiungere sul nodo anche la risultante del carico ql, in quanto, per l'elevata rigidezza del pilastro, la deformabilità assiale è trascurabile. Dagli schemi notevoli, inoltre, sappiamo quali momenti flettenti e torsionali si svilupperanno all'interno delle travi per bilanciare il momento generato dal carico agente sulla mensola. L'equazione di equilibrio alla rotazione sarà pertanto:

ql²/2 = ϕ_a ( 4EI/l + 4EI/l + GIT/l)

dove ϕ_a è la rotazione del nodo di cui vogliamo conoscere il valore. Dalla formula deduciamo che essa sarà in funzione dei soliti coefficienti E (modulo elastico), I (momento di inerzia), l (luce della trave) e di un nuovo coefficiente G, che indica il modulo di elasticità tangenziale, il cui valore cambia a seconda del materiale adottato.

Una volta fissati questi concetti, possiamo cominciare a impostare il nostro modello su SAP:

La deformata è stata intenzionalmente accentuata per mettere in evidenza la rotazione effettiva del nodo lungo l'asse x (R1). Di seguito i diagrammi delle sollecitazioni:

Taglio

Momento

Torsione

Stabilito il comportamento meccanico con delle sezioni generiche, passiamo ora ad utilizzare profili diversi per l'asta soggetta a torsione, annotando di volta in volta come cambia il valore della rotazione ϕ_a  del nodo, in base al profilato e al materiale utilizzato. Iniziamo con l'acciaio:

Profilo IPE

Profilo tubolare

Profilo UPN

Sezione in CLS rettangolare

Sezione in CLS prefabbricato

 

Di seguito riportiamo una tabella che riassume i dati ottenuti:

Alla luce di quanto ottenuto, possiamo quindi concludere che:

- L'acciaio, grazie ad un modulo di elasticità tangenziale (G) molto più alto del calcestruzzo, è decisamente il più performante dei materiali per quanto riguarda la torsione, nonostante l'area delle sezioni utilizzate sia di gran lunga inferiore.

- Tra i 3 profili in acciaio utilizzati, quello con la migliore rigidezza torsionale si è rivelato essere il profilo tubolare cavo, in quanto le tensioni tangenziali aumentano all'aumentare della loro distanza dall'asse torsionale. Avendo il profilo tubolare, per sua conformazione geometrica, una distanza media dall'asse risulta quindi essere la migliore soluzione.

- Le sezioni aperte invece costituiscono la peggiore scelta delle 3 in acciaio, ma comunque risultano essere sempre decisamente più rigide rispetto a delle sezioni in calcestruzzo piene, nonostante le sezioni piena siano avvantaggiate da un valore di I_t più alto.

Edificio della Prefettura - L'Aquila

Era il 6 aprile 2009 alle ore 3:32 quando la città de L'Aquila e i paesi circostanti venivano colpiti da una scossa sismica dell'VIII grado della scala Mercalli. I danni furono ingenti, sia per le vittime che per la molteplicità di beni storici e artistici devastati. In molti, subito dopo la sciagura, si appellarono alla negligenza dei progettisti, i quali avevano deliberatamente ignorato il DM 2008, il quale prevede una serie di normative atte alla progettazione di impalcati idonei a resistere all'azione delle spinte orizzontali, quali appunto il sisma. Per questo, oggigiorno, risulta assolutamente indispensabile per un progettista avere un bagaglio di conoscenze che gli permettano di progettare un edificio, la cui struttura comprenda degli elementi irrigidenti finalizzati all'assorbimento delle spinte orizzontali. Tali elementi vengono chiamati controventi.

In questa esercitazione andremo quindi ad esaminare qual è l'azione di una forza orizzontale su di un impalcato così strutturato:

Dobbiamo innanzitutto fare due considerazioni:

- ipotizzando che il solaio sia un diaframma rigido, il suo comportamento meccanico sarà tale da poterlo equiparare a quello di un corpo rigido. Gli spostamenti che esso potrà compiere saranno, quindi, la traslazione orizzontale, la traslazione verticale e la rotazione;

- il comportamento meccanico dei telai invece è quello dei corpi elastici, che si deformano assorbendo il carico orizzontale come se fossero delle molle.

Giova inoltre sottolineare che, avendo i controventi delle rigidezze diverse, la struttura non trasla solamente, bensì, generandosi un braccio pari alla distanza del centro delle masse dal centro delle rigidezze, essa è soggetta anche a rotazione. Nel caso in cui il braccio fosse eccessivo, la struttura sarebbe soggetta ad un momento troppo grande che la porterebbe inevitabilmente al collasso.

Da notare, infine, che i pilastri dell'impalcato (30x40 cm) sono disposti secondo due orientamenti diversi e avranno quindi momenti d'inerzia diversi:

Ora, tramite un foglio di calcolo Excel, vediamo come si comporta il suddetto impalcato, quando è soggetto ad una forza orizzontale.

 

STEP 1: calcolo delle rigidezze traslanti dei controventi dell'edificio

Come primo passo, abbiamo calcolato la rigidezza traslante di ogni controvento costituente l'impalcato. A sinistra vi sono i telai paralleli l'asse y, mentre a destra lungo l'asse x. In tutto e due i casi la K_T risultante di ogni telaio deriva dalla formula:

che non è nient'altro che la formula del taglio in un corpo rigido, dove:

E = modulo di Young (21000 per il calcestruzzo)

ΣiJi = sommatoria dei momenti di inerzia di pilastri del telaio

h = altezza dei pilastri dell'impalcato

 

 

STEP 2: tabella sinottica controventi e distanze

 

 

In questa tabella riassuntiva sono semplicemente riportate le rigidezze calcolate precedentemente e le distanze dei controventi dal punto O.

 

STEP 3: calcolo del centro di massa

Una volta stabilite le rigidezze dei telai e le loro distanze dall’origine O, l’impalcato è stato suddiviso in tre aree:

A1= 60 m²               A2 = 36 m²                  A3 = 18 m²

delle quali sono stati calcolati i rispettivi centri di massa, semplicemente tracciando le diagonali di ogni rettangolo. Ottenute le coordinate relative, abbiamo calcolato il centro di massa dell’intera struttura tramite questa semplice formula:

X_G = (A₁ x_G1 + A₂ x_G2 + A₃ x_G3) / (A₁ + A₂ + A₃) = 5,18 m

 

Y_G = (A₁ y_G1 + A₂ y_G2 + A₃ y_G3) / (A₁ + A₂ + A₃) = 6,47 m

 

 

 

STEP 4: calcolo del centro di rigidezze e delle rigidezze globali

X_c = Σ_i k_vd_v / k_{v tot.}

Y_c =  Σ_i k_od_o / k_{o tot.}

Infine è possibile calcolare anche la rigidezza torsionale totale pari a:

k_Φ = Σ_ik_i dd_i²

 

 

STEP 5: analisi dei carichi sismici

Q = carico totale accidentale = q_a A_tot

 

STEP 6: ripartizione della forza sismica lungo l'asse x e lungo l'asse y

               F_y^O= K_y^O * dd_y^O * ϕ_y    per i controventi verticali

Ripartizione della forza sismica lungo l'asse X:

Ripartizione della forza sismica lungo l'asse Y:

Commerzbank Tower - Foster & Partners

In questo nuovo post continuiamo il discorso sulle travi Vierendeel, occupandoci in questo caso di un modello che preveda gli estremi incastrati ad ambo i lati. E' la scelta progettuale adottata tra gli altri da Foster & Partners per il progetto della Commerzbank Tower a Francoforte (1994-1997), la cui soluzione strutturale prevede una coppia di montanti verticali all’interno di ognuna delle strutture d’angolo, ai quali sono collegate travi Vierendeel da otto piani, che sorreggono i solai degli uffici da angolo ad angolo. Sicuramente una scelta audace ed onerosa, che permette però di avere diversi vantaggi, tra cui, ad esempio, la possibilità di fruire di un open space privo di pilastri all'interno degli uffici.

Vediamo quindi in sintesi come si comporta meccanicamente la trave doppiamente incastrata:

Si nota subito come nel nostro caso la trave sia perfettamente simmetrica attorno al montante verticale 1. Conosciamo inoltre, come segnalato nel precedente post, i valori del taglio e del momento e l'analisi della deformata di una trave doppiamente incastrata, che costituisce il singolo elemento della trave Vierendeel:

Dallo schema della deformata della singola trave possiamo facilmente ricavare la deformata di tutta la Vierendeel:

Per quanto riguarda il valore del taglio sui traversi, possiamo utilizzare il metodo empirico adottato anche con la precedente trave. Occorre però precisare come si ripartisce la forza F sul pilastro 1, che risulta essere il nostro asse di simmetria:

Una volta capito ciò, si può procedere con il calcolo dei valori del taglio agenti sui traversi, semplicente dividendo la forza agente su ogni tratto orizzontale per 2 e assegnandone una metà a ciascuno di essi:

Verifichiamo la correttezza del procedimento ancora una volta scrivendo l'equilibrio alla traslazione verticale, e sostituendo il valore nell'equazione del taglio derivante dallo schema notevole della trave doppiamente incastrata. Scriviamo solo i primi 3, perchè, essendo la struttura simmetrica, sarà sufficiente specchiarli per ottenere i rimanenti:

Passiamo ora ai momenti dei traversi. Come nel caso precedente, conoscendo i punti di nullo, sarà sufficiente moltiplicare il valore del taglio ottenuto per il braccio. Questo è il diagramma:

Per conoscere invece i valori dei momenti sui montanti, abbiamo bisogno di scrivere l'equilibrio ai nodi. Ancora una volta, data la simmetria della struttura, sarà sufficiente analizzare solo i primi 3:

Non ci rimane che trovare i valori delle forze taglianti dei montanti (sommando la coppia dei momenti agenti sul montante e dividendoli per la luce su cui lavorano) e diagrammarli:

 

Verifichiamo infine su SAP2000 di non aver commesso errori:

Taglio

Momento

Deformata

 

Villa Chardonne

Nel corso degli ultimi 30 anni diversi architetti, in linea con la loro più o meno velata adesione al movimento De Stijl e alle correnti da esso derivate, hanno costruito il loro successo e la loro affermazione in campo architettonico, grazie alla progettazione di architetture che ricorrono sistematicamente a sbalzi più o meno azzardati. Si è assistito quindi alla massiccia implementazione nelle nuove architetture di quei sistemi strutturali che, fino ad allora, erano una prerogativa esclusiva di ponti di notevole luce. In questa ottica, giocò un ruolo fondamentale la trave ideata dall'ingegnere belga Jules Arthur Vierendeel che la brevettò alla fine del 1800.

Essa consiste in un telaio a più campate costituito da travi continue alla testa ed ai piedi, e da una serie di montanti verticali che, dal punto di vista geometrico, la rendono assimiliabile ad una trave reticolare dalla quale vengono rimosse le aste diagonali; tale assenza comporterebbe la labilità del sistema ai carichi orizzontali nel caso di nodi che non impediscono le rotazioni (ad es. cerniere). Per rendere stabile questa trave, dunque, è necessario che i nodi siano rigidi, con conseguente trasmissione di momento flettente sulle aste; è proprio questa la differenza sostanziale tra travi reticolari e Vierendeel: le prime sono composte da elementi sottoposti a sollecitazioni di sola trazione o compressione, mentre nelle seconde le aste sono inflesse.

In questa esercitazione, quindi, vedremo qual è il comportamento di queste travi dal punto di vista meccanico. Nello specifico prendiamo in esame una trave Vierendeel con gli estremi di sinistra incastrati ad un supporto e quelli di destra liberi, come potrebbero essere ad esempio quelle adottate in Villa Chardonne di cui sopra:

Come detto in precedenza, questa trave, per l'enorme rigidezza dei montanti verticali, può essere assimilata ad un telaio SHEAR TYPE disposto orizzontalmente, e, come quest'ultimo, fa riferimento agli schemi notevoli della trave doppiamente incastrata, sia per quanto riguarda l'analisi della deformata sia per i valori del momento flettente e del taglio:

Dall'analisi della deformata della singola trave possiamo ricavare la deformata di tutta la trave Vierendeel:

Inoltre, in una Vierendeel costituita dallo stesso materiale e da traversi uguali (che hanno quindi la stessa rigidezza), possiamo rapidamente calcolare i valori del taglio di ogni traverso, semplicemente ripartendo in 2 la forza che agisce su ogni campata e assegnandola ai traversi in questione:

Verichiamo che il metodo utilizzato è corretto analizzando ogni singolo nodo e scrivendo l'equilibrio alla traslazione verticale, sostituendo poi ogni volta il valore del taglio trovato dentro l'equazione precedentemente ottenuta dallo schema notevole:

Lo schema della deformata ci da un'ulteriore informazione: nel punto di flesso sappiamo che la curvatura è 0. Quindi anche il momento, come riportato dallo schema notevole, è nullo nel punto medio del traverso. Per conoscere il valore massimo del momento, quindi, sarà sufficiente moltiplicare il valore del taglio di ogni campata per la metà del traverso (che nel nostro caso è L/2). Avremo quindi il seguente diagramma dei momenti:

Conoscendo i valori del momento sui traversi, possiamo trovare tramite l'equilibrio dei nodi i rispettivi valori dei momenti sui montanti verticali. Non sarebbe possibile ricavarli tramite l'equazione del momento del modello della trave di Bernoulli (M=EIX), in quanto, a causa dell'estrema rigidezza dei montanti (EI=infinito), avremmo un'equazione indeterminata. I momenti risultano essere quindi:

Una volta ottenuti i valori dei momenti sarà sufficiente bilanciare i montanti verticali con una coppia di forze taglianti, il cui valore è sempre ricavabile tramite questo semplice metodo:

Analizzando quindi ogni singolo nodo, avremo i seguenti valori per il taglio:

Grazie ai valori del taglio appena trovati, sappiamo anche quanto vale lo sforzo normale sui traversi, in quanto secondo il principio dell'equilibrio dei nodi ciò che è taglio diventa sforzo normale e viceversa. Il diagramma sarà perciò questo:

Come si nota dal diagramma, i traversi orizzontali sono tesi, mentre quelli inferiori sono compressi.

Ora non ci rimane che verificare la bontà del metodo utilizzato, disegnando su SAP2000 la nostra trave Vierendeel e ricordandoci di modificare il modulo elastico (E) del materiale che utilizzeremo per i pilastri verticali, assegnandogli un valore molto alto. Di seguito riporto i diagrammi di sforzo normale, taglio e momento e l'analisi della deformata:

SFORZO NORMALE

TAGLIO

MOMENTO FLETTENTE

DEFORMATA

 

In questa nuova esercitazione siamo chiamati a risolvere una struttura 3 volte iperstatica, tramite il metodo delle forze. La struttura in questione è una trave su più appoggi, molto comune nella progettazione strutturale ordinaria:

 

Per trovare le reazioni vincolari di questa struttura (che nel caso in cui fosse risolta col metodo della linea elastica comporterebbe un'innumerevole quantità di calcoli) adottiamo quindi il METODO DELLE FORZE. Per prima cosa trasformiamo l'attuale sistema iperstatico in un equivalente isostatico, a cui aggiungiamo, sottoforma di forze esterne, le reazioni vincolari in eccesso:

Nel nostro caso è più opportuno trasformare l'unica trave di luce 4 L in quattro travi di luce L, collegate tra loro da carrelli, e aggiungere, sempre come forze esterne, le reazioni vincolari rimosse. Il sistema sarà così assimilabile ad una serie di travi doppiamente appoggiate, con l'aggiunta di coppie di momenti di forze in corrispondenza dei punti B, C,  D. Avremo quindi 2 schemi, che andremo poi a sommare tramite il metodo della sovrapposizione degli effetti:

Inoltre, se analizziamo la struttura dal punto di vista qualitativo, si nota subito che essa è caratterizzata da una marcata simmetria, la quale ci consente di affermare che le reazioni vincolari sono rispettivamente uguali in B e D,  ed in A ed E. Sempre grazie alla simmetria, possiamo anche affermare che la coppia di momenti X₁ è uguale alla coppia X₂, e che quindi:

Dall'equazione cinematica del vincolo rimosso sappiamo invece che:

Prima di determinare quanto valgono le rotazioni complessive nei vari tratti, prendiamo dalle tavole sinottiche i valori delle rotazioni per la trave doppiamente appoggiata:

Una volta stabiliti, nel caso della trave doppiamente appoggiata, i valori delle rotazioni dovuti al carico q e alle coppie di momenti X, possiamo ricavarci i valori delle incognite iperstatiche X nei punti B e C:

 

 

Dopo aver trovato i valori delle incognite iperstatiche, abbiamo tutti gli strumenti necessari a determinare i valori delle reazioni vincolari:

Per il metodo della sovrapposizione degli effetti su enunciato, sommiamo quindi le reazioni vincolari dei 2 schemi:

Non rimane altro che disegnare i diagrammi di taglio e momento flettente:

House in Akiya - Architect Cafe/Mikio Tai

Il legno, unitamente alla pietra, è stato uno dei primi materiali a cui l'architettura si è rivolta ed era anche l'unico che poteva indifferentemente essere impiegato a compressione, a trazione e, soprattutto, a flessione. Quando nell'Ottocento, grazie anche al contributo della teoria delle strutture, si raggiungono elevate luci con le strutture in legno (capriate, reticolari rettilinee, cupole reticolari e strutture lamellari), l'introduzione della ghisa e dell'acciaio ne decretano il declino, situazione che è rimasta tale fino alla seconda metà del Novecento con la diffusione del legno lamellare. Nonostante le ampie possibilità di grande luci con il legno lamellare (sono stati superati i 70 metri di luce con cupole in lamellare) anche il legno naturale ha ritrovato nuove applicazioni soprattutto nelle regioni in cui è rimasto vivo l'insegnamento della tradizione come in Finlandia e in centro Europa (Baviera, Austria, Svizzera). Analogamente in Giappone, luogo di antichissima tradizione costruttiva con il legno, diversi architetti sono attualmente impegnati nella rielaborazione delle soluzioni costruttive con questo materiale.

In questa esercitazione proveremo a predimensionare una trave in legno di un'abitazione con struttura a telaio. Ci verrà in soccorso un foglio di calcolo excel, molto utile nella prima fase della progettazione di un edificio, per farsi un'idea riguardo le probabili dimensioni da adottare. La pianta strutturale dell'abitazione in questione è così progetatta:

 

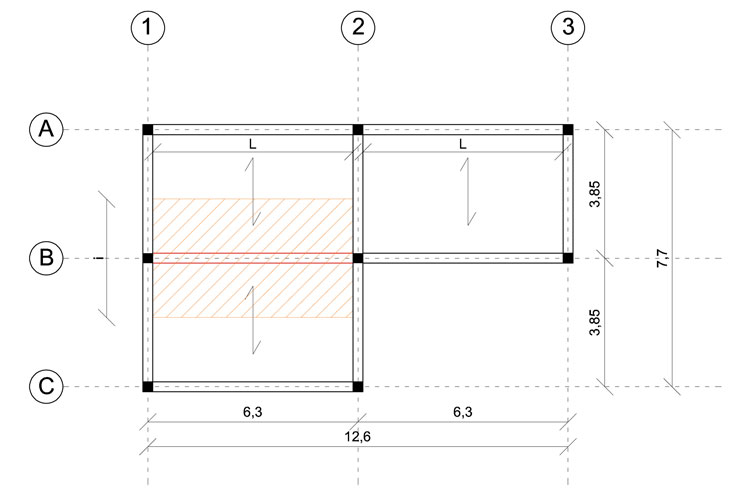
La trave in questione è la 1-2 sull'allineamento B. Prima di poter inserire qualsivoglia dato sul foglio excel, dobbiamo analizzare i carichi che gravano sulla trave:

Carico strutturale (Q_s), che indica l'entità del carico intrinseco di tutti gli elementi componenti la struttura che gravano sulla trave;

Carico permanente (Q_p), che indica l'entità del carico di tutti gli elementi che compongono il solaio, ma che non hanno funzione strutturale, con l'aggiunta eventuale del sovraccarico di tutte le partizioni interne al di sopra del solaio;

Carico accidentale (Q_a), che indica l'entità del carico di tutti gli elementi variabili al di sopra della trave, quali, ad esempio, arredi, persone, agenti atmosferici.

A parte il carico accidentale (il cui valore è prestabilito dalla normativa, in base alla destinazione d'uso del manufatto architettonico), dobbiamo ricavarci gli altri due tramite dei semplici calcoli, che variano a seconda della stratigrafia del solaio. Ipotizziamo che il nostro solaio sia strutturato in questo modo:

 

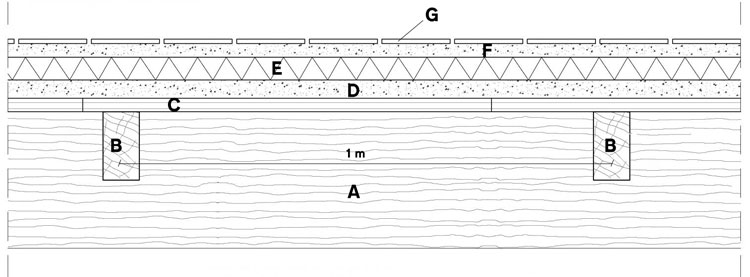
A = Trave in legno lamellare;

B= Travetti in legno lamellare;

C= Assito in legno di castagno;

D= Caldana in calcestruzzo;

E= Isolante termo acustico;

F= Massetto di allettamento in calcestruzzo;

G= Pavimento in legno di rovere.

 

Nel caso specifico di un solaio in legno a doppia orditura, per il corretto calcolo del carico strutturale gravante sulla trave, abbiamo bisogno di definire prima, sempre con lo stesso foglio di calcolo, le dimensioni dei travetti.

 

PREDIMENSIONAMENTO DEI TRAVETTI

Carico strutturale Q_s

Assito in legno di castagno (s = 0.035 m)      P = V x g = (1m x 1m x 0,035m) x 6 kN/mc        Q_s = 0,21 kN/mq

Carico permanente Q_p

Pavimento in parquet di rovere (s = 0,02 m)            8 KN/mc x 0,02 m = 0,16 kN/mq

Massetto (s =0,03 m)                                             20 KN/mc x 0,03 m = 0,6 kN/mq

Isolante termo-acustico (s= 0,05 m)                      0,6 KN/mc x 0,05 m = 0,03 kN/mq

Caldana (s= 0,04 m)                                              10 KN/mc x 0,04 m = 0,4 kN/mq

Impianti                                                                    (da normativa)        0,5 kN/mq 

Tramezzi                                                                  (da normativa)           1 kN/mq 

Q_p = 2,69 kN/mq

Carico accidentale Q_a = per civile abitazione la normativa stabilisce Q_a = 2 kN/mq

Sommando i carichi avremo quindi:

Q_tot = 0,21 + 2 + 2,69 = 4,90 kN/mq

Una volta trovato il carico distribuito incidente su 1 mq di superficie, moltiplico il valore per l'area di influenza i, al fine di trovare il valore del carico lineare che grava sul singolo travetto:

Q = 3,90 kN/mq x 1 m = 4,90 kN/m

A questo punto scegliamo la classe di resistenza del legno lamellare per i travetti, una GL240 con resistenza caratteristica a flessione di 24 N/mmq. Inseriamo nel foglio excel anche il valore del K_mod (una variabile che tiene conto del fatto che il legno è un materiale organico, e quindi soggetto a deterioramento) ed esso, tramite la formula:

f_d = K_mod x fk / γ_m = 0,6 x 24 N/mmq / 1,45 = 9,93 N/mmq

calcola la tensione di progetto massima. Ipotizziamo, inoltre, che il sistema di fissaggio del travetto alla trave sia assimilabile a quello di una trave doppiamente appoggiata; ne ricaviamo che il momento flettente è pari QL^2/8. Non rimane altro che inserire la luce del nostro travetto (3,85 m) e ipotizzare una base per il predimensionamento (0,12 m):

Approssimiamo h e avremo un travetto predimensionato di 12 x 25 cm. Verifichiamo ora che la sezione del travetto sia corretta, sommando al Q_s iniziale il carico del travetto al metro quadro:

Travetto in legno lamellare di conifere      Q_travetto = [(0,12 m x 0,25 m x 1 m) x 3,73 kN/mc] / 1 mq = 0,11 kN/mq

Q_s' = Q_s + Q_travetto = 0,32 kN/mq

Il travetto risulta quindi verificato: GL24h 12x25 cm. Passiamo ora al predimensionamento della trave.

PREDIMENSIONAMENTO DELLA TRAVE

Una volta dimensionati i travetti, non rimane che trovare la sezione della trave, ripetendo lo stesso procedimento:

Carico strutturale Q_s

Assito in legno di castagno (s = 0.035 m)      (1m x 1m x 0,035m) x 6 kN/mc = 0,21 kN/mq   

Travetto in legno lamellare di conifere            (0,12 m x 0,25 m x 1 m) x 3,73 kN/mc = 0,11 kN/mq

Q_s = 0,32 kN/mq

Carico permanente Q_p

Pavimento in parquet di rovere (s = 0,02 m)            8 KN/mc x 0,02 m = 0,16 kN/mq

Massetto (s =0,03 m)                                             20 KN/mc x 0,03 m = 0,6 kN/mq

Isolante termo-acustico (s= 0,05 m)                      0,6 KN/mc x 0,05 m = 0,03 kN/mq

Caldana (s= 0,04 m)                                              10 KN/mc x 0,04 m = 0,4 kN/mq

Impianti                                                                    (da normativa)        0,5 kN/mq 

Tramezzi                                                                  (da normativa)           1 kN/mq 

Q_p = 2,69 kN/mq

Carico accidentale Q_a = 2 kN/mq

Sommando i carichi avremo quindi:

Q_tot = 0,32 + 2 + 2,69 = 5,01 kN/mq

Anche in questo caso, per trovare il carico che grava su 1 metro lineare di trave, moltiplico il carico distribuito per l'area di influenza della trave (i):

Q = 5,01 kN/mq x 3,55 m = 17,78 kN/m

Scegliamo anche per la trave un legno lamellare con classe di resistenza GL240 e calcoliamo, come in precedenza, il momento per una trave doppiamente appoggiata. Inseriamo la luce della trave (6 m) e ipotizziamo una base di partenza di 30 cm:

Approssimiamo h anche per la trave e ipotizziamo una trave di legno lamellare di 30 x 45 cm. Procediamo alla verifica allo stesso modo, aggiungendo il peso proprio della trave al Q_s precedente:

Trave in legno lamellare di conifere      Q_trave = [(0,30 m x 0,45 m x 1 m) x 3,73 kN/mc] / 1 mq = 0,50 kN/mq

Q_s' = Q_s + Q_trave = 0,82 kN/mq

La trave risulta quindi verificata: GL24h 30x45 cm.

 La Cacciata di Adamo ed Eva dal Giardino del Paradiso - Alexandre Cabanel

Chissà a che livelli arrivò la frustrazione di Adamo ed Eva nell'ascoltare la sentenza di Dio, riguardante il loro definitivo allontanamento dal Paradiso Terrestre. Allora erano forse inconsapevoli del fatto che, a causa di quel gesto di superbia, avevano perduto per sempre i doni preternaturali, i quali, tra le altre cose, li mettevano al riparo da ignoranza e inettitudine. Sicuramente non immaginavano di aver abbandonato, col loro atto, una parte del genere umano alle frustrazioni causate dal burrascoso rapporto con la meccanica e la statica. Diverse generazioni di studenti di architettura hanno convissuto con lo spauracchio degli esami di queste due discipline. Spauracchio che puntualmente si acuiva nel momento in cui venivano pronunciate due parole: LINEA ELASTICA.

Nonostante il senso di inquietudine che ancora mi pervade, proverò in questo post a spiegare come affrontare un sistema iperstatico, tramite l'utilizzo, appunto, dell'equazione della linea elastica. Iniziamo.

Questo era il sistema iperstatico assegnato, in cui dovevamo trovare il valore dello spostamento verticale v e ricavare un disegno della deformata, da verificare poi in SAP2000.

Scriviamo innanzitutto le equazioni relative al modello della trave di Bernoulli.

Equazioni differenziali di bilancio:

Equazioni del legame costitutivo:

Equazioni di congruenza:

Eliminiamo dal sistema le equazioni relative allo sforzo normale, dato che non prendiamo in considerazione l'analisi della deformata assiale, e mettiamo a sistema le rimanenti:

Partiamo dalla 2° equazione:

Sostituendo nella precedente:

Imponiamo che q2 sia costante, e,integrando 4 volte l'equazione differenziale ottenuta qui sopra, possiamo ricavare l'equazione esplicitata in v(s), che ci permetterà poi di ricavare tutte le altre incognite:

Scriviamo quindi le condizioni al bordo nei punti s=0 e s=L, per trovare i valori delle varie costanti c.

Per s=0:

Per la condizione s=L, mettiamo a sistema le 2 equazioni:

Sapendo che lo spostamento v ha un massimo o un minimo dove la pendenza della tangente alla deformata è nulla, poniamo l'equazione della rotazione pari a 0, per trovare un valore accettabile di s:

Supponiamo inoltre che la sezione della trave sia costante e dello stesso materiale, cosicchè possiamo sostituire ad I la formula del momento di inerzia di una sezione generica:

Consideriamo solo s=0,57, in quanto s<1, e lo andiamo a sostituire nell'equazione differenziale precedente per trovare v(s):

Disegniamo i diagrammi del taglio e del momento, da confrontare poi con quelli di SAP2000, impostando q₂=-q e calcolando i relativi valori:

Per le condizioni al bordo, M è nullo in:

Troviamo anche i valori del taglio, sapendo che esso è la derivata del momento, consapevoli del fatto che nel punto in cui il taglio è nullo, il momento è invece massimo:

Dopo la parte dei calcoli manuali (poco piacevole, a dir la verità), portiamo il tutto su SAP2000, verificando di non aver sbagliato nulla.

Apriamo innanzitutto un nuovo file basato su griglia e andiamo nella vista 2D xz. Tramite lo strumento POINT inseriamo un punto in corrispondenza del vmax che usciva fuori dai precedenti calcoli (0,57L), e, grazie allo snap dei 3 punti, disegniamo la nostra trave (DRAW-FRAME):

Ora assegniamo una sezione generica IPE alla trave in acciaio (DEFINE-SECTION PROPERTIES-FRAME SECTIONS):

Dopo  aver assegnato i vincoli e rimosso l'analisi del carico proprio della struttura, come al solito, impostiamo la densità di carico q₂ per la trave:

Ora non ci resta che avviare l'analisi della deformata, ricordandoci prima di rimuovere dall'analisi il MODAL:

In ultimo, lasciamo che SAP2000 ci calcoli i diagrammi del momento flettente e del taglio, per verificare di averli disegnati correttamente in precedenza: