GRATICCIO DI TRAVI. Esercitazione manuale + SAP2000

Padiglione della Fiera di Rimini - GMP Architekten

Dopo aver iniziato a trattare la torsione nel precedente post, vediamo in questo caso quali sono le implicazioni di tale tensione su un sistema più complesso, quale il graticcio. Gli impalcati a graticcio sono costituiti da un numero variabile di travi longitudinali, fra loro affiancate e collegate puntualmente da elementi irrigidenti trasversali, detti traversi. Le travi principali, poste ad interasse i, ed i traversi, posti ad interasse j, formano una maglia generalmente rettangolare pari a ixj. Dal punto di vista del comportamento strutturale, gli impalcati a graticcio hanno una minore rigidezza torsionale rispetto a quelli a cassone e rispetto le travi reticolari spaziali, ma sono sicuramente un giusto compromesso tra i sistemi a telaio ordinari e strutture più ardite, senza trascurare l'oggettiva e significativa istanza estetica di tali sistemi: è esemplificativa in merito la copertura dei padiglioni della Fiera di Rimini (vd. foto).

In questa esercitazione proveremo a risolvere manualmente uno stralcio dell'impalcato, verificando in seguito la bontà del procedimento eseguito tramite SAP2000. Lo schema in questione è il seguente:

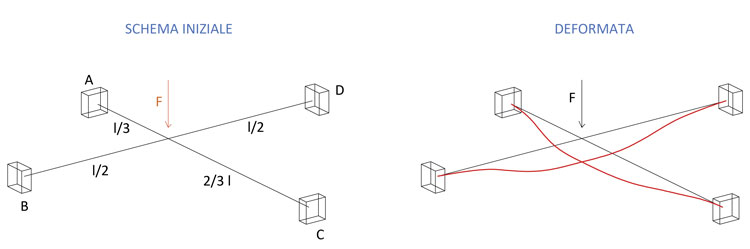
Per la deformata e i valori di taglio e momento, ci riferiamo agli ormai celebri schemi notevoli della trave doppiamente incastrata:

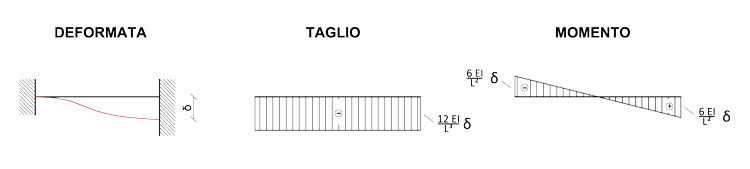
In questo caso abbiamo però una complicazione. Le due travi del graticcio si intersecano ad 1/3 della trave AC, permettendo così alla forza applicata nel nodo di generare una rotazione ϕy. Il risultato della deformata nella trave AC sarà quindi uguale alla somma dell'abbassamento δ e della rotazione ϕy, mentre sulla trave BD agirà esclusivamente l'abbassamento, in virtù della curvatura χ=0 in corrispondenza del punto di applicazione della forza:
 

 
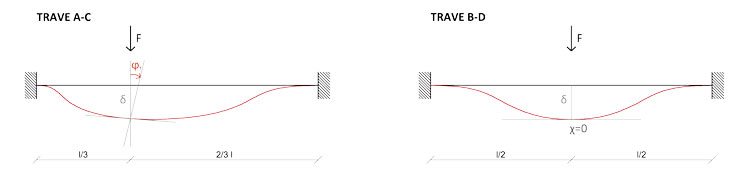
Ai fini dello svolgimento dell'esercizio sarà quindi opportuno separare l'azione dei due diversi effetti, per poi sovrapporli alla fine. Iniziamo dall'abbassamento δ sulla trave AC:

Passiamo ora all'abbassamento δ sulla trave BD:

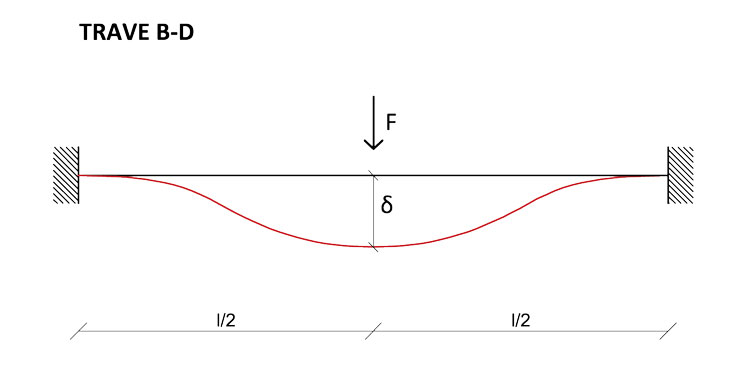
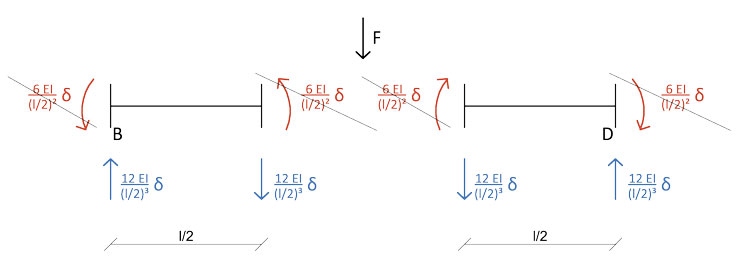
Nel caso della trave BD, i momenti flettenti si annullano l'uno con l'altro e verranno quindi ignorati nella successiva equazione di equilibrio alla rotazione. Lasciamo agire ora solo la rotazione ϕy sulla trave AC, riferendoci agli schemi notevoli della rotazione su una trave doppiamente incastrata:

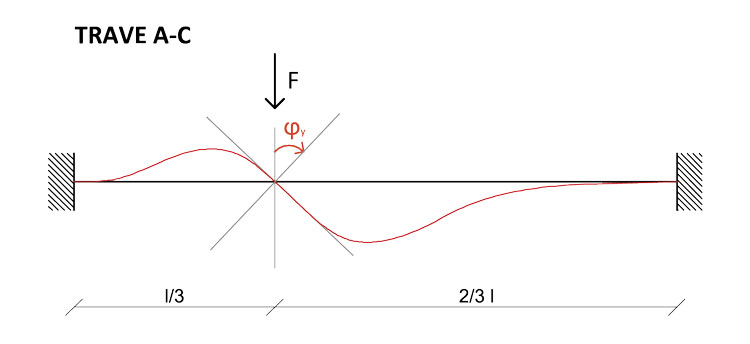
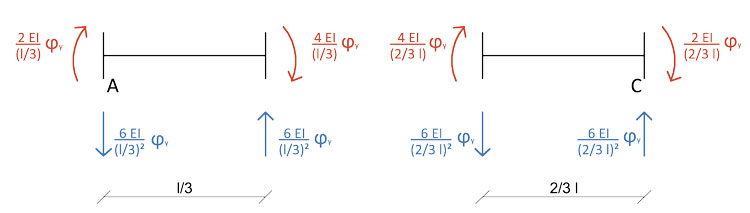
Come già spiegato in precedenza, la trave BD è esente da sollecitazioni rotazionali, ma sappiamo anche che la flessione sull'asse x provoca inevitabilmente la torsione sull'asse perpendicolare, su cui giace la trave in questione:

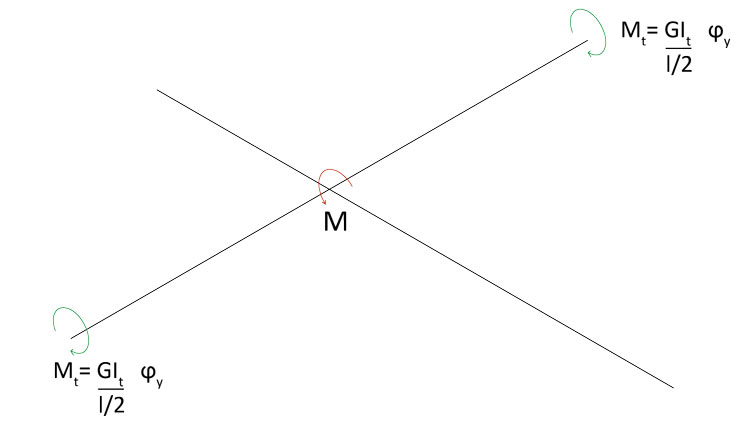
La trave reagirà quindi alla sollecitazione con un momento torcente di verso opposto alla rotazione ϕy.

Dopo aver esaminato tutti gli effetti separatamente, possiamo ora sovrapporli tra di loro, scrivendo prima l'equazione di equilibrio alla traslazione verticale e poi quella di equilibrio alla rotazione:

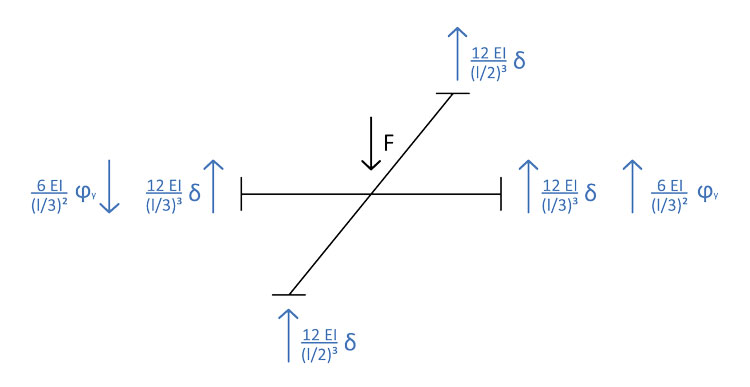
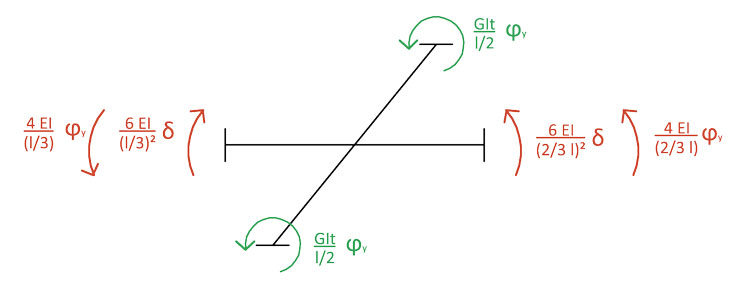
Abbiamo quindi un sistema di 2 equazioni in 2 incognite. Per non affrontare tutto il calcolo a mano si è scelto di adottare il software Mathematica 8, tramite il quale ricavare i valori delle incognite ϕy e δ:

Quindi:

                                          δ = 2Fl³/1113EI                                       ϕy = 9Fl²/742 (3EI+4I_t )

Non ci rimane che portare il nostro semplice graticcio su SAP2000, per vedere come varia l'abbassamento e la rotazione del nodo a cui è applicata la forza, in funzione della rigidezza del sistema intero, che ricordiamo essere la somma della rigidezza flessionale e della rigidezza torsionale. Iniziamo disegnando l'impalcato con delle sezioni generiche, e verificando la congruenza della deformata e dei diagrammi delle sollecitazioni:

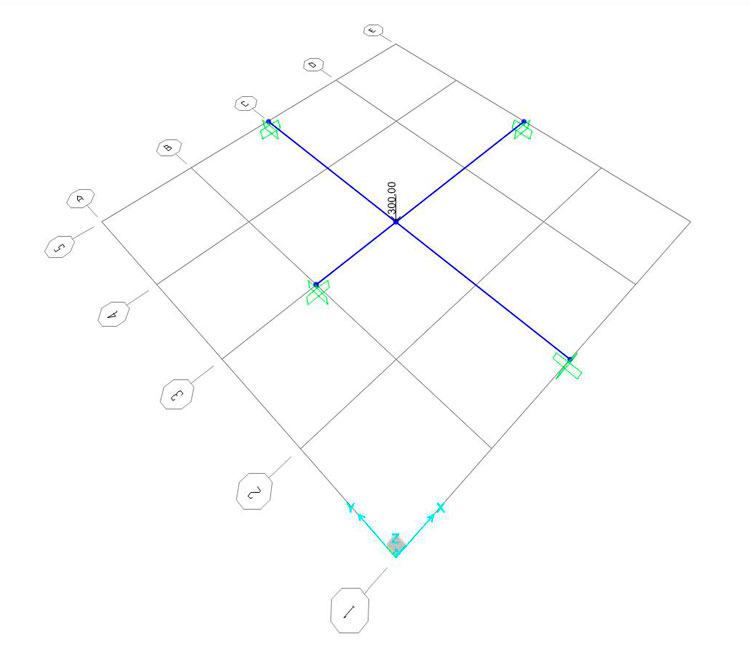
Deformata:

Taglio:

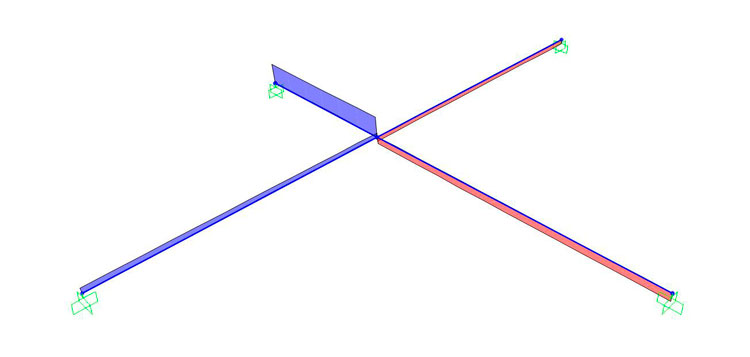
Momento:

Lasciando sempre fissa la sezione della trave AC (IPE500), variamo la sezione della BD e riportiamo i valori dell'abbassamento e della rotazione del nodo d'intersezione su un'apposita tabella. Come sezioni di prova adotteremo una IPE500, una scatolare e una tubolare:

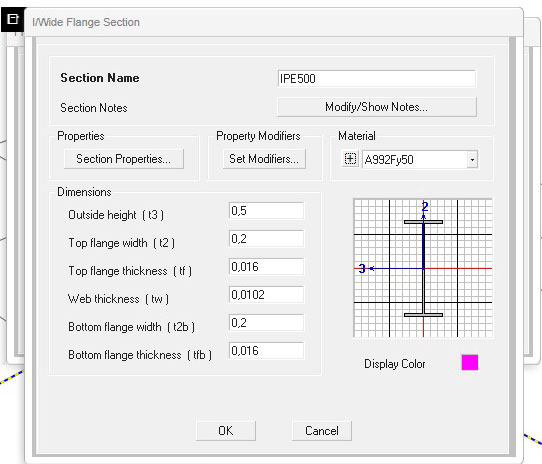
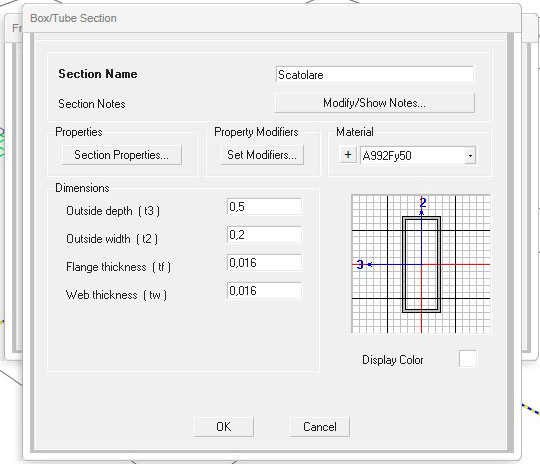
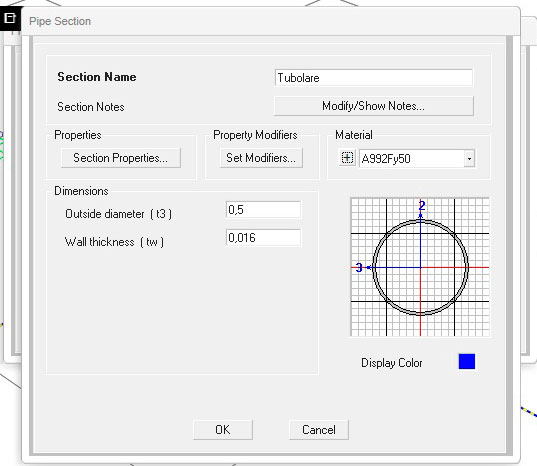
Come già dimostrato nella precedente esercitazione, i profili chiusi (ed in particolare i profili tubolari) offrono una maggiore rigidezza torsionale, che, inevitabilmente, comporta anche un minore abbassamento del nodo d'intersezione delle travi.