TRAVE VIERENDEEL DOPPIAMENTE INCASTRATA. Esercitazione manuale + Sap2000

Commerzbank Tower - Foster & Partners

In questo nuovo post continuiamo il discorso sulle travi Vierendeel, occupandoci in questo caso di un modello che preveda gli estremi incastrati ad ambo i lati. E' la scelta progettuale adottata tra gli altri da Foster & Partners per il progetto della Commerzbank Tower a Francoforte (1994-1997), la cui soluzione strutturale prevede una coppia di montanti verticali all’interno di ognuna delle strutture d’angolo, ai quali sono collegate travi Vierendeel da otto piani, che sorreggono i solai degli uffici da angolo ad angolo. Sicuramente una scelta audace ed onerosa, che permette però di avere diversi vantaggi, tra cui, ad esempio, la possibilità di fruire di un open space privo di pilastri all'interno degli uffici.

Vediamo quindi in sintesi come si comporta meccanicamente la trave doppiamente incastrata:

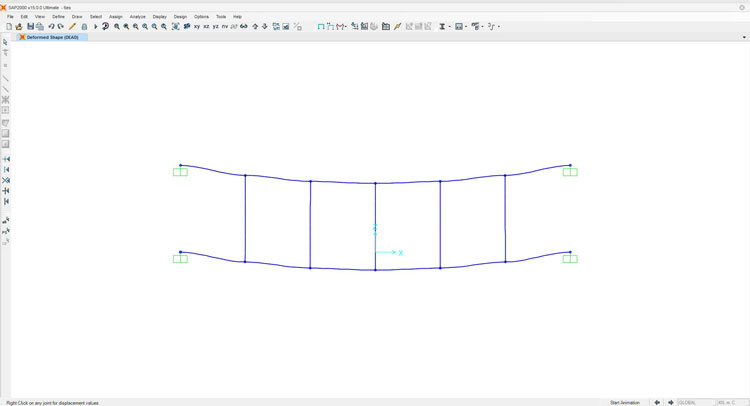
Si nota subito come nel nostro caso la trave sia perfettamente simmetrica attorno al montante verticale 1. Conosciamo inoltre, come segnalato nel precedente post, i valori del taglio e del momento e l'analisi della deformata di una trave doppiamente incastrata, che costituisce il singolo elemento della trave Vierendeel:

Dallo schema della deformata della singola trave possiamo facilmente ricavare la deformata di tutta la Vierendeel:

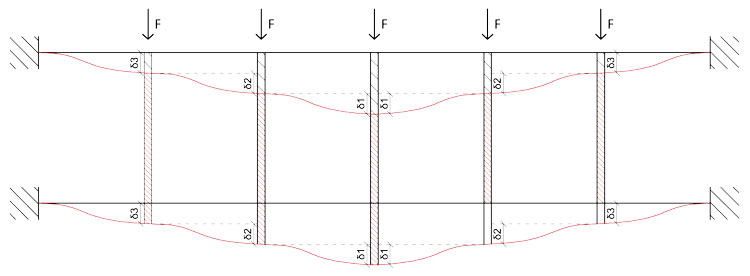
Per quanto riguarda il valore del taglio sui traversi, possiamo utilizzare il metodo empirico adottato anche con la precedente trave. Occorre però precisare come si ripartisce la forza F sul pilastro 1, che risulta essere il nostro asse di simmetria:

Una volta capito ciò, si può procedere con il calcolo dei valori del taglio agenti sui traversi, semplicente dividendo la forza agente su ogni tratto orizzontale per 2 e assegnandone una metà a ciascuno di essi:

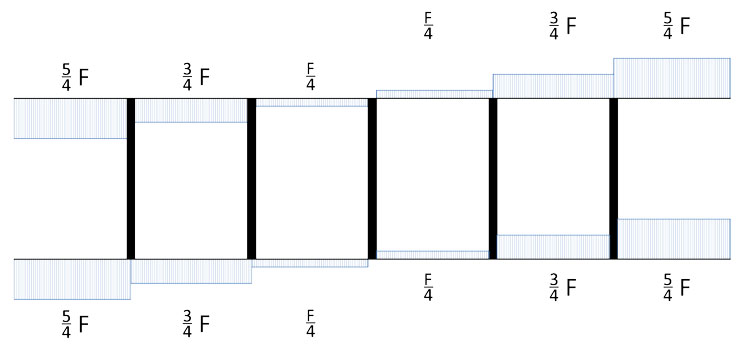
Verifichiamo la correttezza del procedimento ancora una volta scrivendo l'equilibrio alla traslazione verticale, e sostituendo il valore nell'equazione del taglio derivante dallo schema notevole della trave doppiamente incastrata. Scriviamo solo i primi 3, perchè, essendo la struttura simmetrica, sarà sufficiente specchiarli per ottenere i rimanenti:

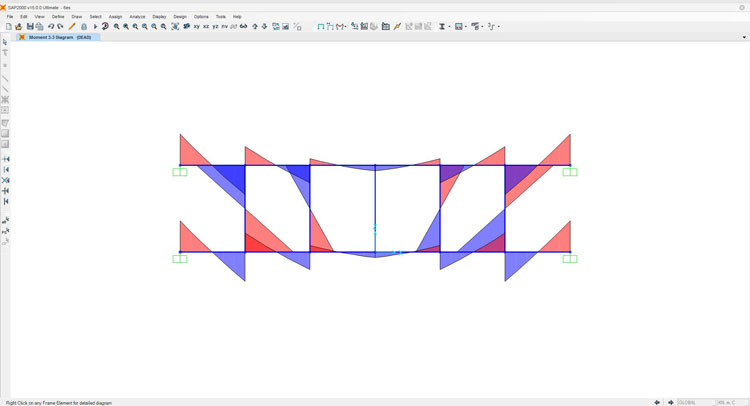
Passiamo ora ai momenti dei traversi. Come nel caso precedente, conoscendo i punti di nullo, sarà sufficiente moltiplicare il valore del taglio ottenuto per il braccio. Questo è il diagramma:

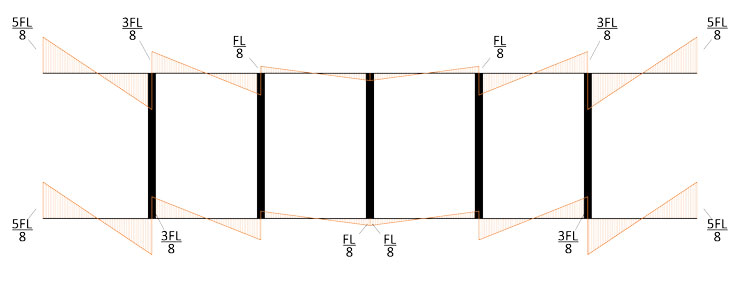
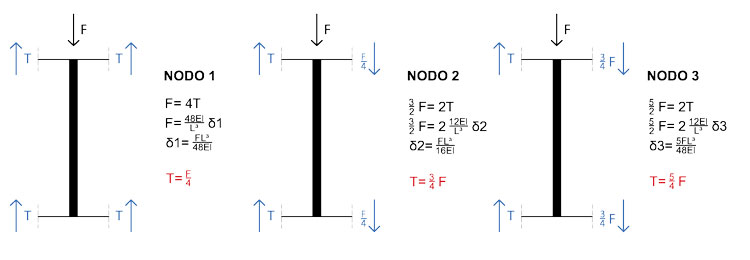
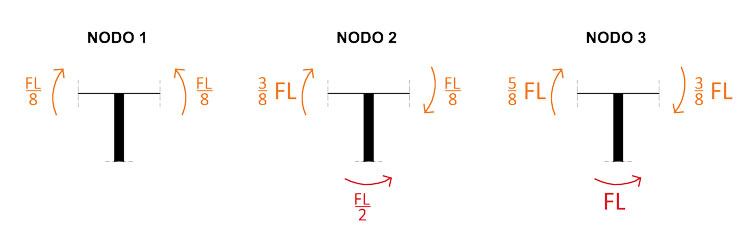
Per conoscere invece i valori dei momenti sui montanti, abbiamo bisogno di scrivere l'equilibrio ai nodi. Ancora una volta, data la simmetria della struttura, sarà sufficiente analizzare solo i primi 3:

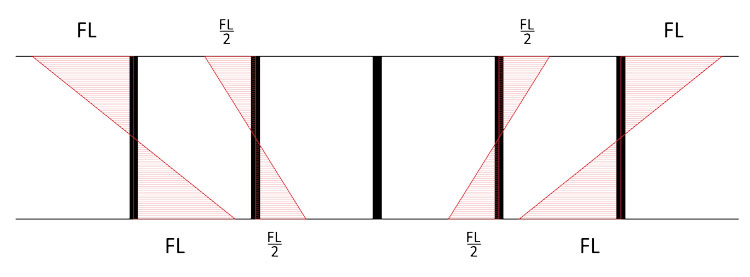
Non ci rimane che trovare i valori delle forze taglianti dei montanti (sommando la coppia dei momenti agenti sul montante e dividendoli per la luce su cui lavorano) e diagrammarli:

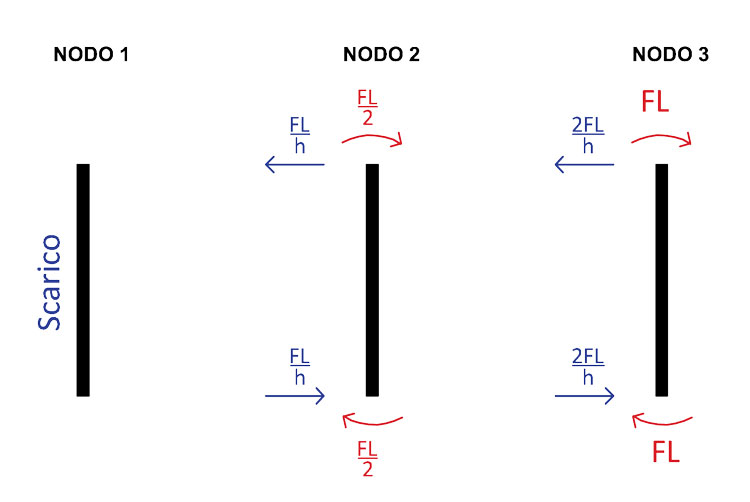
Verifichiamo infine su SAP2000 di non aver commesso errori:

Taglio

Momento

Deformata