TRAVE VIERENDEEL A SBALZO. Esercitazione manuale + Sap2000

Villa Chardonne

Nel corso degli ultimi 30 anni diversi architetti, in linea con la loro più o meno velata adesione al movimento De Stijl e alle correnti da esso derivate, hanno costruito il loro successo e la loro affermazione in campo architettonico, grazie alla progettazione di architetture che ricorrono sistematicamente a sbalzi più o meno azzardati. Si è assistito quindi alla massiccia implementazione nelle nuove architetture di quei sistemi strutturali che, fino ad allora, erano una prerogativa esclusiva di ponti di notevole luce. In questa ottica, giocò un ruolo fondamentale la trave ideata dall'ingegnere belga Jules Arthur Vierendeel che la brevettò alla fine del 1800.

Essa consiste in un telaio a più campate costituito da travi continue alla testa ed ai piedi, e da una serie di montanti verticali che, dal punto di vista geometrico, la rendono assimiliabile ad una trave reticolare dalla quale vengono rimosse le aste diagonali; tale assenza comporterebbe la labilità del sistema ai carichi orizzontali nel caso di nodi che non impediscono le rotazioni (ad es. cerniere). Per rendere stabile questa trave, dunque, è necessario che i nodi siano rigidi, con conseguente trasmissione di momento flettente sulle aste; è proprio questa la differenza sostanziale tra travi reticolari e Vierendeel: le prime sono composte da elementi sottoposti a sollecitazioni di sola trazione o compressione, mentre nelle seconde le aste sono inflesse.

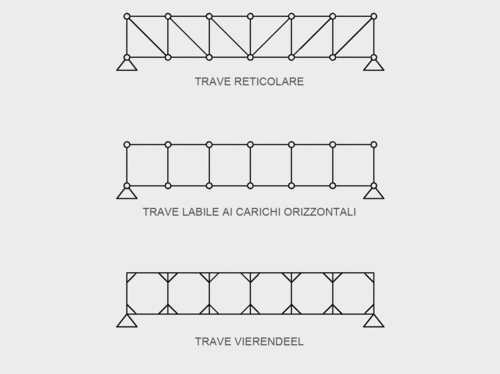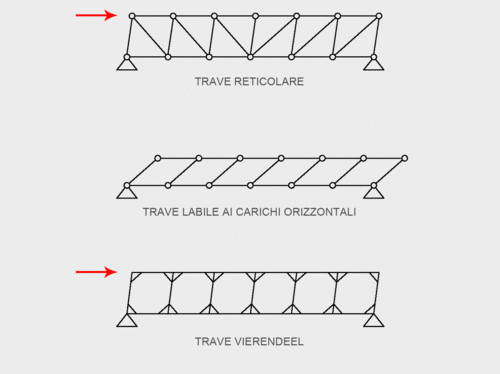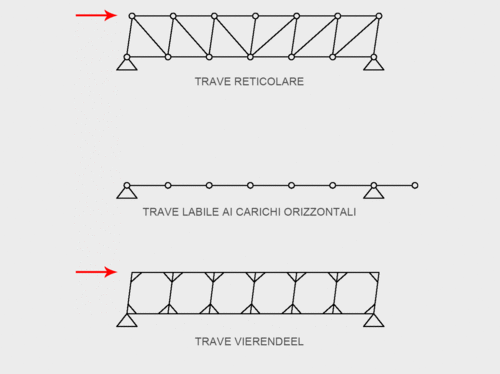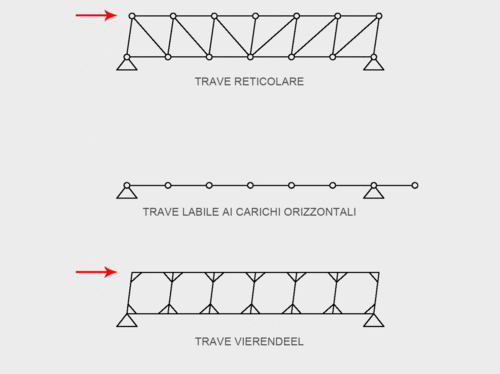
In questa esercitazione, quindi, vedremo qual è il comportamento di queste travi dal punto di vista meccanico. Nello specifico prendiamo in esame una trave Vierendeel con gli estremi di sinistra incastrati ad un supporto e quelli di destra liberi, come potrebbero essere ad esempio quelle adottate in Villa Chardonne di cui sopra:

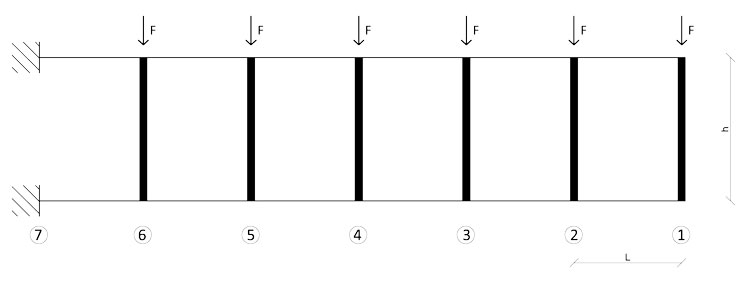Come detto in precedenza, questa trave, per l'enorme rigidezza dei montanti verticali, può essere assimilata ad un telaio SHEAR TYPE disposto orizzontalmente, e, come quest'ultimo, fa riferimento agli schemi notevoli della trave doppiamente incastrata, sia per quanto riguarda l'analisi della deformata sia per i valori del momento flettente e del taglio:

Dall'analisi della deformata della singola trave possiamo ricavare la deformata di tutta la trave Vierendeel:

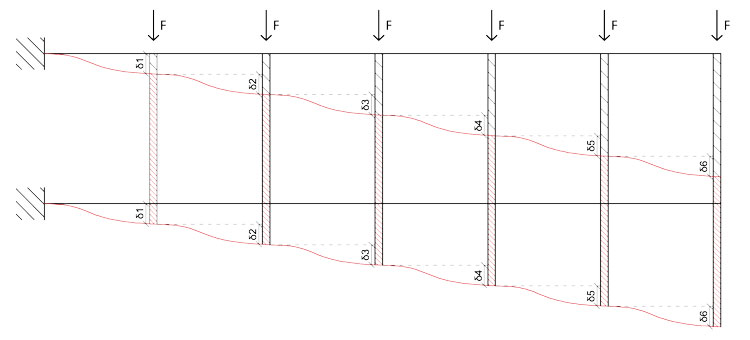
Inoltre, in una Vierendeel costituita dallo stesso materiale e da traversi uguali (che hanno quindi la stessa rigidezza), possiamo rapidamente calcolare i valori del taglio di ogni traverso, semplicemente ripartendo in 2 la forza che agisce su ogni campata e assegnandola ai traversi in questione:

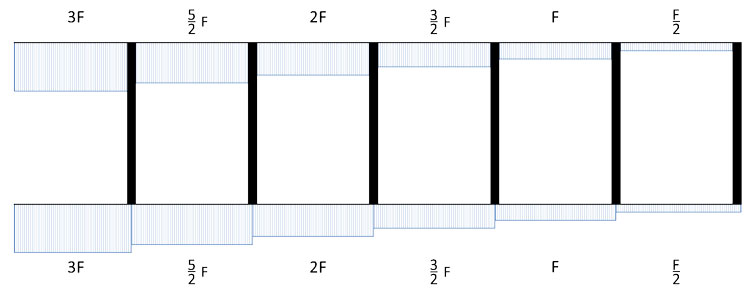
Verichiamo che il metodo utilizzato è corretto analizzando ogni singolo nodo e scrivendo l'equilibrio alla traslazione verticale, sostituendo poi ogni volta il valore del taglio trovato dentro l'equazione precedentemente ottenuta dallo schema notevole:

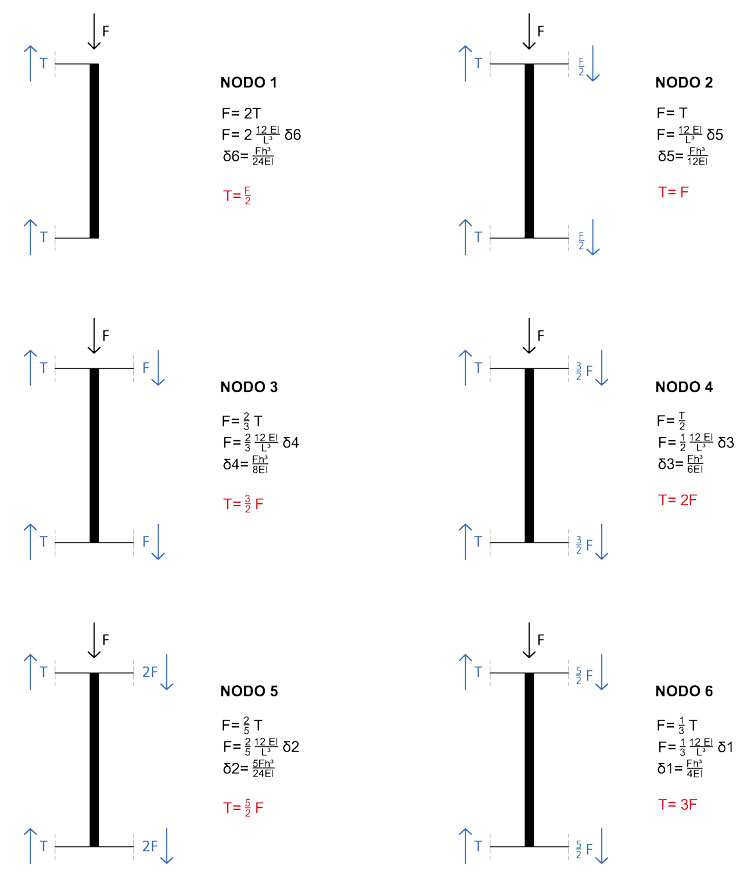
Lo schema della deformata ci da un'ulteriore informazione: nel punto di flesso sappiamo che la curvatura è 0. Quindi anche il momento, come riportato dallo schema notevole, è nullo nel punto medio del traverso. Per conoscere il valore massimo del momento, quindi, sarà sufficiente moltiplicare il valore del taglio di ogni campata per la metà del traverso (che nel nostro caso è L/2). Avremo quindi il seguente diagramma dei momenti:

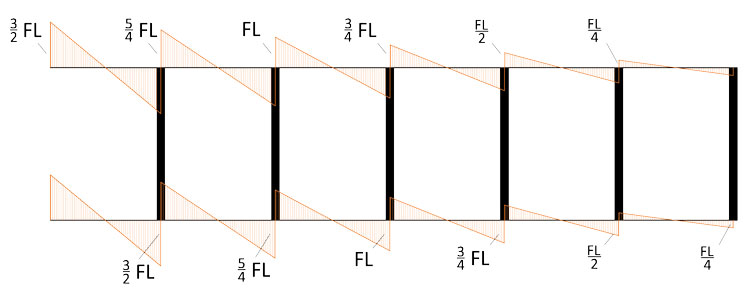
Conoscendo i valori del momento sui traversi, possiamo trovare tramite l'equilibrio dei nodi i rispettivi valori dei momenti sui montanti verticali. Non sarebbe possibile ricavarli tramite l'equazione del momento del modello della trave di Bernoulli (M=EIX), in quanto, a causa dell'estrema rigidezza dei montanti (EI=infinito), avremmo un'equazione indeterminata. I momenti risultano essere quindi:

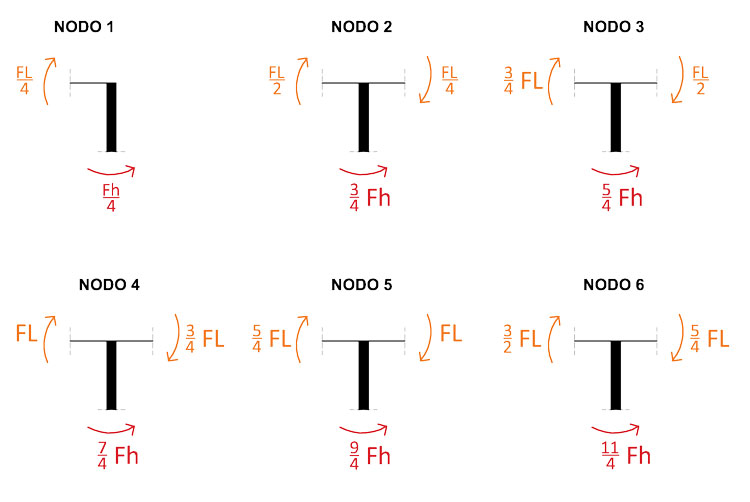
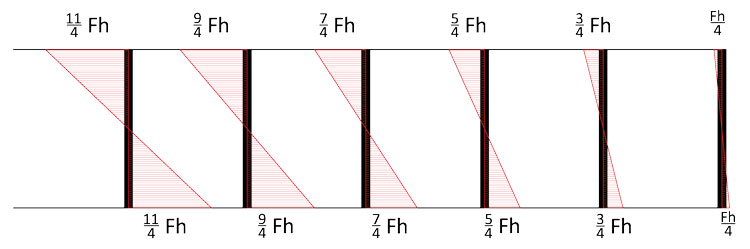
Una volta ottenuti i valori dei momenti sarà sufficiente bilanciare i montanti verticali con una coppia di forze taglianti, il cui valore è sempre ricavabile tramite questo semplice metodo:

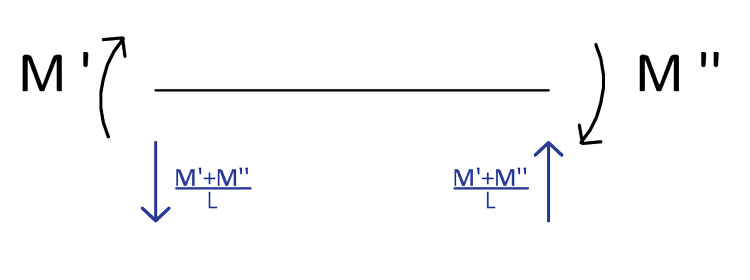
Analizzando quindi ogni singolo nodo, avremo i seguenti valori per il taglio:

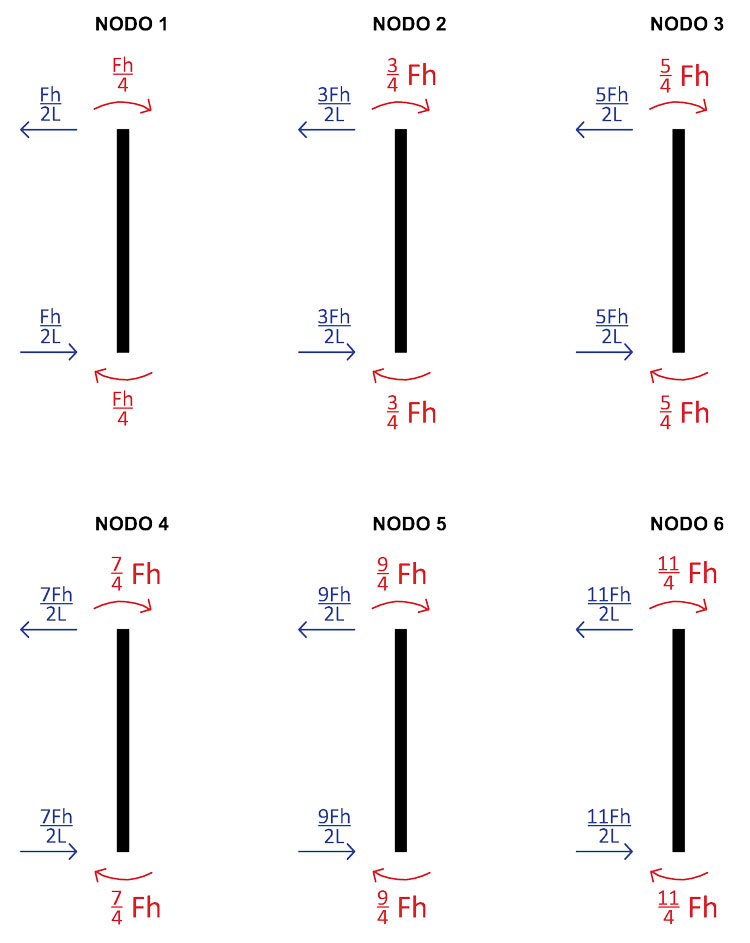
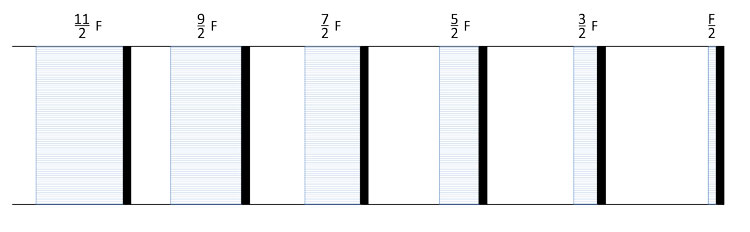
Grazie ai valori del taglio appena trovati, sappiamo anche quanto vale lo sforzo normale sui traversi, in quanto secondo il principio dell'equilibrio dei nodi ciò che è taglio diventa sforzo normale e viceversa. Il diagramma sarà perciò questo:

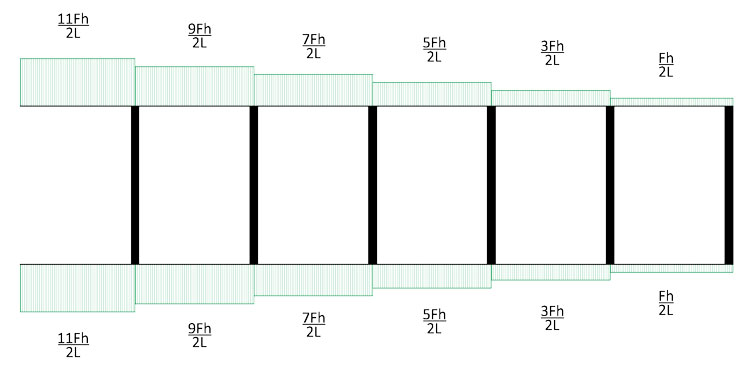
Come si nota dal diagramma, i traversi orizzontali sono tesi, mentre quelli inferiori sono compressi.

Ora non ci rimane che verificare la bontà del metodo utilizzato, disegnando su SAP2000 la nostra trave Vierendeel e ricordandoci di modificare il modulo elastico (E) del materiale che utilizzeremo per i pilastri verticali, assegnandogli un valore molto alto. Di seguito riporto i diagrammi di sforzo normale, taglio e momento e l'analisi della deformata:

SFORZO NORMALE

TAGLIO

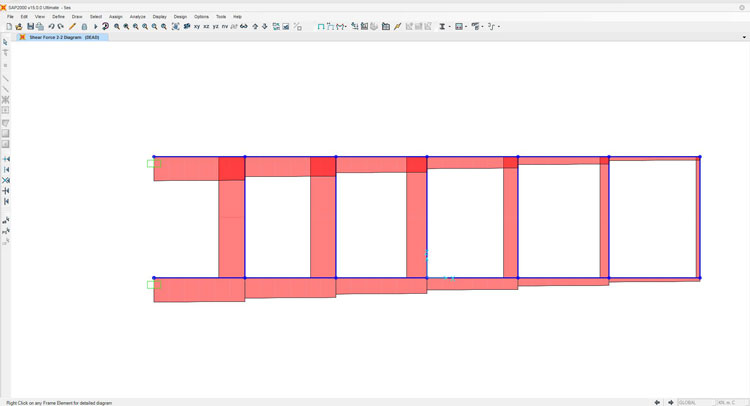
MOMENTO FLETTENTE

DEFORMATA