Esercitazione_2.1 trave reticolare piana (risoluzione a mano e tramite software SAP2000)

 

Esercitazione_2.1

trave reticolare piana (risoluzione a mano e tramite software SAP2000)

 

 

1_

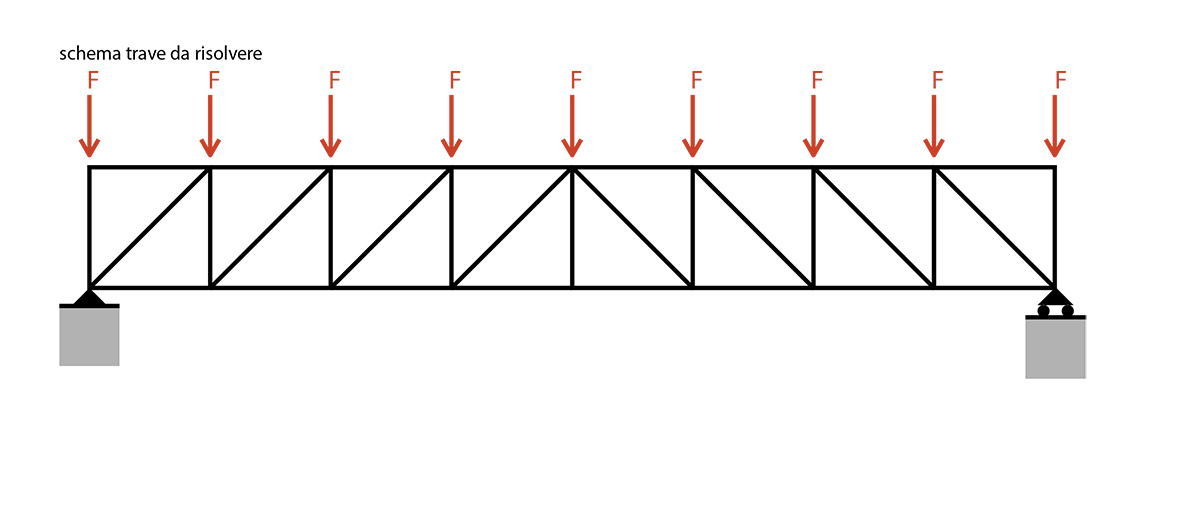
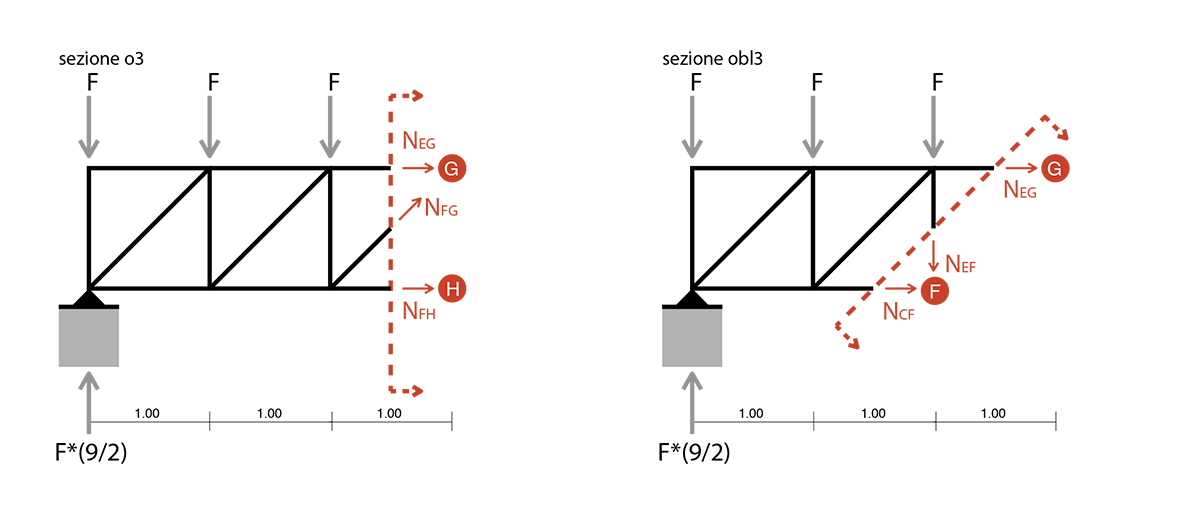
Il sistema proposto risulta essere un sistema isostatico, quindi per poterlo risolvere si ricorre ad uno schema equivalente di trave appoggiata-appoggiata per risolvere le reazioni vincolari e successivamente al metodo delle sezioni di Ritter per risoluzione delle aste della reticolare, quale metodo delle sezioni riesce a definire gli sforzi normali presenti sulle aste, definendo di conseguenza la loro natura di puntoni o tiranti.

 

 

2_

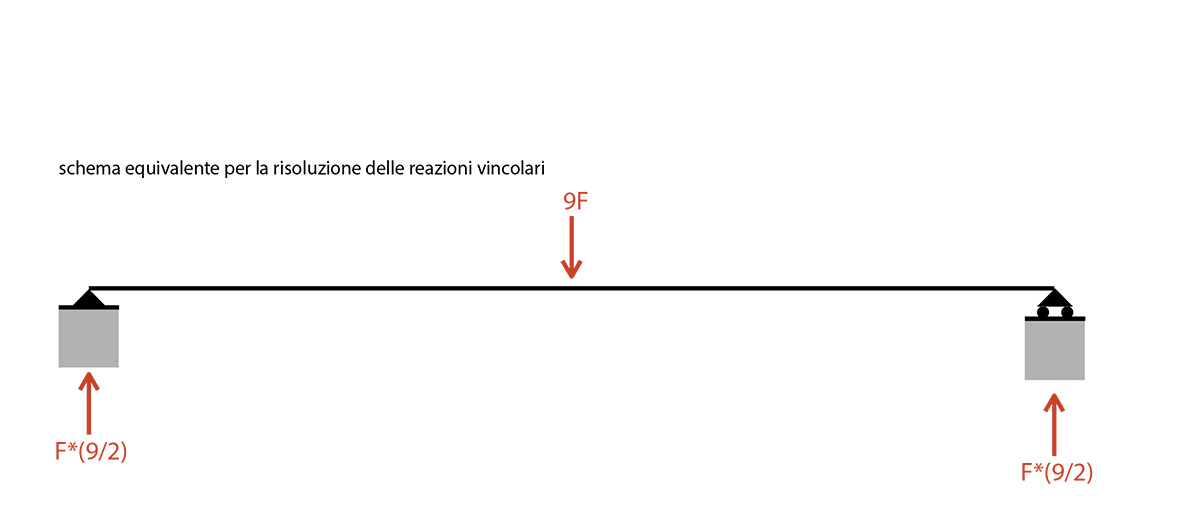
Si procede con la risoluzione di uno schema equivalente di trave appoggiata-appoggiata per definire le reazioni vincolari, nel caso dell’esercizio:

RUA = 0 

RVA + RVB - (9*F) = 0 ⇒ RVA = RVB = (1/2*(9*F))

 

 

3_

Si procede con l’applicazione del metodo delle sezioni di Ritter (metodo degli equilibri parziali), in questo metodo, la parte di struttura che deve essere in equilibrio viene individuata da una sezione che taglia le aste, dove le 3 aste tagliate non devono mai convergere nello stesso nodo. Questo metodo analizza le azioni di contatto presenti nelle aste andando a definire il loro sforzo normale e la loro classificazione (puntoni o tiranti).

 

 

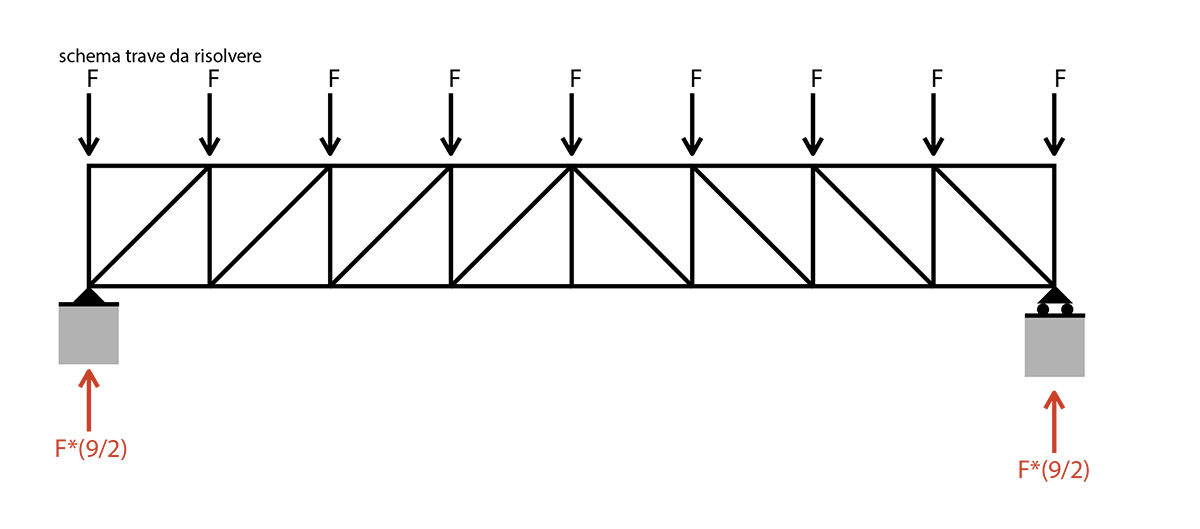
sezione verticale_1

 

Eql. alla rotazione

MD= F*L + NAC*L - (1/2*(9*F))*L = 0 => NAC = (1/2*(7*F)) _puntone

Eql. delle forze verticali

(√2/2)*NAD - F + (1/2*(9*F)) = 0 => (√2/2)*NAD  = -(1/2*(7*F))

=> NAD = -(1/√2*(7*F)) _tirante

Eql. delle forze orizzontali

NBD + (1/2*(7*F)) - (1/2*(7*F)) = 0 => NBD = 0 _scarica

sezione obliqua_1

 

Eql. delle forze verticali

NAB + (1/2*(9*F)) - (1/2*(7*F)) = 0 => NAB = -F _tirante

 

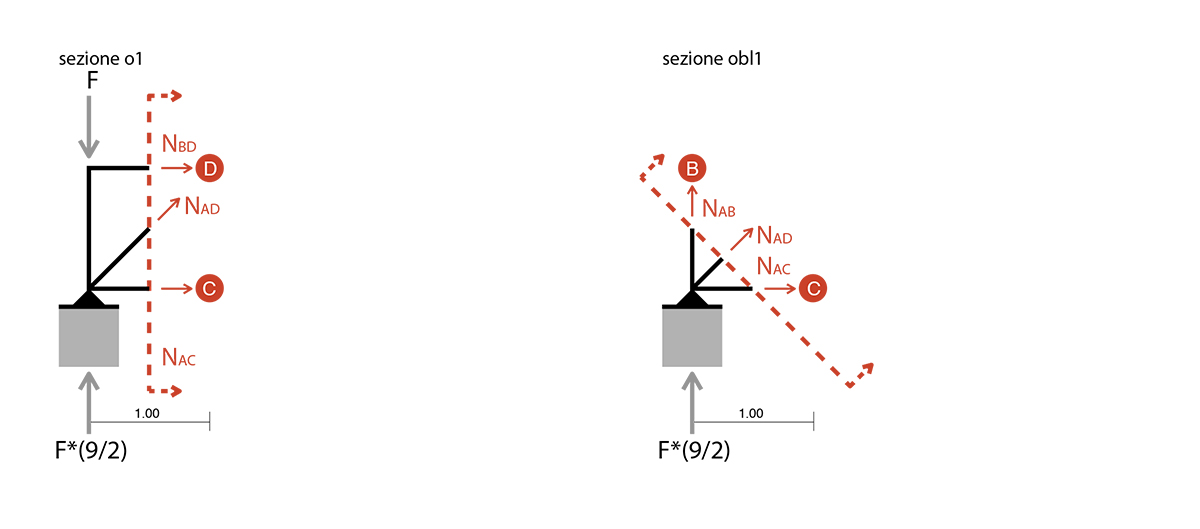
sezione verticale_2

 

Eql. alla rotazione

ME= F*L  + (2*(F*L))+ NCF*L - (1/2*(9*F))*(2*L) = 0 => NCF = (1/2*(3*F)) _puntone

Eql. delle forze verticali

(√2/2)*NCE - 2*F + (1/2*(9*F)) = 0 => (√2/2)*NCE  = -(1/2*(5*F))

=> NCE = -(1/√2*(5*F)) _tirante

Eql. delle forze orizzontali

NDE + (1/2*(3*F)) - (1/2*(5*F)) = 0 => NDE = F _puntone

sezione obliqua_2

 

Eql. delle forze verticali

- NDc + (1/2*(9*F)) - 2*F = 0 => NDC = - (1/2*(5*F)) _tirante

 

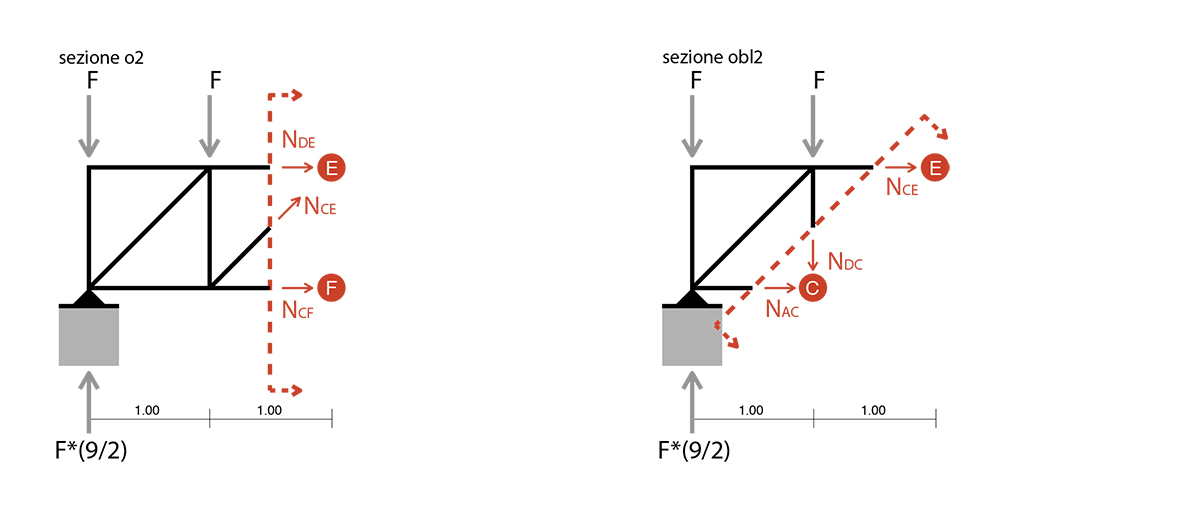
sezione verticale_3

 

Eql. alla rotazione

MD= F*L  + (2*(F*L)) + (3*(F*L)) + NFH*L - (1/2*(9*F))*(3*L) = 0 => NFH = (1/2*(15*F)) _puntone

Eql. delle forze verticali

(√2/2)*NFG - 3*F + (1/2*(9*F)) = 0 => (√2/2)*NCE  = -(1/2*(3*F))

=> NFG = -(1/√2*(3*F)) _tirante

Eql. delle forze orizzontali

NEG + (1/2*(15*F)) - (1/2*(3*F)) = 0 => NEG = 6*F _puntone

sezione obliqua_3

 

Eql. delle forze verticali

- NEF + (1/2*(9*F)) - 3*F = 0 => NEF = - (1/2*(3*F)) _tirante

 

sezione verticale_4

 

Eql. alla rotazione

MI= F*L  + (2*(F*L)) + (3*(F*L)) + (4*(F*L)) + NHJ*L - (1/2*(9*F))*(4*L) = 0

=> NHJ = 8*F _puntone

Eql. delle forze verticali

(√2/2)*NHI - 4*F + (1/2*(9*F)) = 0 => (√2/2)*NCE  = -(1/2*F)

=> NHI = -(1/√2**F) _tirante

Eql. delle forze orizzontali

NGI  + 8*F - (1/2**F)  = 0 => NGI = (1/2*(15*F)) _puntone

sezione obliqua_4

 

Eql. delle forze verticali

- NGH + (1/2*(9*F)) - 4*F = 0 => NGH = 1/2*F _puntone

 

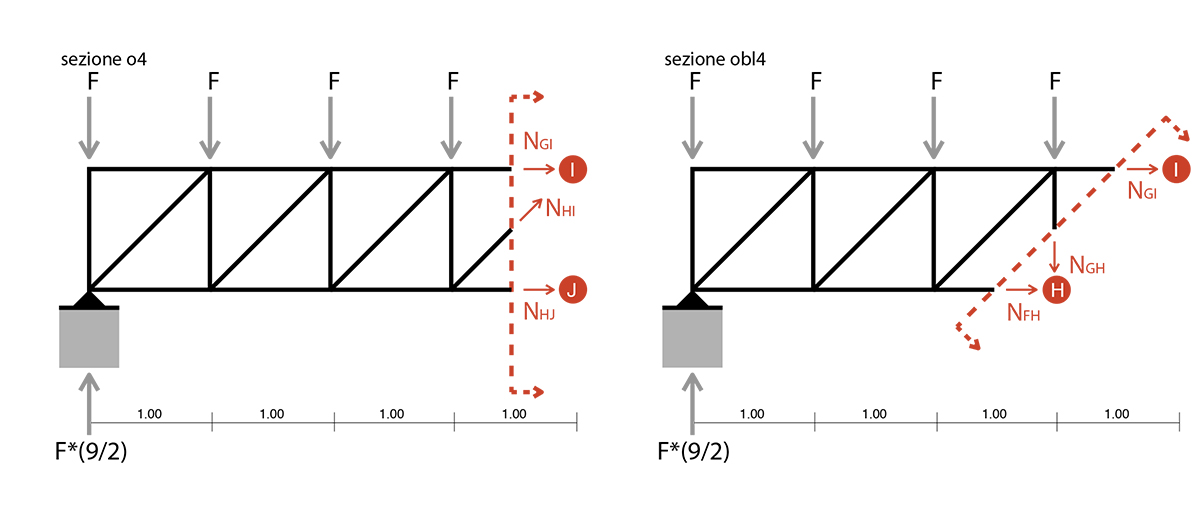
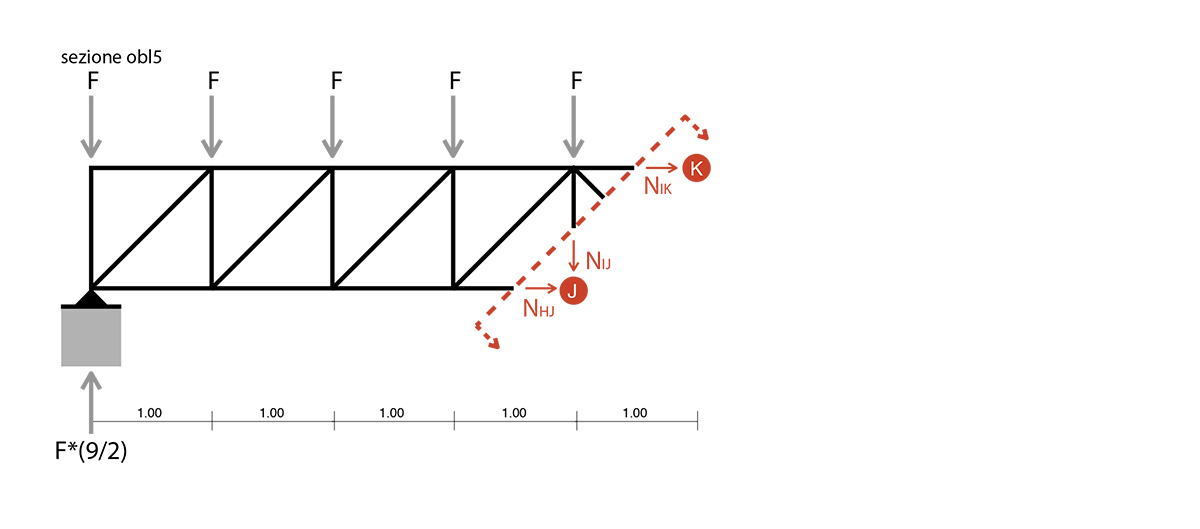
sezione obliqua_5

 

Eql. delle forze verticali

- NIJ + (1/2*(9*F)) - 5*F = 0 => Nij = - (1/2*(3*F)) _tirante

 

4_

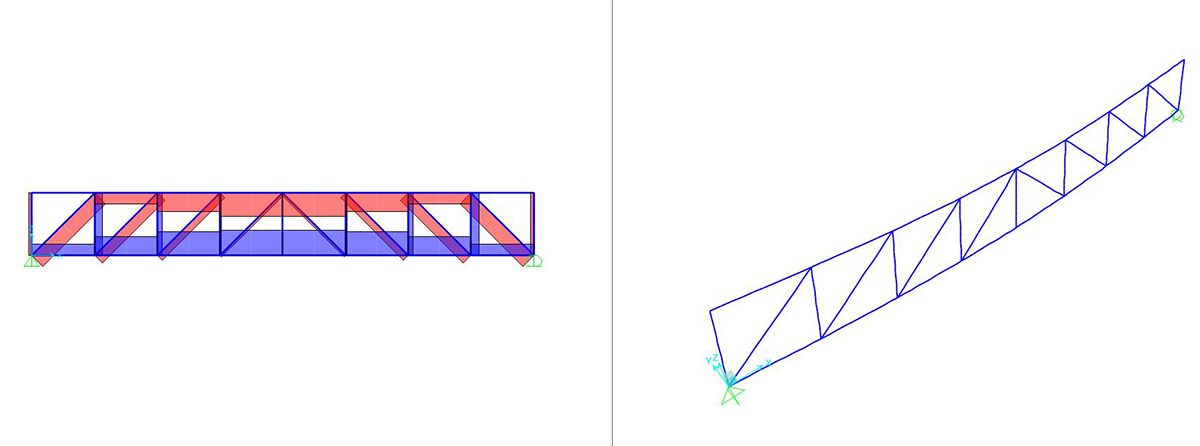
Successivamente alla risoluzione del sistema della trave reticolare si procede con la graficizzazione del diagramma dei sforzi normali delle aste, come si può vedere in fingura:

 

 

 

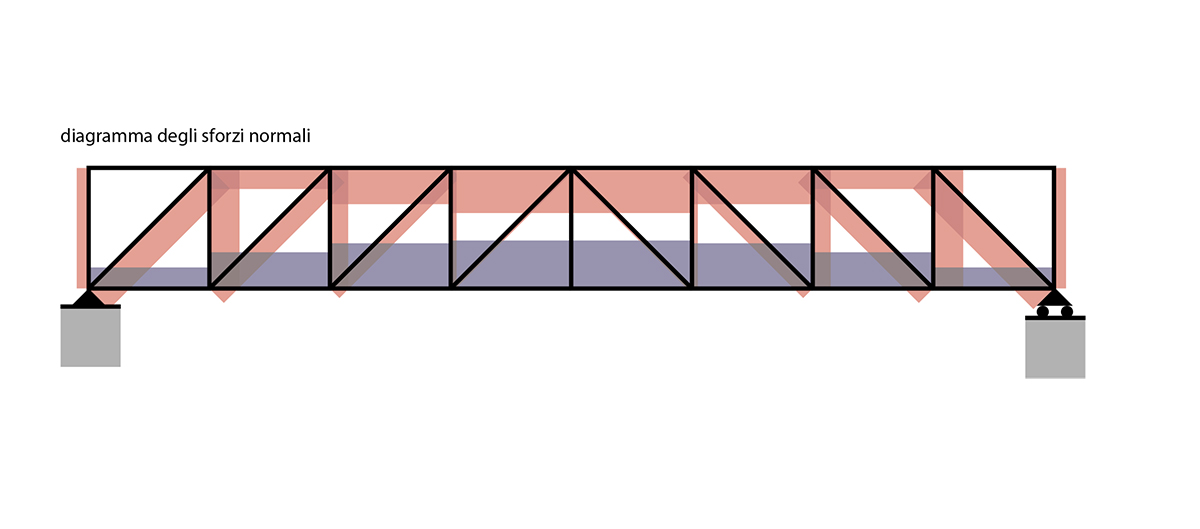
5_

Successivamente alla risoluzione a mano del sistema della trave reticolare si procede con la verifica tramite il software SAP.

La modellazione viene effettuata per comodità direttamente in SAP.

creare un nuovo file con una griglia utile al disegno dell’asta:

FILE > NEW MODEL >

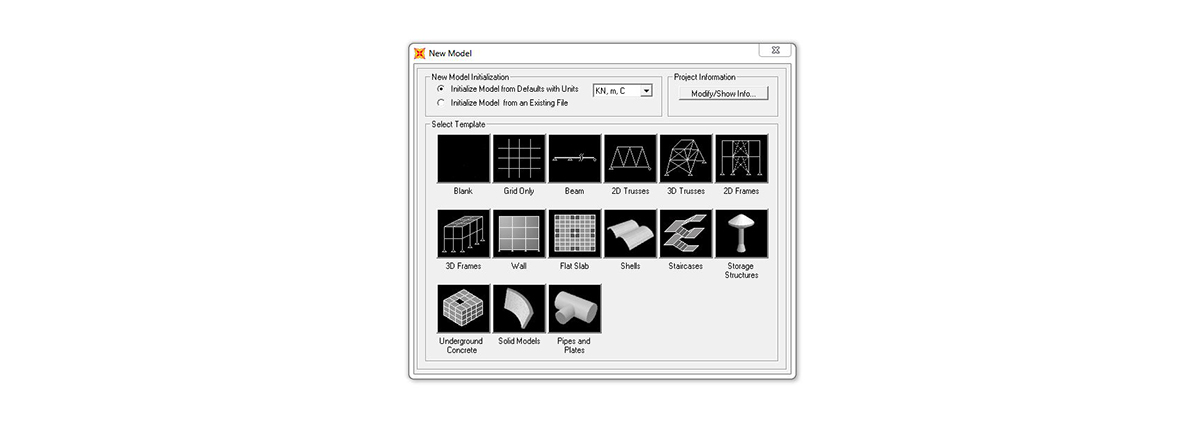
QUICK GRID LINES > impostare 9 assi sull’asse x, 1 sull’asse y e 2 sull’asse z > impostare come GRID SPACING la dimensione che vorremo dare alla lunghezza della trave

 

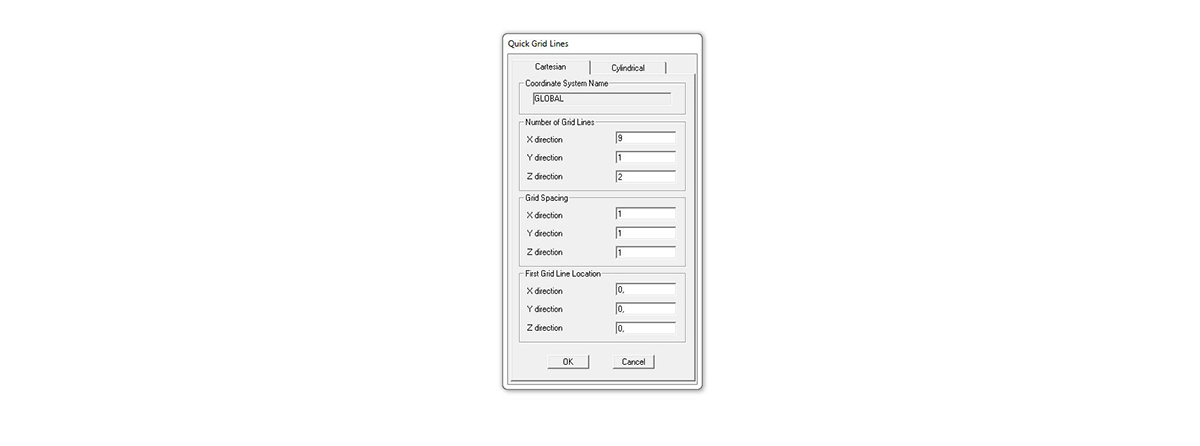
le impostazioni date alla griglia dovrebbero produrre una condizione analoga alla seguente:

 

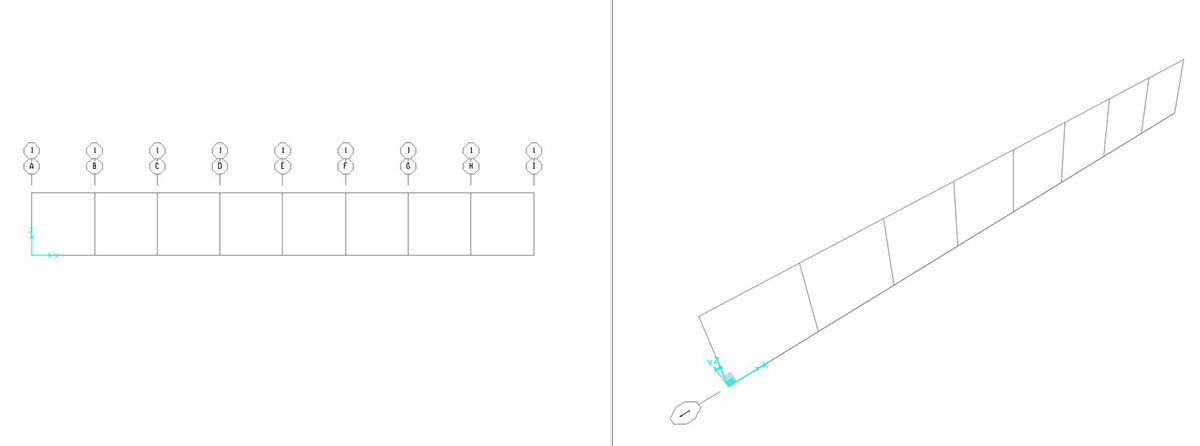
disegnare le aste della trave seguendo la spaziatura della griglia preimpostata.

 

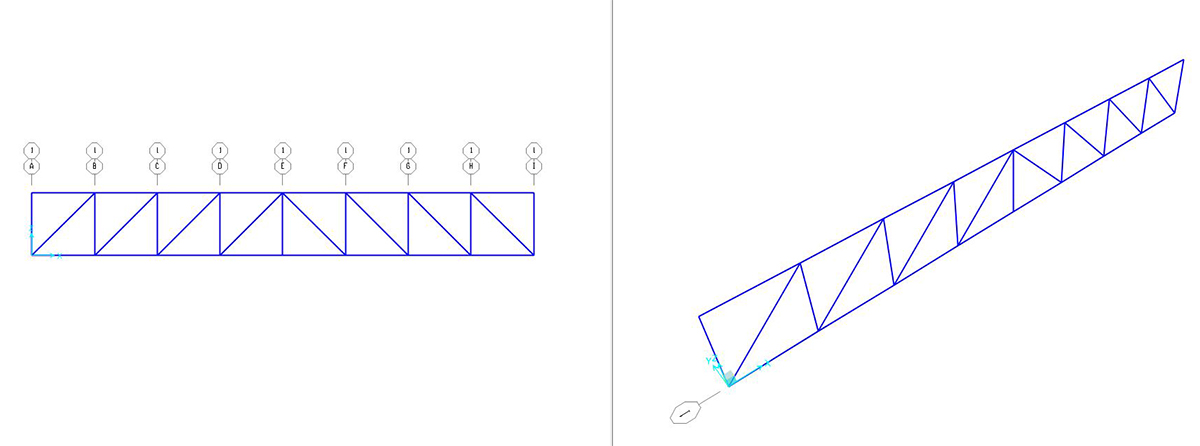
assegnare i vincoli: 

selezionare il punto > ASSIGN > JOINT RESTRAINTS > spuntare le sollecitazioni che il vincolo da posizionare trattiene

 

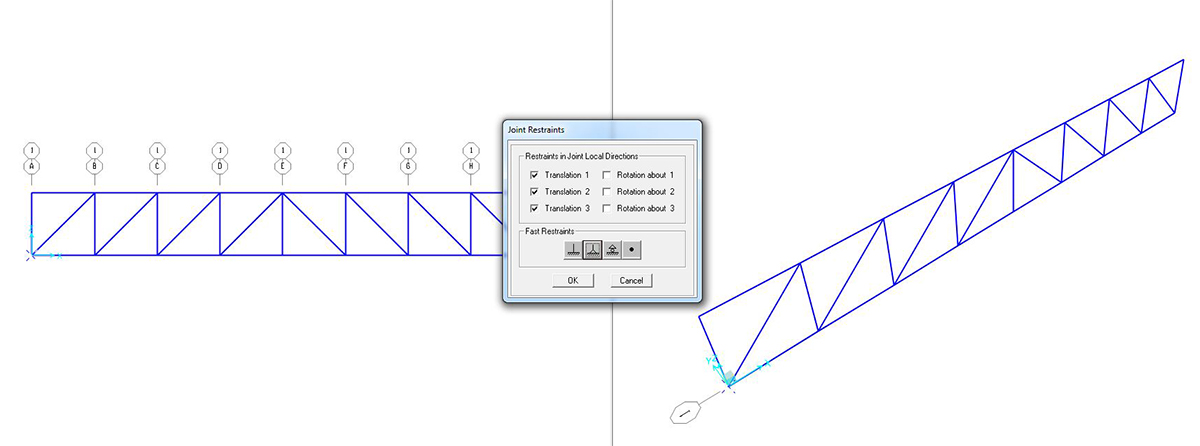
assegnare un incastro a sinistra ed un carrello a destra

 

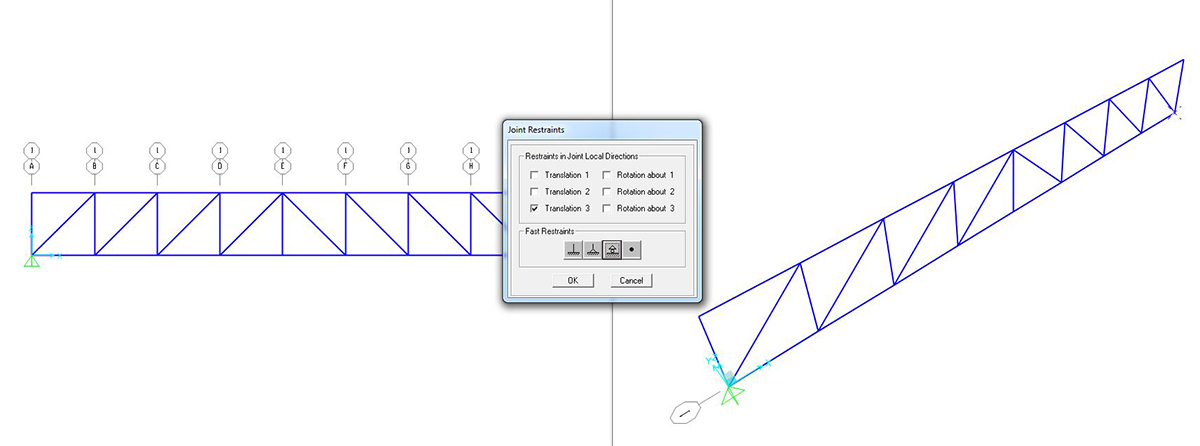
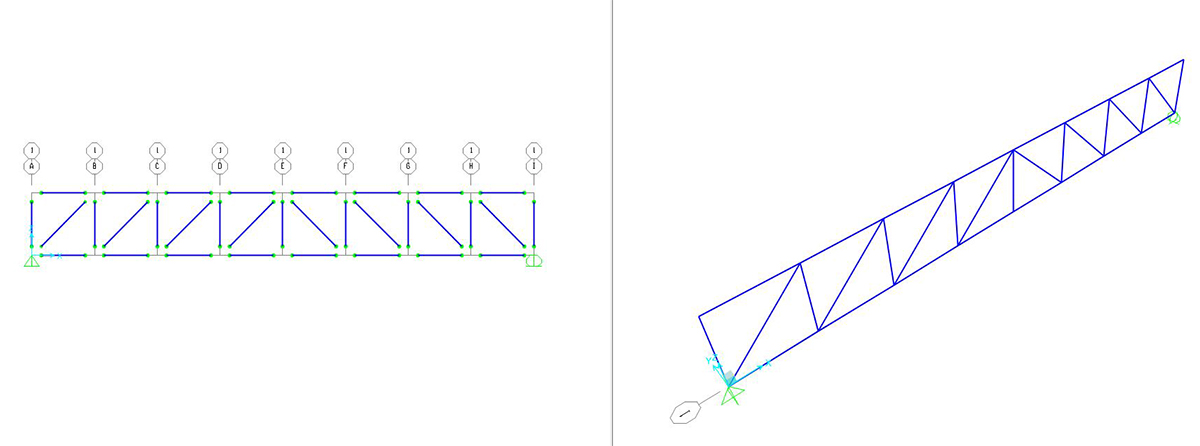
Dato che in una struttura reticolare tutti i vincoli interni sono cerniere, dobbiamo fare un’operazione di rilascio del momento ASSIGN > FRAME > RELEASE > MOMENT 3-3(MAJOR) > START 0 – END 0.

 

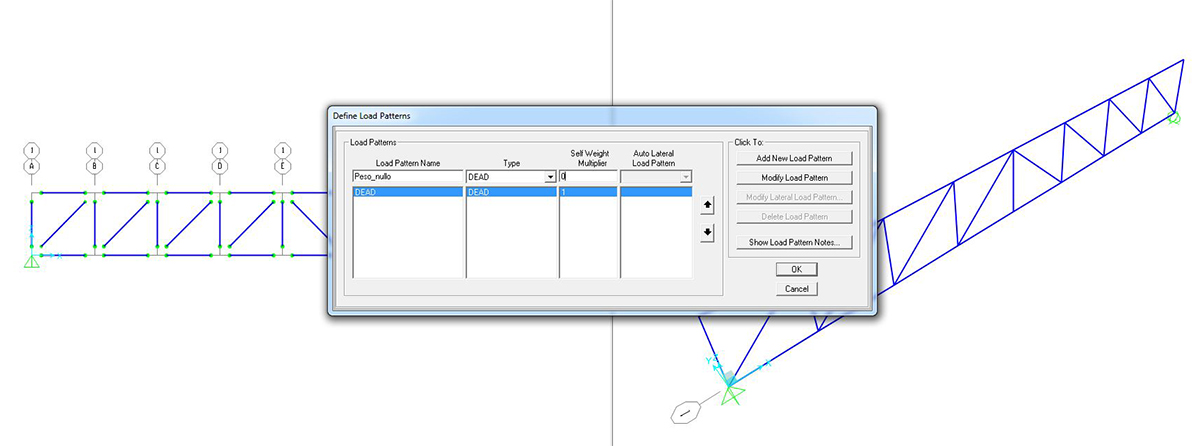
N.B. In questo tipo di esercizi, impostiamo l’analisi in modo che non consideri il peso proprio della struttura (che costituirebbe un carico distribuito su travi che si deve considerare scariche). 

Ciò viene fatto creando un nuovo LOAD PATTERN che abbia 0 come coefficiente di moltiplicazione del carico SELF WEIGHT MULTIPLER.

 

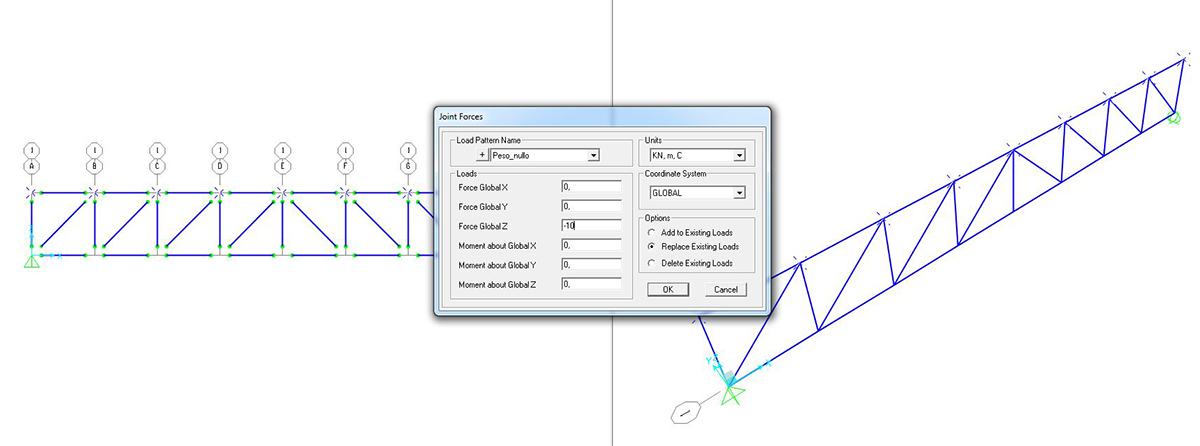
Si procede con l’assegnazione dei carichi con il comando ASSIGN > JOINT LOADS > FORCES, trattandosi di un’idealizzazione per la quale i carichi sono concentrati tutti nei nodi.

 

N.B. si possono anche analizzare gli sforzi a cui sono sottoposti i vincoli dando il comando SHOW FORCES/STRESSES > JOINTS.

 

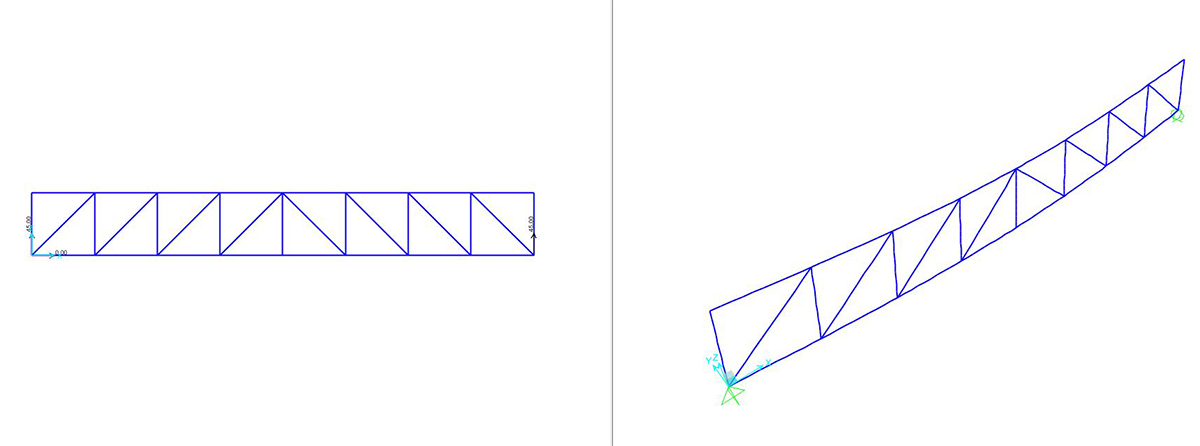
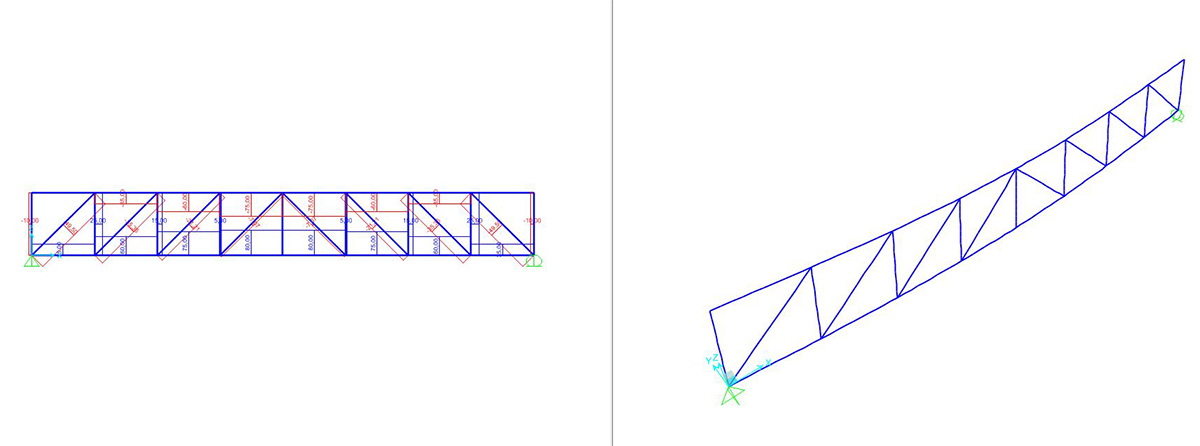
Possiamo ora avviare l’analisi. Il software mostra per prima cosa l’andamento della deformata.

 

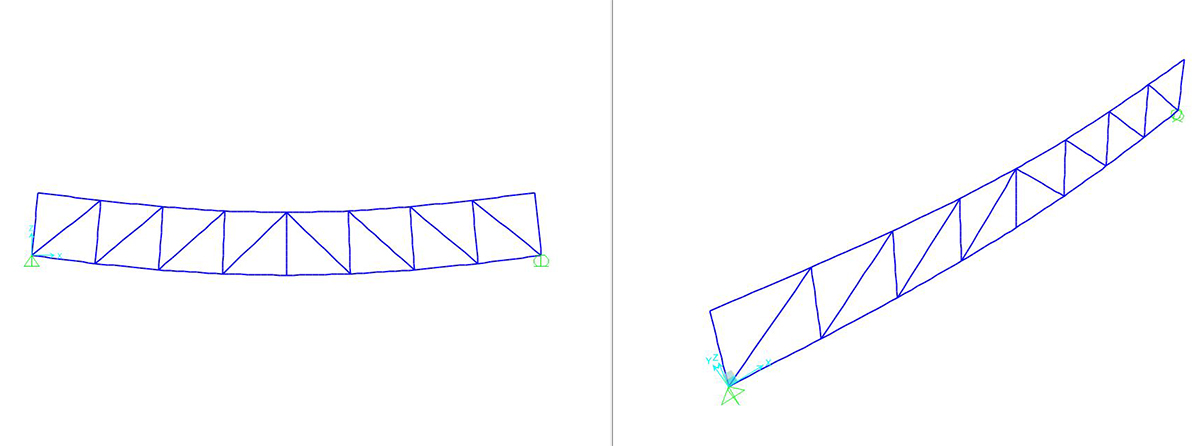
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > AXIAL FORCE