RIGIDEZZA TORSIONALE

In questo esercizio si vuole capire come influisce la torsione in un sistema strutturale . Analizzeremo una struttura tridimensionale e vedremo come il momento agente sul nodo si ripartisce in parte in momento flettente e in parte in momento torcente. 

SCHEMA DI CALCOLO

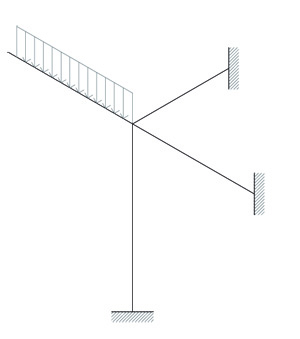
La mensola è soggetta al carico distribuito che posso  sostituire , essendo un tratto isostatico in un contesto iperstatico, con il corrispondente valore del momento flettente applicato nel nodo. La struttura si trova in uno spazio tridimensionale presenta dunque sei gradi di libertà. poichè le aste sono indeformabile assialmente avremo che ux, uy, uz saranno uguale a zero.

Quello che agisce sulla struttura è un momento ql²/2 che provoca una rotazione. Il momento oltre a far ruotare le aste lungo xz provoca un momento torcente sull'asta perpendicolare.

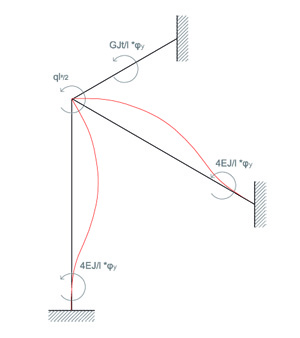
Il problema presenta un’incognita la rotazione che sarà trovata scrivendo l’equilibrio contro la rotazione del nodo:

ql²/2 = φy ( 4EI/l1 + 4EI/l2 + GJT/l3)

dove ( 4EI/l1 + 4EI/l2 + GJT/l3) = Rn ⇒RIGIDEZZA DEL NODO 

Ora svolgeremo l'esercizio in SAP trovandoci i valori di sollecitazioni delle varie aste e lo faremo cambiando di volta in volta sezioni e materiali per vederne come reagiscono le aste a seconda del materiale (acciaio e calcestruzzo) . 

Ricordiamo che  per una generica sezione il momento torsionale vale:

MT = (G*JT/l) ϑ(l)

dove:

G = modulo di elasticità tangenziale (dipende dal materiale)

Calcestruzzo:  Gcls = 10⁷ KN/m²

Acciaio: Gsteel = 8*10⁷ kN/m²

JT = momento di inerzia polare (dipende dalla sezione)

ϑ(l) = angolo unitario di rotazione

(G*JT/l) rappresenta la rigidezza torsionale delle generica asta di lunghezza "l".

Definiamo ora il carico e le luci delle aste

q = 10kN/m

l = 2m

My = ql²/2 = 20 kN/m

Calcestruzzo

• Sezione rettangolare 

Jt = c₂ * ab³

è tabelleto in funzione di a/b . In questo caso c2 = 0,291

Jt = (0,291) 0,63 * (0,15)³ = 0,0006475 m³

ql²/2 = φ ( 4EI/l1 + 4EI/l2 + GJt/l3)

E (modulo di elasticità) = 21000000 kN/m²

I (momento di inerzia) = bh³/12 

G = 10000000 kN/m²

Rn = ( 4EI/l1 + 4EI/l2 + GJt/l3) 

φy = ql²/2 / Rn 

Svolgiamo ora l'esercizio in SAP assegnando alle aste una sezione rettangolare piena in cls armato e applichiamo il momento agente lungo l'asse y

                                  deformata                                                                momento ( -9,30)

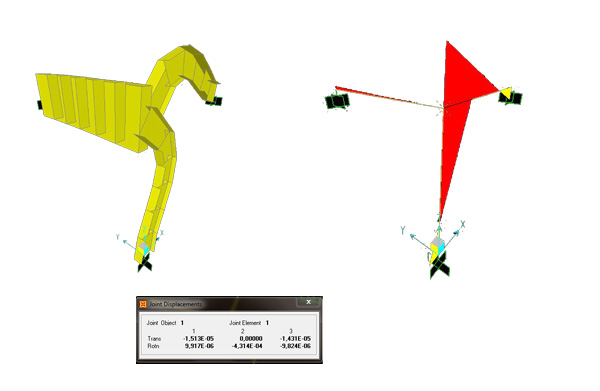
φy= 0,0004314  

• Sezione circolare 

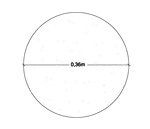
I (momento di inerzia) = pgreco*r⁴ /64 = 0,008245 m⁴

Jp = momento polare di inerzia = pgrego r⁴/ 2 = 0,00164 m³

Rn = ( 4EI/l1 + 4EI/l2 + GJp/l3)

φy = ql²/2 / Rn 

                          deformata                                                                momento ( -8,35)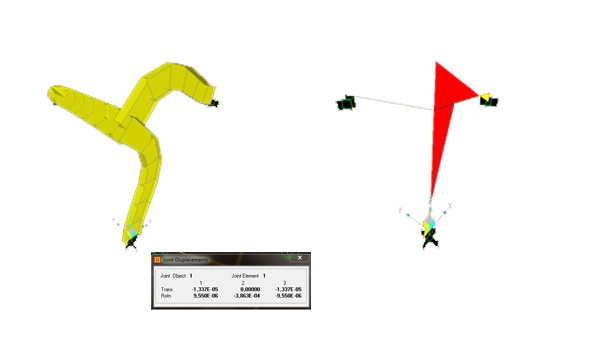                   

φy= 0,0003863

Acciaio

•  Sezione quadrata cava

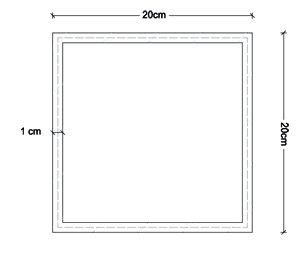
Jt = 4Ω²t/ lm = 0,00006859 m²

Rn= ( 4EI/l1 + 4EI/l2 + GJt/l3)

φy = ql²/2 / Rn 

                           deformata                                                                momento ( -9,85)  

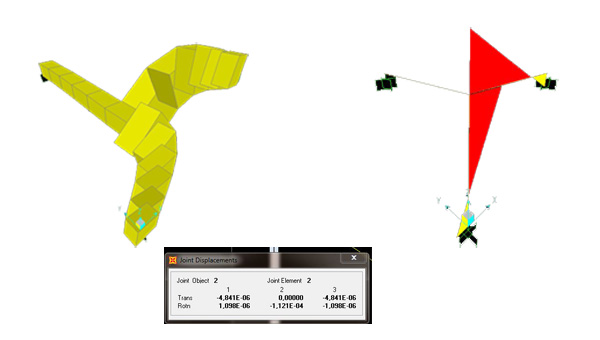
φy = 0,0001121

• Ipe

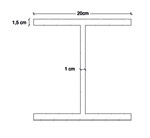
E (modulo di elasticità) = 21000000 kN/m²

G (modulo di elasticità tangenziale) = 80000000 kN/m²

Jt  = 0,0000004833 m³

Rn= ( 4EI/l1 + 4EI/l2 + GJt/l3)

φy = ql²/2 / Rn 

                      deformata                                                                momento ( -9,99)  

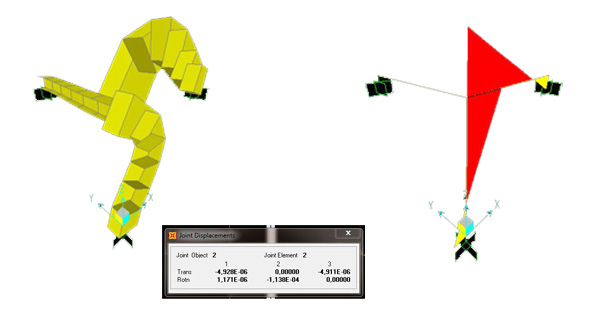
φy = 0,0001138

Dai risultati ottenuti si può notare che le sezioni in acciaio offrono una maggiore resistenza rispetto a quelle in calcestruzzo in quanto possiedono un modulo di elasticità tangenziale superiore. Tra le sezioni in acciaio quella che risulta avere una migliore rigidezza torsionale è il profilo chiuso cavo, in quanto le tensioni tangenziali aumentano all'aumentare della loro distanza torsionale.