blog di valentina.liguori

In questo esercizio studieremo il comportamento di due travi perpendicolari tra di loro , le quali collaborano tra di loro per garantire un miglior equilibrio alla struttura.

SCHEMA DI RIFERIMENTO

DEFORMATA

Lungo l'asta 2 avendo la forza che cade perfettamente al centro si avrà come detto precedentemento solo abbassamento, sull'asta 1 invece, abbiamo in y anche la rotazione poichè la forza non cade perfettamente al centro, ma a 1/3L .

Dunque  per quanto riguarda gli spostamenti sappiamo che u_x = 0 , u_y = 0 e u_z = δ ; per quanto riguarda le rotazioni abbiamo solo φ_Y. 

          

        

       

FL²/EI - δ/L*(1113/2) + 81/2  φ_Y = 0

 

Vado ora a sostituire δ/L con l'equazione prima ottenuta

 

FL²/EI - 1113/2*[(36+8α)/81]φ_Y+ 81/2  φ_Y = 0

FL²/EI - 371/27*(18+4α)φ_Y+ 81/2  φ_Y = 0

FL²/EI = 371/27*(18+4α)φ_Y+ 81/2  φ_Y = 0

 

Metto φ_Y in evidenza

 

φ_Y[371/27*18 -81/2 + 371/27 * 4α ] = 0 

φ_Y[1241/6 + 1484/27 α ] = 0 

FL²/EI = φ_Y[1241/6 + 1484/27 α ]

 

φ_Y = FL²/EI [1241/6 + 1484/27 α ]

 

Abbiamo così ottenuto φ_{Y e} δ 

 

Definiamo ora una sezione inserendo dei valori noti per trovare i valori incogniti della rotazione e dello spostamento .

 

Supponiamo di realizzare una struttura in cls , in cui entrambe le aste abbiano la seguente sezione :

 

 

                                         

supponiamo di avere una luce di 8m e una forza applicata pari a 40kN

 

Sappiamo che :

 

Jt  ( coefficiente di resistenza a torsione)

c₂ è tabelleto in funzione di a/b . In questo caso vale  a/b = 0.67/0.15= 4,46 →c2 = 0,291

Jt = c₂ab^{3 =} (0,291) 0,67 * (0,15)³ = 0,000658 m³

E (modulo di elasticità) = 21000000 kN/m²

I (momento di inerzia) = bh³/12 = (0,15 * 0,67³) /12 = 0,003759 m⁴

G ( modulo di elasticità tangenziale) = 10000000 kN/m²

Andiamo ora a sostituire i valori noti nell'equazioni prima trovate 

Ricordiamo che :

δ/L = (36 + 8α)/81φ_Y

φ_Y = FL²/EI [1241/6 + 1484/27 α ]

α = GJt/EI = 10000000 * 0,000658 / 21000000 * 0,003759 = 0,083355

φ_Y   =  40 * 64 / 21000000 * 0,003759 [ (1241/6 + 1484/27) * 0,08355] = 0,0001534

δ/L =  [(36 + 8 * 0,08355) / 81) * 0,0001534 = 0,0000808 

δ = 8 * 0,0000808 = 0,000646

VERIFICA SAP

Disegno la struttura grazie all'aiuto della griglia. Assegno i vincoli e la forza esterna, e cambio i valori del modulo di elasticità E e del modulo di elasticità tangenziale G. 

        

Assegno poi ad entrambe le travi la sezione scelta e faccio partire l'analisi. 

     

Leggiamo ora i risultati ottenuti. 

     

Abbiamo che Ux e Uy sono uguali a zero, mentre Uz = 0,0006524. Mentre per quanto riguarda la rotazione abbiamo un valore corrispondente a = 0,00008.

I valori trovati manualmente corrispondo, se non per un minimo scarto, a quelli trovati in sap. 

 

 

 

 

In questo esercizio si vuole capire come influisce la torsione in un sistema strutturale . Analizzeremo una struttura tridimensionale e vedremo come il momento agente sul nodo si ripartisce in parte in momento flettente e in parte in momento torcente. 

SCHEMA DI CALCOLO

La mensola è soggetta al carico distribuito che posso  sostituire , essendo un tratto isostatico in un contesto iperstatico, con il corrispondente valore del momento flettente applicato nel nodo. La struttura si trova in uno spazio tridimensionale presenta dunque sei gradi di libertà. poichè le aste sono indeformabile assialmente avremo che ux, uy, uz saranno uguale a zero.

Quello che agisce sulla struttura è un momento ql²/2 che provoca una rotazione. Il momento oltre a far ruotare le aste lungo xz provoca un momento torcente sull'asta perpendicolare.

Il problema presenta un’incognita la rotazione che sarà trovata scrivendo l’equilibrio contro la rotazione del nodo:

ql²/2 = φy ( 4EI/l1 + 4EI/l2 + GJT/l3)

dove ( 4EI/l1 + 4EI/l2 + GJT/l3) = Rn ⇒RIGIDEZZA DEL NODO 

Ora svolgeremo l'esercizio in SAP trovandoci i valori di sollecitazioni delle varie aste e lo faremo cambiando di volta in volta sezioni e materiali per vederne come reagiscono le aste a seconda del materiale (acciaio e calcestruzzo) . 

Ricordiamo che  per una generica sezione il momento torsionale vale:

MT = (G*JT/l) ϑ(l)

dove:

G = modulo di elasticità tangenziale (dipende dal materiale)

Calcestruzzo:  Gcls = 10⁷ KN/m²

Acciaio: Gsteel = 8*10⁷ kN/m²

JT = momento di inerzia polare (dipende dalla sezione)

ϑ(l) = angolo unitario di rotazione

(G*JT/l) rappresenta la rigidezza torsionale delle generica asta di lunghezza "l".

Definiamo ora il carico e le luci delle aste

q = 10kN/m

l = 2m

My = ql²/2 = 20 kN/m

Calcestruzzo

• Sezione rettangolare 

Jt = c₂ * ab³

è tabelleto in funzione di a/b . In questo caso c2 = 0,291

Jt = (0,291) 0,63 * (0,15)³ = 0,0006475 m³

ql²/2 = φ ( 4EI/l1 + 4EI/l2 + GJt/l3)

E (modulo di elasticità) = 21000000 kN/m²

I (momento di inerzia) = bh³/12 

G = 10000000 kN/m²

Rn = ( 4EI/l1 + 4EI/l2 + GJt/l3) 

φy = ql²/2 / Rn 

Svolgiamo ora l'esercizio in SAP assegnando alle aste una sezione rettangolare piena in cls armato e applichiamo il momento agente lungo l'asse y

                                  deformata                                                                momento ( -9,30)

φy= 0,0004314  

• Sezione circolare 

I (momento di inerzia) = pgreco*r⁴ /64 = 0,008245 m⁴

Jp = momento polare di inerzia = pgrego r⁴/ 2 = 0,00164 m³

Rn = ( 4EI/l1 + 4EI/l2 + GJp/l3)

φy = ql²/2 / Rn 

                          deformata                                                                momento ( -8,35)                   

φy= 0,0003863

Acciaio

•  Sezione quadrata cava

Jt = 4Ω²t/ lm = 0,00006859 m²

Rn= ( 4EI/l1 + 4EI/l2 + GJt/l3)

φy = ql²/2 / Rn 

                           deformata                                                                momento ( -9,85)  

φy = 0,0001121

• Ipe

E (modulo di elasticità) = 21000000 kN/m²

G (modulo di elasticità tangenziale) = 80000000 kN/m²

Jt  = 0,0000004833 m³

Rn= ( 4EI/l1 + 4EI/l2 + GJt/l3)

φy = ql²/2 / Rn 

                      deformata                                                                momento ( -9,99)  

φy = 0,0001138

Dai risultati ottenuti si può notare che le sezioni in acciaio offrono una maggiore resistenza rispetto a quelle in calcestruzzo in quanto possiedono un modulo di elasticità tangenziale superiore. Tra le sezioni in acciaio quella che risulta avere una migliore rigidezza torsionale è il profilo chiuso cavo, in quanto le tensioni tangenziali aumentano all'aumentare della loro distanza torsionale.

Si vuole, nella seguente esercitazione, analizzare come un impalcato reagisce a forze orizzontali tramite l'azione dei controventi.

IMPALCATO DI RIFERIMENTO - piano tipo in c.a. -

L'impalcato presenta due diverse orditure di solaio. Abbiamo pilastri di forma rettangolare, le cui dimentsioni sono le seguenti :

I controventi presentano un'elasticità che ci permette di considerarli cedevoli. Possono dunque essere semplificati con delle molle.

Verifichiamo l'efficacia dei controventi analizzando le loro rigidezze. Per farlo, occorre trovare il centro delle rigidezze e ripartire le forze orizzontali. Analizziamo il calcolo utilizzando un foglio excel.

STEP 1 : Calcolo delle rigidezze traslanti e dei controventi dell'edificio

Inserendo i seguenti dati nella tabella :

• modulo di elasticità del Cls E=21000 N/mm²;
• momento d'inerzia di ciascun pilastro ;
• altezza dei pilastri (320 cm);

possiamo calcolare qual'è la rigidezza che i vari telai oppongono alla translazione lungo i loro assi.

STEP 2 : Tabella sinottica controventi e distanze

Vengono riportate le distanze verticali e orizzontali dei telai dal punto di origine O

STEP 3 : Calcolo del centro di massa

Semplificando l'impalcato in forme semplici (rettangoli) , mi calcolo facilmente l'area di ogni rettangolo e calcolo il centro di massa facendo la somma delle cordinate lungo gli assi x e y, per l'area di ogni rettangolo suddiviso, diviso l'area totale.

STEP 4 : Calcolo del centro di rigidezze e delle rigidezze globali

Il centro delle rigidezze è il centro del sistema di forze considerate, in cui viene applicata la risultante delle rigidezze traslanti dei controventi lungo l’asse x ed y. Nella tabella vengono indicate le distanze di ogni telaio dal centro di rigidezza e la rigidezza torsionale Kϕ, che è la rigidezza a rotazione di tutte le molle.      

STEP 5 : Analisi dei carichi sismici

Vieni ora definita la forza sismica, applicata nel centro di massa. La somma del carico permanente totale e del carico totale accidentale , moltiplicata per il coefficiente di contemporaneità, ci dà il valore dei pesi sismici che divisi per il coefficiente di intensità sismica, ci danno il valore della forza sismica orizzontale.

STEP 6 - 7 : Ripartizione della forza sismica lungo x e y

Possiamo ora analizzare come si ripartisce la forza sismica lungo gli assi x e y per ognuno dei controventi; trovando il momento torcente , moltiplicando la forza sismica per il suo braccio. Calcoliamo poi la traslazione orizzontale, dividendo la forza F per la rigidezza traslante orizzontale, e la traslazione verticale, dividendo la forza F  per la rigidezza traslante verticale, e le rotazioni, dividendo i momenti torcenti, lungo x e y, per la rigidezza rotazionale.

Ripartizione della forza lungo l'asse x

Ripartizione della forza lungo l'asse y

Esercizio 1 : TRAVE VIERENDEEL

 SCHEMA DI CALCOLO

Riferendoci allo schema notevole riportato di seguito, conoscendo il valore di δ possiamo determinare il valore delle caratteristiche di sollecitazione e delle rigidezze dei traversi :

Determiniamo il valore del taglio e del momento nei vari tratti della struttura :

DIAGRAMMA DEL TAGLIO        

DIAGRAMMA MOMENTO

EQUILIBRIO AI NODI -MOMENTO -

EQUILIBRIO SULLE ASTE RIGIDE - TAGLIO -

DIAGRAMMA DEL TAGLIO

DIAGRAMMA DEL MOMENTO

VERIFICA SAP2000

DIAGRAMMA TAGLIO

DIAGRAMMA MOMENTO

Esercizio 2 : TRAVE DOPPIAMENTE INCASTRATA

SCHEMA DI CALCOLO

La trave è simmetrica e simmetricamente caricata, quindi ne basta studiare metà. In corrispondenza della simmetria la forza F  diverrà F/2.

Determiniamo il valore del taglio e del momento nei vari tratti della struttura :

DIAGRAMMA DEL TAGLIO

DIAGRAMMA DEL MOMENTO

EQUILIBRIO AI NODI -MOMENTO -

EQUILIBRIO SULLE ASTE RIGIDE - TAGLIO -

DIAGRAMMA DEL TAGLIO

DIAGRAMMA DEL MOMENTO

VERIFICA SAP2000

DIAGRAMMA SFORZO ASSIALE

DIAGRAMMA DEL TAGLIO

DIAGRAMMA DEL MOMENTO

In questa esercitazione ci troviamo a risolvere una struttura iperstarica con il metodo delle forze. Il metodo delle forze consiste nel porre come incognite del problema alcune reazioni vincolari, il cui numero è pari al grado di iperstaticità della struttura presa in esame.

SCHEMA DI RIFERIMENTO

SCHEMA ISOSTATICO EQUIVALENTE - Trasformo le cerniere in C, B, D in cerniere interne, in modo da rompere la continuità della trave , abbassando i gradi di vincoli da tre a due. 

EQUAZIONI DI COMPATIBILITA' CINEMATICA

Impongo che ∆φ = 0 ossia che la rotazione in corrispondenza degli appoggi sia uguale a zero e mi ricavo i valori dovuti a x e al carico in base ai seguenti schemi notevoli :

Punto B

∆φB = φBs – φBd = 0

φBs = φBs (q) + φBs (X₁) =  ql³/24EI – X₁L / 3EI

φBd = φBd (q) + φBd (X₁) + φBd (X₂) = - ql³/24EI + X₁L/3EI + X₂L/6EI

ql³/24EI – X1L / 3EI – (- ql³/24EI + X₁L/3EI + X₂L/6EI) = 0    

1. X₂= - 4 X₁+ ql²/2

Punto C

∆φC = φCs – φCd = 0

φCs = φCs (q) + φCs (X₁) + φCs (X₂) =  ql³/24EI – X₁L / 6EI – X₂L / 3EI

φCd = φCd (q) + φCd (X₁) + φCd (X₂) = - ql³/24EI + X₁L/6EI + X₂L/3EI

ql³/24EI – X₁L / 6EI – X₂L / 3EI – (- ql³/24EI + X₁L/6EI + X₂L/3EI) = 0  

1. X₁= - 2 X₂+ ql²/4

Metto a sistema le due equazioni ( 1 e 2 ) e mi ricavo le incognite X₁ e X₂ per sostituzione

X1= 3/28 ql²

 X2= 1/14 ql²

REAZIONI VINCOLARI 

- In relazione al carico

Per il principio di sovrapposizione degli effetti avremo :

In relazione ai momenti X₁ e X₂ :

Ne ricavo che 

Per il principio di sovrapposizione degli effetti ( carico + momento) avremo :

DIAGRAMMA DEL TAGLIO

asta 1 :

T(s) = -11/28 ql + qs 

T(s=0) = -11/28ql

T(s=l) = -11/28ql + ql = 17/28 ql

asta 2

T(s) = -11/28ql - 8/7ql + qs

T(s=0) = -11/28ql - 8/7ql + ql = -15/28 ql

T (s=2l) = -11/28 ql - 8/7ql + 2ql = 13/28ql

asta 3

T(s) = -11/28 ql - 8/7ql - 13/14ql + qs 

T(s=2l) = -11/28ql - 8/7ql + 2ql = -13/28 ql

DIAGRAMMA DEL MOMENTO

asta 1 :

M(s) = qs²/2 + 11/28qls + 8/7ql (s-l)

M(s=0) = 0

M(s=2l) = -2ql²/2 + 11/28ql² + 8/7ql²= -ql

Mmax ⇒ T=0 ⇒ s = 11/28l

M(s= 11/28l) = -[q(11/28l)2]/2 + 11/28ql (11/28l) = 121 / 1568ql²

asta 2 

M(s) = -qs²/2 + 11/28qls + 8/7ql (s-l)

M(s=0) = 0

M(s=2l) = -2ql²/2 + 11/282ql² + 8/7ql² = -ql²/14

Mmax ⇒ T=0 ⇒ s = 115/28l + l 

M(s= 43/28l) = [q(43/28l)2]/2 + 11/28ql (43/28l) + 8/7ql (15/28l)= 57/1568ql²

DIMENSIONAMENTO DI UN SOLAIO IN LEGNO

      In rosso è evidenziata la trave la quale si è scelta per effettuare il dimensionamento

sezione del solaio in legno

dobbiamo calcolarci l'altezza h della trave , mentre sono definiti i valori della base, del momento massimo e della resisenza di progetto fd 

La resistenza di progetto è fd= Kmod * fmk / γm

dove: 

Kmod (coefficiente che dipende dalla durata del carico e dall’umidità) = 0,6

fmK ( caratteristica resistenza a flessione) = 36 N/mmq

γm(coefficiente di sicurezza relativo al materiale) = 1,45

dove σmax= (Mmax/ Ix) * ymax = M/W

(W) è il modulo di resistenza a flessione che dipende dalle caratteristiche geometriche della sezione. In questo caso la trave ha sezione rettangolare, per cui (ymax = h/2), quindi avrò:

Ix = bh³/12

W= Ix/ymax

W= bh²/6 

quindi ymax/Ix = Wx è il modulo di resistenza a flessione della sezione   →   σmax= Mmax/(bh²/6)

da quest'ultima ci ricaviamo l'altezza  h = rad(6q/8b fd) * l

ANALISI DEI CARICHI

definiamo una base b= 30 cm 

 CARICHI STRUTTURALI qs

Trave = 1,00 m x 050 m x 0,30 m x 430 Kg/m³  = 0,65 KN/m²

Travicelli (abete)= 2 x 1,00 m x 0,10 m x 0,10 m x 600 Kg/m³ = 0,12 KN/m²

Tavolato  (abete) = 1,00 m x 1,00 m x 0,03 m x 600 Kg/m³ = 0,18 KN/m²

totale =      0,95 KN/m²

CARICHI PERMANENTI qp

Massetto = 1,00 x 1,00 m x 0,05 m x 1900 Kg/m³ = 0,95  KN/m²

Allettamento= 1,00 x 1,00 m x 0,03 m x 1800 Kg/m³ = 0,54  KN/m²

Pavimento = 1,00 m x 1,00 m x 0,01 m x 400 Kg/m³ = 0,40  KN/m²

Incidenza tramezzi = 1,00  KN/m²

Incidenza impianti = 0,50 KN/m²   

totale = 2,99  KN/m²

CARICO ACCIDENTALE qa

Locali d’abitazione = 2  KN/m²

 Totale dei carichi  = 5,94  KN/m²

qtot[Kn/m] = (qs+ qp+ qa) * i = 5,94 * 5 = 29,7 KN/m²

Insiriamo ora nella tabella excell i valori ricavati e ci troviamo l'altezza della trave 

L'altezza risulta essere circa 45 cm.

DIMENSIONAMENTO DI UN SOLAIO IN CALCESTRUZZO 

SEZIONE DEL SOLAIO

carico permanente q = 38 KN/m²

M = ql²/8 ( trave appoggiata appoggiata)

Imponiamo che fd= σmax = α * Rck/γm

dove:

Rck = resistenza caratteristica calcestruzzo = 30 N/mm²

E' stato scelto un calcestruzzo ordinario di classe C 25/30

α = coeff. riduttivo per la resistenza a lunga durata = 0,85

γm = coeff. riduttivo parziale di sicurezza relativo al cls = 1,5

σfa = fy/γs

dove:

fy = tensione di snervamento delle barre di acciaio = 450 N/mm²

γs = coeff. di sicurezza relativo all’acciao = 1,15

L'altezza di una sezione rettangolare è data da H = hu + δ

hu= r * rad(Mmax/b)

δ è distanza dal centro dei tondini al lembo inferiore della trave (5 cm)

ANALISI DEI CARICI

Carichi strutturali qs

Soletta = 1,00m x 1,00m x 0,04m x 2500Kg/m²   =  1KN/m²

Nervature = 2 x 0,1m x 0,2m x 1,00m x 2500 Kg/m²   = 1 KN/m²

Forati = 2 x 0,4 mx 0,2m x 1,00m x 800Kg/m²= 128    = 1,28 KN/m²

Totale = 3,28 KN/m²

Carichi permanenti qp

Intonaco = 1,00m x 1,00m x 30m = 0,30   KN/m²

Massetto = 1,00 mx 1,00m x 0,03m x 1900Kg/m²   =0, 57 KN/m²

Pavimento =   1,00mx 1,00m x 40m  =  0,40 KN/m²   

Incidenza tramezzi = 1  KN/m²  

Incidenza impianti = 0,50 KN/m²  

totale = 2,77

CARICO ACCIDENTALE qa

Locali d’abitazione = 2  KN/m²

Totale dei carichi  = 8,05  KN/m²

Inseriamo i valori nella tabella excel

L'altezza risulta essere circa 55 cm.

 Il metodo della linea elastica serve per risolvere l'equilibrio di strutture sia iperstatiche che isostatiche; consentendoci di determinare le reazioni vincolari, i diagrammi delle sollecitazioni , gli spostamenti e le deformazioni.              

Richiamiamo di seguito tutte le equazioni del modello di trave di bernoulli, distinguendole in tre gruppi in base al loro diverso significato fisico.

• EQUAZIONI DI BILANCIO esprimono il legame tra carichi esterni e sollecitazioni 

dN/ds + q1 = 0

dT/ds + q2 = 0

dM/ds + T = 0

• EQUAZIONI DI CONGRUENZA esprinono il legame tra deformazioni e spostamenti

E =    du/ds

y = dv/ds - φ = 0

X = dφ/ds

dove E = deformazione assiale

       y = scorrimento angolare

       X = curvatura

• LEGAME COSTITUTIVO ELASTICO esprimono il legame tra la deformazione e la sollecitazione

N = EA * E 

M = EI * X

Analizziamo il problema flessionale e prendiamo in considerazione le seguenti grandezze

v ; Y ; T ; M ; x

quindi non prendendo in considerazione le equazioni che riguardano lo sforzo normale, le equazioni che definiscono il problema flessionale sono :

dT/ds + q₂ = 0

dM/ds  + T = 0

M = EI * X

X = dφ/ds

φ= dv/ds

Prendiamo in considerazione l'equazione ( dM / ds ) + T = 0 e ci ricaviamo T = - dM / ds e sostituiamo la T in

( dT/ds ) + q₂ = 0

avremo che d/ds ( -dM/ds) + q₂ = 0 ⇒ -d²M/ds² + q₂ = 0 

X = dφ/ds - d/ds(dv/ds) = d²v/ds^{2 =} d²v/ds²

andiamo ora a sostituire φ= dv/ds in X= dφ/ds

avremo che X = dφ/ds - d/ds(dv/ds) = d²v/ds^{2 =} d²v/ds²

ci rimane solo l'equazione M = EIx

Sostituiamo la x e avremo che M = EI (d²v)/ds

sostituiamo poi l'equazione ricavata nell'equazione  -d²M/ds² + q₂ = 0 

si avrà che :

 d²/ds² ( EI * d²v/ds²) = q₂

portiamo EI al di fuori della derivata e avremo che 

EI d⁴v/ds⁴ = q₂  EQUAZIONE DIFFERENZIALE DELLA LINEA ELASTICA

L'equazione della linea elastica mette in relazione i carichi agenti sulla trave con gli spostamenti da essi prodotti , integrando quattro volte otteniamo la funzione spostamento

d⁴v/ds = q₂/EI

d³v/ds = q₂/EIs + c₁

d²v/ds = q²/EI * s²/2 + c₁s + c₂   (3)

dv/ds = q₂/EI + s³/6 + c₁ * s²/2 + c₂s + c₃   (2)

v(s) = q₂/EI * s⁴/24 + c₁*s³/6 + c₂ s_2/2 + c₃s + c_{4    spostamento}  (1)

Abbiamo così ottenuto quattro equazioni che dipendono dai vincoli quindi andiamo a sostituire le equazioni al bordo

Nell'incastro v(0) = 0 

Andando a sostituire nella 1 la condizione al bordo v(0) = 0 si ottiene v(s=0) = 0 --> C4 = 0

 φ(0) = 0

Sostituendo nella 2 si ottiene 

φ (s=0) --> c3=0

Nell'appoggio

v(l) = 0

sostituiamo nella 1 avremo che :

v(s=l)= 0 ⇒ - q₂l⁴/24EI + c₁l³/6 + c₂l²/2 = 0  (4)

Nel carrello il momento vale zero M (l) = 0

sostituendo nella 3 avremo che :

M(s=l) = 0 ⇒ -q₂l²/2EI + c₁l + c₂ = 0 

ci ricaviamo c_{2 =} q₂l²/2EI - c₁l    (5)

sostituiamo c₂ nella 4 

- q₂l⁴/24EI + c₁l³/6 + (q₂l²/2EI - c₁l ) * l²/2 = 0

- q₂l⁴/24EI + c₁l³/6 q₂l⁴/4EI - c₁l³/2 = 0

5q₂l⁴/24EI -1/3 l³ c₁ = 0

c₁ = 5/8 q₂l/EI

Andiamo a sostituire c₁ nella (5) e ricaviamo c₂

c₂ = -q₂l²/8EI

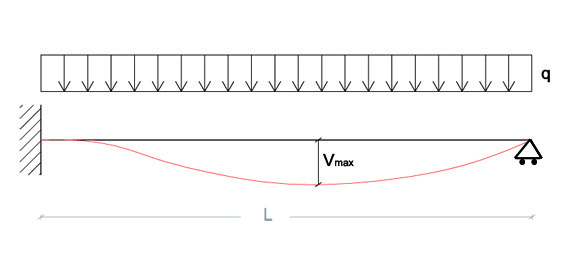
Abbiamo così trovato le quattro costanti di integrazione , ora dobbiamo calcolare l'abbassamento massimo . Sappiamo che y= dv/ds, ossia che la rotazione è la derivata dello spostamento . Quindi nel punto in cui la rotazione è nulla lo spostamento sarà massimo

φ = dv/ds = q₂/EI + s³/6 + c₁ * s²/2 + c₂s + c₃

Andiamo a sostituire nell'equazione scritta le costanti trovate 

φ (s) = - q₂/EI + s³/6 + 5/8 q₂l/EI s²/2 - q₂l²/8EI + 0 

poniamola uguale a zero 

φ (s) = - q₂/EI + s³/6 + 5/8 q₂l/EI s²/2 - q₂l²/8EI = 0

che possiamo scrivere come

q/2EI s * ( - s₂/3 + 5/8 ls - l²/4) = 0 

Questa equazione ha tre soluzioni. Una è data da s=0 ed altre due le troveremo svolgendo l'equazione di secondo grado 

1.  - s₂/3 + 5/8 ls - l²/4 = 0 
2.    s₂/3 + 5/8 ls - l²/4) = 0 

Poniamo 1/3 = A   -5/8 l = B  ⇒ As² - Bs - l₂/4 = 0 

Risolvendo con la formula del delta otteniamo due valori :

1.  1,3 l  ( soluzione non accettabile perchè s < l )
2. 0,57 l 

I punti di massimo della funzione spostamento si trovano uno a zero e l'altro a 0,57 l. Per ricavarci l'abbassamento massimo basta sostituire la s nell'equazione 4.

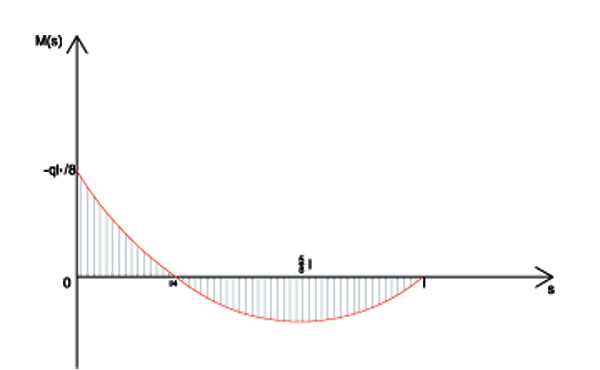
Adesso calcoliamo il momento M

Ms = -q/2 s₂ + 5/8 qls - ql²/8

Ora dobbiamo calcolare il punto in cui si annulla la derivata del momento M'(s)

M ( s=0) = -ql²/8

M ( s=l) = -ql²/2 + 5/8 ql² - ql²/8 = 0 

DIAGRAMMA DEL MOMENTO

Adesso calcoliamo il taglio 

T(s) = -dM/ds = - M'(s)

- M'(s) = T(s) = qs - 5/8 ql

T ( s=l) = ql - 5/8ql = 3/8 ql

DIAGRAMMA DEL TAGLIO

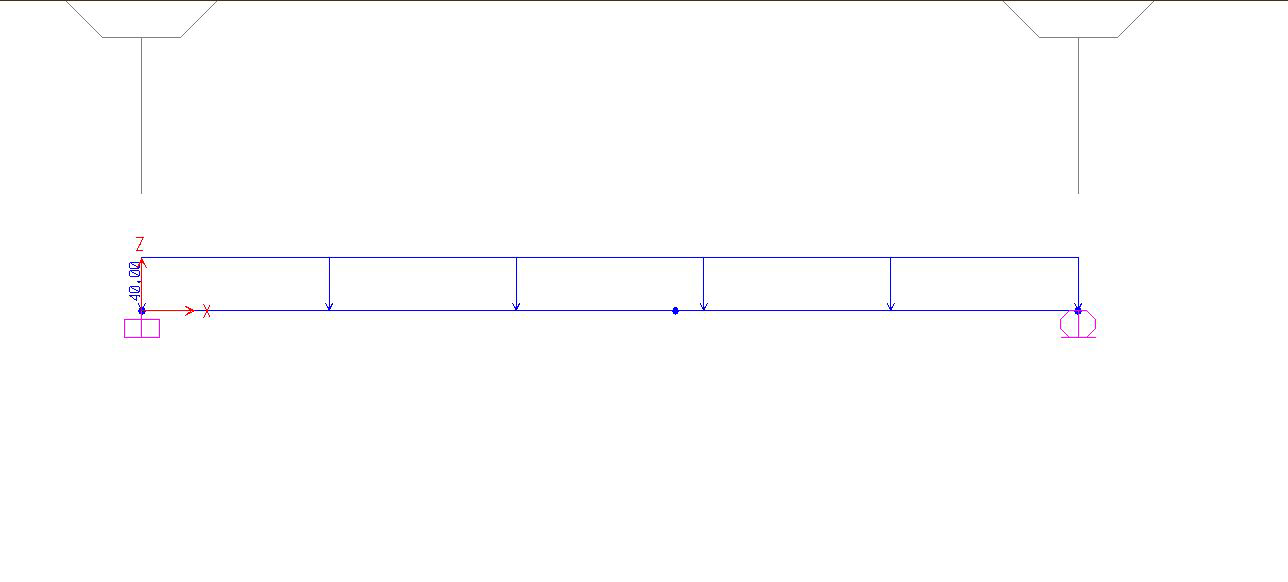
RISOLUZIONE SAP

Ho riprodotto la struttura in SAP disegnandola di lunghezza l = 2 e con un carico distribuito pari a q = 40 kN

1.    Divido ( con il comando Point ) la struttura in due parti, posizionando il punto ad una distanza di 0,57 dal punto zero e con asse y = z = 0 dato che dal calcolo a mano abbiamo visto che l'ammassamento massimo avviene in questo punto

L'analisi è stata fatta su due sezioni differenti , una rettangolare in acciaio cavo 

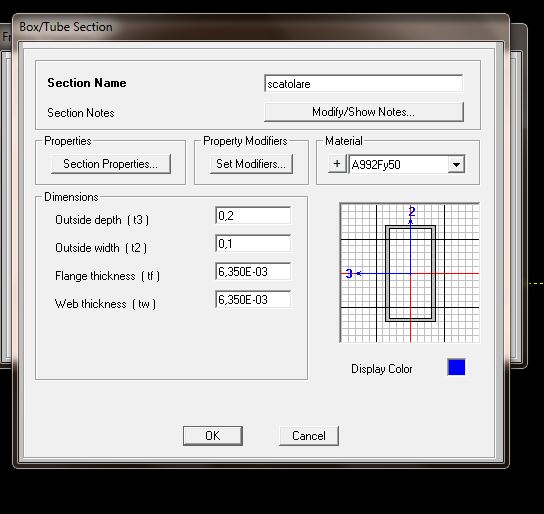
e l'altra in cemento armato 

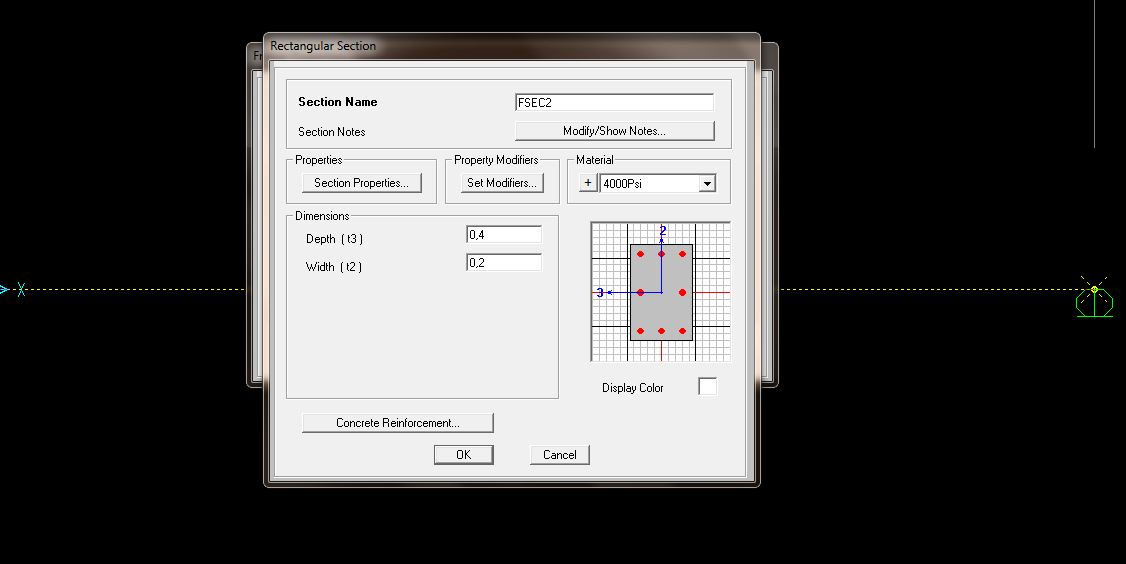
DEFORMATA

REAZIONI VINCOLARI

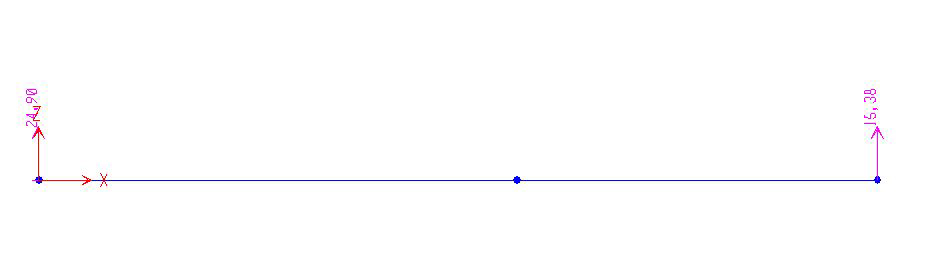
DIAGRAMMA DEL TAGLIO

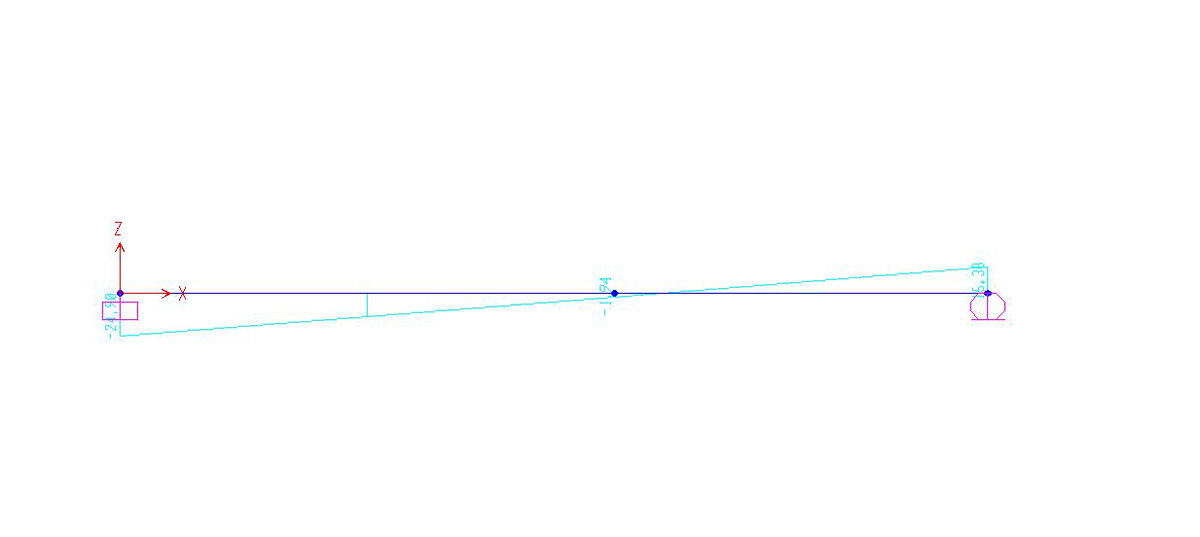
DIAGRAMMA DEL MOMENTO

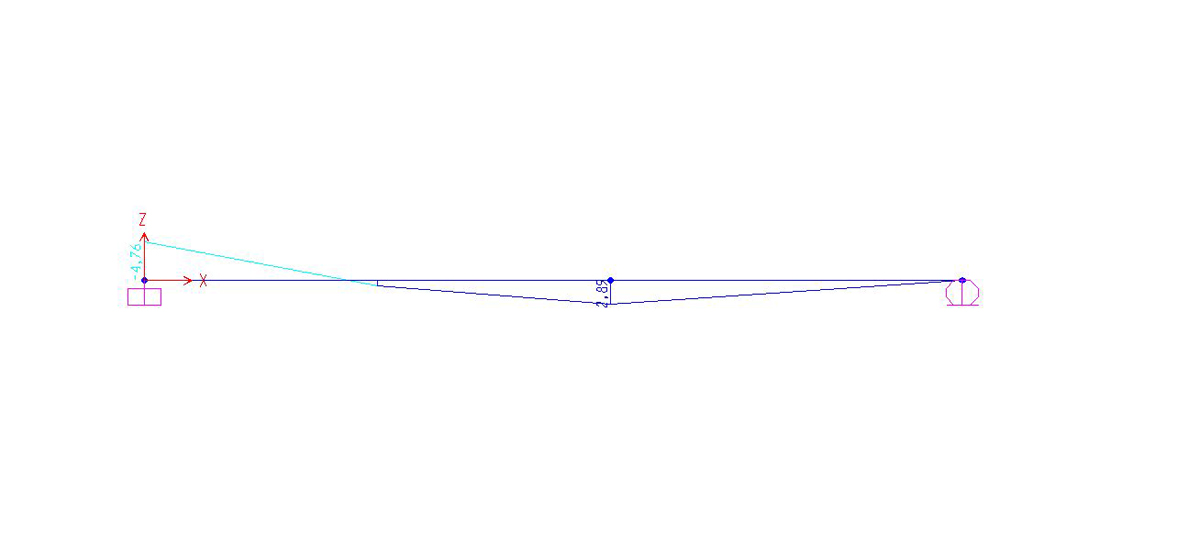
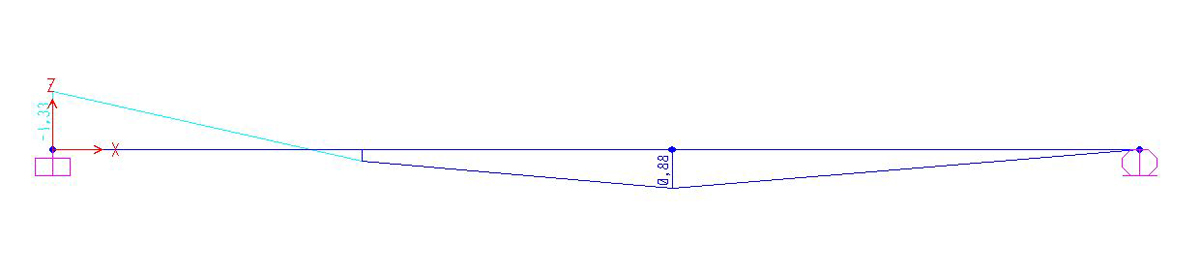
SEZIONE IN CEMENTO

REAZIONI VINCOLARI

DIAGRAMMA DEL TAGLIO

DIAGRAMMA DEL MOMENTO

RETICOLARE PIANA - METODO DI RITTER - 

SCHEMA DI CALCOLO

Per prima cosa verifico che la struttura sia isostatica; il numero dei gradi di libertà della struttura deve essere pari al numero di vincoli applicati su questa.

Ve + a = 2n

dove

Ve= vincoli esterni

a= numero aste

n= numero nodi

3 + 33 = 2 * 18 

36 = 36 

da questa uguaglianza si deduce che la struttura è isostatica.

Trovo ora le reazioni vincolari che risultano essere entrambe 9/2F poichè la struttura è simmetrica e simmetricamente caricata. Le reazioni vincolari sono dunque simmetriche.

Effettuo ora la sezione di ritter che divide la struttura in due, tagliando tre aste che convergono nello stesso nodo.

SEZIONE 1

Una volta effettuato il taglio virtuale si mettono in evidenza gli sforzi normali agenti sulle sezioni delle aste

N.B. Disegnare le forze N uscenti dalla sezione significa che sto considerando che le aste sezionate siano sottoposte a trazione (tiranti). 

Scrivo le tre equazioni di equilibrio a rotazione cambiando ogni volta il polo, che scelgo nel punto di incontro di due delle tre aste tagliate

• Trovo N₂₄ facendo polo nel punto 3

- N₂₄*L +FL - 9/2FL = 0

 N₂₄ = - 7/2F  

N₂₄ è negativo quindi l'asta 24 è un puntone    

• Trovo N₁₃ facendo polo nel punto 2

N₁₃*L= 0

L'asta 13 risulta essere scarica

• Trovo N₂₃ facendo l'equilibrio alla traslazione orizzontale 

√2/2 N₂₃ -7/2F = 0               

N₂₃ = 7V2 /2F      

N₂₃ è positivo , l'asta 23 è un tirante                    

SEZIONE 2

• Equazione alla traslazione verticale

N₁₂ + 9/2F = 0

N₁₂ = -9/2F 

L'asta 12 risulta essere compressa     

SEZIONE 3

• Trovo N₃₅ facendo polo in 4

N₃₅*L + FL - 9/2FL = 0

N₃₅ = 7/2F 

L'asta 35 è tesa      

• Trovo N₃₄ facendo la traslazione verticale 

N34 - F + 9/2F = 0

N34 = -7/2F  

L'asta 34 è compressa 

SEZIONE 4

• Trovo N46 facendo polo in 5

N₄₆*L + 3FL - 9/2F * 2L = 0

-N₄₆= - 6F

L'asta 46 è compressa 

• Trovo N₄₅ facendo l'equilibrio alla traslazione orizzontale 

√2/2 N₄₅ - 6F + 7/2F = 0

N₄₅ = (5V2)/2 F 

L'asta 45 è tesa

SEZIONE 5 

• Trovo N₅₇ facendo polo in 6 

N₅₇*L + 3FL - 9/2F * 2L = 0

N₅₇ = 6F

L'asta 57 è tesa  

• Trovo N₅₆ facendo l'equilibrio alla traslazione verticale

9/2F - 2F + N₅₆ = 0

N₅₆ = -5/2 F

SEZIONE 6

• Trovo N₆₈ facendo polo in 7 

-N₆₈*L - 9/2F*3L + 6FL= 0

N₆₈ = -15/2F

L'asta 68 è compressa

• Trovo N₆₈ facendo l'equilibrio alla traslazione orizzontale 

N₆₇ √2/2 - 15/2F + 6F = 0

N₆₇  = 3√2/2F

SEZIONE 7

• Trovo N₇₉ facendo polo in 8

9/2F - 3F + N₇₈ = 0

N₇₈ = -3/2F

L'asta 78 è compressa 

SEZIONE 8

• Trovo N₈₁₀ facendo polo in 9

-N810*L - 9/2F*4L + 10FL= 0

N₈₁₀ = -8F

L'asta 810 è compressa 

• Trovo N₈₉ facendo l'equilibrio alla traslazione orizzontale 

N₈₉ √2/2 + 15/2F + 8F = 0

N₈₉ = F√2/2

SEZIONE 9 

• Trovo N₉₁₀ facendo l'equilibrio alla traslazione verticale

- 4F + 9/2F + N₉₁₀ = 0

N910= - F/2

Lìasta 910 è compressa

Siccome la struttura è simmetrica e simmetricamente caricata , l'ho analizzato solamente per metà siccome le reazioni vincolari risultano essere simmetriche

RETICOLARE 3D - SAP - 

Disegnano la pianta, creando un nuovo layer , dato che SAP non legge in layer 0 di autocad, partendo da un modulo base L di 2 x 2 , facendo attenzione che ogni asta sia un elemento separato e la completiamo portando3d    

Selezioniamo tutto ed esplodiamo. Salviamo il file in formato dxf in modo da poterlo importare in SAP Apriamo SAP e importiamo il file autocad

FILE- IMPORT- AUTOCAD- dxf FILE

Si aprirà una tendina impostiamo come unità di misura KN, m, C e come “ Global Up Direction” impostiamo l’asse z ; diamo ok. Si aprirà un’altra tendina, nella voce “Frame” impostiamo il layer con il quale abbiamo disegnato, in questo caso layer 1

Una volta importata la struttura, bisogna eliminare gli errori , ossia fare in modo che le aste convergano bene nei nodi.

EDIT - EDIT POINTS - MERGE JOINTS - MERGE TOLERANCE (inserire un valore basso)

Inseriamo i vincoli

ASSIGN - JOINT - RESTRAINT 

  Quando si disegna in SAP, esso disegna sempre in automatico una sezione , quando importiamo il disegno invece non lo fa. Assegniamo una sezione, selezioniamo il disegno :

DEFINE - SECTION PROPERTIES - FRAME SECTION - ADD NEW POPERTY

selezioniamo il materiale; in questo caso abbiamo scelto una sezione circolare in acciaio

Assegnamo poi la forza concentrate  ( -40 , negative perchè la forza spinge verso il basso)

Rendiamo tutti i nodi delle cerniere interne e andiamo ad assegnargli il rilascio.

ASSIGN - FRAME - RELEASIS - MOMENT 3-3 - spuntiamo le caselle END e START

Il valore deve essere zero

Definiamo il peso proprio della struttura, dandogli valore zero

DEFINE - LOAD PATTERNS - SELF WEIGHT MULTIPLIER = 0

2.    Una volta fatto ciò , facciamo partire l’analisi senza tenere conto del MODAL

ANALYZE - RUN ANALYZE e leggiamo i risultati

DEFORMATA

REAZIONI VINCOLARI

DIAGRAMMA SFORZO NORMALE

Andando su DISPLAY - SHOW TABLES  ci appare una tabella degli abachi disponibili. Clicchiamo su ANALYSIS RESULTS . Ci compare una tabella in cui sono mostrati tutte le aste con i relativi sforzi normali

Possiamo inoltre esportare questa tabella in excel

FILE - EXPORT CURRENT TABLES - TO EXCEL