RISOLUZIONE DI UNA TRAVE CONTINUA - METODO DELLE FORZE

In questa esercitazione ci troviamo a risolvere una struttura iperstarica con il metodo delle forze. Il metodo delle forze consiste nel porre come incognite del problema alcune reazioni vincolari, il cui numero è pari al grado di iperstaticità della struttura presa in esame.

SCHEMA DI RIFERIMENTO

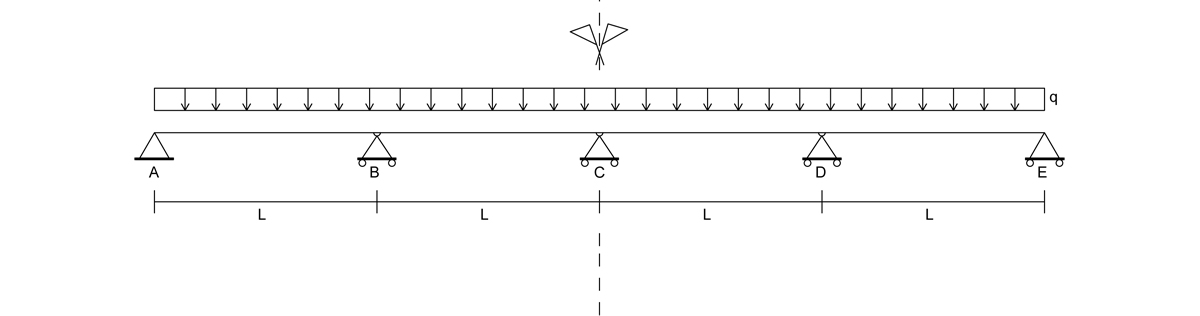
SCHEMA ISOSTATICO EQUIVALENTE - Trasformo le cerniere in C, B, D in cerniere interne, in modo da rompere la continuità della trave , abbassando i gradi di vincoli da tre a due. 

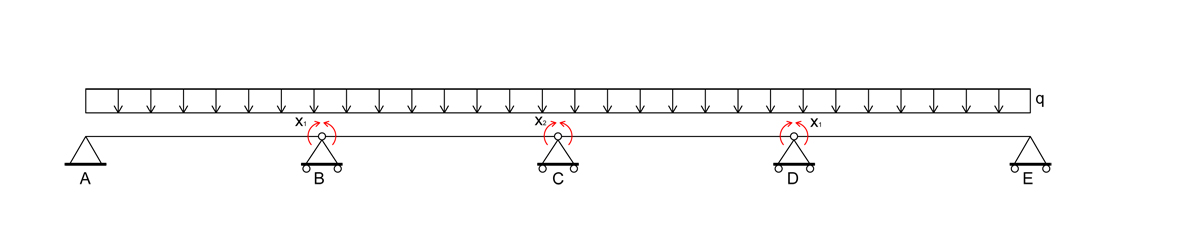
EQUAZIONI DI COMPATIBILITA' CINEMATICA

Impongo che ∆φ = 0 ossia che la rotazione in corrispondenza degli appoggi sia uguale a zero e mi ricavo i valori dovuti a x e al carico in base ai seguenti schemi notevoli :

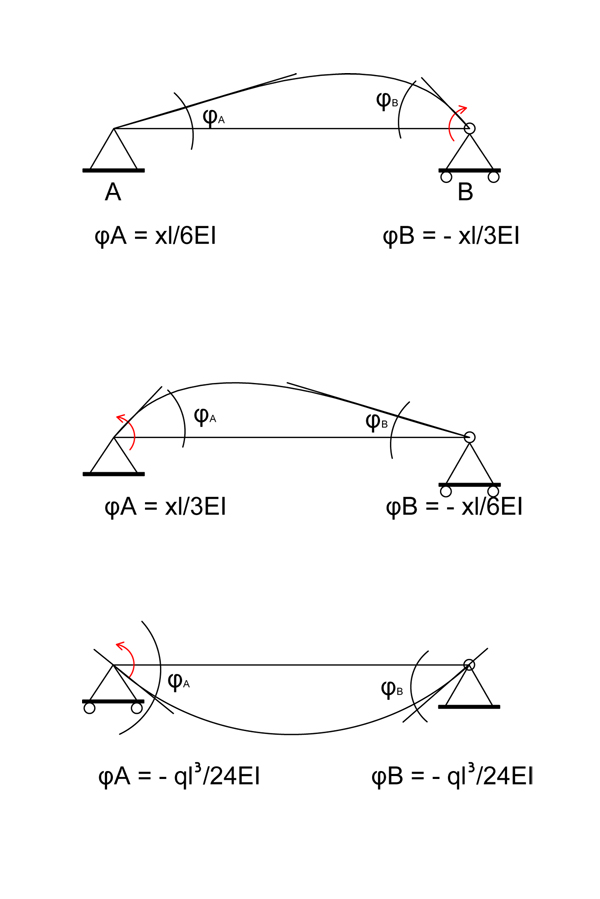
Punto B

∆φB = φBs – φBd = 0

φBs = φBs (q) + φBs (X₁) =  ql³/24EI – X₁L / 3EI

φBd = φBd (q) + φBd (X₁) + φBd (X₂) = - ql³/24EI + X₁L/3EI + X₂L/6EI

ql³/24EI – X1L / 3EI – (- ql³/24EI + X₁L/3EI + X₂L/6EI) = 0    

1. X₂= - 4 X₁+ ql²/2

Punto C

∆φC = φCs – φCd = 0

φCs = φCs (q) + φCs (X₁) + φCs (X₂) =  ql³/24EI – X₁L / 6EI – X₂L / 3EI

φCd = φCd (q) + φCd (X₁) + φCd (X₂) = - ql³/24EI + X₁L/6EI + X₂L/3EI

ql³/24EI – X₁L / 6EI – X₂L / 3EI – (- ql³/24EI + X₁L/6EI + X₂L/3EI) = 0  

1. X₁= - 2 X₂+ ql²/4

Metto a sistema le due equazioni ( 1 e 2 ) e mi ricavo le incognite X₁ e X₂ per sostituzione

X1= 3/28 ql²

 X2= 1/14 ql²

REAZIONI VINCOLARI 

- In relazione al carico

Per il principio di sovrapposizione degli effetti avremo :

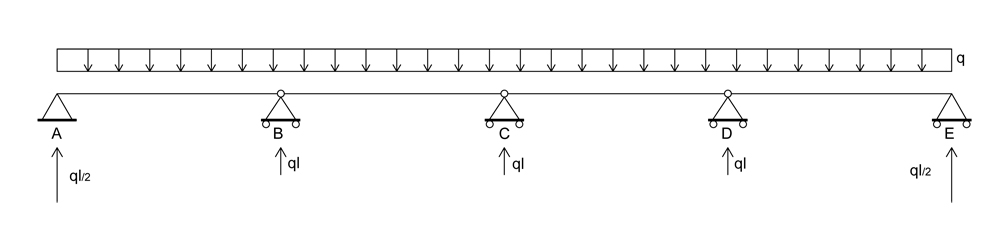
In relazione ai momenti X₁ e X₂ :

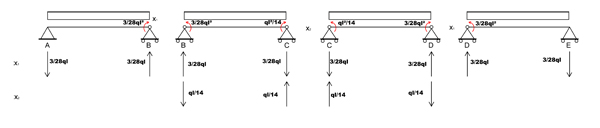
Ne ricavo che 

Per il principio di sovrapposizione degli effetti ( carico + momento) avremo :

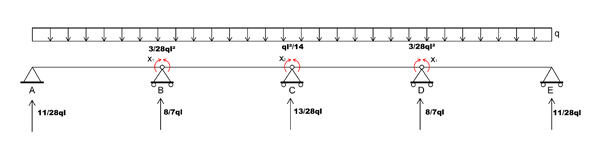
DIAGRAMMA DEL TAGLIO

asta 1 :

T(s) = -11/28 ql + qs 

T(s=0) = -11/28ql

T(s=l) = -11/28ql + ql = 17/28 ql

asta 2

T(s) = -11/28ql - 8/7ql + qs

T(s=0) = -11/28ql - 8/7ql + ql = -15/28 ql

T (s=2l) = -11/28 ql - 8/7ql + 2ql = 13/28ql

asta 3

T(s) = -11/28 ql - 8/7ql - 13/14ql + qs 

T(s=2l) = -11/28ql - 8/7ql + 2ql = -13/28 ql

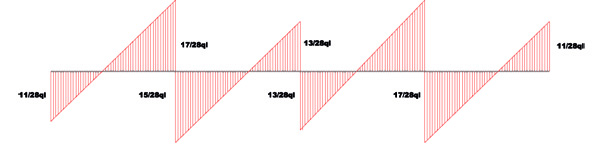
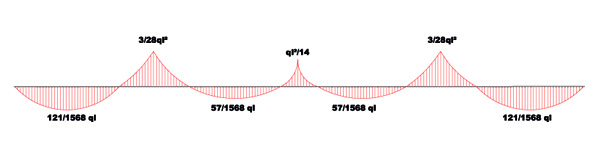
DIAGRAMMA DEL MOMENTO

asta 1 :

M(s) = qs²/2 + 11/28qls + 8/7ql (s-l)

M(s=0) = 0

M(s=2l) = -2ql²/2 + 11/28ql² + 8/7ql²= -ql

Mmax ⇒ T=0 ⇒ s = 11/28l

M(s= 11/28l) = -[q(11/28l)2]/2 + 11/28ql (11/28l) = 121 / 1568ql²

asta 2 

M(s) = -qs²/2 + 11/28qls + 8/7ql (s-l)

M(s=0) = 0

M(s=2l) = -2ql²/2 + 11/282ql² + 8/7ql² = -ql²/14

Mmax ⇒ T=0 ⇒ s = 115/28l + l 

M(s= 43/28l) = [q(43/28l)2]/2 + 11/28ql (43/28l) + 8/7ql (15/28l)= 57/1568ql²