DIMENSIONAMENTO DI MASSIMA DI UNA TRAVE INFLESSA

DIMENSIONAMENTO DI UN SOLAIO IN LEGNO

      In rosso è evidenziata la trave la quale si è scelta per effettuare il dimensionamento

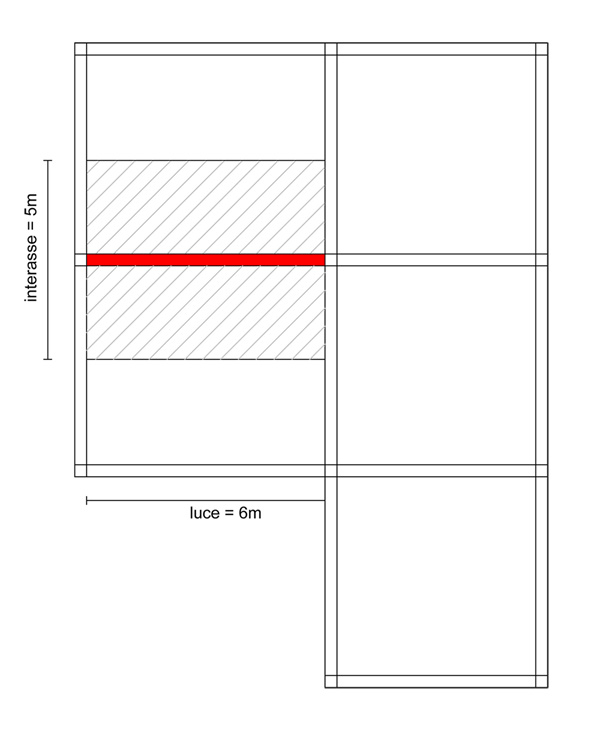
sezione del solaio in legno

dobbiamo calcolarci l'altezza h della trave , mentre sono definiti i valori della base, del momento massimo e della resisenza di progetto fd 

La resistenza di progetto è fd= Kmod * fmk / γm

dove: 

Kmod (coefficiente che dipende dalla durata del carico e dall’umidità) = 0,6

fmK ( caratteristica resistenza a flessione) = 36 N/mmq

γm(coefficiente di sicurezza relativo al materiale) = 1,45

dove σmax= (Mmax/ Ix) * ymax = M/W

(W) è il modulo di resistenza a flessione che dipende dalle caratteristiche geometriche della sezione. In questo caso la trave ha sezione rettangolare, per cui (ymax = h/2), quindi avrò:

Ix = bh³/12

W= Ix/ymax

W= bh²/6 

quindi ymax/Ix = Wx è il modulo di resistenza a flessione della sezione   →   σmax= Mmax/(bh²/6)

da quest'ultima ci ricaviamo l'altezza  h = rad(6q/8b fd) * l

ANALISI DEI CARICHI

definiamo una base b= 30 cm 

 CARICHI STRUTTURALI qs

Trave = 1,00 m x 050 m x 0,30 m x 430 Kg/m³  = 0,65 KN/m²

Travicelli (abete)= 2 x 1,00 m x 0,10 m x 0,10 m x 600 Kg/m³ = 0,12 KN/m²

Tavolato  (abete) = 1,00 m x 1,00 m x 0,03 m x 600 Kg/m³ = 0,18 KN/m²

totale =      0,95 KN/m²

CARICHI PERMANENTI qp

Massetto = 1,00 x 1,00 m x 0,05 m x 1900 Kg/m³ = 0,95  KN/m²

Allettamento= 1,00 x 1,00 m x 0,03 m x 1800 Kg/m³ = 0,54  KN/m²

Pavimento = 1,00 m x 1,00 m x 0,01 m x 400 Kg/m³ = 0,40  KN/m²

Incidenza tramezzi = 1,00  KN/m²

Incidenza impianti = 0,50 KN/m²   

totale = 2,99  KN/m²

CARICO ACCIDENTALE qa

Locali d’abitazione = 2  KN/m²

 Totale dei carichi  = 5,94  KN/m²

qtot[Kn/m] = (qs+ qp+ qa) * i = 5,94 * 5 = 29,7 KN/m²

Insiriamo ora nella tabella excell i valori ricavati e ci troviamo l'altezza della trave 

L'altezza risulta essere circa 45 cm.

DIMENSIONAMENTO DI UN SOLAIO IN CALCESTRUZZO 

SEZIONE DEL SOLAIO

carico permanente q = 38 KN/m²

M = ql²/8 ( trave appoggiata appoggiata)

Imponiamo che fd= σmax = α * Rck/γm

dove:

Rck = resistenza caratteristica calcestruzzo = 30 N/mm²

E' stato scelto un calcestruzzo ordinario di classe C 25/30

α = coeff. riduttivo per la resistenza a lunga durata = 0,85

γm = coeff. riduttivo parziale di sicurezza relativo al cls = 1,5

σfa = fy/γs

dove:

fy = tensione di snervamento delle barre di acciaio = 450 N/mm²

γs = coeff. di sicurezza relativo all’acciao = 1,15

L'altezza di una sezione rettangolare è data da H = hu + δ

hu= r * rad(Mmax/b)

δ è distanza dal centro dei tondini al lembo inferiore della trave (5 cm)

ANALISI DEI CARICI

Carichi strutturali qs

Soletta = 1,00m x 1,00m x 0,04m x 2500Kg/m²   =  1KN/m²

Nervature = 2 x 0,1m x 0,2m x 1,00m x 2500 Kg/m²   = 1 KN/m²

Forati = 2 x 0,4 mx 0,2m x 1,00m x 800Kg/m²= 128    = 1,28 KN/m²

Totale = 3,28 KN/m²

Carichi permanenti qp

Intonaco = 1,00m x 1,00m x 30m = 0,30   KN/m²

Massetto = 1,00 mx 1,00m x 0,03m x 1900Kg/m²   =0, 57 KN/m²

Pavimento =   1,00mx 1,00m x 40m  =  0,40 KN/m²   

Incidenza tramezzi = 1  KN/m²  

Incidenza impianti = 0,50 KN/m²  

totale = 2,77

CARICO ACCIDENTALE qa

Locali d’abitazione = 2  KN/m²

Totale dei carichi  = 8,05  KN/m²

Inseriamo i valori nella tabella excel

L'altezza risulta essere circa 55 cm.