Esercitazione sulla Rigidezza Torsionale

Per capire la rigidezza torsionale, abbiamo analizzato un nodo 3d costituito da tre aste incastrate e una mensola isostatica con carico distribuito. La struttura è 12 volte iperstatica in quanto essendo tridimensionale, un incastro ha 6 equazioni di vincolo e non 3. 

Come primo passaggio posso semplificare i calcoli sostituendo la mensola isostatica con l’effetto che produce ovvero un momento in corrispondenza del nodo. La forza ql verticale provocata dal carico, che diventa sforzo normale sul pilastro, teoricamente ci sarebbe, ma non viene in realtà considerata perché è un contenuto piccolissimo. Infatti, il pilastro è indeformabile assialmente, non si abbassa o accorcia in maniera visibile. Otteniamo quindi la seguente struttura equivalente:

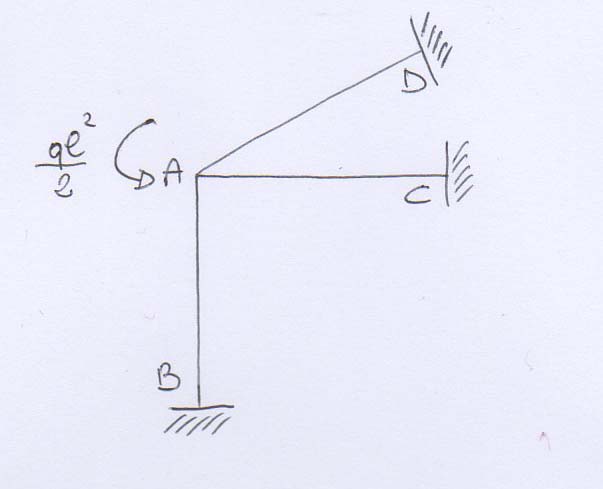
Il momento ql²/2 applicato nel nodo provoca una rotazione, così le aste AB e AC ruotano in maniera antioraria. 

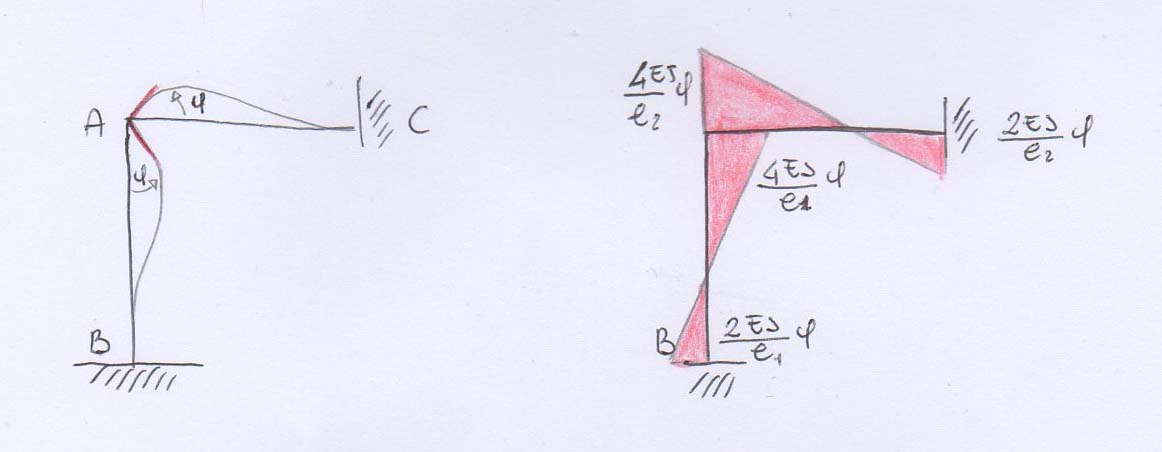
Il diagramma dei momenti mostra i valori ottenuti attraverso lo svolgimento della linea elastica sottostante.

Dal diagramma dei momenti, visto precedentemente, notiamo che il momento al nodo non si ribalta quindi suggerisce che il nodo non è in equilibrio. Infatti il momento ql²/2 oltre a provocare momento flettente nelle aste AB e AC che stanno sul piano xz ,  provoca un momento torcente nell’asta perpendicolare a queste AD che giace sul piano yz. Vengono così introdotti due concetti di rigidezza: flessionale e torsionale.

EQUILIBRIO AL NODO

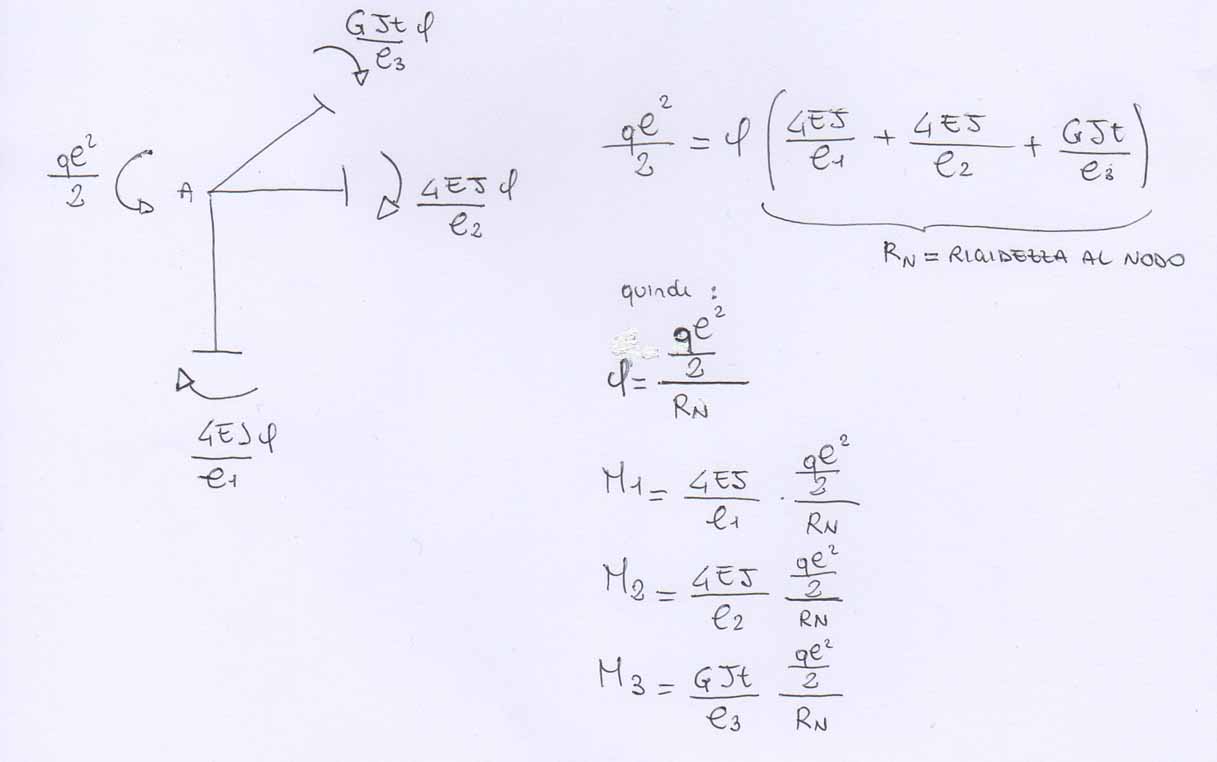
Ora analizzo come può variare la rigidezza torsionale a seconda del materiale e delle sezioni.

Lo studio sarà effettuato prima attraverso dei calcoli manualmente poi con sap per confronto.

Iniziamo con il CALCESTRUZZO

DATI

L = 6m

q= 5 KN

ql²/2= 90 KN m

Riproducendo anche su sap il nodo 3d con le 3 aste incastrate e un momento di 90 kN m applicato nel nodo, iniazialmente do a tutte e tre le aste una sezione di calcestruzzo rettangolare come per i calcoli manuali. nel definire la sezione è importante che anche su sap il cls abbia lo stesso modulo di elasticità e modulo di elasticità tangenziale.

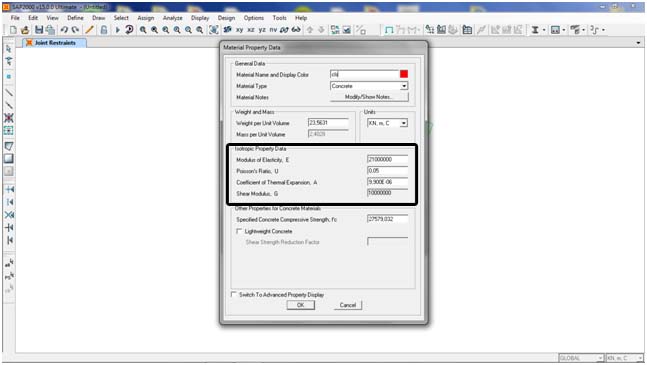
Analizzando questa struttura ottengo:

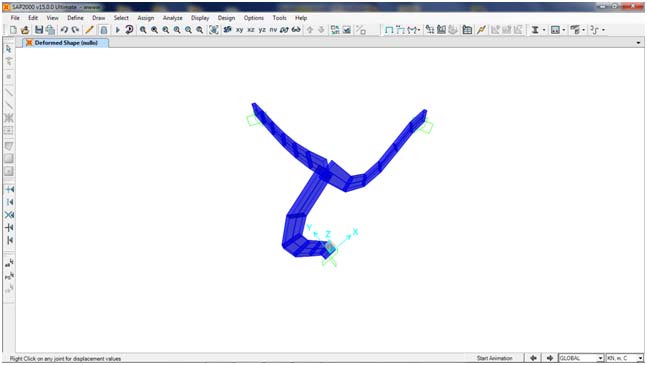
LA DEFORMATA E I VALORI DELLA ROTAZIONE

R₂=0,00094

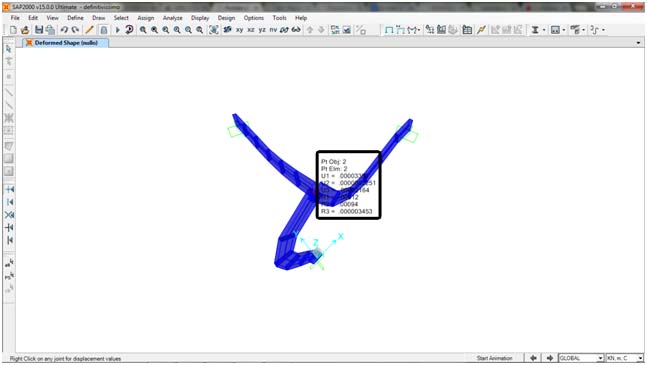
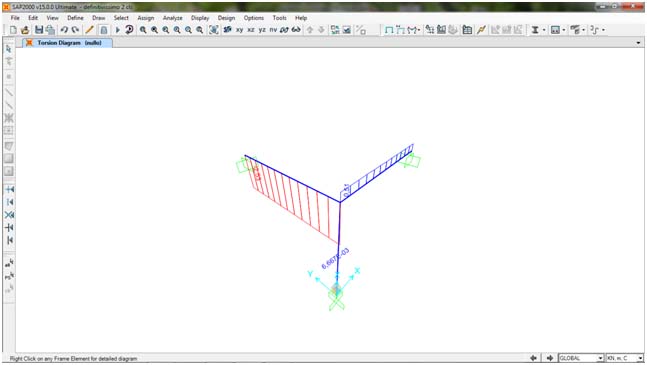
DIAGRAMMA MOMENTO TORCENTE

Nella seconda applicazione provo a cambiare la sezione della terza asta AD, assegnandogli una sezione circolare di diametro  0,36 m.

Lo riporto su sap e ottengo:

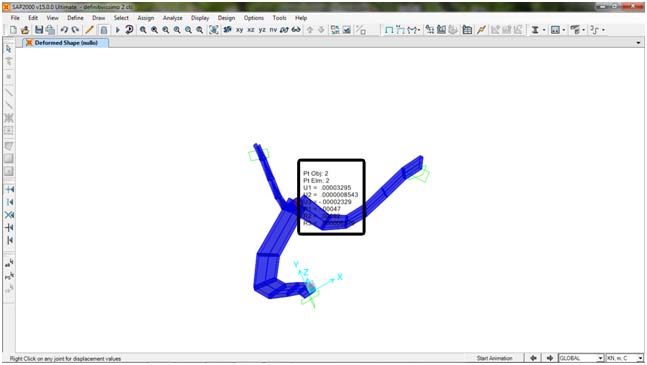
La DEFORMATA e i valori della rotazione: 

R₂=0,00092

Momento torcente

Vediamo ora l'ACCIAIO

Scegliendo per tutte e tre le aste una sezione HE di questo tipo:

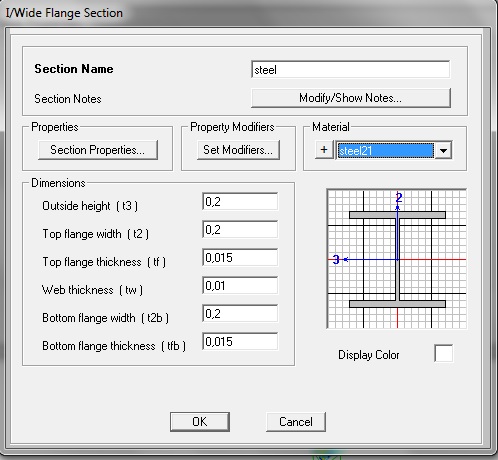
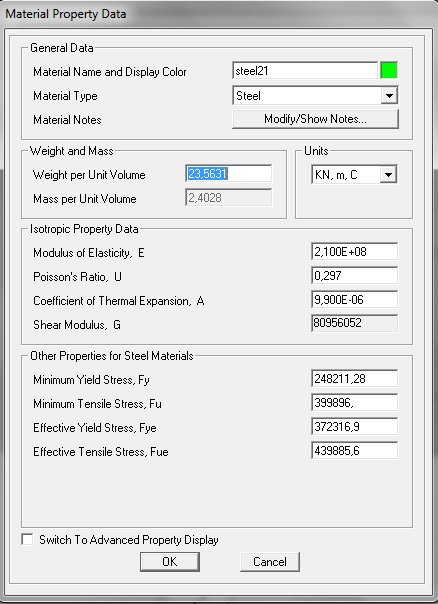
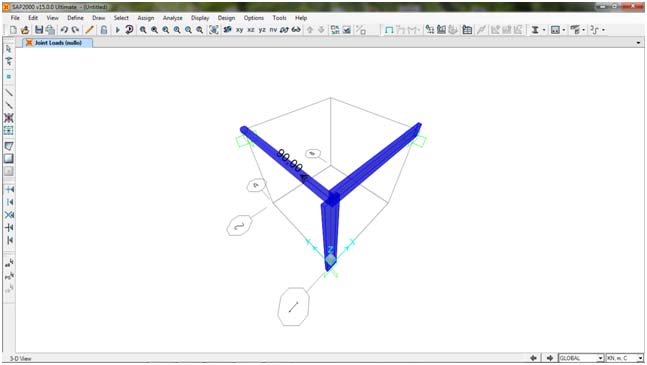
Applicando un momento lungo y pari a 90 KN m

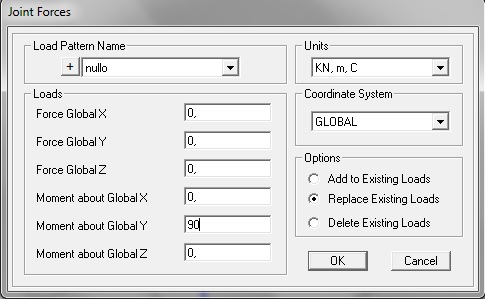
Ottengo i seguenti risultati:

DEFORMAZIONE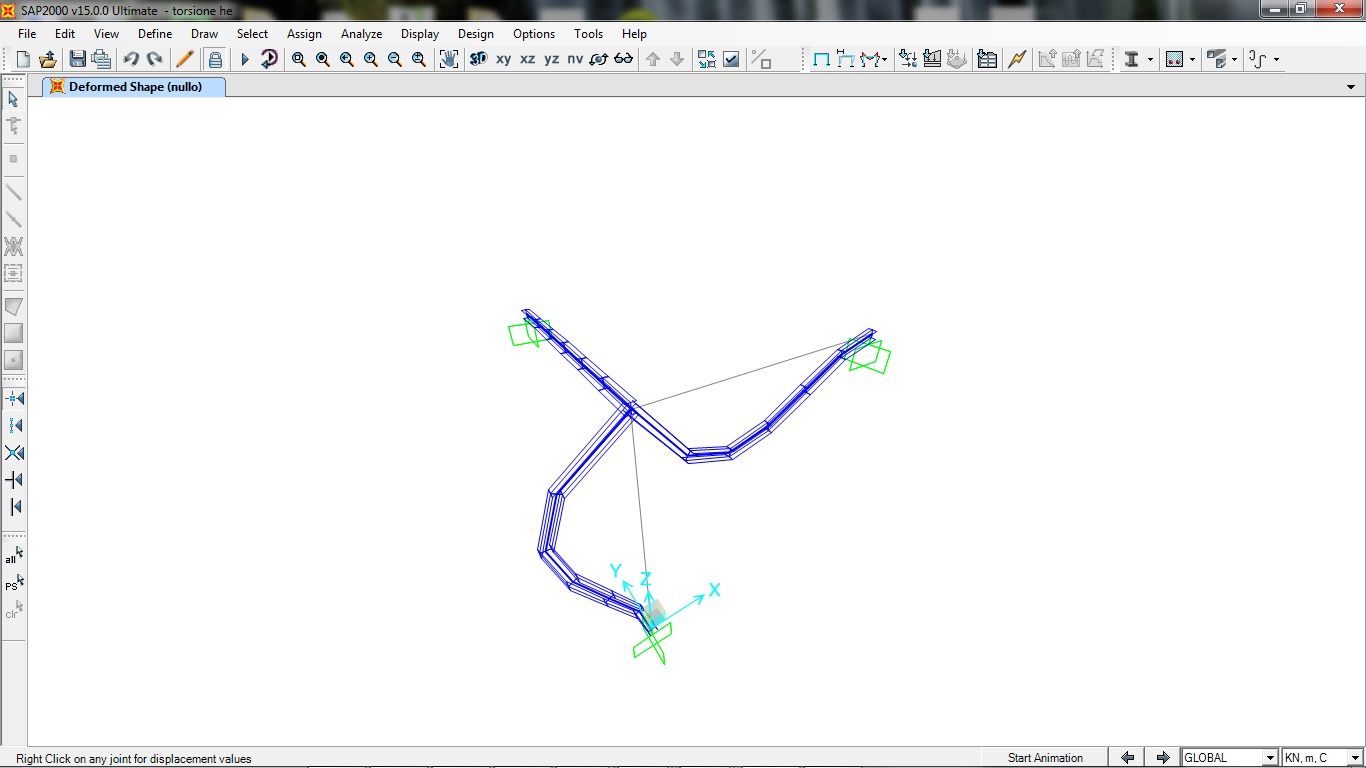

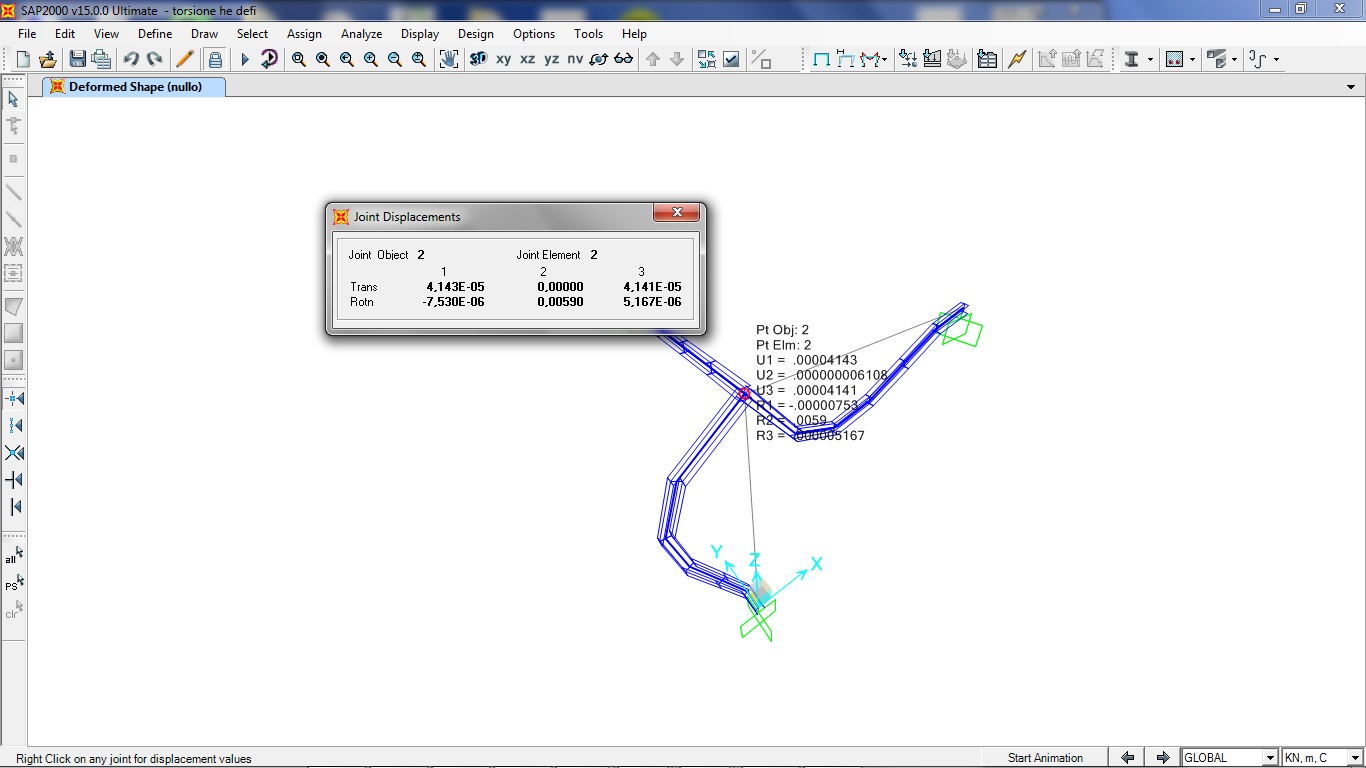
R2=0,0059

MOMENTO TORCENTE

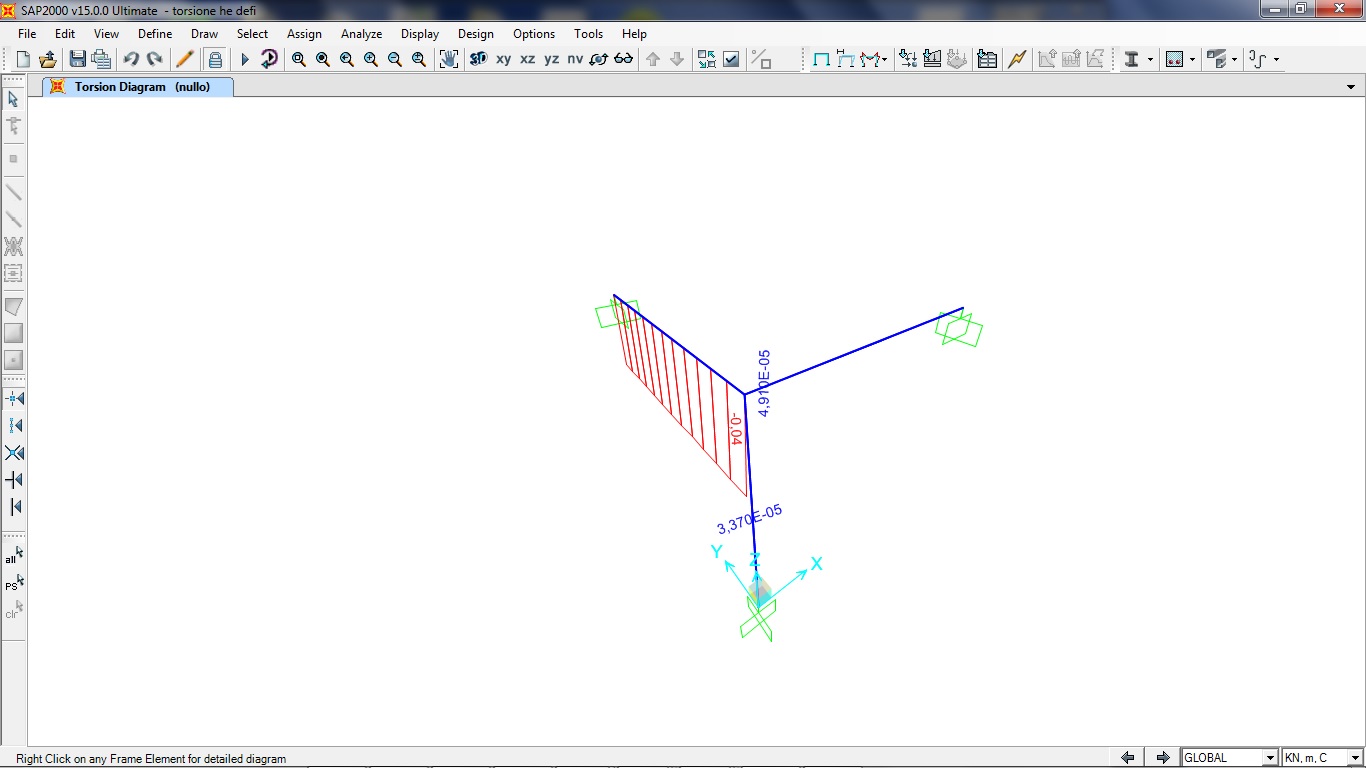
Ora cambio la sezione alla terza trave assegnandogli una sezione scatolare di questo tipo:

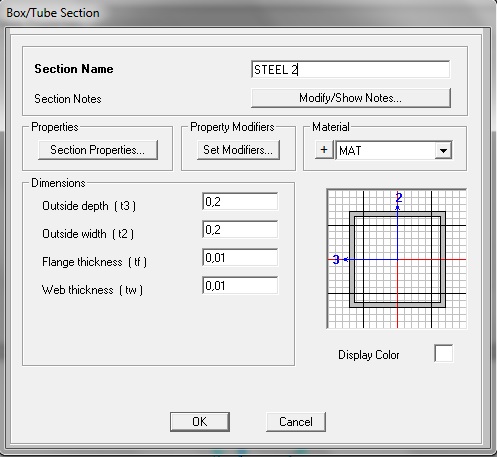
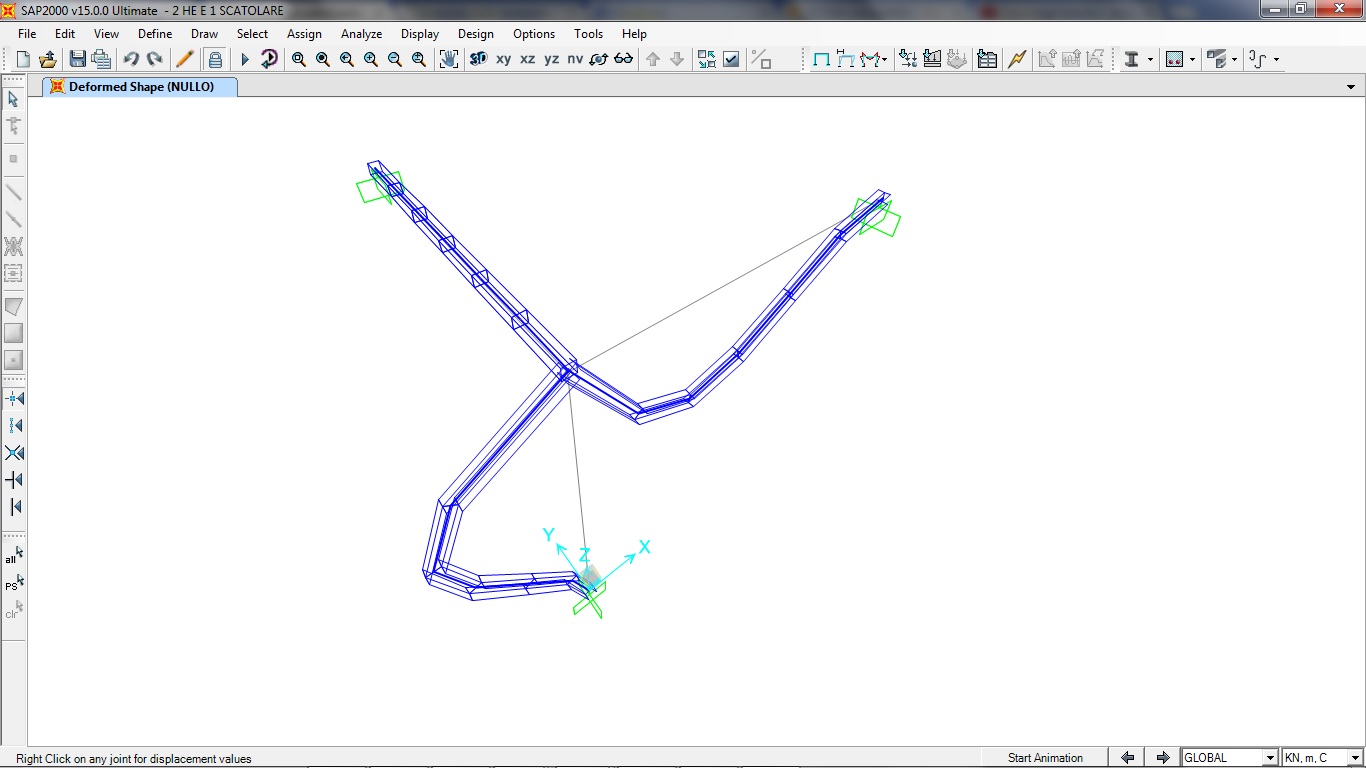
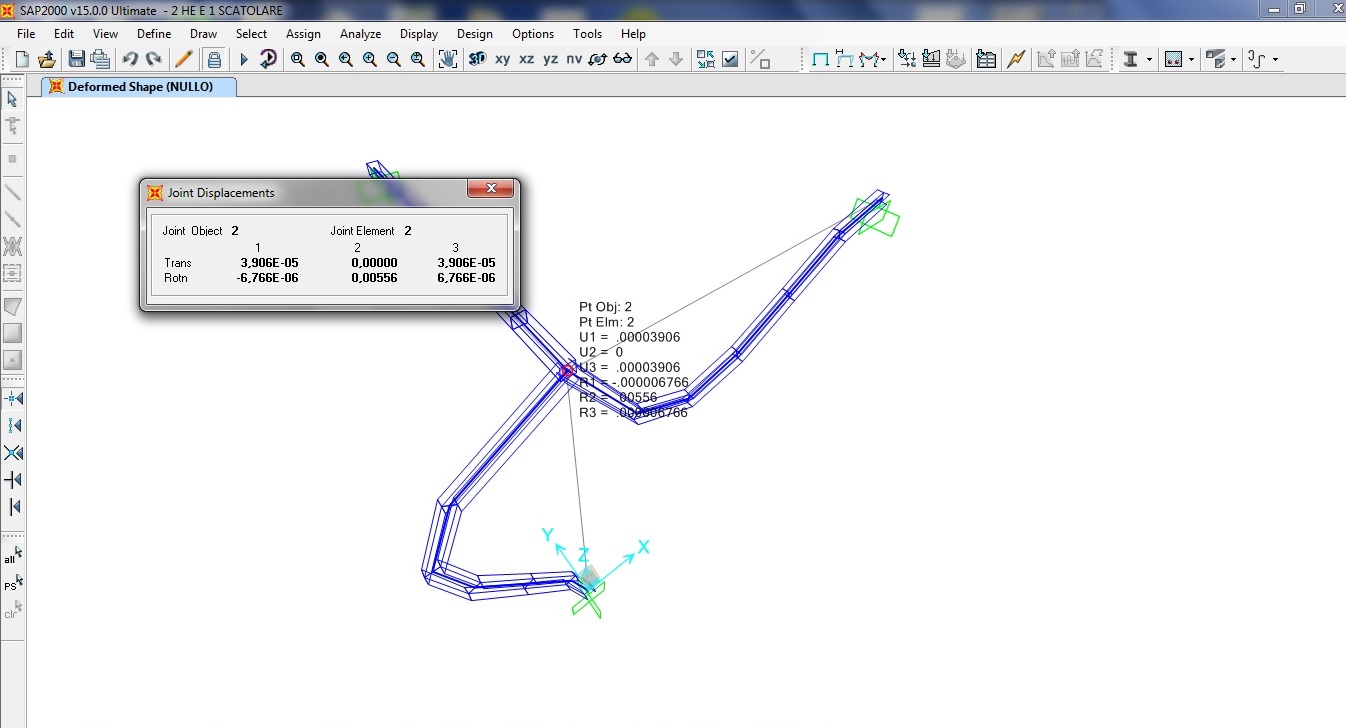
R2=0,00556

DIAGRAMMA MOMENTO TORCENTE

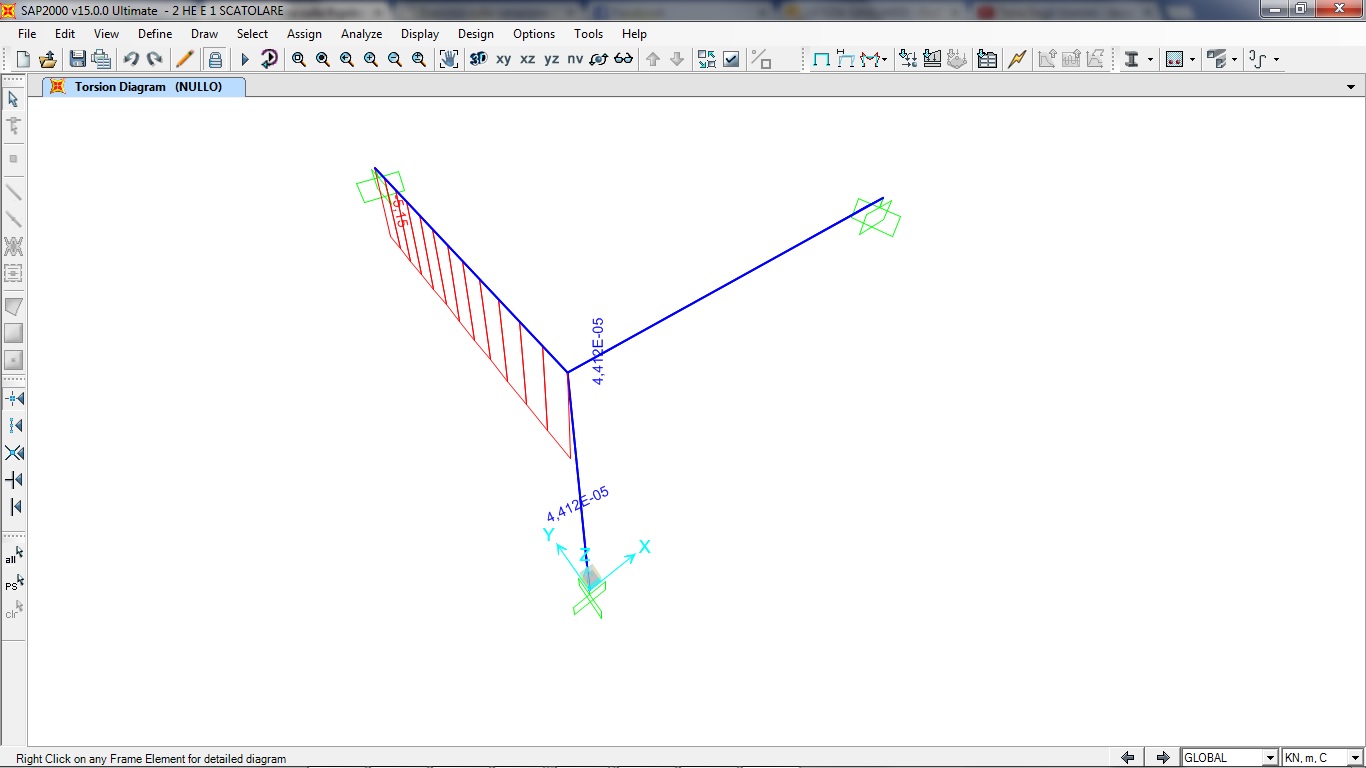
Dai risultati ottenuti possiamo notare che le sezioni in acciaio hanno una maggiore resistenza torsionale rispetto a quelle in cls, ma soprattutto le sezioni chiuse sono più rigide di quelle aperte, come possiamo notare nell'ultimo esempio dove il momento torcente è maggiore.