blog di letizia.gagliardi

GRATICCIO DI TRAVI

Il Graticcio di travi, utilizzato per grandi luci, è costituito da travi dirette lungo due direzioni perpendicolari. Si differenzia dalla gerarchia di travi perché non è costituito da travi principali e travi secondarie, ma tutte le travi collaborano allo stesso modo, hanno lo stesso momento di inerzia a prescindere dalla loro orditura e presentano un nodo che consente la trasmissione della rotazione .

RISOLUZIONE DI UN GRATICCIO

L’esercizio propone 2 travi entrambe doppiamente incastrate, su cui agisce una forza F all’incrocio tra le 2 aste. Il nodo in 3 d ha 6 gradi di libertà: esso può avere 3 differenti traslazioni, secondo i 3 assi x, y e z e 3 rotazioni intorno ai 3 assi. Analizziamo le deformate delle due aste separatamente e notiamo che:

SPOSTAMENTI

Per l’indeformabilità delle aste, che altrimenti si accorcerebbero o allungherebbero, non abbiamo spostamenti lungo x e lungo y,(u_x u_y =0), ma solamente lungo z ( u_z =delta)  a causa del carico F che agisce lungo z.

ROTAZIONI

φ_z non la consideriamo, φ_x è nulla poiché nell’asta BC la forza F  è applicata a l/2  dove la tangente è orizzontale,φ_y è l’unica ad esserci.

Le incognite sono quindi: lo spostamento (∂) e la rotazione (φ_y) che troveremo attraverso 2 equazioni di equilibrio al nodo:

Equilibrio CONTRO la traslazione verticale           

Equilibrio CONTRO la rotazione                              

Separiamo idealmente le due incognite, facendole agire separatamente e sovrapponendone poi gli effetti. Conoscendo i valori in una trave doppiamente incastrata possiamo quantificare Taglio e Momento flettente. 

Analizzando solo i gli effetti di ∂ vediamo:

Analizzando solo i gli effetti della rotazione oraria φ_yvediamo:

deformazioni, reazioni vincolari e momenti

La flessione della trave AC intorno all’asse y provoca la torsione di quella BD poiché ciò che è flessione in un piano diventa torsione nel piano ortogonale a questo.

EQUILIBRIO AL NODO CONTRO LA TRASLAZIONE VERTICALE

EQUILIBRIO AL NODO CONTRO LA ROTAZIONE INTORNO ALL’ASSE Y

Per trovare il valore dello spostamento e della rotazione, inseriamo i valori noti

Per una luce l=6 m e una forza F=20 KN e entrambe le aste hanno una sezione rettangolare in cls con a=0,67m e b=0,15m

Otteniamo i seguenti valori:

Verifico i risultati ottenuti con sap.

Disegno attraverso una griglia il graticcio in sap, gli assegno il materiale, la sezione scelta precedentemente, il modulo di elasticità e di elasticità tangenziale.

Notiamo che anche con sap ho trovato gli stessi valori per le rotazioni e gli spostamenti.

Otteniamo i seguenti valori:

u₃=u_z =0,0001 con segno negativo perché convenzionalmente l’asse positivo è verso l’alto

R₂= φ_Y = 0,00004

Per capire la rigidezza torsionale, abbiamo analizzato un nodo 3d costituito da tre aste incastrate e una mensola isostatica con carico distribuito. La struttura è 12 volte iperstatica in quanto essendo tridimensionale, un incastro ha 6 equazioni di vincolo e non 3. 

Come primo passaggio posso semplificare i calcoli sostituendo la mensola isostatica con l’effetto che produce ovvero un momento in corrispondenza del nodo. La forza ql verticale provocata dal carico, che diventa sforzo normale sul pilastro, teoricamente ci sarebbe, ma non viene in realtà considerata perché è un contenuto piccolissimo. Infatti, il pilastro è indeformabile assialmente, non si abbassa o accorcia in maniera visibile. Otteniamo quindi la seguente struttura equivalente:

Il momento ql²/2 applicato nel nodo provoca una rotazione, così le aste AB e AC ruotano in maniera antioraria. 

Il diagramma dei momenti mostra i valori ottenuti attraverso lo svolgimento della linea elastica sottostante.

Dal diagramma dei momenti, visto precedentemente, notiamo che il momento al nodo non si ribalta quindi suggerisce che il nodo non è in equilibrio. Infatti il momento ql²/2 oltre a provocare momento flettente nelle aste AB e AC che stanno sul piano xz ,  provoca un momento torcente nell’asta perpendicolare a queste AD che giace sul piano yz. Vengono così introdotti due concetti di rigidezza: flessionale e torsionale.

EQUILIBRIO AL NODO

Ora analizzo come può variare la rigidezza torsionale a seconda del materiale e delle sezioni.

Lo studio sarà effettuato prima attraverso dei calcoli manualmente poi con sap per confronto.

Iniziamo con il CALCESTRUZZO

DATI

L = 6m

q= 5 KN

ql²/2= 90 KN m

Riproducendo anche su sap il nodo 3d con le 3 aste incastrate e un momento di 90 kN m applicato nel nodo, iniazialmente do a tutte e tre le aste una sezione di calcestruzzo rettangolare come per i calcoli manuali. nel definire la sezione è importante che anche su sap il cls abbia lo stesso modulo di elasticità e modulo di elasticità tangenziale.

Analizzando questa struttura ottengo:

LA DEFORMATA E I VALORI DELLA ROTAZIONE

R₂=0,00094

DIAGRAMMA MOMENTO TORCENTE

Nella seconda applicazione provo a cambiare la sezione della terza asta AD, assegnandogli una sezione circolare di diametro  0,36 m.

Lo riporto su sap e ottengo:

La DEFORMATA e i valori della rotazione: 

R₂=0,00092

Momento torcente

Vediamo ora l'ACCIAIO

Scegliendo per tutte e tre le aste una sezione HE di questo tipo:

Applicando un momento lungo y pari a 90 KN m

Ottengo i seguenti risultati:

DEFORMAZIONE

R2=0,0059

MOMENTO TORCENTE

Ora cambio la sezione alla terza trave assegnandogli una sezione scatolare di questo tipo:

R2=0,00556

DIAGRAMMA MOMENTO TORCENTE

Dai risultati ottenuti possiamo notare che le sezioni in acciaio hanno una maggiore resistenza torsionale rispetto a quelle in cls, ma soprattutto le sezioni chiuse sono più rigide di quelle aperte, come possiamo notare nell'ultimo esempio dove il momento torcente è maggiore. 

Ipotizzo un impalcato in c.a. costituito da 12 pilastri rettangolari. Ogni telaio ha il compito di resistere  ai carichi verticali, ma anche a quelli orizzontali dovute alle forze sismiche. Sono stati quindi inseriti dei controventi rappresentati come molle in quanto assimilabili a vincoli cedevoli elasticamente con una determinata rigidezza che varia in funzione di alcuni parametri ad esempio la sezione dei pilastri. La rigidezza è la forza necessaria a produrre uno spostamento unitario.

1)   Calcolo delle rigidezze traslanti dei controventi dell'edificio

Per il cemento armato il modulo di Young(E)  è uguale a 21000 N/mm²

I pilastri 1-4 hanno dimensioni (base x altezza) 40x30 e quindi momento di INERZIA (B x H³/12) =90000 cm⁴

I pilastri 5-12 hanno dimensioni (base x altezza) 30x40 e quindi MOMENTO DI INERZIA (B x H³/12) =160000 cm⁴

In questo step si cerca di determinare qual è la forza, e quindi rigidezza, che i vari telai oppongo alla traslazione lungo il loro asse. La rigidezza del telaio è il risultato della somma della rigidezza di ogni pilastro ad esso appartenete :

Kᴛ= 12E Itotale/h³

2)   Tabella sinottica controventi e distanze

Nello step 2 vengono riportate le rigidezze traslanti dei telai e la rispettiva distanza dal punto O.

3)   Calcolo del centro di massa

L’impalcato viene semplificato in due aree rettangolari, di cui vengono trovati i baricentri. Il centro di massa si può cosi ottenere:

X_G (coordinata X del CENTRO di MASSA) =coordinata x del centro AREA1 * AREA 1 + coordinata x del centro di AREA 2 * AREA 2/AREA TOTALE DELL’IMPALCATO

Y_G(coordinata Y del CENTRO di MASSA) =coordinata y del centro AREA1 * AREA 1 + coordinata y del centro di AREA 2 * AREA 2/AREA TOTALE DELL’IMPALCATO

4)   Calcolo del centro di rigidezze e delle rigidezze globali

Il centro delle rigidezze è il centro del sistema di forze considerate. A differenza del centro delle masse che dipende dalla geometria della struttura, il centro delle rigidezze dipende dalla posizione dei controventi.

X_C (coordinata X del CENTRO DELLE RIGIDEZZE)= sommatoria delle rigidezza traslanti di ciascun controvento verticali * distanza verticale dei controventi dal punto 0 /rigidezza totale verticale.

Y_C(coordinata Y del CENTRO DELLE RIGIDEZZE)= sommatoria delle rigidezza traslanti di ciascun controvento orizzontale * distanza orizzontale dei controventi dal punto 0 /rigidezza totale orizzontale.

5)  Analisi dei carichi sismici

6)  Ripartizione della forza sismica

La TRAVE VIERENDEEL si comporta coma un telaio shear type ribaltato, per cui, presenta pilastri infinitamente rigidi e traversi flessibili. Ne deriva che la forza (F) fa traslare il ritto di una quantità δ, trascinando con sé i traversi che si deformano.

La presenza dei nodi incastro e l’ipotesi di rigidezza flessionale infinita dei pilastri, impone però ai nodi una rotazione nulla. Il traverso si trova nella situazione di una trave doppiamente incastrata  con un sistema che è tre volte iperstatico. Supponendo che uno dei due incastri ceda, avviene una deformazione e quindi una curvatura.

Per sapere quanto valgono taglio e momento risolvo la struttura iperstatica con il metodo della linea elastica.

Ottengo quindi i seguenti valori:

Dalle equazioni di equilibrio alla traslazione verticale dei pilastri posso risalire agli spostamenti, ai tagli e ai momenti.

DIAGRAMMA TAGLIO dei TRAVERSI

DIAGRAMMA MOMENTI dei TRAVERSI

Più semplicemente si potevano conoscere i valori del taglio e del momento facendo pochi calcoli. Per il taglio bastava sommare tutte le forze agenti sulla trave e successivamente dividerli per due. Per il momento,osservando la deformata si vede dove la curvatura è nulla e quindi anche il momento è nullo. Basta moltiplicare quindi la forza di taglio per il suo braccio l/2 per avere i valori dei momenti.

Per conoscere i valori del momento su ogni pilastro, calcolo l’equilibrio in ogni nodo.

Mpilastro=M1+M2(se sono entrembi orario producono un momento nei pilastri antiorario)

Per il taglio nei pilastri applico la seguente regola: 

e quindi ottengo per tutti i pilastri i seguenti valori:

DIAGRAMMA TAGLIO dei PILASTRI

DIAGRAMMA MOMENTO dei PILASTRI

VERIFICA CON SAP

Disegno la trave vierendeel a sbalzo di L =10 m attravarso la griglia, gli assegno i 2 vincoli di incastro, il peso nullo alla struttura e le forze applicate in z all'incrocio tra travi e pilastri pari a -10 KN m.

Successivamente per poter avere un comportamento simile a quello della trave vierendeel devo assegnare ai pilastri una rigidezza infinita. Su Sap ciò si può ottenere o dando ai pilastri una sezione con modulo di elasticità molto alto oppure assegnandogli una sezione molto grossa. Scelgo la seconda opzione.

Assegno ai traversi una sezione di questo tipo:

e ai RITTI una sezione di questo tipo:

Per ottenere delle sezioni di questo tipo

Faccio partire l'analisi con Run e ottengo:

DEFORMATA

DIAGRAMMA TAGLIO

DIAGRAMMA MOMENTO

TRAVE VIERENDEEL DOPPIAMENTE INCASTRATA

DEFORMATA

Essendo una struttura simmetrica ne analizzo solamente la metà.

EQUILIBRIO AI NODI

DIAGRAMMA MOMENTI

Analizzandola con SAP, ottengo i seguenti risultati:

L’esercitazione presenta una struttura tre volte iperstatica costituita da una trave continua su appoggi. La risoluzione è ottenuta attraverso il METODO DELLE FORZE.

 Si procede nel seguente modo:

1. Si sceglie la struttura isostatica di riferimento  più conveniente ponendo delle  incognite iperstatiche, il cui numero è pari al grado di iperstaticità della struttura. Nel nostro caso, da una trave continua si passa a staccare la struttura in più travi appoggiate-appoggiate. La reazione vincolare incognita che andiamo a scegliere coincide con il momento flettente ed il suo effetto cinematico è quello di evitare la rotazione relativa delle sezioni su cui agisce.

Inoltre ci troviamo di fronte ad una simmetria. Infatti dividendo la struttura a metà (Punto C) notiamo che nella parte destra e nella parte sinistra è presente lo stesso carico distribuito (q) e la stessa luce (l).  Per cui è possibile studiare solamente metà della struttura, perché successivamente avrò le stesse reazioni vincolari e azioni di contatto specchiandola.

Si ricercano quindi solo le incognite x1 (B) e x2 (C) . 

2. Si scrivono le equazioni di compatibilità cinematica che ripristinano i vincoli cinematici soppressi dalla trasformazione del vincolo cinematico in reazione vincolari. In questo caso impongo che le rotazioni a destra e a sinistra rispettivamente dei punti B e C siano uguali in quanto la rotazione relativa deve essere nulla.

3. Si risolve il sistema di equazioni per la determinazione delle incognite iperstatiche x1 e x2.

4. Indico le reazioni vincolari e si procede con l’applicazione del principio di sovrapposizione degli effetti per la determinazione delle azioni di contatto sulla struttura iperstatica.

5. I conseguenti diagrammi del taglio e del momento.

Nel metodo delle forze, le incognite sono le reazioni vincolari iperstatiche e le equazioni risolutive sono equazioni algebriche, che hanno il significato meccanico di equazioni di vincolo. La difficoltà sta nel riuscire a scegliere bene la struttura isostatica equivalente e nella capacità di applicazione sistematica del principio di sovrapposizione degli effetti.

DIMENSIONAMENTO TRAVE in CLS ARMATO

. 

1.Disegnare una pianta su autocad con pilastri, travi e ordire i solai lungo il lato più corto.

2.Considerare la trave più sollecitata.

INTERASSE (I) =4,85m

LUCE (L) = 6m

BASE TRAVE (b) = 30 cm

DELTA (d)=0,5 cm

SOLAIO IN LATERO-CEMENTO

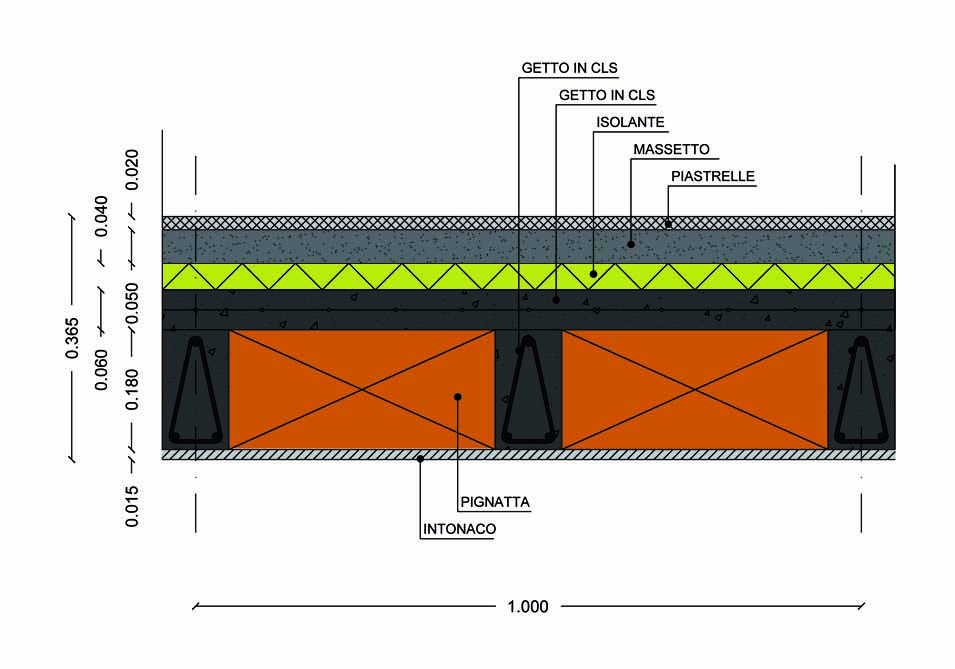
3.Calcolo qs ( Peso proprio dei materiali strutturali)

In un mq:

 PIGNATTE

Larghezza x altezza x profondità x peso specifico materiale (mattoni forati 8 KN/mc)

(0,40 x 0,18 x 1) x 8=0,576 KN/mq

Poiché in 1mq con le misure considerate sono presenti 2 pignatte

0,576 x 2 =1,152 KN/mq

SOLETTA

Larghezza x altezza x profondità x peso specifico materiale (Calcestruzzo armato e/o precompresso  25 KN/Mc)

(1 x 0,06 x 1 x 25) = 1,5 KN/mq

TRAVETTI

Larghezza x altezza x profondità x peso specifico materiale (Calcestruzzo armato e/o precompresso 25 KN/Mc )

(0,1 x 0,18 x 1 x 25) = 0,45 KN/mq

Poiché in 1mq con le misure considerate sono presenti 2 travetti

0,45 x 2 = 0,9 KN/mq

4.Calcolo qp (Carichi permanenti non strutturali)

INCIDENZA IMPIANTI 0,5 KN/mq

INCIDENZA ELEMENTI DIVISORI INTERNI(da normativa  compresa tra 0,40 a 2 KN/mq) 1,60 KN/mq

INTONACO SOFFITTO

Larghezza x altezza x profondità x peso specifico materiale (Malta di calce 18 KN/Mc )

1 x 0,015 x 1 x 18 = 0,27 KN/ mq

ISOLANTI

Larghezza x altezza x profondità x peso specifico materiale (Fibre di minerali o di vetro 0,5 KN/Mc )

1 x 0,04 x 1 x 0,5 = 0,02 KN/ mq

MASSETTO

Larghezza x altezza x profondità x peso specifico materiale(Calcestruzzo di sabbia e cemento18 KN/Mc )

1 x 0,05 x 1 x 18 = 0,9 KN/mq

PIASTRELLE

Larghezza x altezza x profondità x peso specifico materiale (Gres porcellanato con colla 23 KN/Mc )

1 x 0,02 x 1 x 23 = 0,46 KN/mq

Qp TOTALE:   0,5 + 1,60 + 0,27 + 0,02 + 0,9 + 0,46 = 3,75 KN/mq

5. Calcolo qa (sovraccarichi accidentali)

Per Ambienti ad uso residenziale la Normativa prevede:

qa= 2,00 KN/mq

6.Inserisco i Valori nella Tabella Excel dell’interasse, del qs, qp, qa.

Dalla somma dei 3 carichi (qs + qp + qa) moltiplicati per l’interasse ottengo il q totale.

Q=45,1147 KN/m

7.Inserendo la Luce (6m) ottengo il Momento massimo (q x L ^2 / 8) (se si considera una trave cerniera- carrello sottoposta a carico distribuito q)

M=203,0162 KN*m

Il calcestruzzo è un materiale composto, fatto di acqua,cemento e inerti di vario tipo (sabbia, ghiaia). Non è quindi un materiale omogeneo per cui è necessario tenerne conto, utilizzando un coefficiente di omogenizzazione nel calcolo. La sua resistenza a trazione è minore di quella a compressione. Quindi per sopperire alla bassa resistenza a trazione, nel cemento armato vengono disposte barre di acciaio dove le fibre sono tese, ovvero le inferiori. (Avremo quindi il cls compresso e l'acciao del cls teso). 

8. Inserisco fy (Limite di snervamento)  che per la classe di resistenza dell’acciaio da armatura B450C (più duttile quindi utilizzabile per zona sismica) deve essere 450MPa.

9. Di conseguenza ottengo sig_fa ( la resistenza di calcolo dell’acciaio che è riferita alla tensione di snervamento, importante momento di crisi del materiale, dopo il quele non è più elastico-lineare) = fy /( il coefficiente parziale di sicurezza relativo all’acciaio), pari a 1,15.

10. Scelgo un Rck (la resistenza caratteristica cilindrica a compressione del calcestruzzo a 28 giorni) uguale a 35 (compreso in una categoria di calcestruzzo ordinario)e ottengo quindisig_ca.

sig_ca ( resistenza di calcolo a compressione del calcestruzzo) = Rck (la resistenza caratteristica cilindrica a compressione del calcestruzzo a 28 giorni) x (il coeffciente riduttivo per le resistenze di lunga durata), pari a 0,85,/ (il coefficiente parziale di sicurezza relativo al calcestruzzo), pari ad 1,5.

11. Ottengo così l’altezza della trave e tutti gli altri valori di seguito.

H =42,96 cm

Il dimensionamento di una trave significa progettare a resistenza, ovvero assegnando una funzione, imporre che la struttura resista ai carichi implicati dalla funzione stessa, scegliendo il materiale e la geometria affinchè la reistenza sia garantita. La resistenza è il massimo valore che la tensione può sopportare prima di rompersi. Quantificare la resistenza è misurare la tensione massima del materiale. Nell'ambito di progetto di una struttura è necessario considerare le tensioni ammissibili, stumento utile in ambito di sicurezza. Il progetto alle tensioni ammissibili è il dimensionamento della struttura in modo che la sua tensione massima sia uguale alla tensione ammissibile relativa al materiale. Ciò ci permette di dimensionare l'altezza di una trave mantenendo un alto coefficiente di sicurezza. Infatti non si prende come valore massimo di riferimento il valore di snervamento,primo punto di crisi del materiale, ma una sua frazione dove v è il coefficiente di sicurezza diverso a seconda del grado di fiducia che una società ha nella produzione di una materiale.

Per il calcestruzzo:

LA TRAVE RETICOLARE 

Le strutture reticolari sono strutture che hanno il vantaggio di essere leggere e utilizzabili per grandi luci. Sono costituite da aste, che possono essere tese (tiranti) oppure compresse (puntoni) collegate tra loro tramite cerniere interne, i nodi. La struttura presenta un corrente superiore, uno inferiore, aste diagonali e montanti verticali. E' composta da una serie di trinagoli e risulta isostatica in quanto i gradi di libertà sono uguali ai gradi di vincolo. Per calcolare il grado di vincolo di ogni asta utilizzo la seguente formula:2(n – 1) dove n = numero di aste che confluiscono nel nodo.     

Solitamente nelle strutture reticolari il corrente superiore è teso, quello inferiore compresso e i montanti quasi sempre compressi. Dopo aver trovato le reazioni vincolari, due sono i metodi per analizzare una struttura reticolare:

 METODO DEI NODI  e METODO DELLE SEZIONI DI RITTER

Per quanto riguarda il METODO DEI NODI è fodamentale capire l'ordine con cui si decide di risolvere la struttura. Generalmente si sceglie il nodo con 2 aste e 1 forza applicata e di seguito si risolvono gli altri nodi. E' necessario fare l'equilibrio al nodo considerando anche il contributo orizzantale o verticale dato dalla scomposizione delle aste inclinate.

esempio

Per quanto riguarda invece il METODO DELLE SEZIONI DI RITTER si sceglie di dividere via via la struttura con una sezione di ritter appunto, ovvero tagliando 3 aste convergenti nello stesso nodo. In tal modo avremo 3 equazioni in 3 incognite che saranno gli sforzi normali delle aste tagliate. La regola consiste nello scrivere le equazioni di equilibrio a rotazione, cambiando ogni volta il polo. Inizialmente nell'equazione di equilibrio del momento viene scelto il punto di incontro di 2 delle 3 aste in modo da avere una sola forza incognita. Successivamente sposto il polo e trovo la seconda incognita e infine per la terza posso applicare l'equazione alla traslazione verticale o orizzontale nel nodo. Qualora il risultato delle incognite sia positivo allora l'asta sarà un tirante, negativo sarà un puntone.  

ESERCITAZIONE SULL'EQUAZIONE DELLA LINEA ELASTICA

Quando ci troviamo di fronte ad una struttura iperstatica, ovvero il numero dei gradi di libertà è inferiore al numero dei gradi di vincolo (nl<nv), non è facile determinare nè le reazioni vincolari nè le azioni di contatto poichè le incognite sono superiori al numero di equazioni di bilancio. Si ricorre quindi a metodi come quello degli spostamenti o equazione della linea elastica.

Partendo da tutte le equazioni del modello di trave di Bernoulli, le distinguiamo in 3 gruppi:

EQUAZIONI DI EQUILIBRIO (mostrano il legame tra carichi esterni e sollecitazioni)

EQUAZIONI DI CONGRUENZA (mostrano il legame tra deformazioni e spostamenti)

LEGAME COSTITUTIVO (mostrano il legame tra deformazioni e sollecitazioni)

Ci concentriamo successivamente sul problema flessionale, distinguendolo da quello assiale e di conseguenza ci occuperemo solo delle seguenti grandezze e relative equazioni:

φ, ν, χ, M, T

Nel metodo della linea elastica le incognite sono le funzioni spostamento e rotazione della trave e gli strumenti risolutivi sono equazioni differenziali dove bisogna effettuare successive operazioni di integrazione. La diffcicoltà è nel riconoscere le condizioni al bordo.