Esercitazione sul Graticcio

GRATICCIO DI TRAVI

Il Graticcio di travi, utilizzato per grandi luci, è costituito da travi dirette lungo due direzioni perpendicolari. Si differenzia dalla gerarchia di travi perché non è costituito da travi principali e travi secondarie, ma tutte le travi collaborano allo stesso modo, hanno lo stesso momento di inerzia a prescindere dalla loro orditura e presentano un nodo che consente la trasmissione della rotazione .

RISOLUZIONE DI UN GRATICCIO

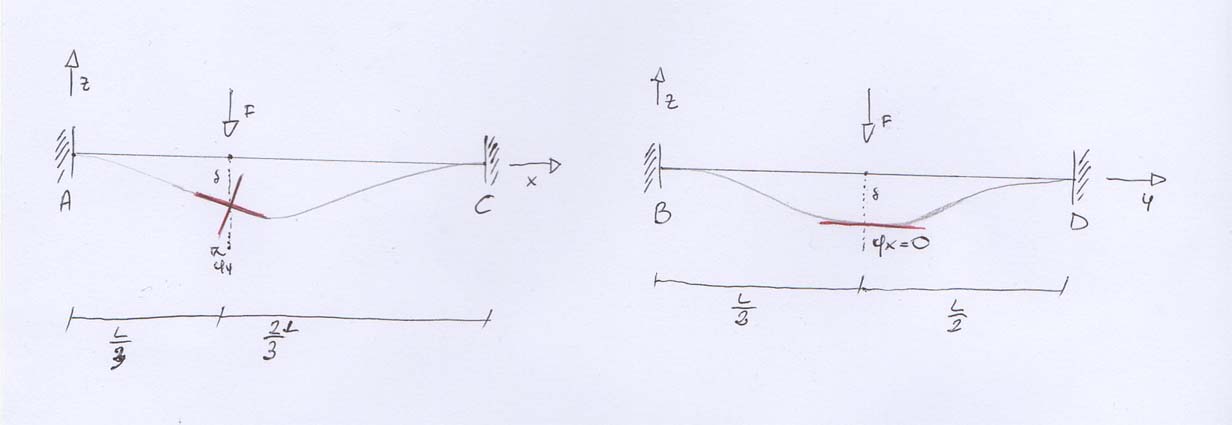
L’esercizio propone 2 travi entrambe doppiamente incastrate, su cui agisce una forza F all’incrocio tra le 2 aste. Il nodo in 3 d ha 6 gradi di libertà: esso può avere 3 differenti traslazioni, secondo i 3 assi x, y e z e 3 rotazioni intorno ai 3 assi. Analizziamo le deformate delle due aste separatamente e notiamo che:

SPOSTAMENTI

Per l’indeformabilità delle aste, che altrimenti si accorcerebbero o allungherebbero, non abbiamo spostamenti lungo x e lungo y,(u_x u_y =0), ma solamente lungo z ( u_z =delta)  a causa del carico F che agisce lungo z.

ROTAZIONI

φ_z non la consideriamo, φ_x è nulla poiché nell’asta BC la forza F  è applicata a l/2  dove la tangente è orizzontale,φ_y è l’unica ad esserci.

Le incognite sono quindi: lo spostamento (∂) e la rotazione (φ_y) che troveremo attraverso 2 equazioni di equilibrio al nodo:

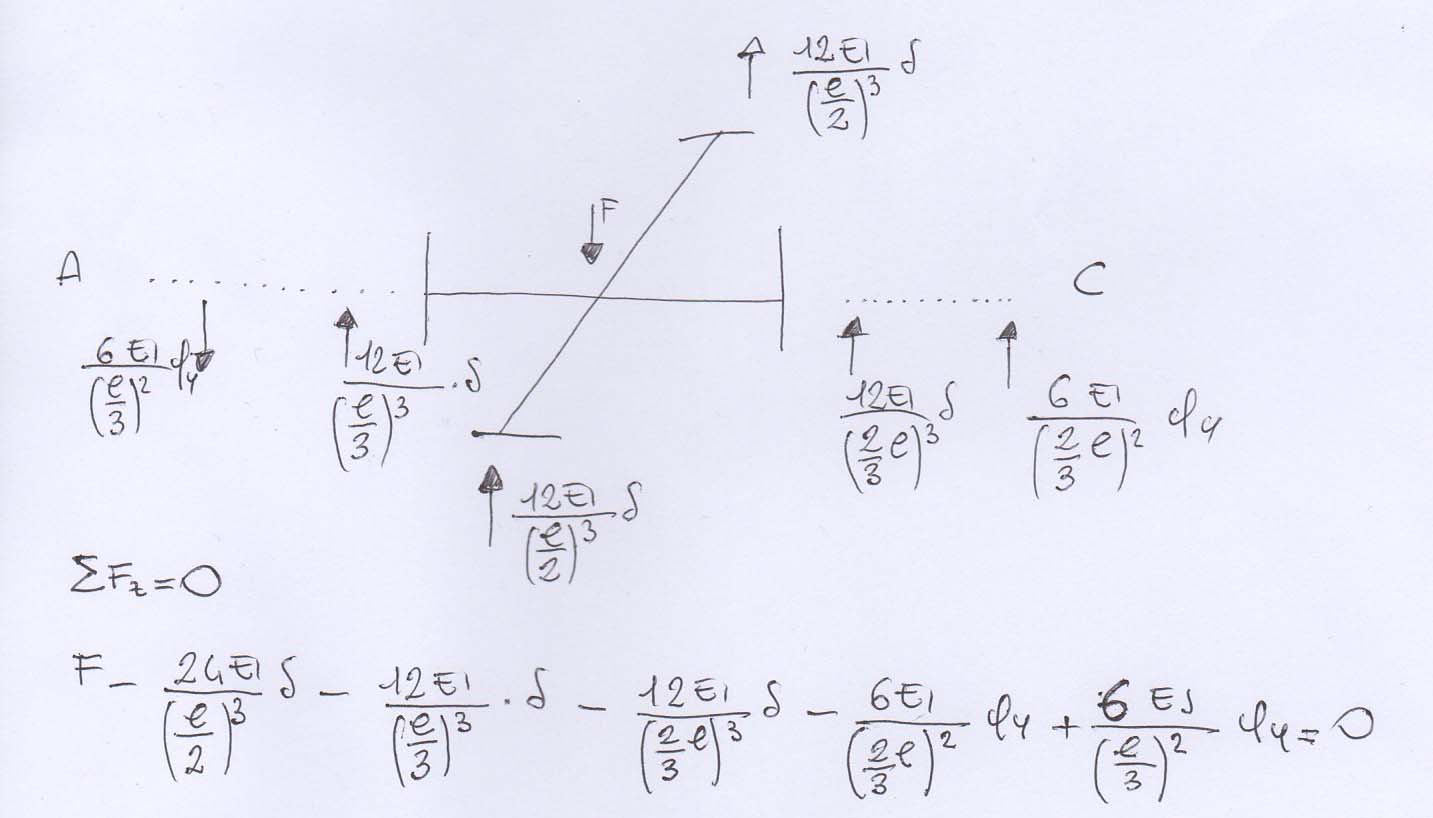
Equilibrio CONTRO la traslazione verticale           

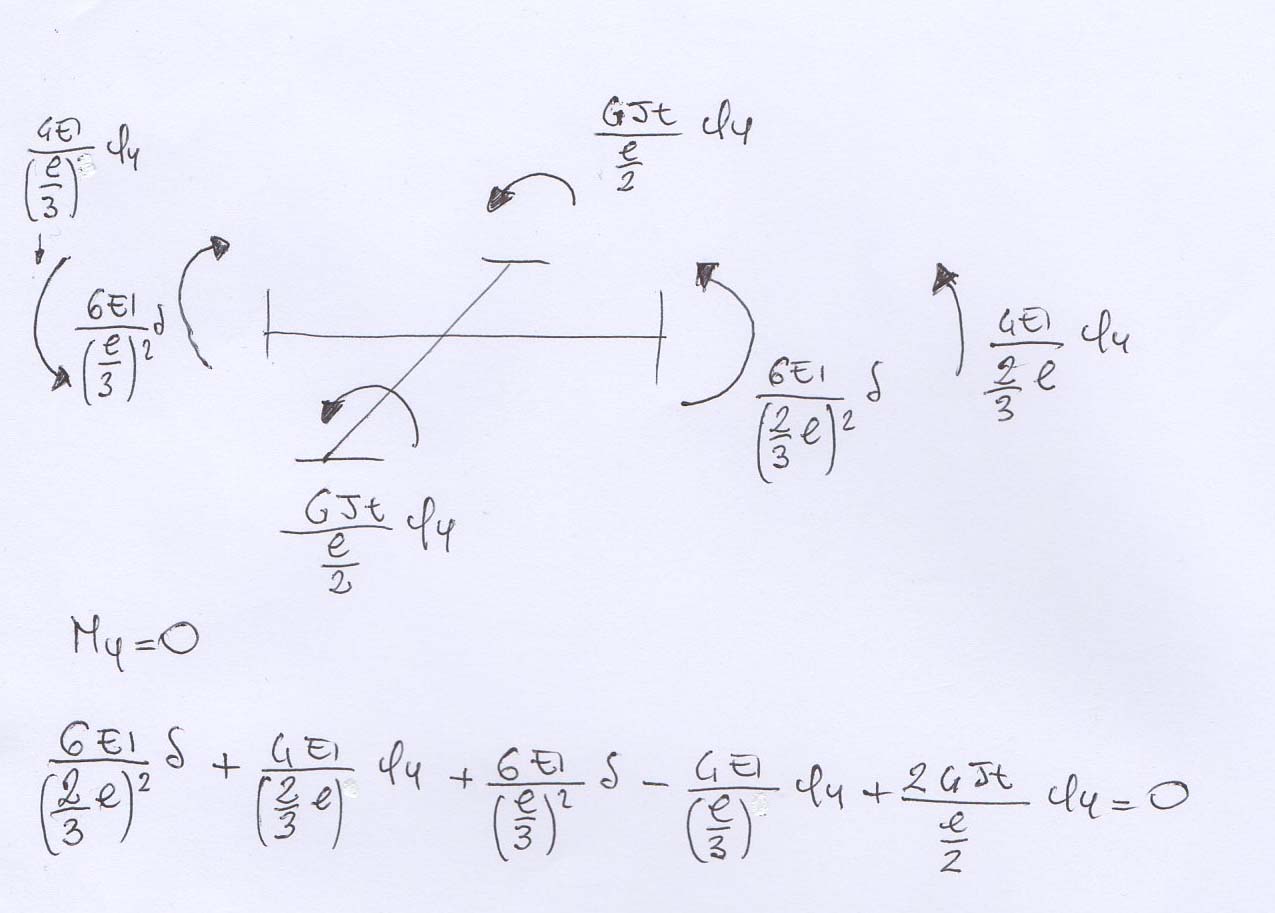
Equilibrio CONTRO la rotazione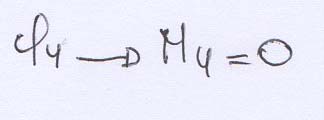                              

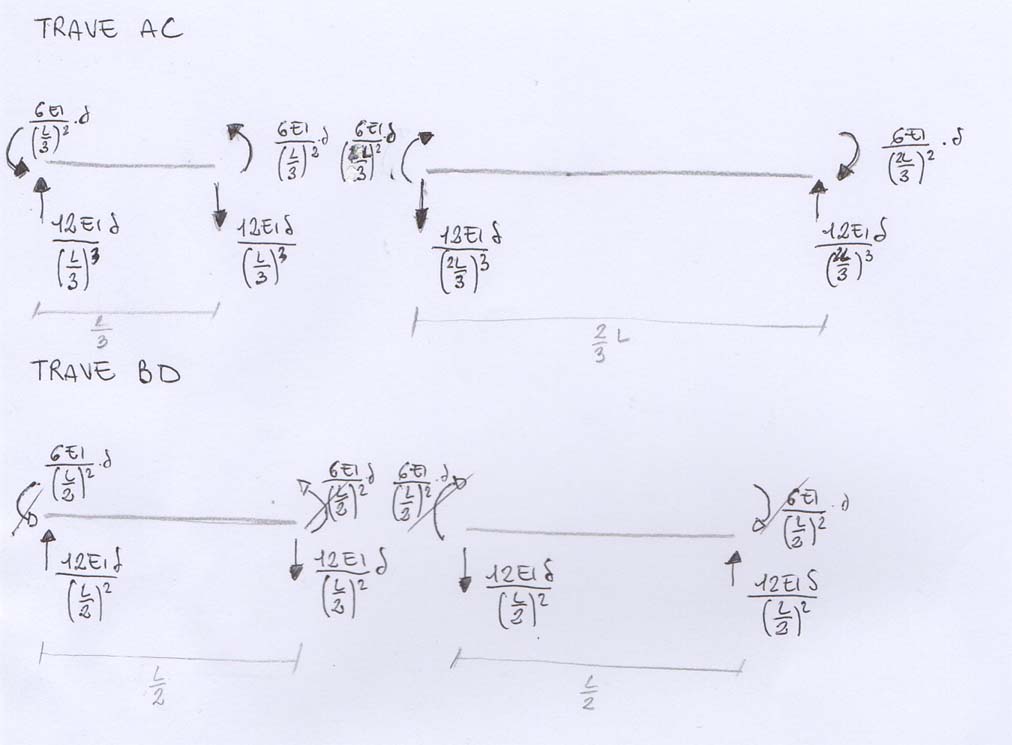
Separiamo idealmente le due incognite, facendole agire separatamente e sovrapponendone poi gli effetti. Conoscendo i valori in una trave doppiamente incastrata possiamo quantificare Taglio e Momento flettente. 

Analizzando solo i gli effetti di ∂ vediamo:

Analizzando solo i gli effetti della rotazione oraria φ_yvediamo:

deformazioni, reazioni vincolari e momenti

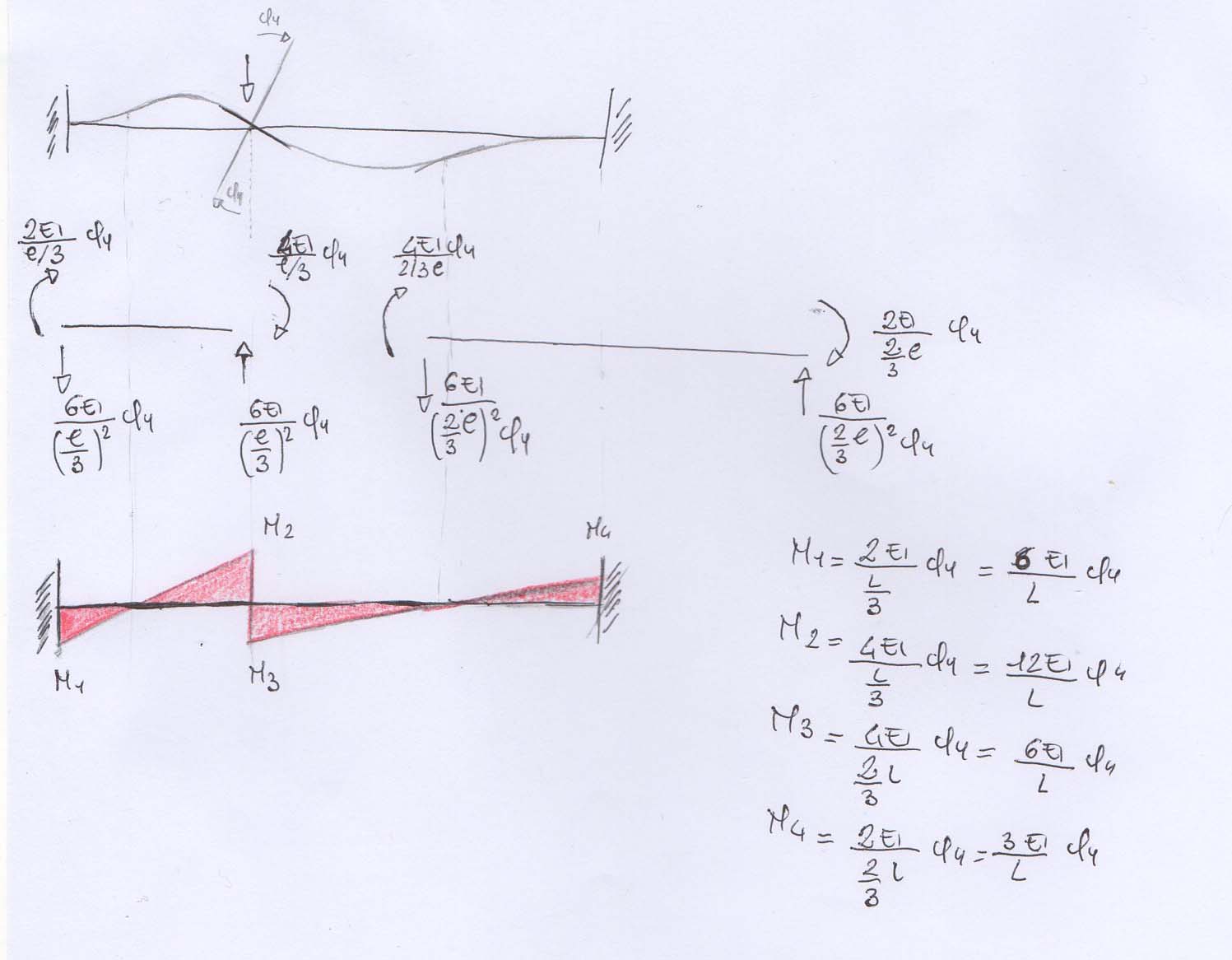
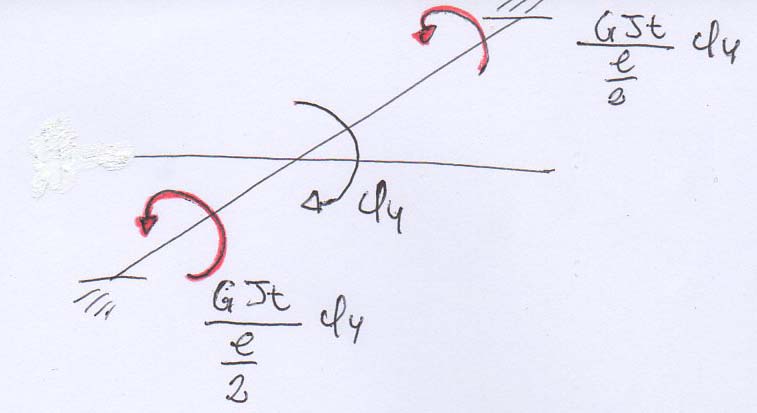
La flessione della trave AC intorno all’asse y provoca la torsione di quella BD poiché ciò che è flessione in un piano diventa torsione nel piano ortogonale a questo.

EQUILIBRIO AL NODO CONTRO LA TRASLAZIONE VERTICALE

EQUILIBRIO AL NODO CONTRO LA ROTAZIONE INTORNO ALL’ASSE Y

Per trovare il valore dello spostamento e della rotazione, inseriamo i valori noti

Per una luce l=6 m e una forza F=20 KN e entrambe le aste hanno una sezione rettangolare in cls con a=0,67m e b=0,15m

Otteniamo i seguenti valori:

Verifico i risultati ottenuti con sap.

Disegno attraverso una griglia il graticcio in sap, gli assegno il materiale, la sezione scelta precedentemente, il modulo di elasticità e di elasticità tangenziale.

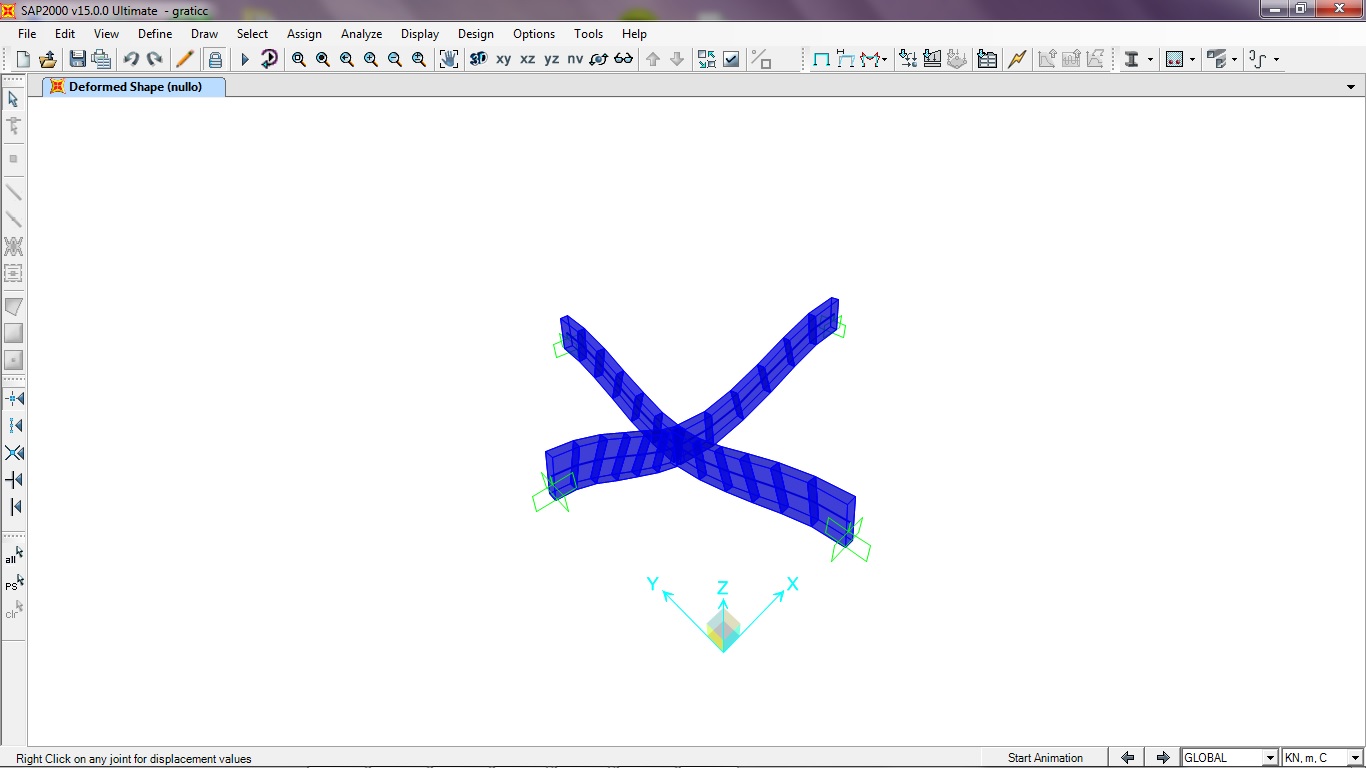
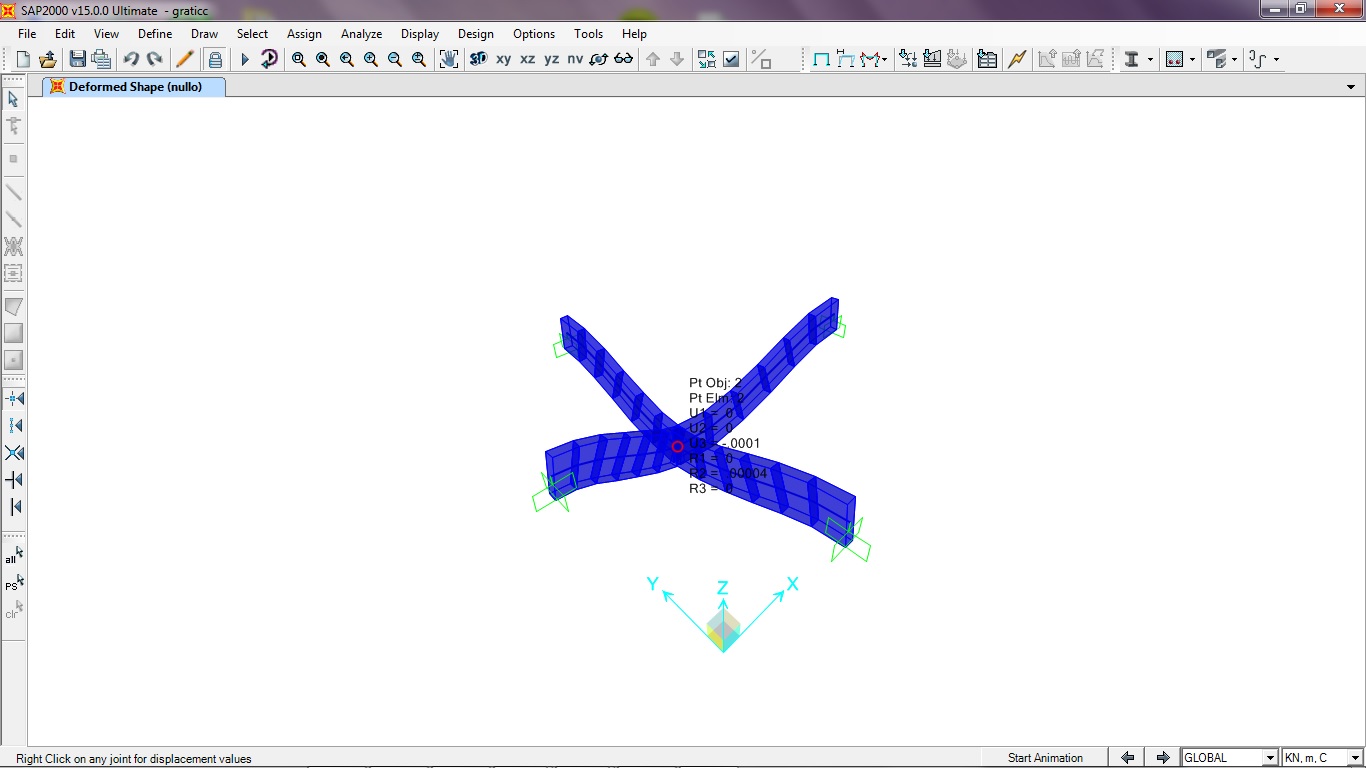
Notiamo che anche con sap ho trovato gli stessi valori per le rotazioni e gli spostamenti.

Otteniamo i seguenti valori:

u₃=u_z =0,0001 con segno negativo perché convenzionalmente l’asse positivo è verso l’alto

R₂= φ_Y = 0,00004