Esercitazione sulla Trave di Vierendeel

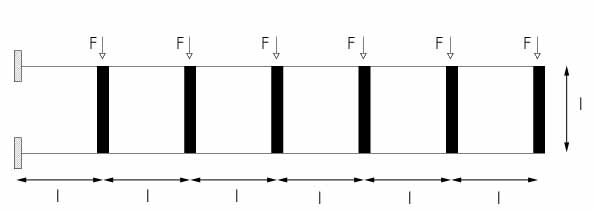
La TRAVE VIERENDEEL si comporta coma un telaio shear type ribaltato, per cui, presenta pilastri infinitamente rigidi e traversi flessibili. Ne deriva che la forza (F) fa traslare il ritto di una quantità δ, trascinando con sé i traversi che si deformano.

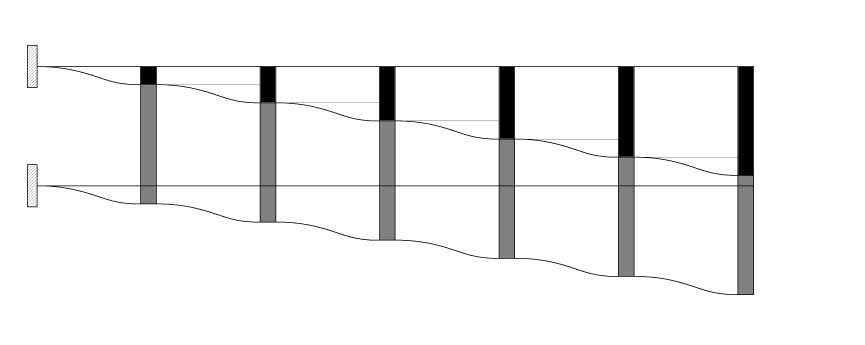
La presenza dei nodi incastro e l’ipotesi di rigidezza flessionale infinita dei pilastri, impone però ai nodi una rotazione nulla. Il traverso si trova nella situazione di una trave doppiamente incastrata  con un sistema che è tre volte iperstatico. Supponendo che uno dei due incastri ceda, avviene una deformazione e quindi una curvatura.

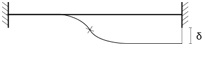
Per sapere quanto valgono taglio e momento risolvo la struttura iperstatica con il metodo della linea elastica.

Ottengo quindi i seguenti valori:

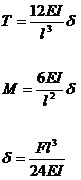
Dalle equazioni di equilibrio alla traslazione verticale dei pilastri posso risalire agli spostamenti, ai tagli e ai momenti.

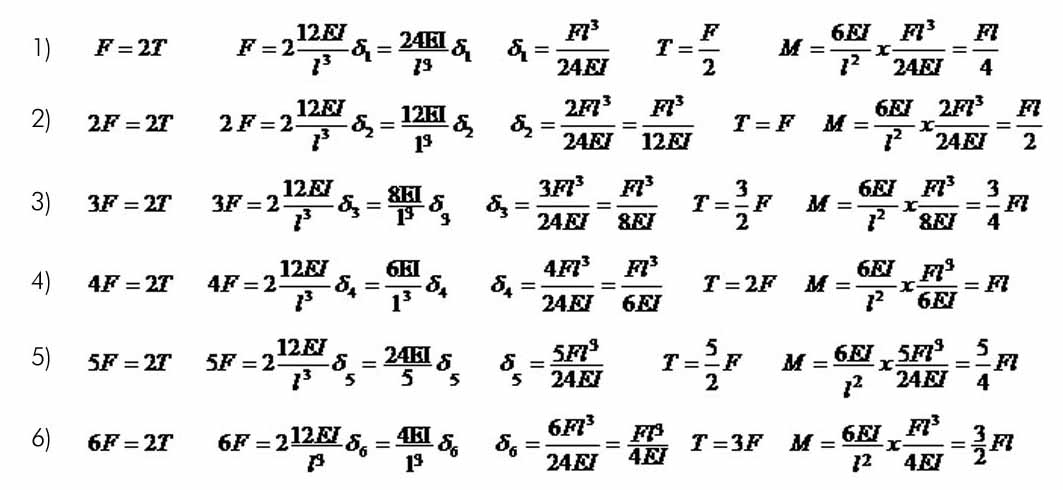
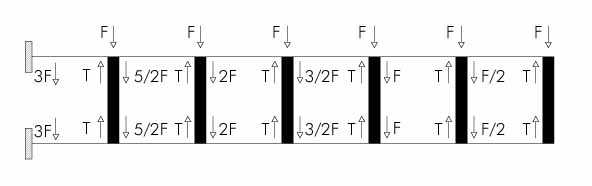
DIAGRAMMA TAGLIO dei TRAVERSI

DIAGRAMMA MOMENTI dei TRAVERSI

Più semplicemente si potevano conoscere i valori del taglio e del momento facendo pochi calcoli. Per il taglio bastava sommare tutte le forze agenti sulla trave e successivamente dividerli per due. Per il momento,osservando la deformata si vede dove la curvatura è nulla e quindi anche il momento è nullo. Basta moltiplicare quindi la forza di taglio per il suo braccio l/2 per avere i valori dei momenti.

Per conoscere i valori del momento su ogni pilastro, calcolo l’equilibrio in ogni nodo.

Mpilastro=M1+M2(se sono entrembi orario producono un momento nei pilastri antiorario)

Per il taglio nei pilastri applico la seguente regola: 

e quindi ottengo per tutti i pilastri i seguenti valori:

DIAGRAMMA TAGLIO dei PILASTRI

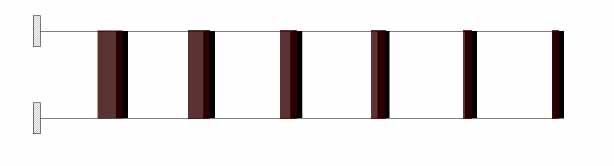
DIAGRAMMA MOMENTO dei PILASTRI

VERIFICA CON SAP

Disegno la trave vierendeel a sbalzo di L =10 m attravarso la griglia, gli assegno i 2 vincoli di incastro, il peso nullo alla struttura e le forze applicate in z all'incrocio tra travi e pilastri pari a -10 KN m.

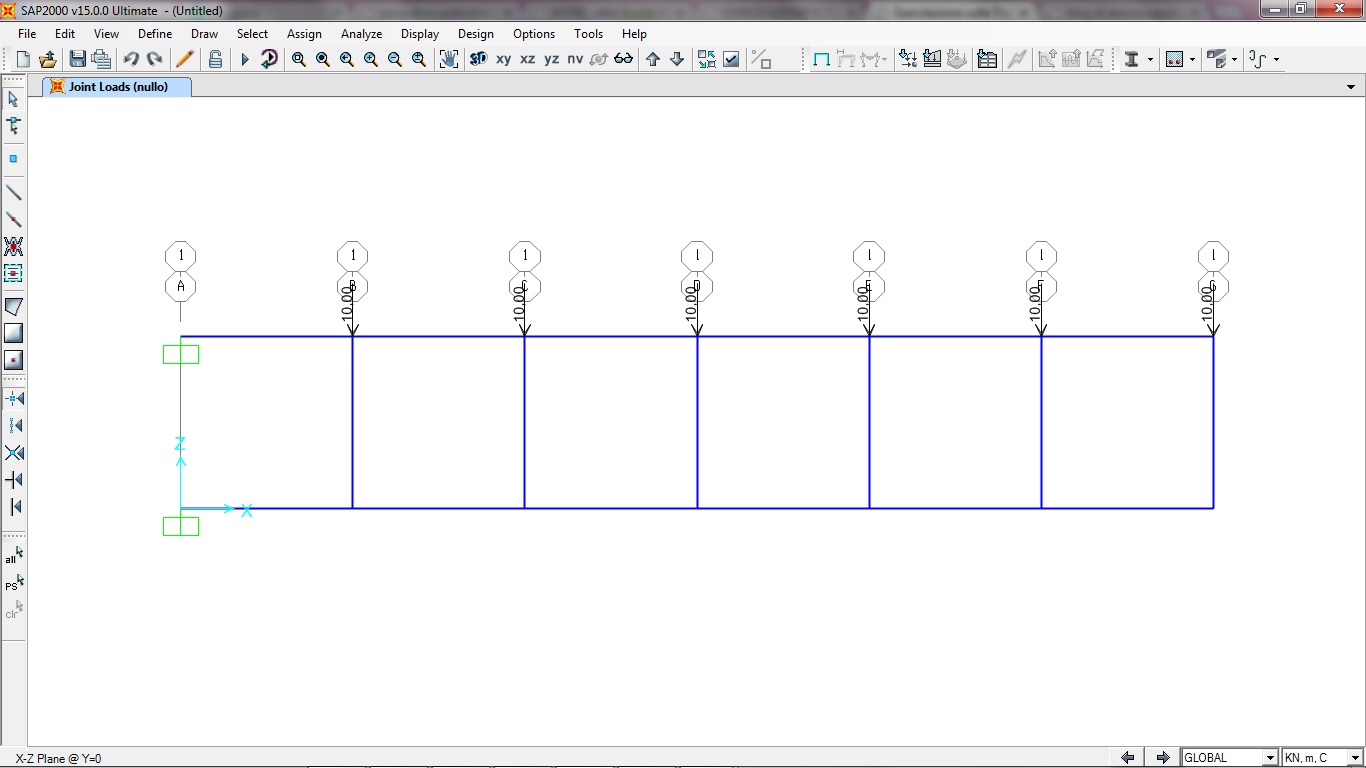
Successivamente per poter avere un comportamento simile a quello della trave vierendeel devo assegnare ai pilastri una rigidezza infinita. Su Sap ciò si può ottenere o dando ai pilastri una sezione con modulo di elasticità molto alto oppure assegnandogli una sezione molto grossa. Scelgo la seconda opzione.

Assegno ai traversi una sezione di questo tipo:

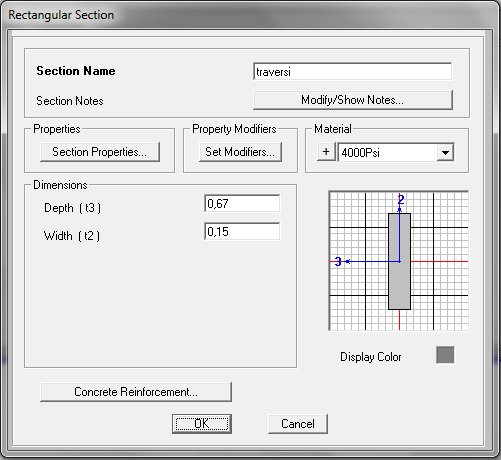
e ai RITTI una sezione di questo tipo:

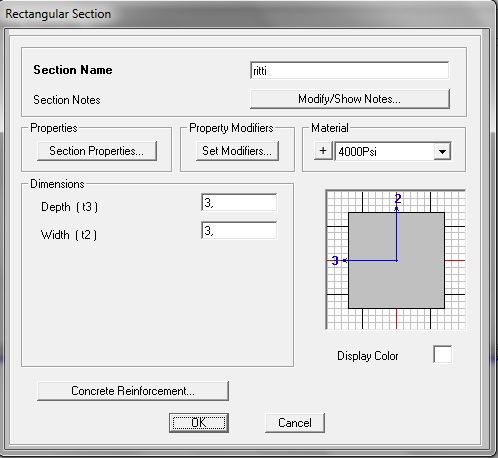
Per ottenere delle sezioni di questo tipo

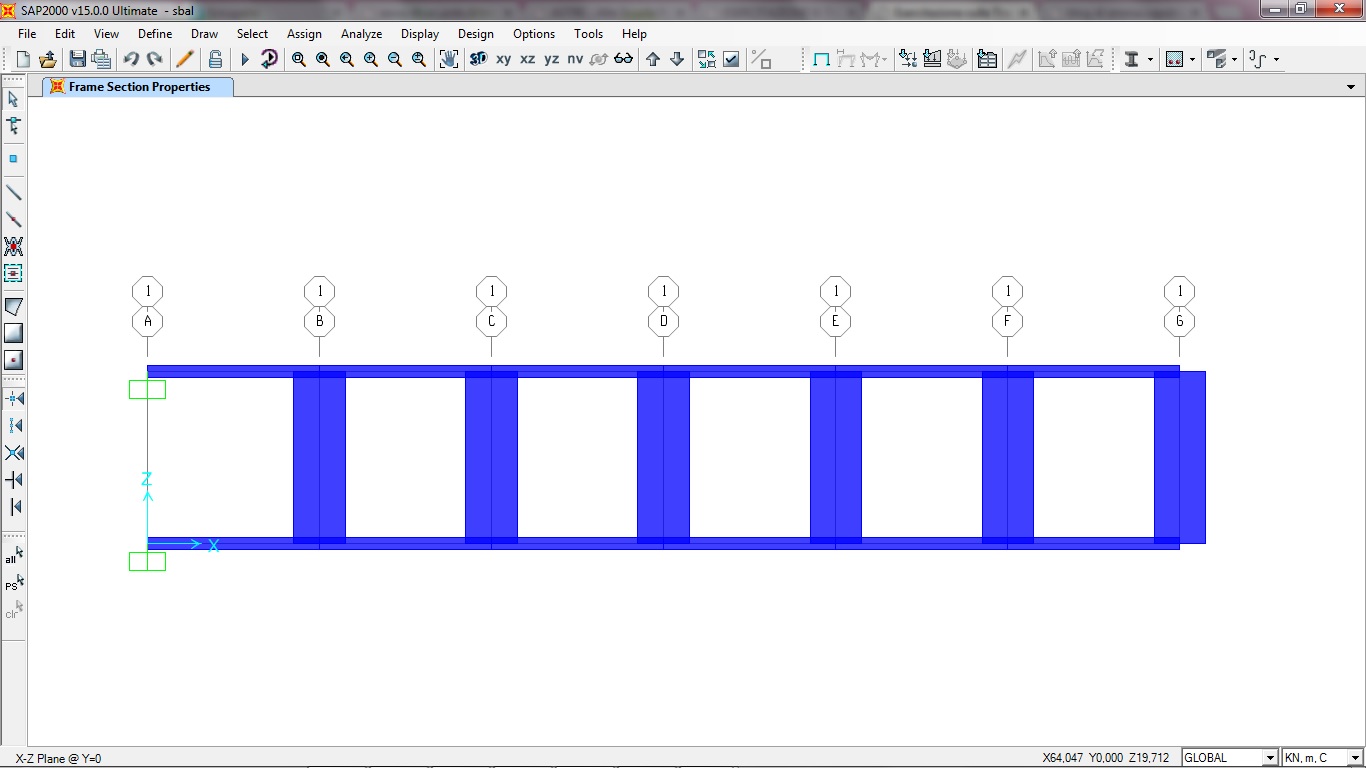
Faccio partire l'analisi con Run e ottengo:

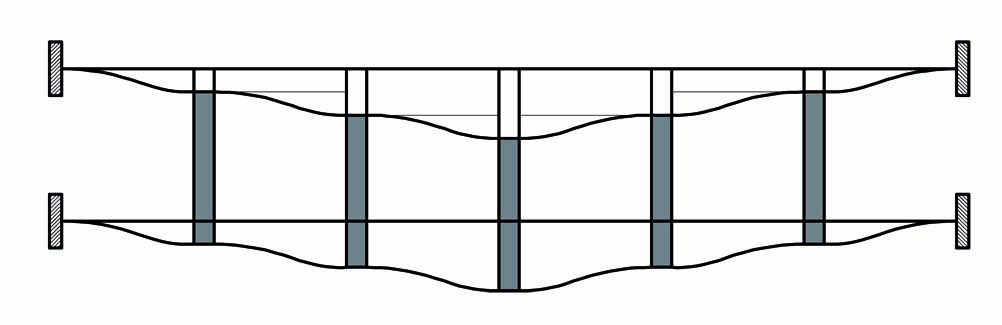
DEFORMATA

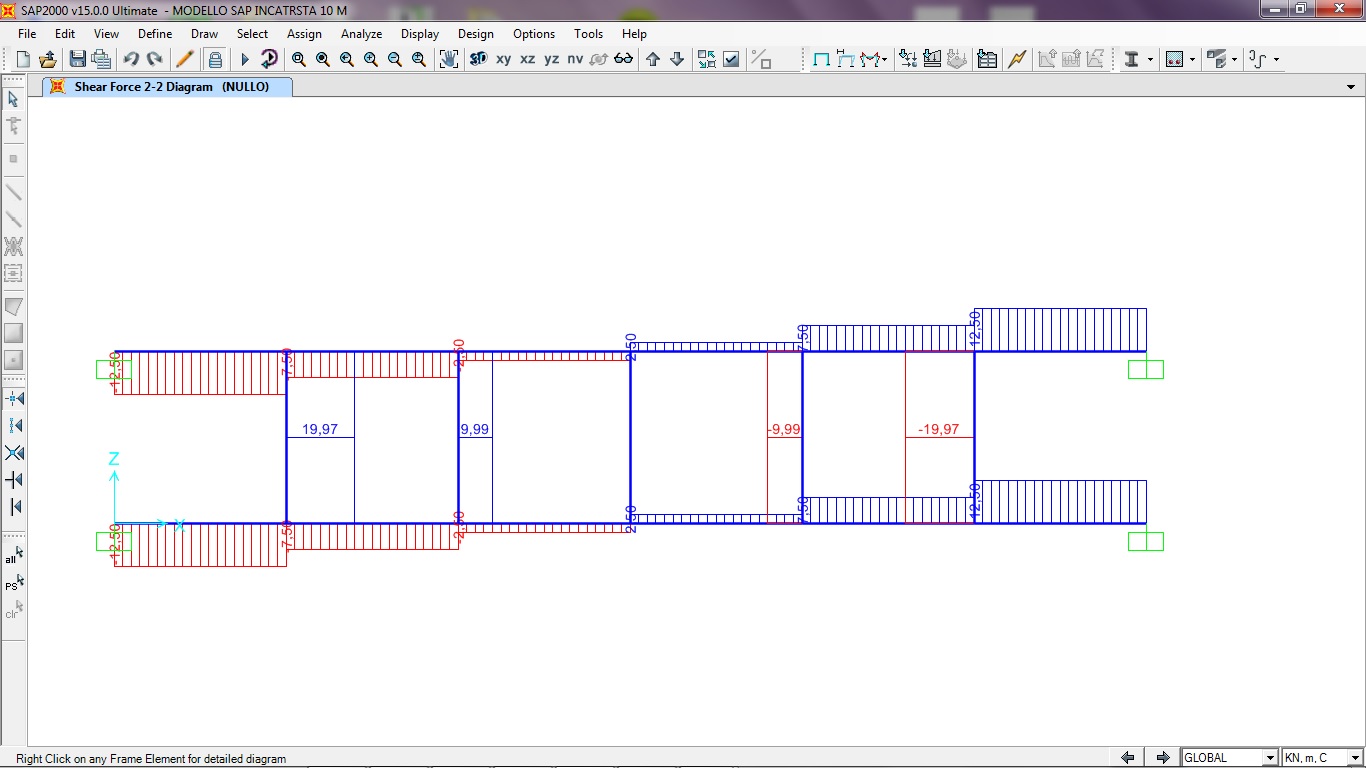
DIAGRAMMA TAGLIO

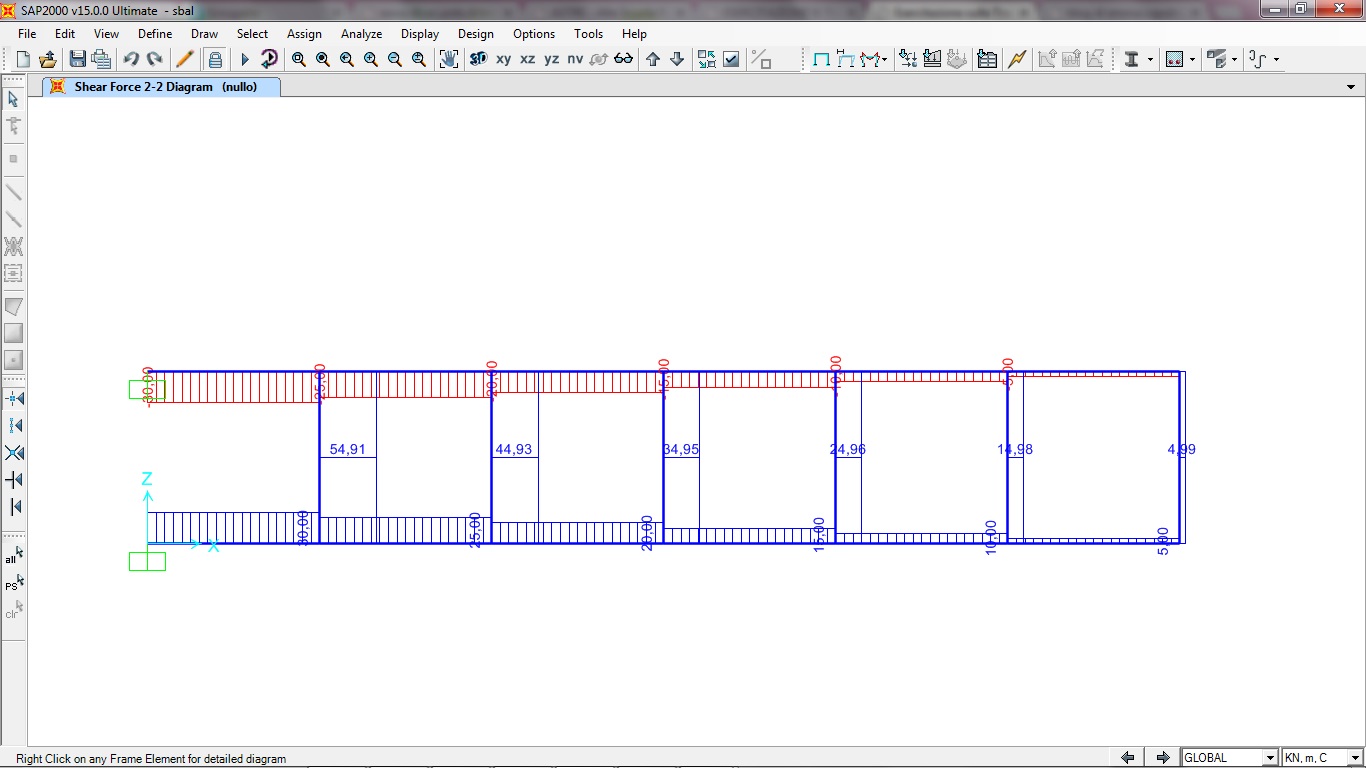
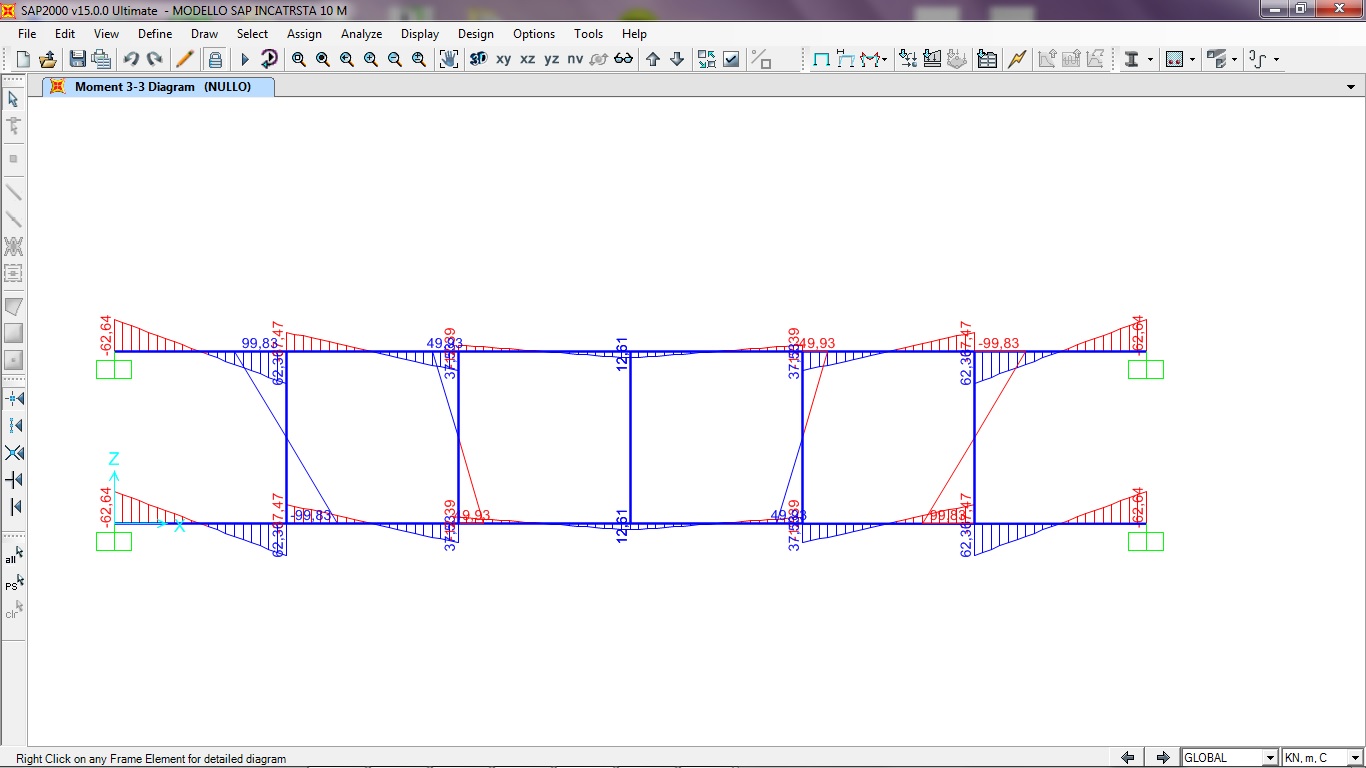
DIAGRAMMA MOMENTO

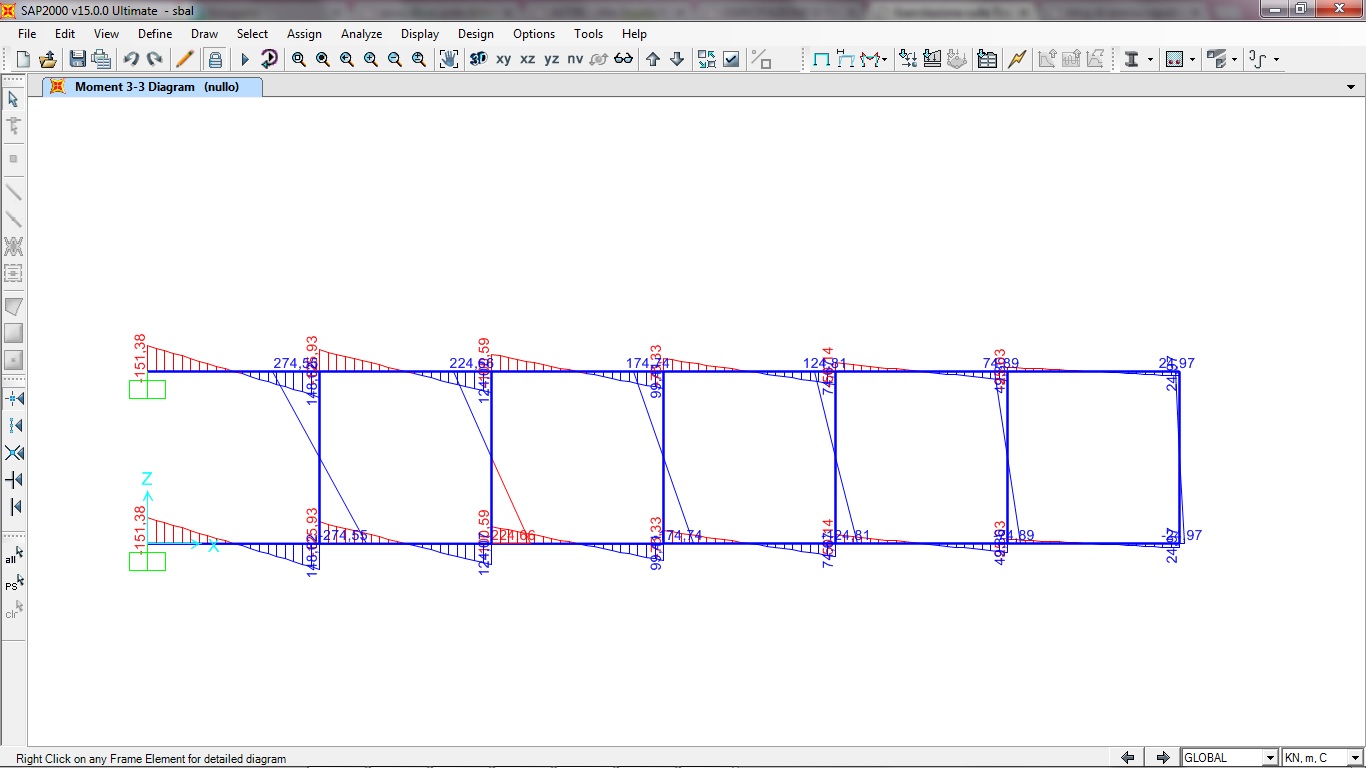
TRAVE VIERENDEEL DOPPIAMENTE INCASTRATA

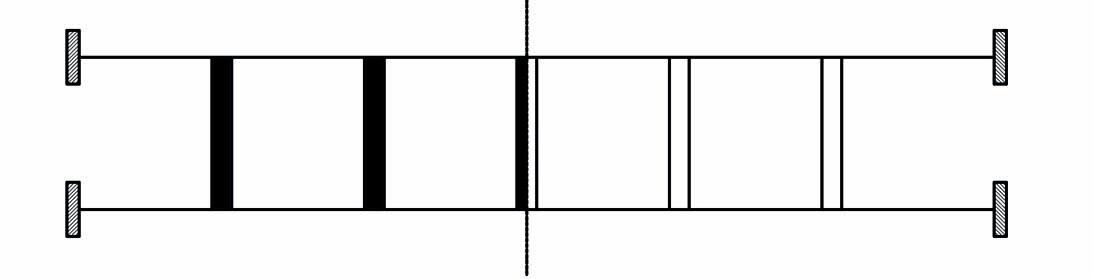
DEFORMATA

Essendo una struttura simmetrica ne analizzo solamente la metà.

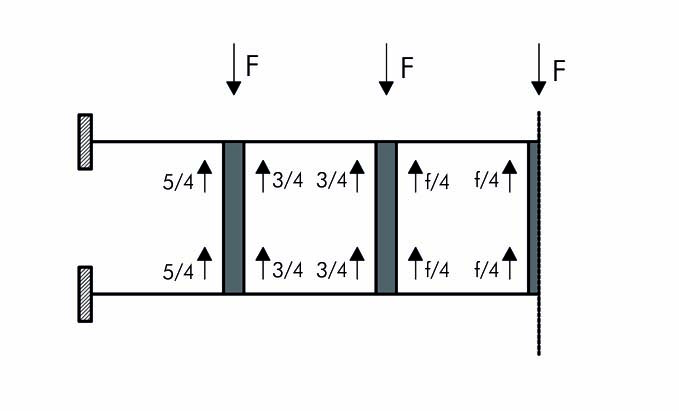
EQUILIBRIO AI NODI

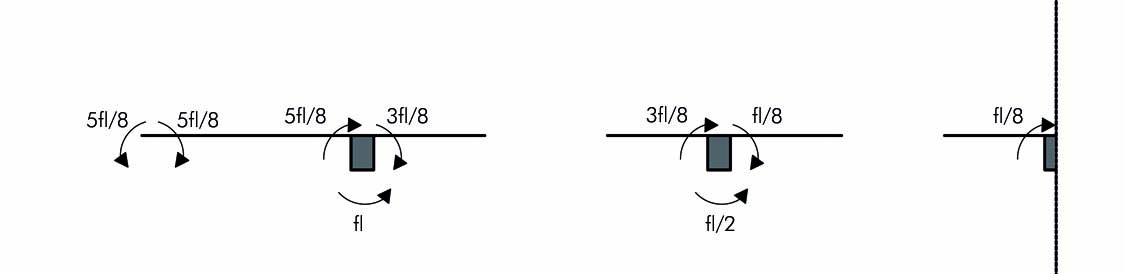
DIAGRAMMA MOMENTI

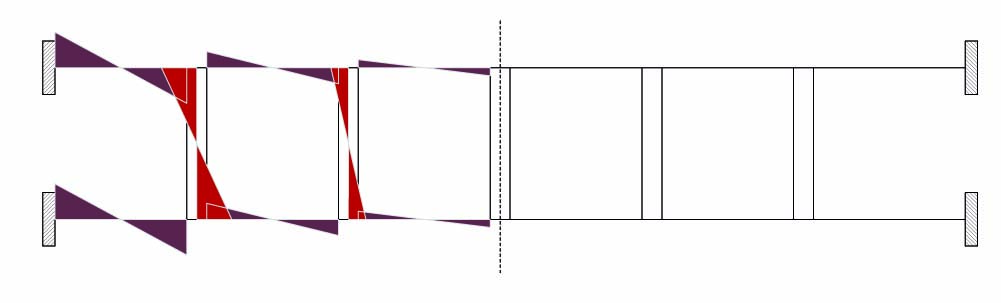
Analizzandola con SAP, ottengo i seguenti risultati: