Esercitazione4-Risoluzione trave iperstatica (metodo delle forze)

L’esercitazione questa volta richiede di risolvere un sistema iperstatico e quindi di trovare i valori di Momento e Taglio per ogni sezione della struttura in studio.

L’iperstaticità indica che un corpo ha più vincoli rispetto ai suoi gradi di libertà. Per risolvere una struttura del genere si può usare un metodo chiamato “delle forze”, in cui si trasformano i vincoli in modo da riportare l’asta ad un sistema isostatico e restituendo i vincoli levati sottoforma di forza contrastante il movimento che il vincolo bloccava.

I vincoli perciò devono essere declassati. Ma come riconoscere i vincoli da declassare e quali no? In base alla conoscenza acquisita riguardo ai valori di abbassamento e rotazione nelle condizioni di carico si capisce quale è il vincolo da dover togliere in modo che il movimento dell’asta potrà essere riconducibile a quello di una struttura isostatica. Nel nostro caso il sistema migliore è quello di cambiare i 3 vincoli interni da cerniera esterna a cerniera interna a B, C e D.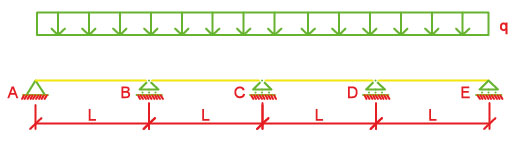 

Il sistema ora è diventato isostatico ma differisce rispetto a quello di partenza. Per riportarlo allo stato originario ma mantenendo il nuovo vincolo dato basta aggiungere una reazione di momento, che chiameremo x₁ x₂ x₃, alle cerniere interne in modo da ristabilire il vincolo che indica che la parte a destra e a sinistra della cerniera non ruotino ma rimangano come un singolo elemento.

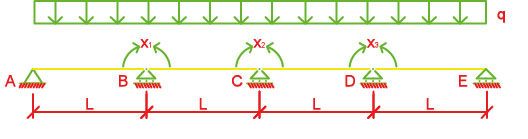
In questo caso noi siamo già a conoscenza del valore di rotazione dell’asta isostatica quindi è abbastanza agevole la risoluzione del sistema.

Grazie alla simmetria della struttura posso porre x₁=x₃.

A questo punto sappiamo che la rotazione nelle cerniere deve essere uguale a zero e possiamo quindi scrivere l’equazione di compatibilità cinematica: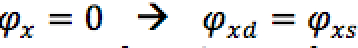 

Sostituendo i valori dei momenti ai nodi nell’equazione e mettendo a sistema le corrispondenti equazioni contenenti x1 e x2 otterròi due risultati:

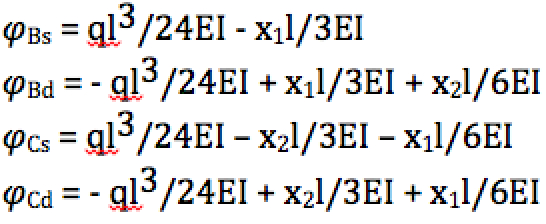
eguaglio

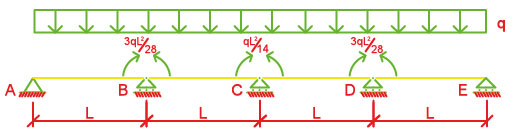
Una volta saputi i valori di x₁ ed x₂ applico il principio di sovrapposizione degli effetti e quindi studio la struttura dividendola in due schemi: uno dipendente dal carico q e l’altro dipendente dalle reazioni vincolari x.

q)

x)

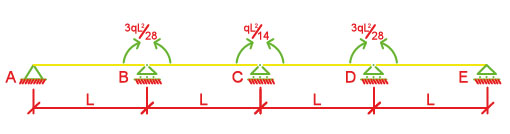
In tutti e due i casi posso scomporre la struttura in 4 aste isostatiche doppiamente appoggiate e andare a studiare le reazioni vincolari e quindi sommarli tra loro.

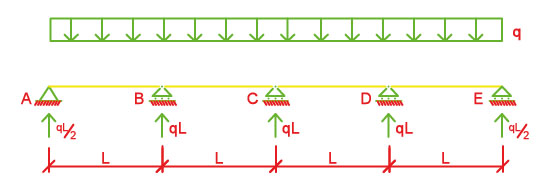
q)

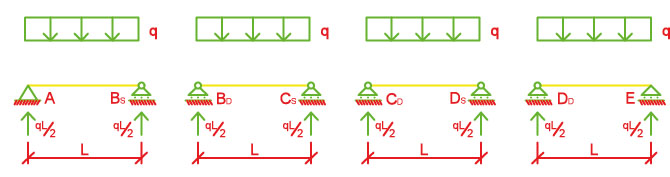
x)

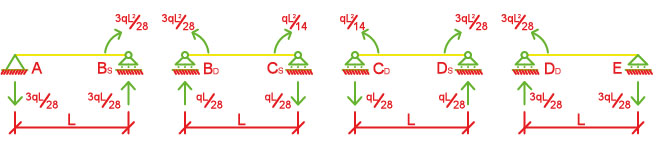
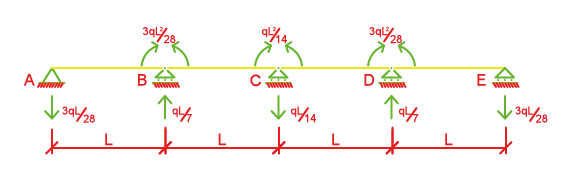
Dopo aver trovato finalmente le reazioni vincolari sovrappongo i due sistemi di reazioni e avere lo schema delle reazioni vincolari della nostra trave iperstatica di partenza.

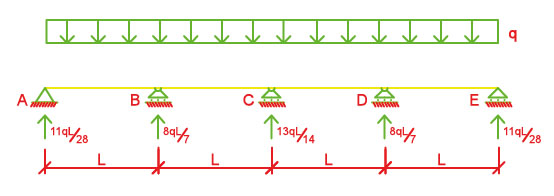
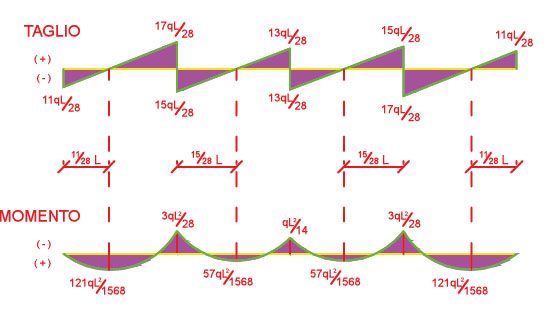
Disegnamo ora i grafici di Taglio e Momento.