Esercitazione METODO DELLE FORZE

Il Metodo delle Forze

Il Metodo delle forze viene utilizzato per la risoluzione di strutture iperstatiche e si adatta perfettamente al caso di strutture iperstatiche composte da travi come la tave singola, la trave continua su più appoggi.

Il metodo si articola in quattro passi:

1.     la scelta di una struttura isostatica di riferimento e l’individuazione delle incognite iperstatiche.

2.     la scrittura delle equazioni di compatibilità cinematica.

3.     la risoluzione del sistema di equazioni per la determinazione delle incognite iperstatiche.

4.     la sistematica applicazione del principio di sovrapposizione degli effetti per la determinazione delle azioni di contatto sulla struttura iperstatica.

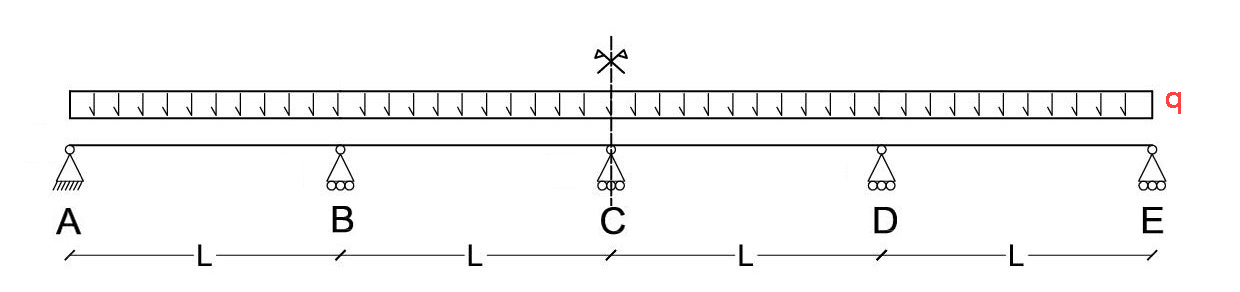
Trave continua su cinque appoggi_ La trave è 3 volte iperstatica

GDV= 6 

GDL= 3

1.     scelta di una struttura isostatica di riferimento e l’individuazione delle incognite iperstatiche.

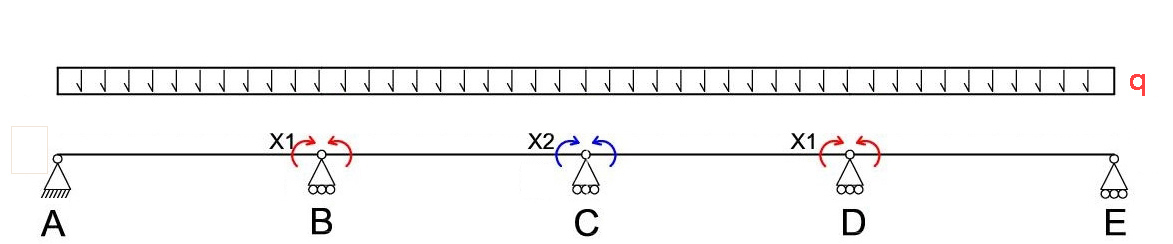
Scelgo una struttura  isostatica di riferimento. Trasformo le cerniere in B, C e D in cerniere interne applicando dei momenti X1, X2. Essendo la trave simmetrica nel punto C posso applicare X1 anche in D. Le incognite sono X1e X2.

Trattare una trave continua su più appoggi come un insieme di travi appoggiate rende più semplice la soluzione del problema iperstatico.

2.     la scrittura delle equazioni di compatibilità cinematica.

Per ripristinare le condizione di vincolo di continuità della trave devo imporre le equazioni di compatibilità cinematica, la rotazione relativa nei punti sia a sinistra (S) che a destra (D)  in cui ho rimosso il vincolo:

ΔφB = 0 

φBS – φBD = 0

φBS = ql³/24EJ – X1l/3EJ

φBD = - ql³/24EJ + X1l/3EJ + X2l/6EJ

ΔφC = 0 

φCS – φCD = 0

φCS = + ql³/24EJ - X2l/3EJ – X1l/6EJ

φCD = - ql³/24EJ + X2l/3EJ + X1l/6EJ

ΔφB = ΔφC

3.    la risoluzione del sistema di equazioni per la determinazione delle incognite iperstatiche.

Consideriamo i seguenti tratti:

Troviamo le incognite X1e X2:

ΔφB = 0  

φBS – φBD = 0

ql³/24EI - X1L/3EI+ ql³/24EI - X1L/3EI - X2L/6EI=0

2ql³/24EI - 2X1L/3EI - X2L/6EI=0

X2/2 = -2X1+ ql²/4

X2= -4X1+ ql²/2     

ΔφC = 0 

φCS – φCD = 0

ql³/24EI – X2l/3EI - X1l/6EI+ ql³/24EI - X2l/3EI - X1l/6EI=0

2ql³/24EI – 2X2l/3EI - 2X1l/6EI=0

-X1/2 = X2 - ql²/8  

X1= - 2X2- ql²/4    sostituisco in ΔφB = 0 

X2= -4(-2X2- ql²/4)+ ql²/2    

X2= 8X2- ql² + ql²/2   

ql² - ql²/2 = 7X2

X2= ql²/14

X1= 3/28 ql²

4.   la sistematica applicazione del principio di sovrapposizione degli effetti per la determinazione delle azioni di contatto sulla struttura iperstatica.

Trovate le incognite X1 e X2 posso cercare le reazioni vincolari:

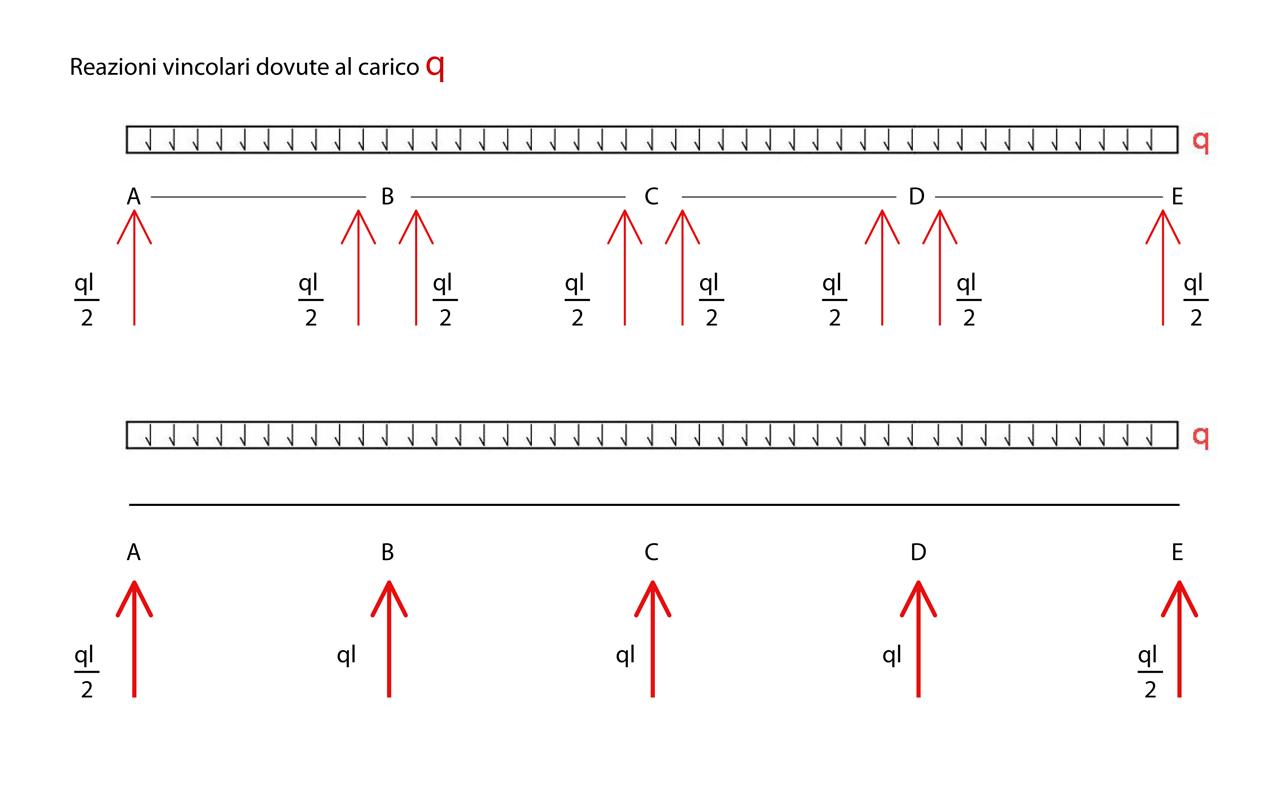
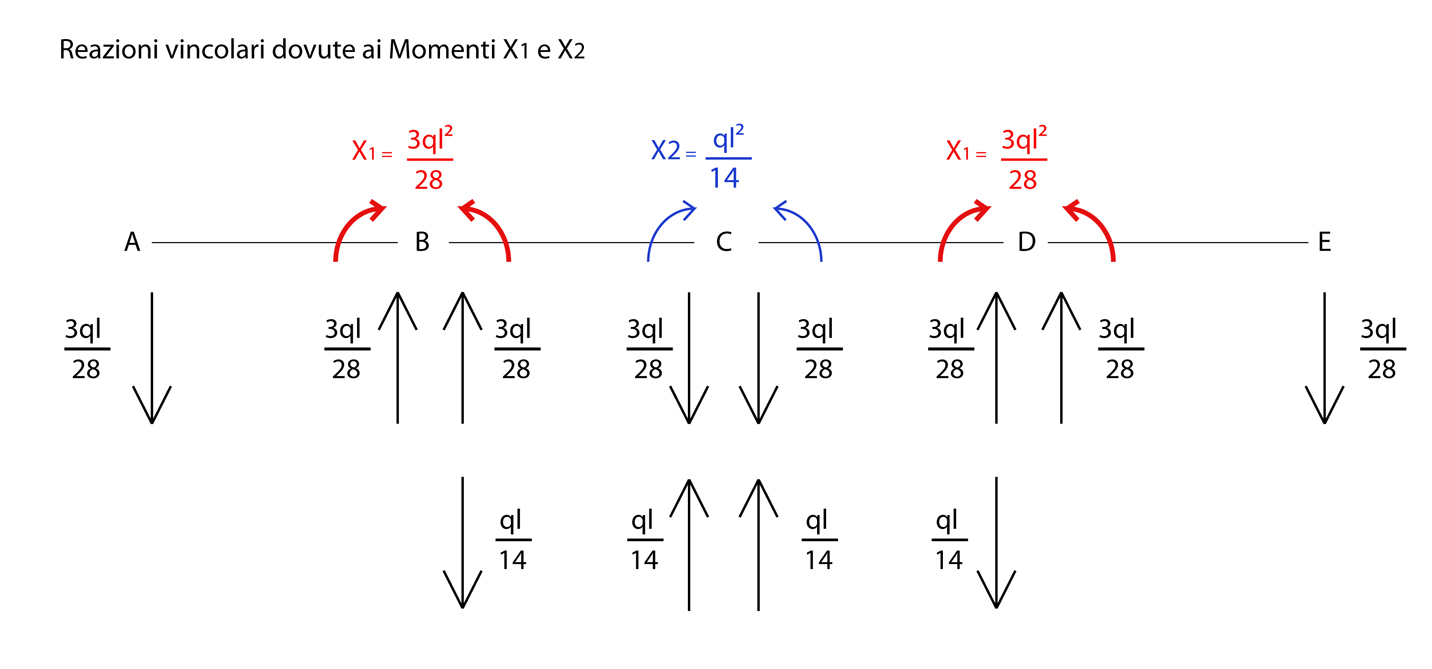
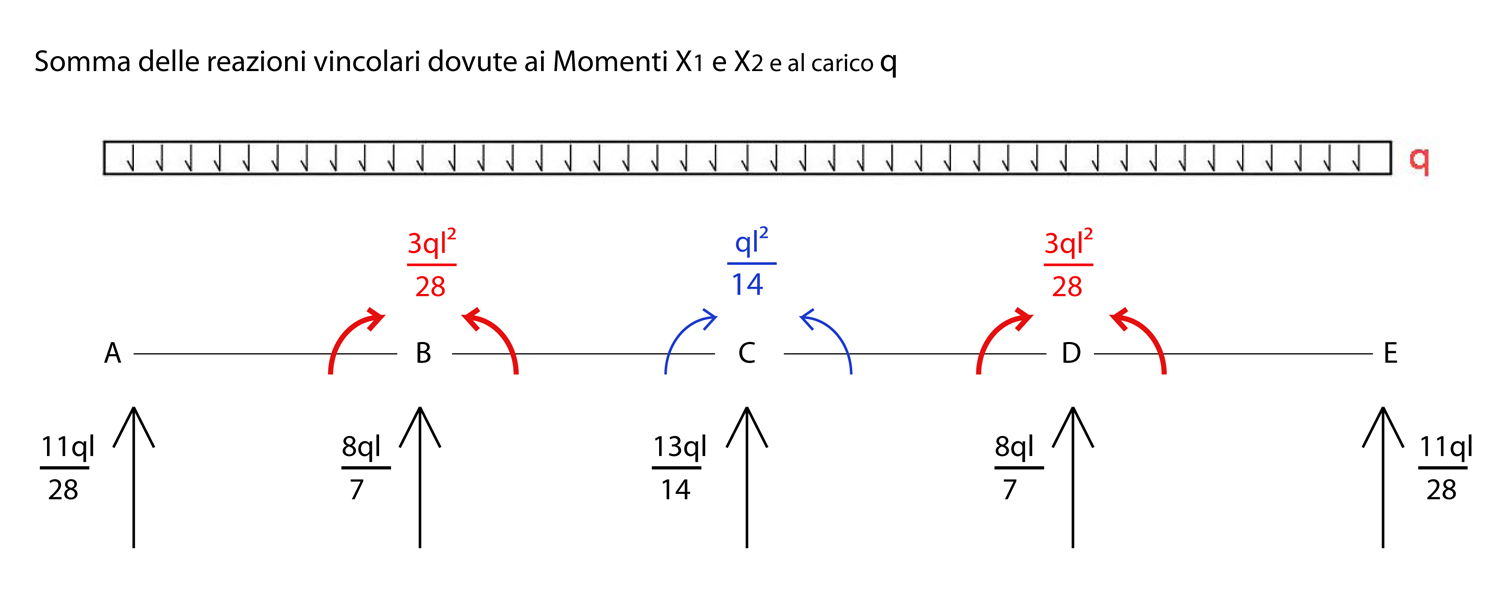
Sommiamo q con il momento in ogni punto:

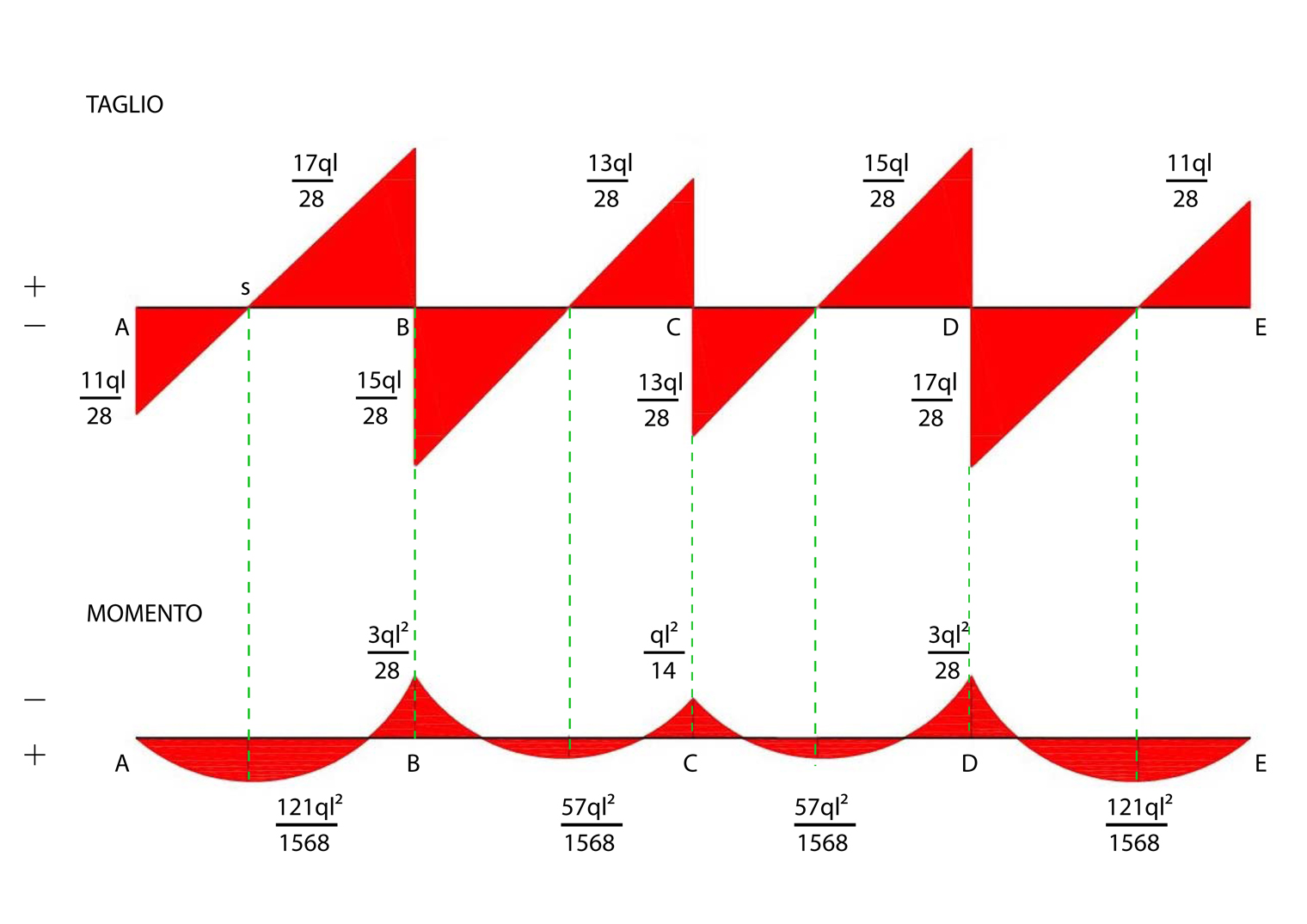
ΣFv(A) = ql/2 – 3ql/28 = 11ql/28

ΣFv(B) = ql + (2) 3ql/28 - ql/14 = 8ql/7

ΣFv(C) = ql - (2) 3ql/28 + (2) ql/14 = 13ql/14

ΣFv(D) =  ΣFv(B) = 8ql/7 (simmetria)

ΣFv(E) = ΣFv(A) = 11ql/28 (simmetria)

Disegno i grafici di Taglio e Momento: