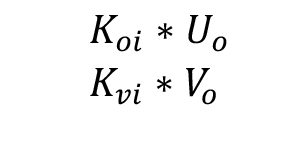Esercitazione: ripartizioni forze sismiche

Prendendo in esame il telaio shear-type abbiamo studiato il concetto di rigidezza tenendo conto che i medesimi elementi strutturali possono avere una doppia funzione, sia come elementi di sostegno verticale della struttura ma anche come elementi di sostegno orizzontale (controvento).

Per rendere efficace un sistema di controventi è necessario considerare l’impalcato infinitamente rigido sul piano orizzontale. I controventi vengono assimilati a molle perché si comportano in modo elastico e hanno una data rigidezza. Sappiamo anche che più sarà la rigidezza e meno sarà lo spostamento. Come possiamo vedere in figura uno dei telai shear-type che andremo poi di seguito ad analizzare sul nostro impalcato.

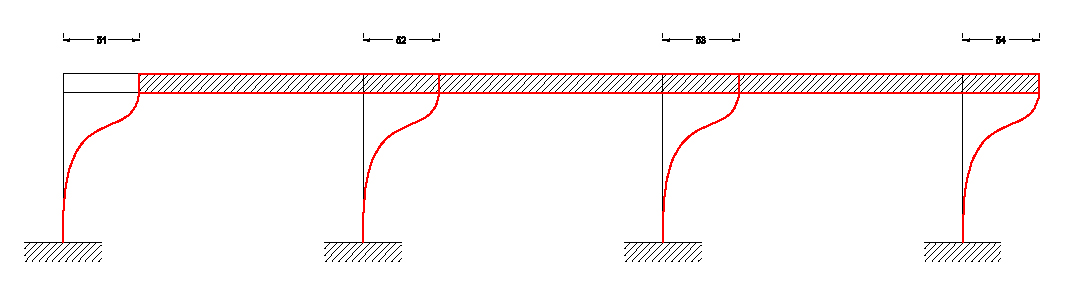
Nel caso più semplici di controventi con eguale rigidezza avremmo una medesima ripartizione della forza agente sull’impalcato così che il corpo traslerà. Mentre se i controventi hanno una diversa rigidezza tra di loro l’impalcato a questo punto non traslerà solamente ma ci sarà anche un effetto di rotazione.

Andiamo ad analizzare un impalcato strutturale. Questo impalcato è individuato da 8 telai piani. 

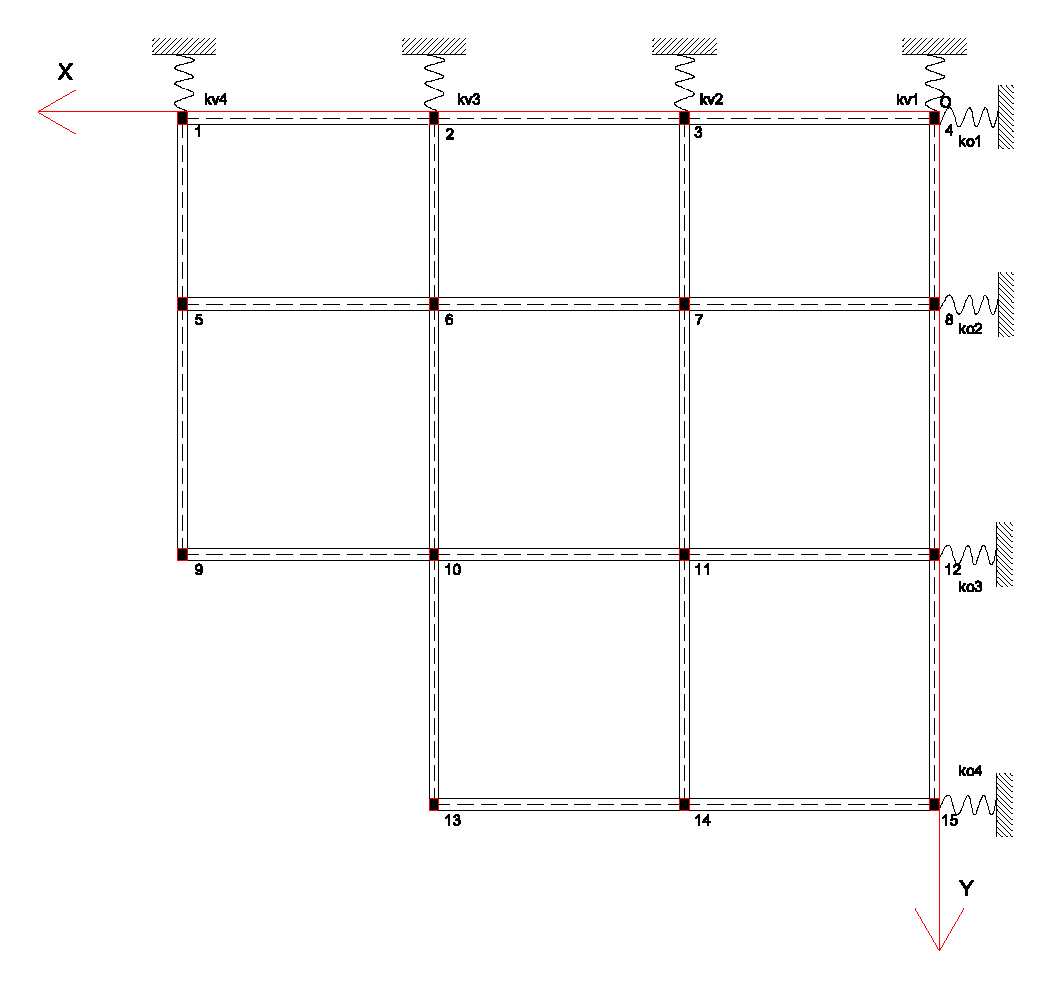
I telai hanno il compito non solo di portare il peso dell’edificio ma anche di controventare la struttura interna resistendo alle forze orizzontali. Il nostro compito sarà quello di:

·         Calcolare le rigidezze traslanti dell’edificio per ogni telaio presente in esso;

·         Calcolare il centro di massa;

·         Calcolare il centro delle rigidezze e la rigidezza torsionale totale;

·         Analizzare i carichi sismici attraverso l’analisi dei carichi permanenti e accidentali;

·         Infine ripartizione delle forze sismiche lungo gli assi X e Y

STEP 1

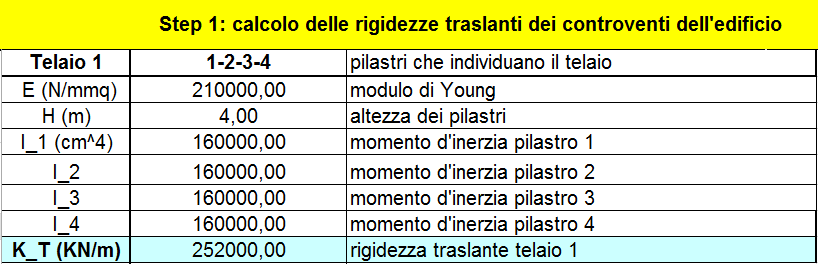
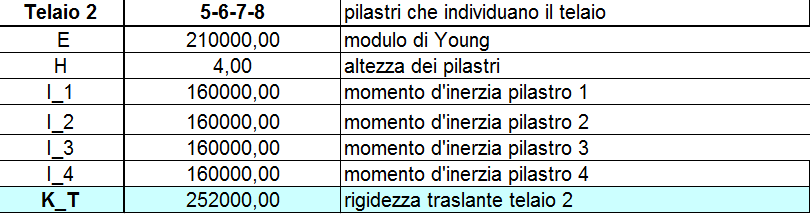
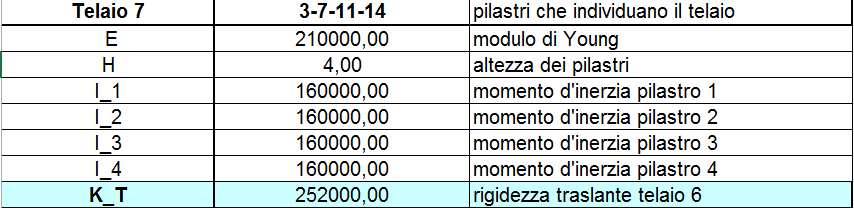
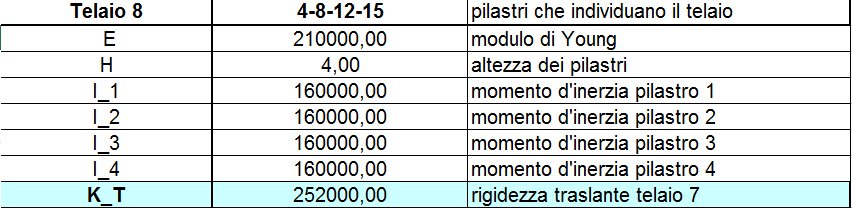
Come abbiamo detto prima il nostro impalcato è composto da 8 telai ed a ognuno viene assegnato un materialo, in questo caso il C.A., una sezione pari a b = 30 cm e h = 40 cm. Calcoliamo come prima cosa la rigidezza traslante per ogni telaio, ovvero la somma delle rigidezze dei singoli pilatri che dipende dal modulo di Young, dal momento d’Inerzia e dall’altezza. L’inerzia è calcolata attraverso l’equazione  .  La rigidezza del telaio è calcolata con la sommatoria di tutte le rigidezze. La rigidezza di un singolo pilastro è uguale a k = 12EI/h³

TELAIO 1

TELAIO 2

TELAIO 3

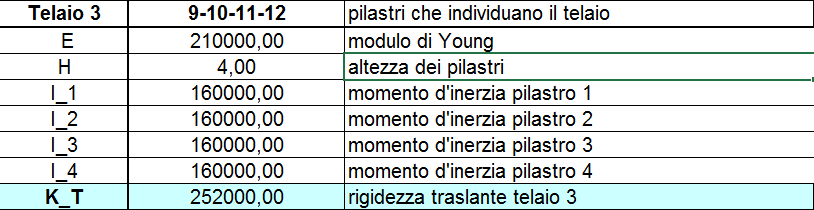
TELAIO 4

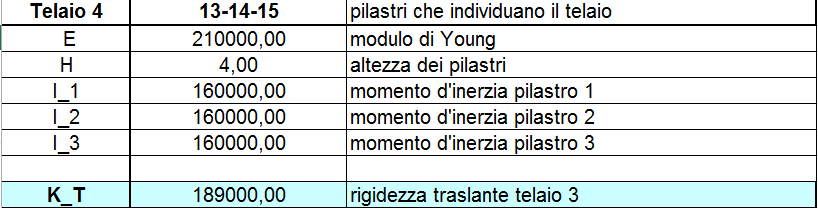
TELAIO 5

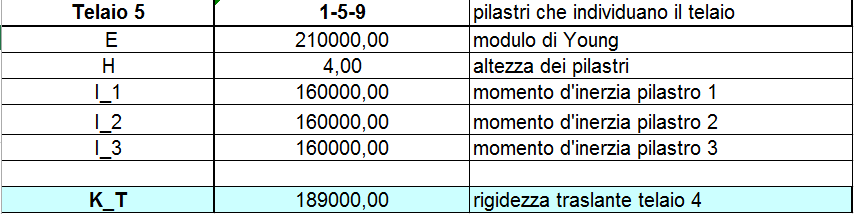
TELAIO 6

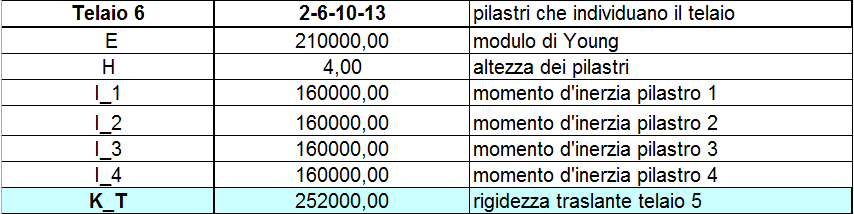
TELAIO 7

TELAIO 8

STEP 2

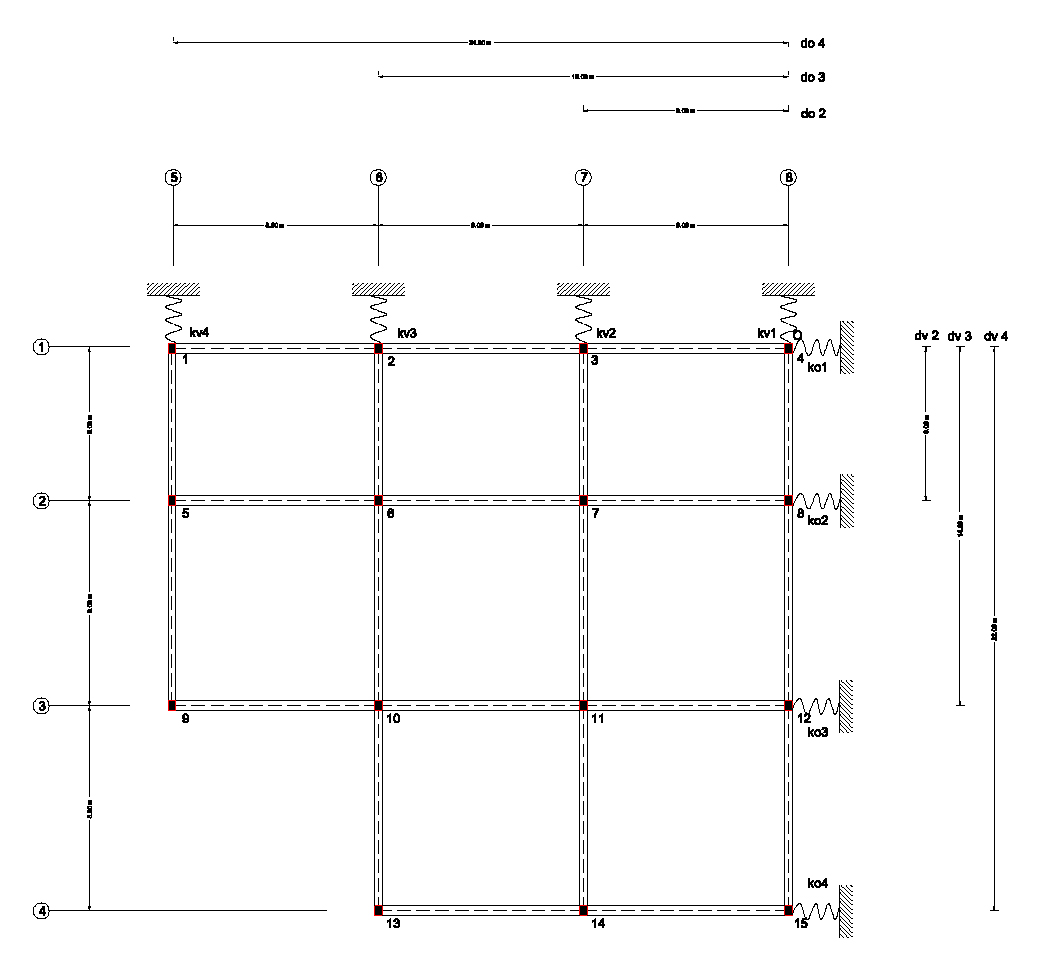
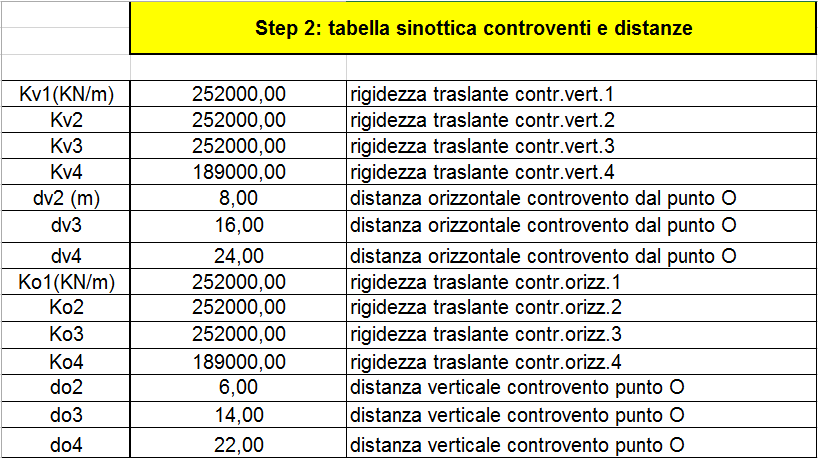
In questa fase raccogliamo in una tabella sinottica le rigidezze traslanti trovate nei controventi e indichiamo la distanza delle molle da un punto O ritenuto origine del sistema di riferimento XY. Questa tabella ci servirà per trovare il centro di massa e delle rigidezze.

STEP 3

Prima di andare avanti vediamo cos’è il centro di massa.

Il centro di massa è il punto di applicazione di tutte le forze, cioè il baricentro di un corpo. Un esempio chiaro del centro di massa è la torre di Pisa che non è mai crollata perché il centro di massa cade all’interno della sua proiezione in pianta.

Per trovare le coordinate prima di tutto dividiamo in due aree rettangolari il nostro impalcato così da trovare il loro baricentro. Misuriamo le coordinate X e Y dei due punti e li andiamo a scrivere nel foglio Excel. Sappiamo che per trovare il baricentro di tutto l’impalcato non dobbiamo far altro che, per il punto X_G, sommare la coordinata X_G1 moltiplicata per l’area 1 (corrisponde a 24m*14m) e la coordinata X_G2 moltiplicata per l’area 2 (corrisponde a 8m*16m) il tutto diviso per l’area totale. Lo stesso procedimento verrà fatto per la coordinata Y così che troviamo le due coordinate del centro di massa dell’impalcato.

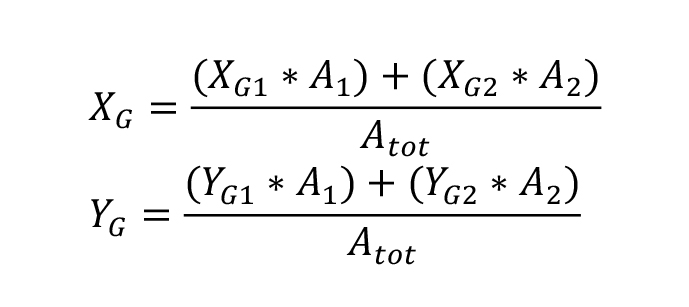
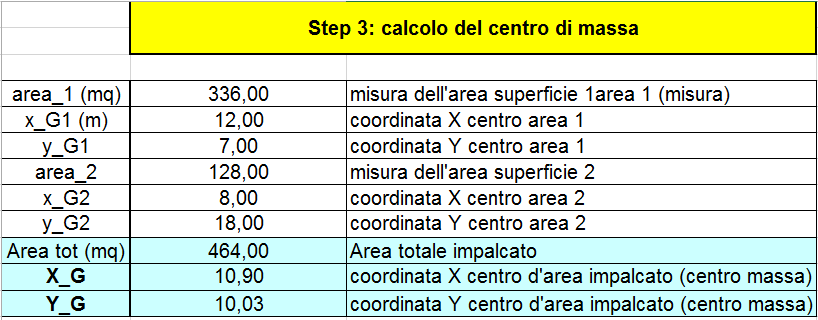
STEP 4

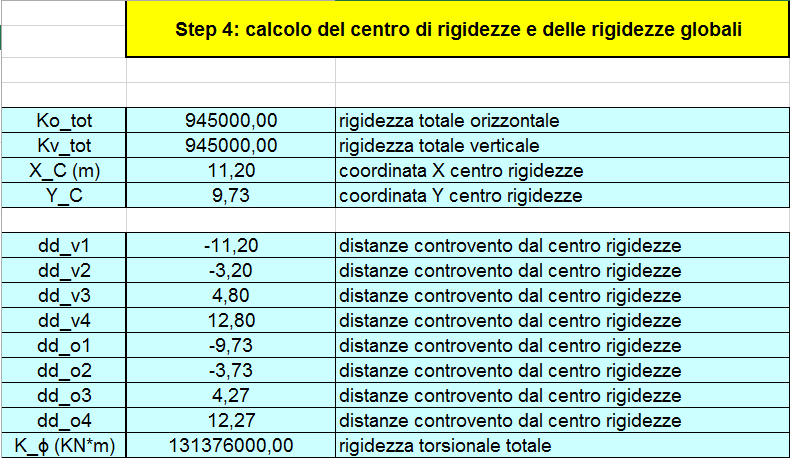
Calcolato il centro di massa ora troviamo il centro delle rigidezze. A differenza del suddetto discorso fatto il centro delle rigidezze è il punto in cui la reazione dell’edificio si concentra.

Per trovare le coordinate del punto X_C sommiamo tutte le rigidezze verticali moltiplicate per le rispettive distanze verticale dall’origine il tutto diviso per la somma delle rigidezze verticali. Lo stesso discorso vale per la coordinata Y_C.

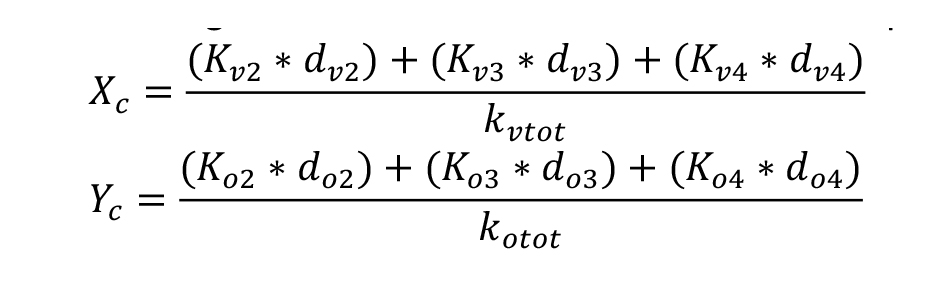
Dopo aver individuato il centro delle rigidezze annotiamo le distanze da esso di ogni controvento (esempio: dd_v2 = d_v2 – X_c)poiché sono necessarie ai fini del calcolo della rigidezza torsionale totale k_φ che si trova con:

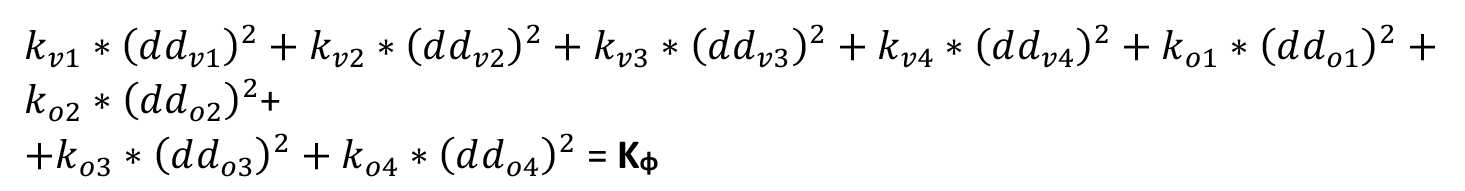
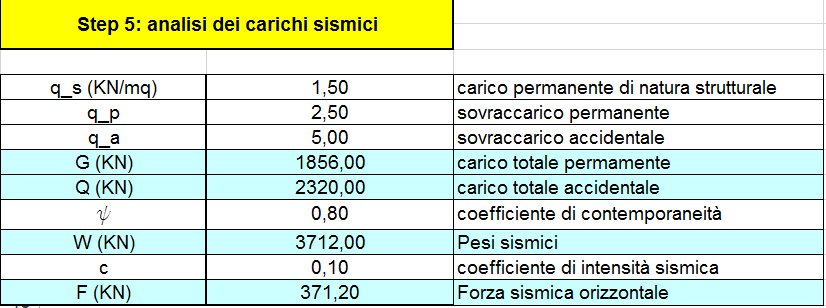
STEP 5

In questo STEP facciamo l’analisi dei carichi sismici agenti sull’implacato. Facciamo un’analisi dei carichi permanenti e sovraccarichi accidentali. I pesi sismici li troviamo con la somma dei carichi totali permanenti e quelli accidentali moltiplicate per il coefficiente di contemporaneità. Mentre la forza sismica orizzontale è calcolata dal prodotto tra pesi sismici totali e il coefficiente di intensità sismica.

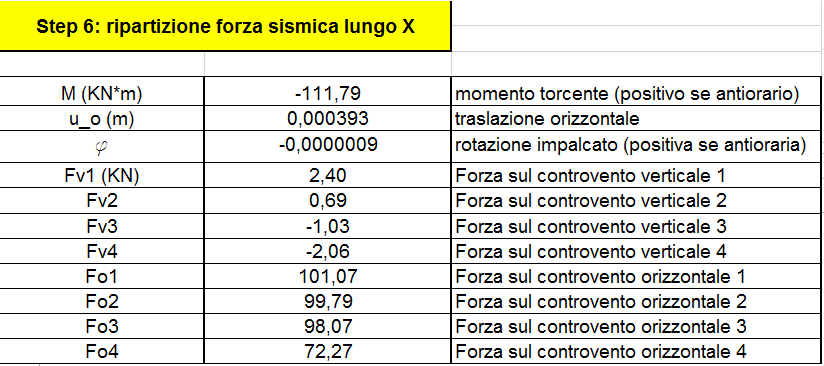
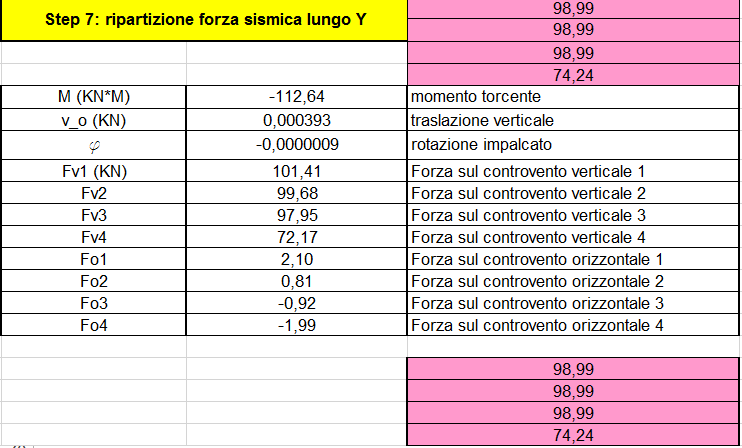
STEP 6-7

Ora ci occupiamo della ripartizione delle forze sismiche sia lungo l’asse X e lungo l’asse Y. Possiamo dire che come prima cosa troviamo il momento torcente che è calcolato con la forza F (forza sismica) e le coordinate del centro di massa e del centro delle rigidezze.

Mx = F * (Yg – Yc)

My = F * (Xg – Xc)

Calcolato il momento, vediamo quant’è la traslazione sia orizzontale e verticale ed si trova con la forza sismica diviso la rigidezza totale.

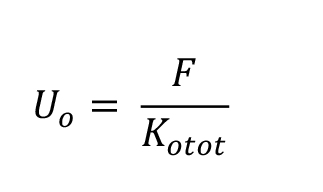
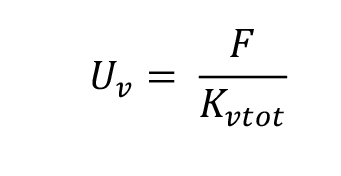
Ci calcoliamo dal foglio excel le forze sui vari controventi attraverso il prodotto di diversi fattori come la rigidezza traslante, la distanza dal controvento al centro delle rigidezze e la rotazione dell’impalcato (per quelli verticali). Mentre per le forze orizzontali è data dal prodotto della rigidezza traslante che moltiplica la somma della traslazione orizzontale e la distanza dal controvento al centro delle rigidezze e quest’ultima moltiplicata per la rotazione traslante.

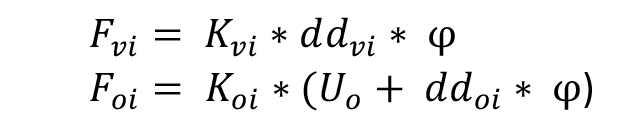
Trovate tutte le forze corrispondente a ogni controvento possiamo trovarci le reazioni vincolare calcolate con :