blog di martina.zaccagnino

Prendendo in esame il telaio shear-type abbiamo studiato il concetto di rigidezza tenendo conto che i medesimi elementi strutturali possono avere una doppia funzione, sia come elementi di sostegno verticale della struttura ma anche come elementi di sostegno orizzontale (controvento).

Per rendere efficace un sistema di controventi è necessario considerare l’impalcato infinitamente rigido sul piano orizzontale. I controventi vengono assimilati a molle perché si comportano in modo elastico e hanno una data rigidezza. Sappiamo anche che più sarà la rigidezza e meno sarà lo spostamento. Come possiamo vedere in figura uno dei telai shear-type che andremo poi di seguito ad analizzare sul nostro impalcato.

Nel caso più semplici di controventi con eguale rigidezza avremmo una medesima ripartizione della forza agente sull’impalcato così che il corpo traslerà. Mentre se i controventi hanno una diversa rigidezza tra di loro l’impalcato a questo punto non traslerà solamente ma ci sarà anche un effetto di rotazione.

Andiamo ad analizzare un impalcato strutturale. Questo impalcato è individuato da 8 telai piani. 

I telai hanno il compito non solo di portare il peso dell’edificio ma anche di controventare la struttura interna resistendo alle forze orizzontali. Il nostro compito sarà quello di:

·         Calcolare le rigidezze traslanti dell’edificio per ogni telaio presente in esso;

·         Calcolare il centro di massa;

·         Calcolare il centro delle rigidezze e la rigidezza torsionale totale;

·         Analizzare i carichi sismici attraverso l’analisi dei carichi permanenti e accidentali;

·         Infine ripartizione delle forze sismiche lungo gli assi X e Y

STEP 1

Come abbiamo detto prima il nostro impalcato è composto da 8 telai ed a ognuno viene assegnato un materialo, in questo caso il C.A., una sezione pari a b = 30 cm e h = 40 cm. Calcoliamo come prima cosa la rigidezza traslante per ogni telaio, ovvero la somma delle rigidezze dei singoli pilatri che dipende dal modulo di Young, dal momento d’Inerzia e dall’altezza. L’inerzia è calcolata attraverso l’equazione  .  La rigidezza del telaio è calcolata con la sommatoria di tutte le rigidezze. La rigidezza di un singolo pilastro è uguale a k = 12EI/h³

TELAIO 1

TELAIO 2

TELAIO 3

TELAIO 4

TELAIO 5

TELAIO 6

TELAIO 7

TELAIO 8

STEP 2

In questa fase raccogliamo in una tabella sinottica le rigidezze traslanti trovate nei controventi e indichiamo la distanza delle molle da un punto O ritenuto origine del sistema di riferimento XY. Questa tabella ci servirà per trovare il centro di massa e delle rigidezze.

STEP 3

Prima di andare avanti vediamo cos’è il centro di massa.

Il centro di massa è il punto di applicazione di tutte le forze, cioè il baricentro di un corpo. Un esempio chiaro del centro di massa è la torre di Pisa che non è mai crollata perché il centro di massa cade all’interno della sua proiezione in pianta.

Per trovare le coordinate prima di tutto dividiamo in due aree rettangolari il nostro impalcato così da trovare il loro baricentro. Misuriamo le coordinate X e Y dei due punti e li andiamo a scrivere nel foglio Excel. Sappiamo che per trovare il baricentro di tutto l’impalcato non dobbiamo far altro che, per il punto X_G, sommare la coordinata X_G1 moltiplicata per l’area 1 (corrisponde a 24m*14m) e la coordinata X_G2 moltiplicata per l’area 2 (corrisponde a 8m*16m) il tutto diviso per l’area totale. Lo stesso procedimento verrà fatto per la coordinata Y così che troviamo le due coordinate del centro di massa dell’impalcato.

STEP 4

Calcolato il centro di massa ora troviamo il centro delle rigidezze. A differenza del suddetto discorso fatto il centro delle rigidezze è il punto in cui la reazione dell’edificio si concentra.

Per trovare le coordinate del punto X_C sommiamo tutte le rigidezze verticali moltiplicate per le rispettive distanze verticale dall’origine il tutto diviso per la somma delle rigidezze verticali. Lo stesso discorso vale per la coordinata Y_C.

Dopo aver individuato il centro delle rigidezze annotiamo le distanze da esso di ogni controvento (esempio: dd_v2 = d_v2 – X_c)poiché sono necessarie ai fini del calcolo della rigidezza torsionale totale k_φ che si trova con:

STEP 5

In questo STEP facciamo l’analisi dei carichi sismici agenti sull’implacato. Facciamo un’analisi dei carichi permanenti e sovraccarichi accidentali. I pesi sismici li troviamo con la somma dei carichi totali permanenti e quelli accidentali moltiplicate per il coefficiente di contemporaneità. Mentre la forza sismica orizzontale è calcolata dal prodotto tra pesi sismici totali e il coefficiente di intensità sismica.

STEP 6-7

Ora ci occupiamo della ripartizione delle forze sismiche sia lungo l’asse X e lungo l’asse Y. Possiamo dire che come prima cosa troviamo il momento torcente che è calcolato con la forza F (forza sismica) e le coordinate del centro di massa e del centro delle rigidezze.

Mx = F * (Yg – Yc)

My = F * (Xg – Xc)

Calcolato il momento, vediamo quant’è la traslazione sia orizzontale e verticale ed si trova con la forza sismica diviso la rigidezza totale.

Ci calcoliamo dal foglio excel le forze sui vari controventi attraverso il prodotto di diversi fattori come la rigidezza traslante, la distanza dal controvento al centro delle rigidezze e la rotazione dell’impalcato (per quelli verticali). Mentre per le forze orizzontali è data dal prodotto della rigidezza traslante che moltiplica la somma della traslazione orizzontale e la distanza dal controvento al centro delle rigidezze e quest’ultima moltiplicata per la rotazione traslante.

Trovate tutte le forze corrispondente a ogni controvento possiamo trovarci le reazioni vincolare calcolate con :

Metodo delle forze

Struttura tre volte iperstatica la studiamo come un corpo isostatico svincolando in B, in C e in D assegnando due momenti incogniti X₁ e X₂ in D sarà sempre X₁ poiche la trave è simmetrica, così da interrompere la trave e creare 4 pezzi di trave isostatica

Per risolvere il sistema parto dai tre momenti e come prima cosa imponiamo la congruenza e scriviamo che le nostre tre equazioni di congruenza siano uguali a zero. 

Nei punti in cui abbiamo inserito le congruenze avremo due equazioni in cui una guarda a destra e una a sinistra. Le eguagliamo e mettendole a sistema andremo a trovare le nostre incognite X₁ e X₂.

Disegno le reazioni vincolari trovate dalla congruenza assegnata e le reazioni date dal carico distribuito

Faccio la sovrapposizione degli effetti sommando i due schemi per trovare le reazioni vincolare della struttura iperstatica. nel primo diagramma ci sono le congruenze.

Nel secondo vediamo le reazioni dovute al carico distribuito

E questa è la sovrapposizione dei due schemi delle reazioni vincolari

Ora possiamo calcolarci i diagrammi delle sollecitazioni di Taglio e del Momento

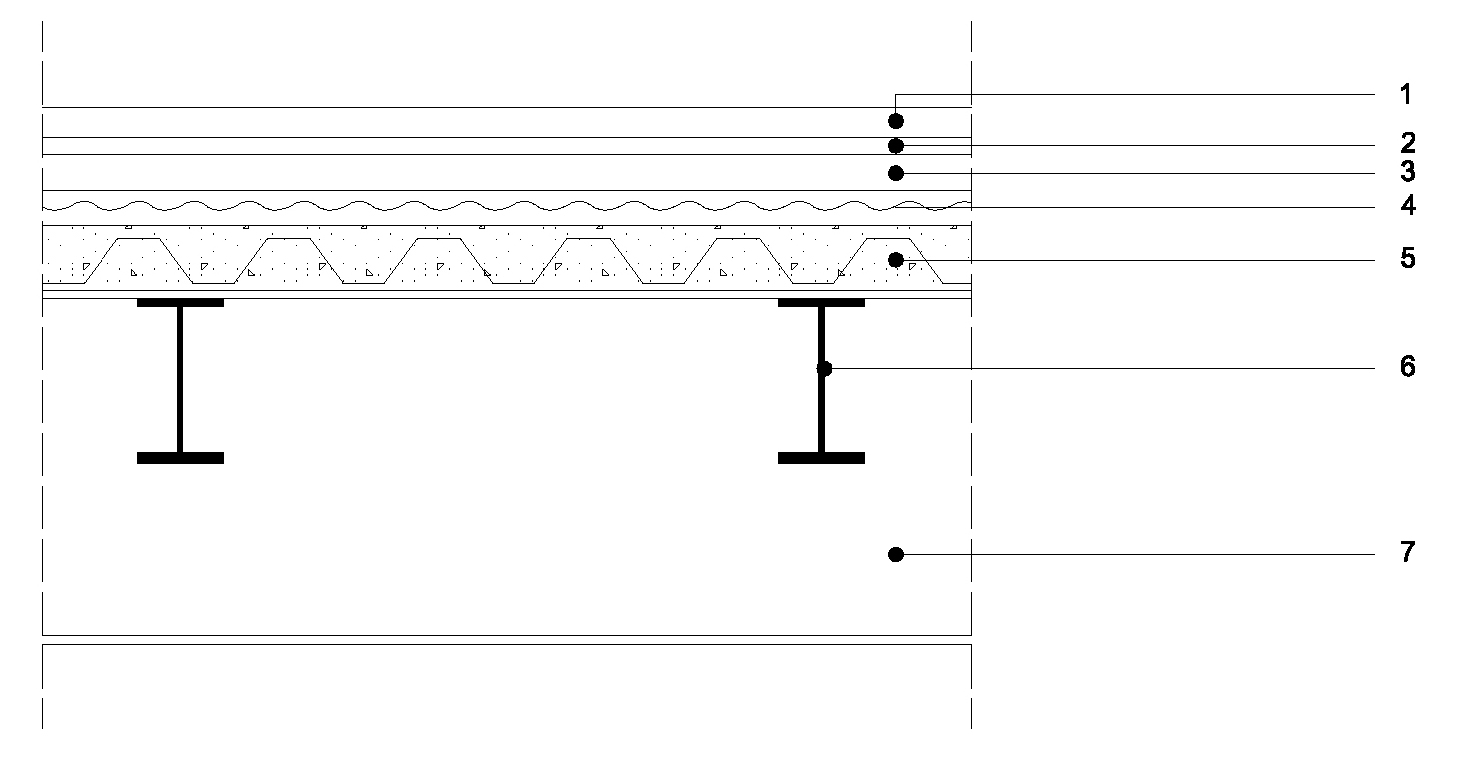
STRATI DELLA SEZIONE

1_ pavimento in parquet di quercia_ 8KN/mc (sp. 0,025 m)

2_allettamento_ 2KN/mc (sp. 0,015m)

3_massetto_ 20KN/mc (sp. 0,03m)

4_isolante termico_ 3KN/mc (sp. 0,03m)

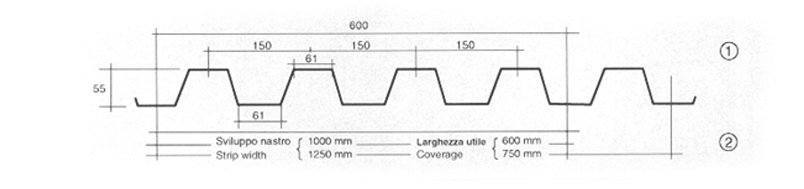
5_lamiera grecata EGB 210con soletta in cls_ 2,50KN/mq

6_trave secondaria

7_trave principale

DIMENSIONAMENTO DELLA TRAVE SECONDARIA

Analisi dei carichi:

            Carichi strutturali q_s:

                        _lamiera grecata EGB 210 con soletta in cls = 2,50KN/mq STRATI DELLA SEZIONE

Carichi permanenti q_p:

                        _ pavimento in parquet di quercia = 8KN/mc * 0,025 m = 0,2 KN/mq

            _allettamento = 2KN/mc * 0,015m = 0,03 KN/mq

            _massetto = 20KN/mc * 0,03m = 0,6 KN/mq

            _isolante termico = 3KN/mc * 0,03m = 0,09 KN/mq

            _tramezzi e impianti = 1,5 KN/mq

Carichi accidentale q_a:

                        _edificio adibito a civile abitazione = 2,00 KN/mq

Facciamo la somma dei carichi totali applicando ai carichi i coefficienti di sicurezza sfavorevoli:

Q_tot= (q_s * γ_s)+ (q_p * γ_p) + (q_a * γ_a)= (2,50KN/mq * 1,3) + (2,42 KN/mq * 1,5) + (2,00KN/mq * 1,5) = 9,88KN/mq

Avremmo :

• q_s = 3,25 KN/mq
• q_p = 3,63 KN/mq
• q_a = 3,00 KN/mq

Otteniamo un carico ripartito lineare moltiplicando il Q_tot per l’interasse così da ottenere Q_tot/lineare = 9,88 KN/m.

Con l'entrata in vigore del D.M. del 14 gennaio 2008 gli acciai da carpenteria devono appartenere al grado da S 235 a S 460. Scelgo per questa sezione la classe di resistenza Fe 360/S235.

Fatto questo andiamo ad inserire i valori trovati nel foglio exel

Inserito l’interasse e i carichi trovati e il carico lineare scriviamo il momento che è = (ql²)/8. Il momento trovato è pari a 44,46 KN*m. Scriviamo la tensione di snervamento caratteristica scelta e troviamo così W_x.

Il profilo corrispondente al valore di 217,57 cm³ è la sezione IPE 220 che ha un valore di W_x pari a 252,0 cm³ . Non potevamo prendere la sezione IPE 200 poiché il valore di W_x è più piccolo.

PRIMA VERIFICA

Peso della trave = 26,2 Kg/m (valore tabellato) calcolato al metro lineare àcorrisponde a 0,26 KN/mq

Aggiungiamo ai carici strutturali il peso proprio della trave e lo andiamo a inserire nel foglio exel. Troviamo che il valore del q_s = 3,51 KN/mq

Possiamo vedere che la trave con sezione IPE 220 è verificata poiché avendo inserito il peso proprio della trave il W_x è rimasto inferiore a quello della sezione.

DIMENSIONAMENTO DELLA TRAVE PRINCIPALE

Analisi dei carichi:

            Carichi strutturali q_s:

                        _lamiera grecata EGB 210 con soletta in cls = 2,50KN/mq

                        _trave secondaria = 0,22 KN/mq

            Carichi permanenti q_p:

                        _ pavimento in parquet di quercia = 8KN/mc * 0,025 m = 0,2 KN/mq

            _allettamento = 2KN/mc * 0,015m = 0,03 KN/mq

            _massetto = 20KN/mc * 0,03m = 0,6 KN/mq

            _isolante termico = 3KN/mc * 0,03m = 0,09 KN/mq

            _tramezzi e impianti = 1,5 KN/mq

Carichi accidentale q_a:

                        _edificio adibito a civile abitazione = 2,00 KN/mq

Facciamo la somma dei carichi totali applicando ai carichi i coefficienti di sicurezza sfavorevoli:

Q_tot= (q_s * γ_s)+ (q_p * γ_p) + (q_a * γ_a)= (2,72KN/mq * 1,3) + (2,42 KN/mq * 1,5) + (2,00KN/mq * 1,5) =10,17 KN/mq

Otteniamo un carico ripartito lineare moltiplicando il Q_tot per l’interasse così da ottenere Q_tot/lineare = 61,02 KN/m.

Anche per questa trave scegliamo il fattore di snervamento pari a S235 N/mm² e li andiamo ad inserire nel foglio exel.

Inserito l’interasse e i carichi trovati e il carico lineare scriviamo il momento che è = (ql²)/8. Il momento trovato è pari a 488,16 KN*m. Scriviamo la tensione di snervamento caratteristica e troviamo così W_x.

Il profilo corrispondente al valore di 2388,87 cm³ è la sezione IPE 550 che ha un valore di W_x pari a 2668,0 cm³ .

PRIMA VERIFICA

Peso della trave = 106,0 Kg/m (valore tabellato) calcolato al metro quadrato àcorrisponde a 1,04 KN/mq

Aggiungiamo ai carici strutturali il peso proprio della trave e lo andiamo a inserire nel foglio exel. Troviamo che il valore del q_s = 4,55 KN/mq

Possiamo vedere che la trave con sezione IPE 550 non è verificata poiché la sezione ha un valore minore di W_x rispetto a quello trovato. Scegliamo così la sezione successiva di IPE 600 con valore di W_x pari a 3070,0 cm³ .

SECONDA VERIFICA

Peso della trave = 122,0 Kg/m àcorrisponde a 1,19 KN/mq

Aggiungiamo ai carici strutturali il peso proprio della trave e lo andiamo a inserire nel foglio exel. Troviamo che il valore del q_s = 4,7 KN/mq

Possiamo vedere che la trave con sezione IPE 600 è verificata poiché la sezione ha un valore minore di W_x rispetto a quello tabellato.

Abbiamo trovato le sezioni delle due travi per una luce di 8 m.