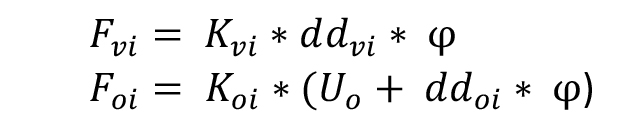Esercitazione RIPARTIZIONE DELLE FORZE SISMICHE

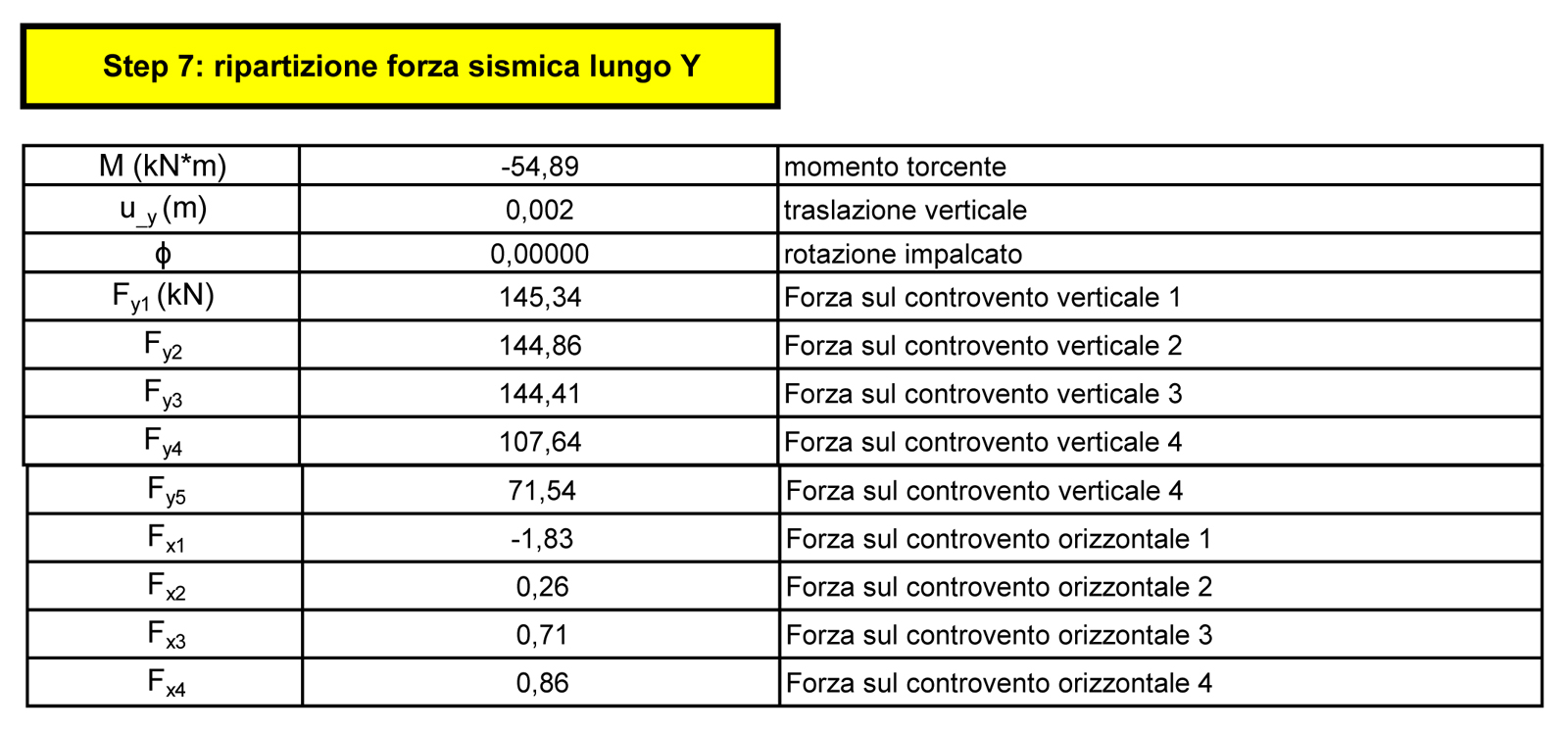
Inviato da giustino.cacciotti il Sab, 15/06/2013 - 21:14

Se consideriamo gli impalcati come corpi rigidi sul proprio piano, gli spostamenti che essi potranno compiere saranno: traslazione verticale Uv (m), orizzontale Uo (m) e rotazione φ.

Per esempio la forza orizzontale (forza sismica o la forza del vento) tende a spostarli, ma i controventi contrastano questa azione grazie alla loro elasticità.

Il controvento nell’impalcato piano può essere definito come un appoggio cedevole elasticamente infatti essi sono come molle con una data rigidezza K (kN/m). In un impalcato queste rigidezze possono essere differenti e causare una rotazione.

1. Il nostro impalcato è composto da 8 telai ed a ognuno viene assegnato un materiale, in questo caso il C.A., una sezione dei pilastri pari a
 b = 40 cm e h = 50 cm.
STEP 1. Il nostro impalcato è composto da 8 telai ed a ognuno viene assegnato un materiale, in questo caso il C.A. e una sezione dei pilastri pari a
 
 b = 40 cm e h = 50 cm
 
Per prima cosa calcoliamo la rigidezza traslante per ogni telaio KT (kN/m) la somma delle rigidezze dei singoli pilatri dove:
E (N/mm2) = modulo di Young (21000 per il calcestruzzo)
I (cm4) = momento di inerzia di ogni pilastro del telaio  I = bh3/12       
h = altezza dei pilastri dell'impalcato
Per prima cosa calcoliamo la rigidezza traslante per ogni telaio KT (kN/m) la somma delle rigidezze dei singoli pilatri dove la rigidezza di un singolo pilastro è uguale a k = 12EI/h3    
 
E (N/mm2) = modulo di Young (21000 per il calcestruzzo)
I (cm4) = momento di inerzia di ogni pilastro del telaio  I = bh3/12       
h = altezza dei pilastri dell'impalcato
E (N/mm2) = modulo di Young (21000 per il calcestruzzo)
I (cm4) = momento di inerzia di ogni pilastro del telaio  I = bh3/12       
E (N/mm2) = modulo di Young (21000 per il calcestruzzo)
I (cm4) = momento di inerzia di ogni pilastro del telaio  I = bh3/12       
E (N/mm2) = modulo di Young (21000 per il calcestruzzo)
I (cm4) = momento di inerzia di ogni pilastro del telaio  I = bh3/12
h (m)= altezza dei pilastri dell'impalcato
 
   

 

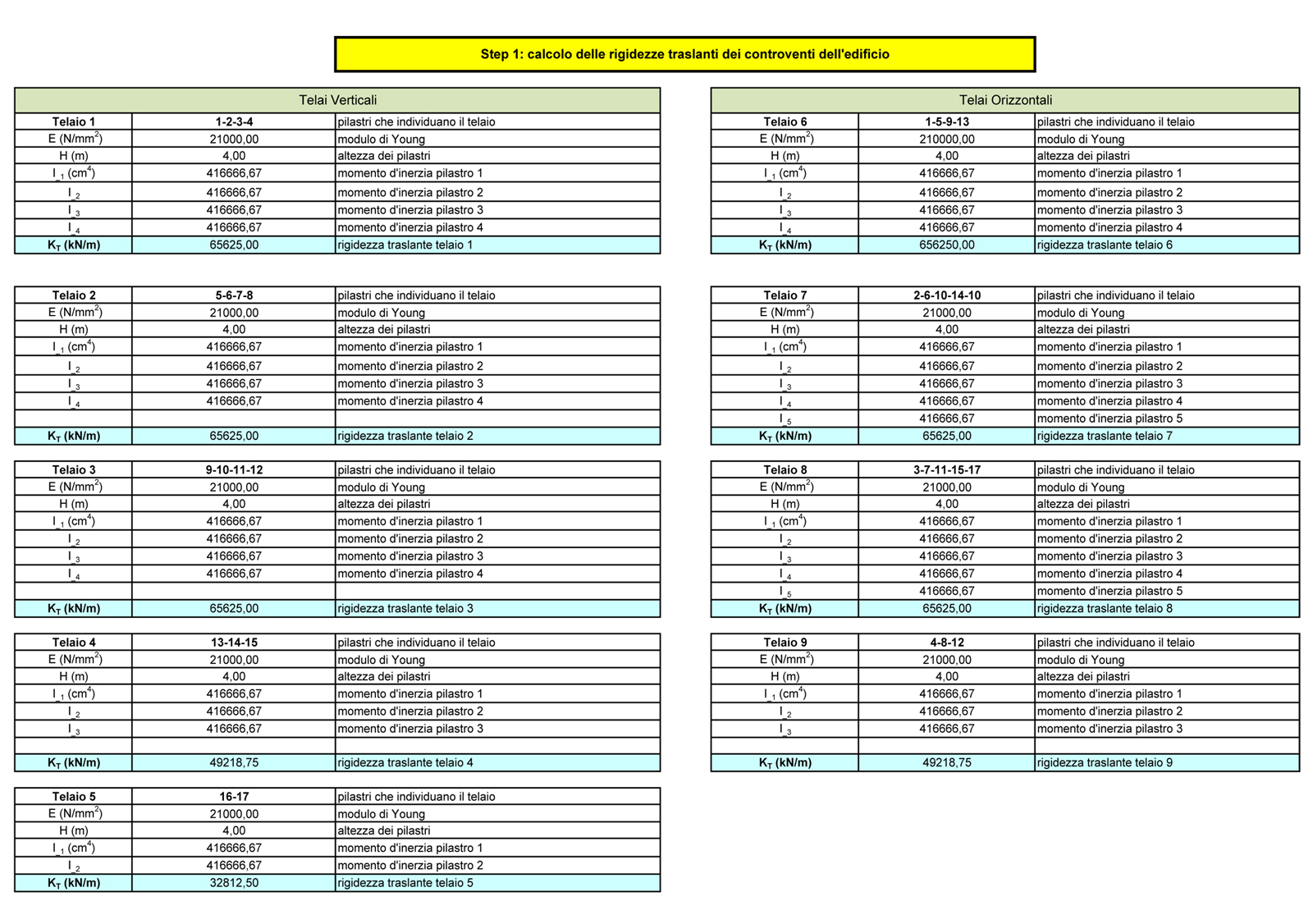
STEP 2.   In questa tabella raccogliamo le rigidezze traslanti verticali Kv (kN/m) e orizzontali Ko (kN/m) dei controventi e la loro distanza dal punto zero (0) all'origine.

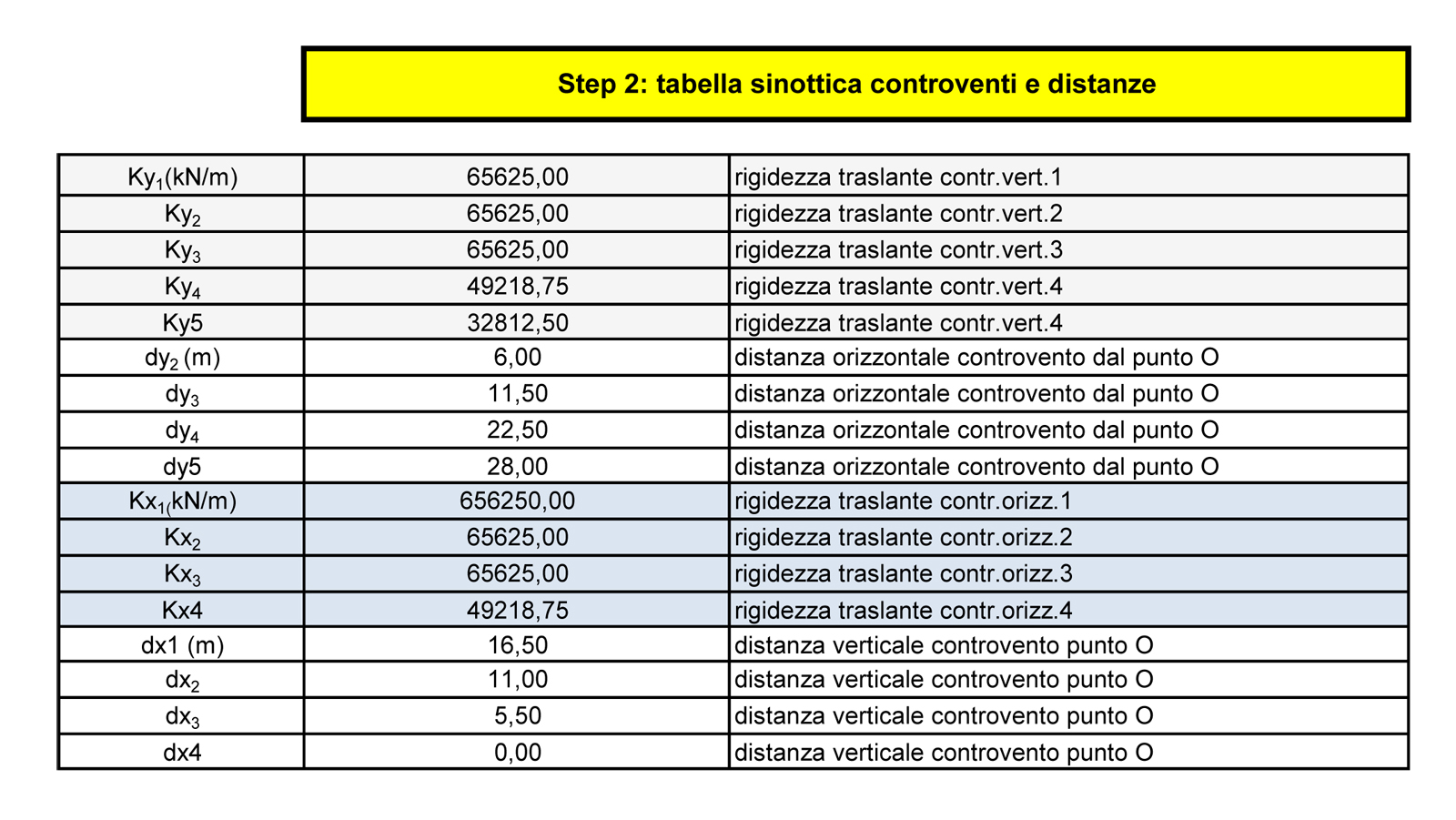
STEP 3.  Una volta stabilite le rigidezze dei telai e le rispettive distanze dallo zero, troviamo  le coordinate del centro delle masse G (m). Esso può essere definito come il baricentro di un corpo, il punto in cui vanno a concentrarsi tutte le forze. 

Per calcolarmi G, il centro delle masse  divido la struttura in quattro parti e definisco le aree di ciascuna inoltre ho bisogno dei seguenti dati:

  • Area di ciascuna parte
  • Per ogni parte le coordinate (x,y) proprio centro nell’area specifica
  • Area totale impalcato

 

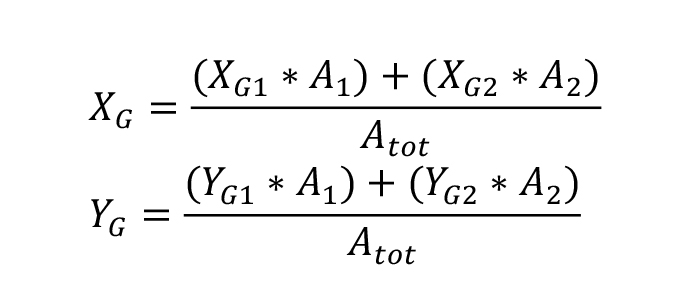
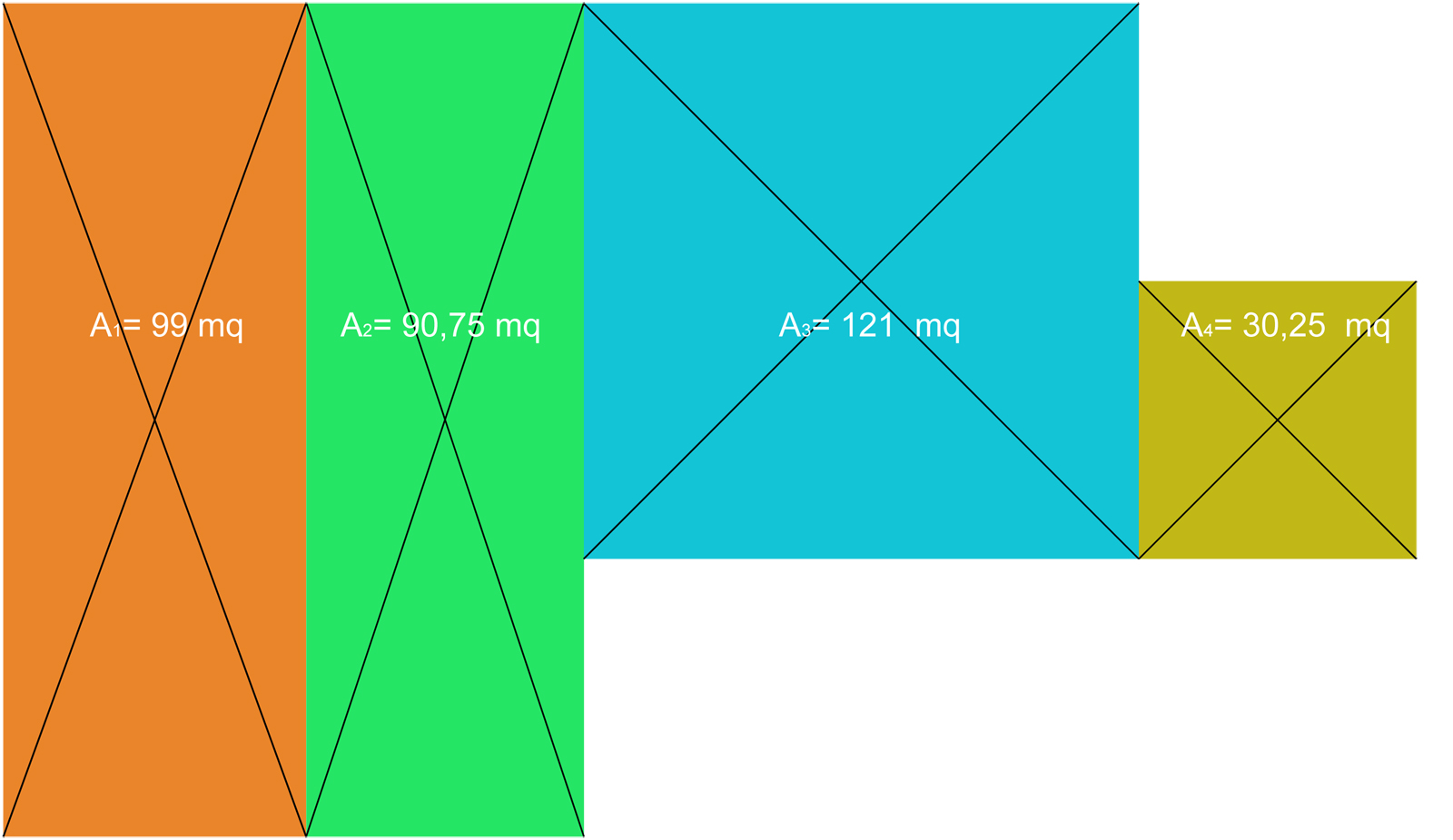
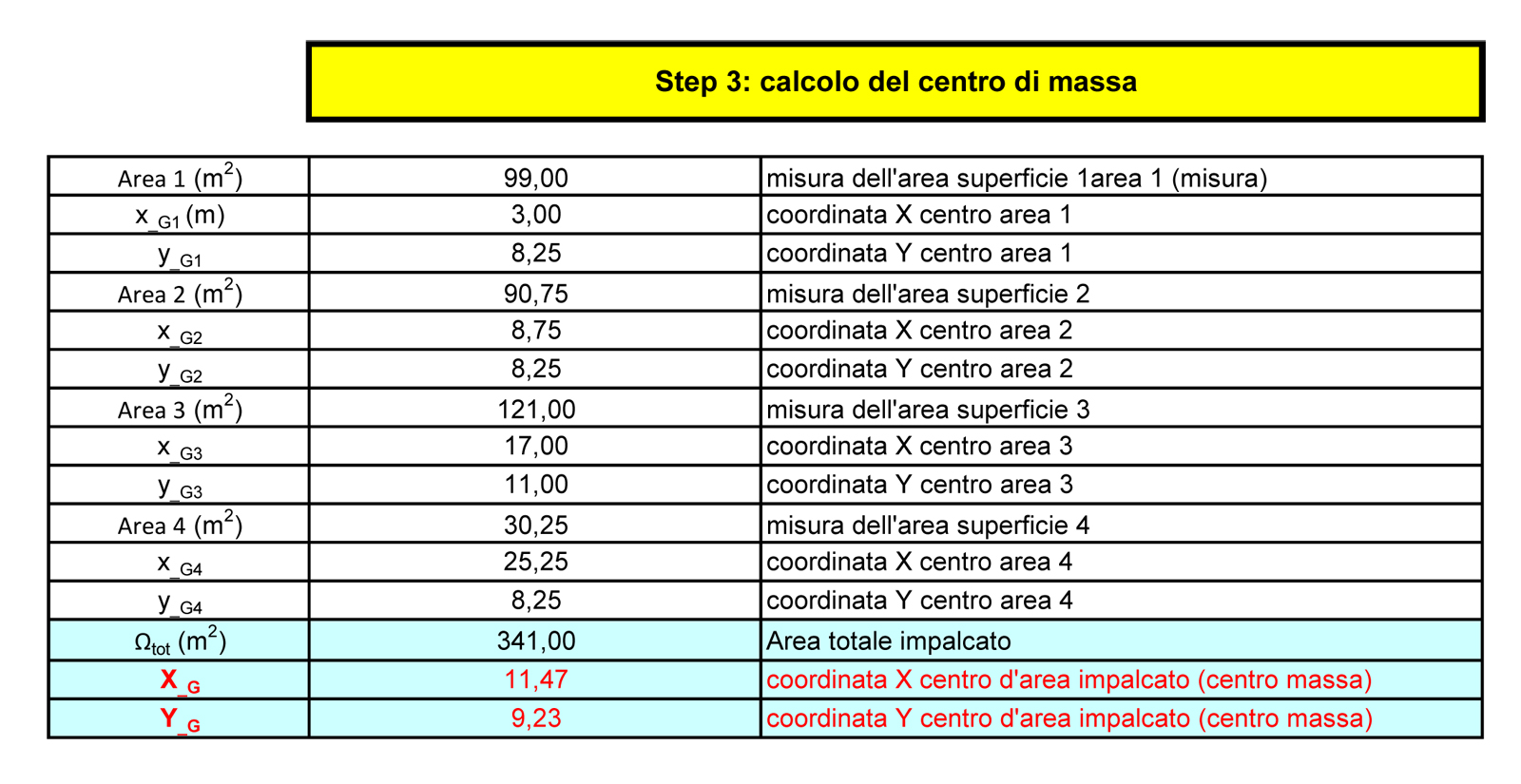
Le coordinate (XG,YG) del centro delle masse dell’impalcato sono: (11,47; 9,23)

 

STEP 4. Calcolato il centro delle masse ora cerchiamo il centro delle rigidezze C (m) che è determinato dal punto in cui si concentra la reazione dell’edificio.

Per trovare le coordinate del punto Xc e Yc ho bisogno dei seguenti dati:

  • la rigidezza verticale di ogni telaio
  • la distanza di ognuno rispetto al punto zero
  • la rigidezza totale di tutti i telai (verticale perX e orizzontale per Y)

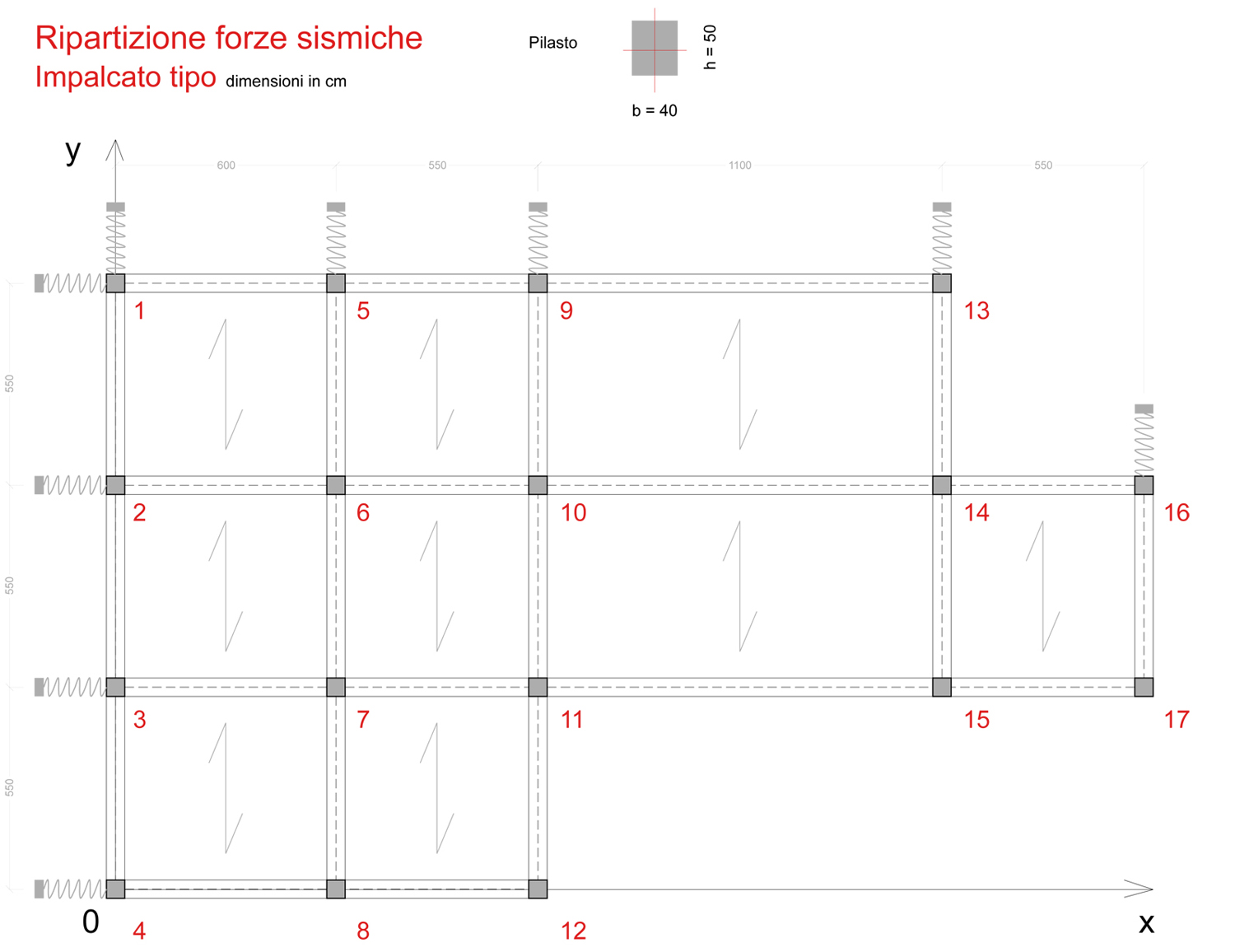
La formula segue:

La variabile dd indica la distanza dei controventi dal centro delle rigidezze C. 

Il centro delle rigidezze è posto al controvento più rigido.

La presenza di segno negativo o positivo di dd sta ad indicare una rotazione rispetto a C oraria o antioraria dei telai.

Inoltre dd è necessaria ai fini di calcolo della rigidezza torsionale totale kφ

 

 

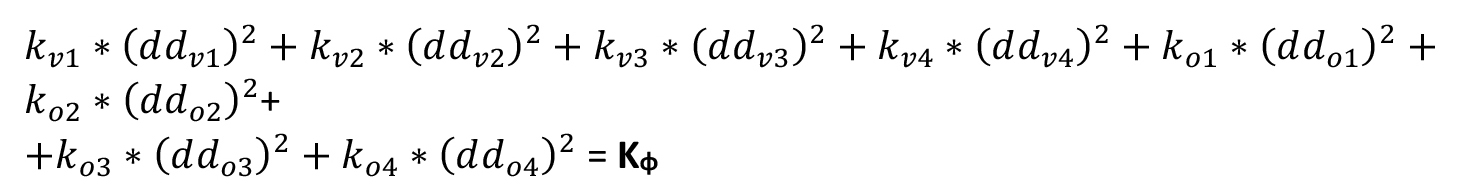
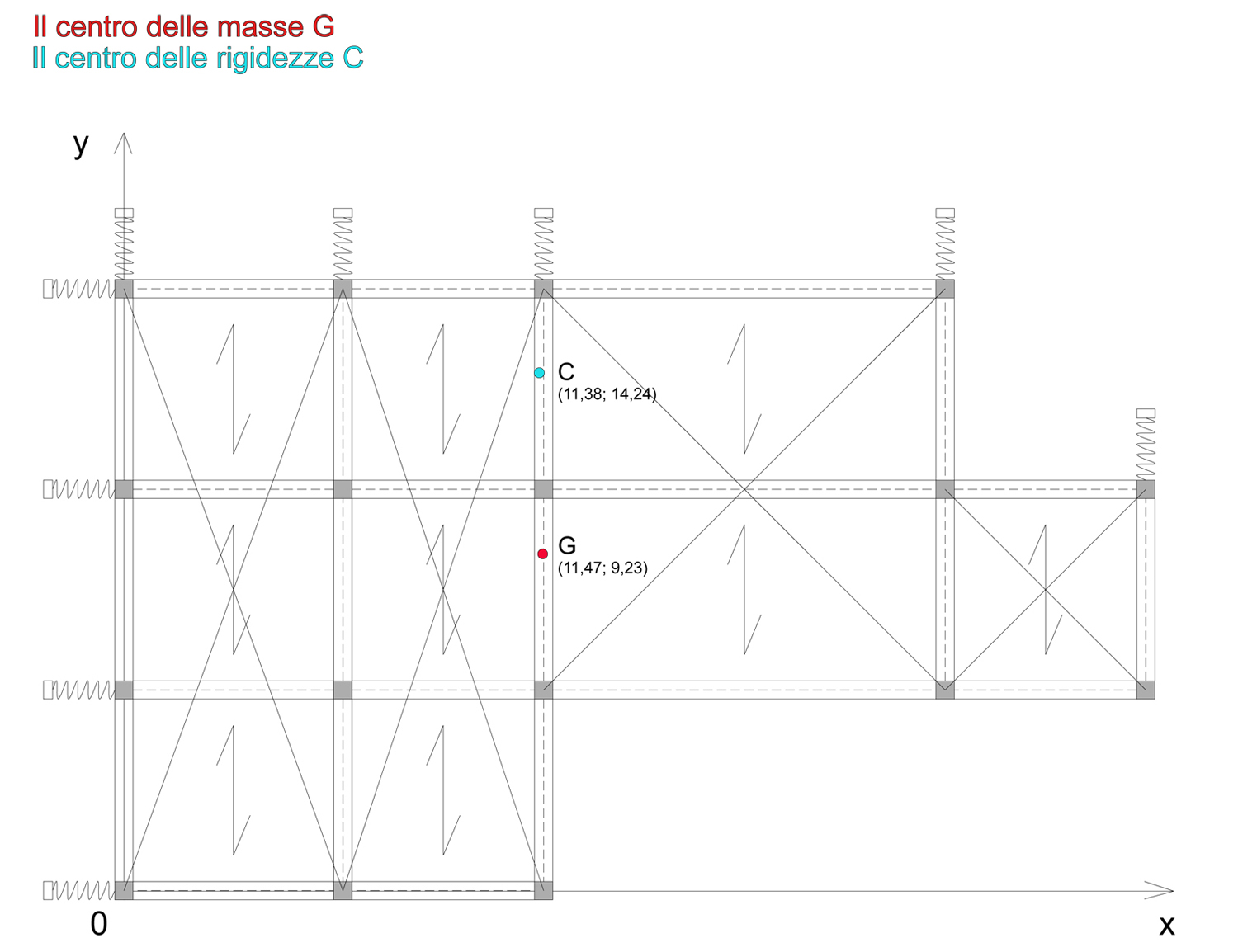
Le coordinate (XC,YC) del centro delle masse dell’impalcato sono: (11,38; 14,24)

 

 

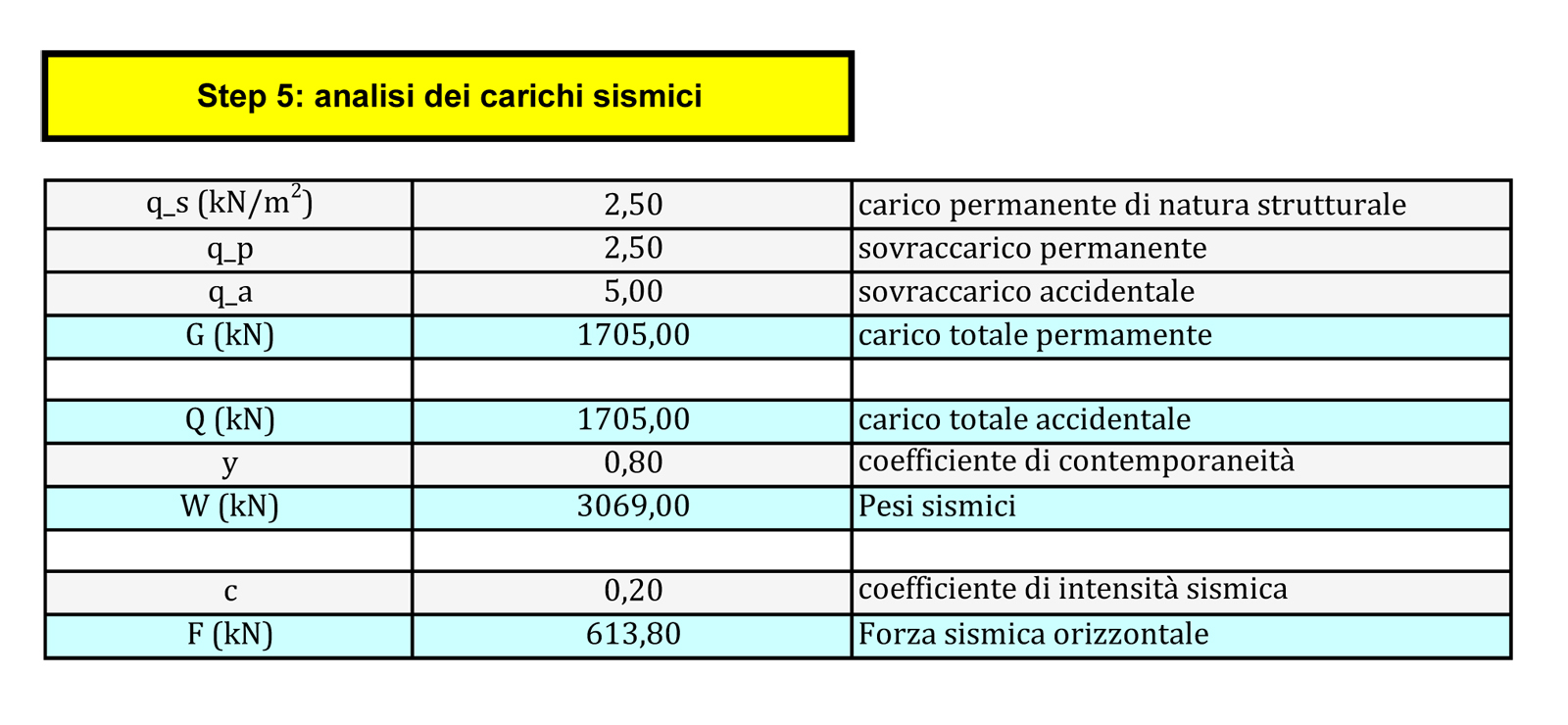
STEP 5. Analisi dei carichi sismici. Per trovare  la forza sismica calcoliamo, il peso dell'impalcato, dopo aver definito i carichi strutturali, accidentali e permanenti che agiscono sulla struttura per il coeficente di contemporaneità (y) dato dalla normativa, che diminuisce il carico accidentale.

La forza sismica agisce dove c’è più massa. Più un elemento è pesante più esso è vulnerabile alla forza sismica.

La forza sismica orizzontale F (kN) è data dal prodotto dei pesi sismici totali per il coefficente di intensità sismica.

G (kN) = carico totale permanente = (qs + qp) Atot

Q (kN) = carico totale accidentale = qa Atot

W (kN) = peso sismico

(y) =  coefficente di contemporaneità

(c) = coefficente d'intensità sismica

quindi

 F (kN) = W*(c) dove W (kN) = G + Q*(y)

STEP 6: ripartizione forza sismica lungo X. Non è possibile prevedere quando e su che asse la forza sismica agirà. Essa viene calcolata con la Forza F (kN) per (Yc-XG), il braccio della forza cioè la distanza tra la coordinata del centro delle rigidezze e il centro di massa.

Mx = F * (Yc – YG)

My = F * (Xc – XG)

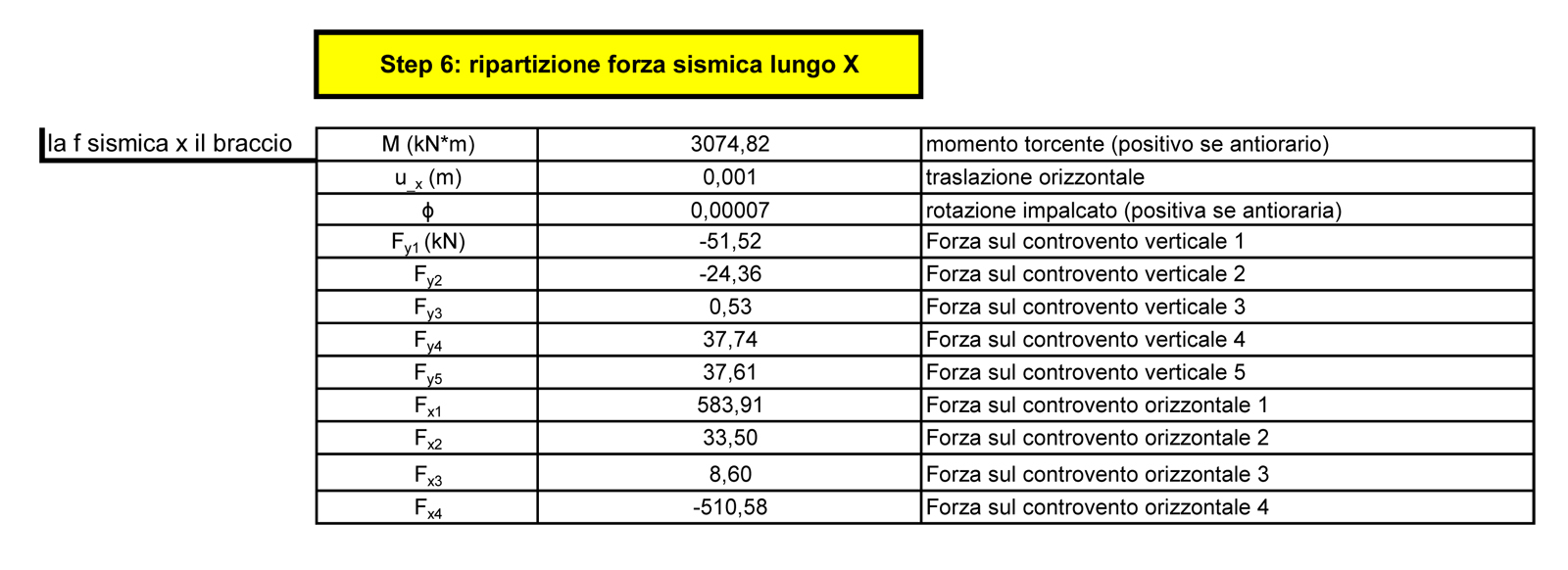
Una volta calcolato il momento torcente, troviamo la traslazione verticale Uv (m), orizzontale Uo (m) e la rotazione dell'impalcato φ = M (momento torcente) / Kϕ (rigidezza torsionale totale)

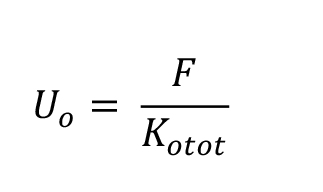
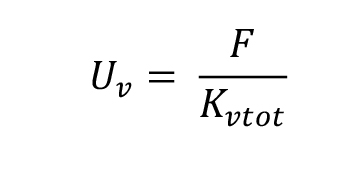
è possibile individuare (utilizzando excel) come la forza sismica si ripartisce su ogni controvento in base alla sua rispettiva rigidezza.

Avremo bisogno dei seguenti dati:

Per i controventi Verticali:

  • la rigidezza traslante controvento Kvi (kN/m)
  • la distanza controvento dal centro rigidezze ddvi (m)
  • la rotazione dell’impalcato φ

Per i controventi Orizzontali:

  • rigidezza traslante Koi (kN/m)
  • la somma della traslazione orizzontale Uo (m)
  • la distanza dal controvento al centro delle rigidezze ddoi (m)e quest’ultima moltiplicata per la rotazione traslante φ