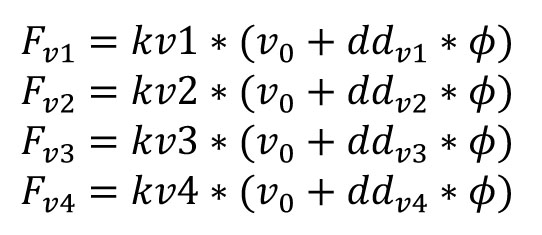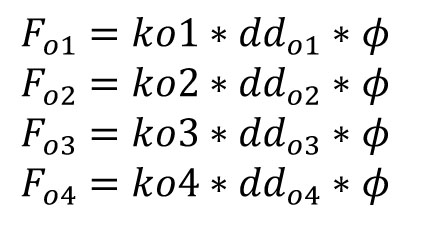ripartizione di forze sismiche

Ripartizione di forze sismiche

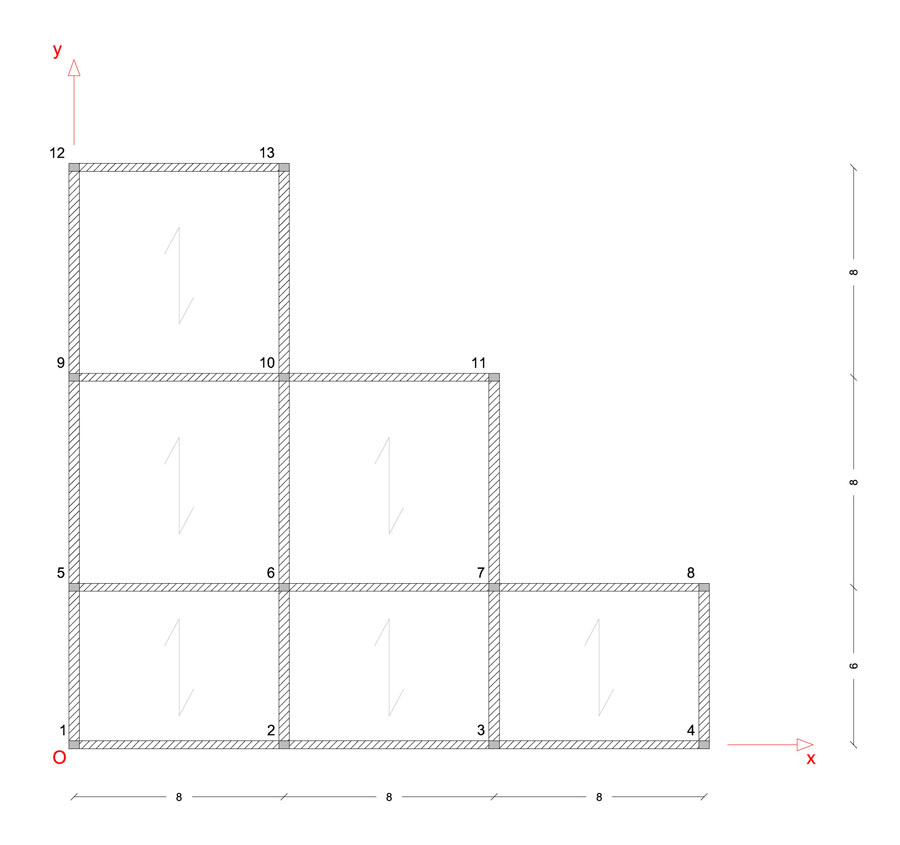
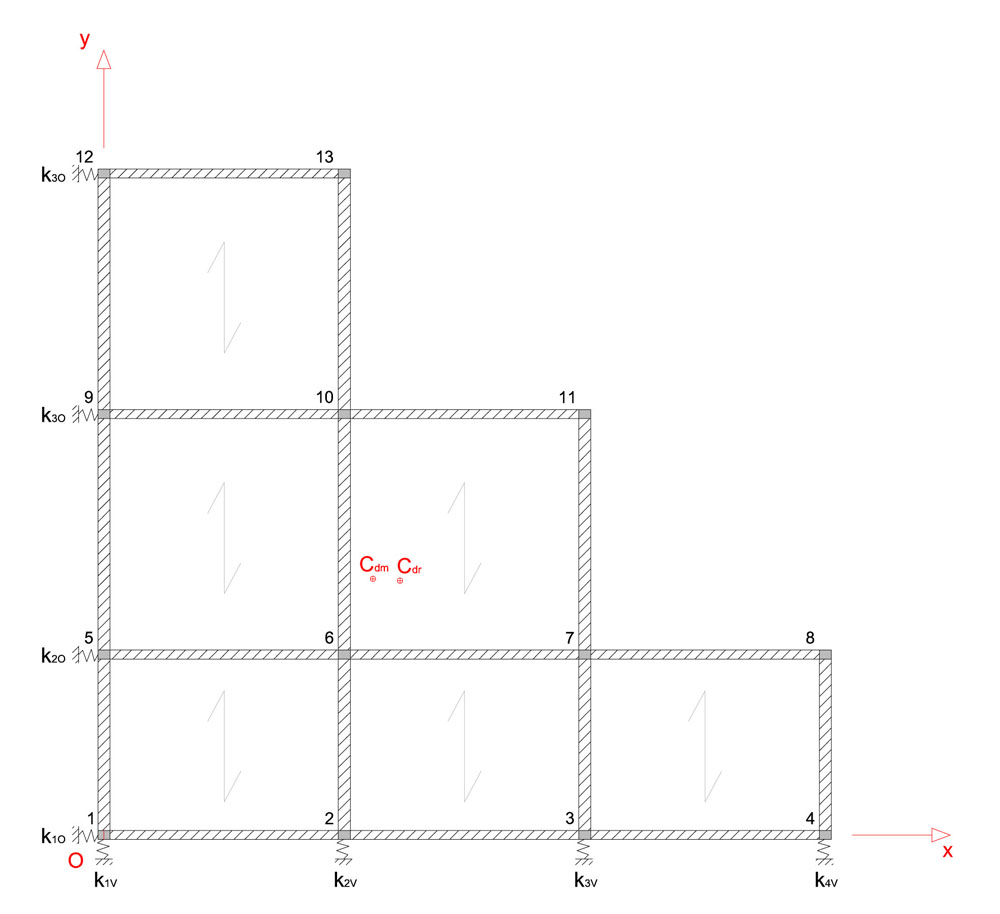
Per un edificio a un solo livello, si consideri la pianta strutturale dell’impalcato:

La struttura tridimensionale è sottoposta a carichi verticali ed azioni orizzontali, quest’ultime interpretabili come sismiche.

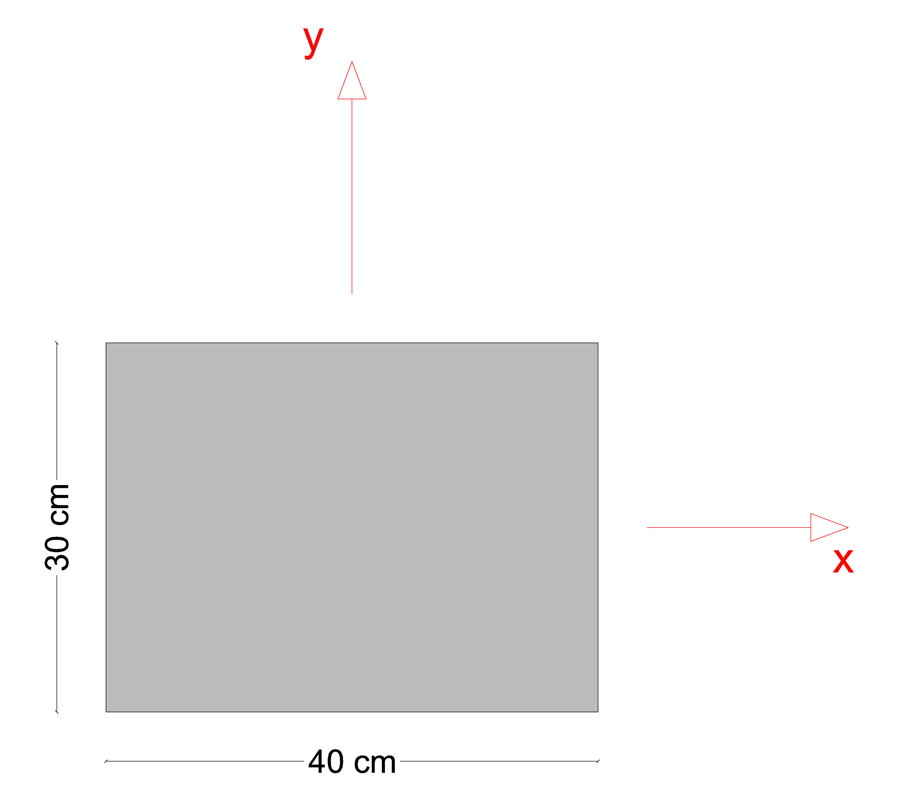
I pilastri in calcestruzzo vengono considerati con sezione rettangolare di base b=40 cm e altezza h=30 cm:

L’impalcato descrive la presenza di 8 telai piani,

4 lungo l’asse x, piano x-z:

1_O) 1-2-3-4

2_O) 5-6-7-8

3_O) 9-10-11

4_O) 12-13

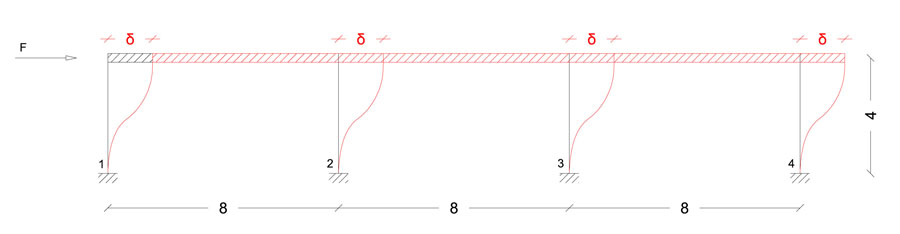
telaio 1_O

 e 4 lungo l’asse y, piano y-z:

1_V) 1-5-9-12

2_V) 2-6-10-13

3_V) 3-7-11

4_V) 4-8

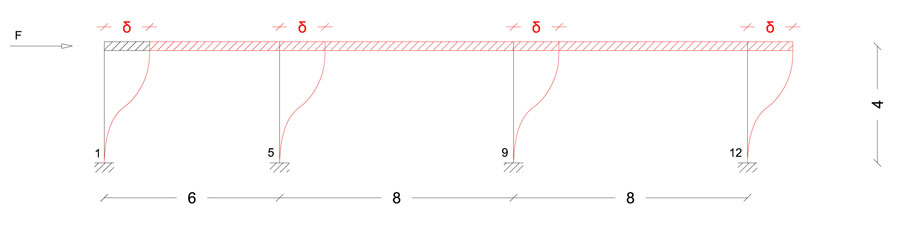
telaio 1_V

che hanno il ruolo di sostenere il peso della costruzione ma anche di reagire alle forze orizzontali agenti sul piano x-y.

Associando quindi il comportamento di questi telai fungenti da controventi a quello dei telai shear-type, per solaio sufficientemente rigido e pilastri elastici, si rappresentano i controventi applicati alla costruzione grazie a delle molle di adeguata rigidezza sul piano x-y.

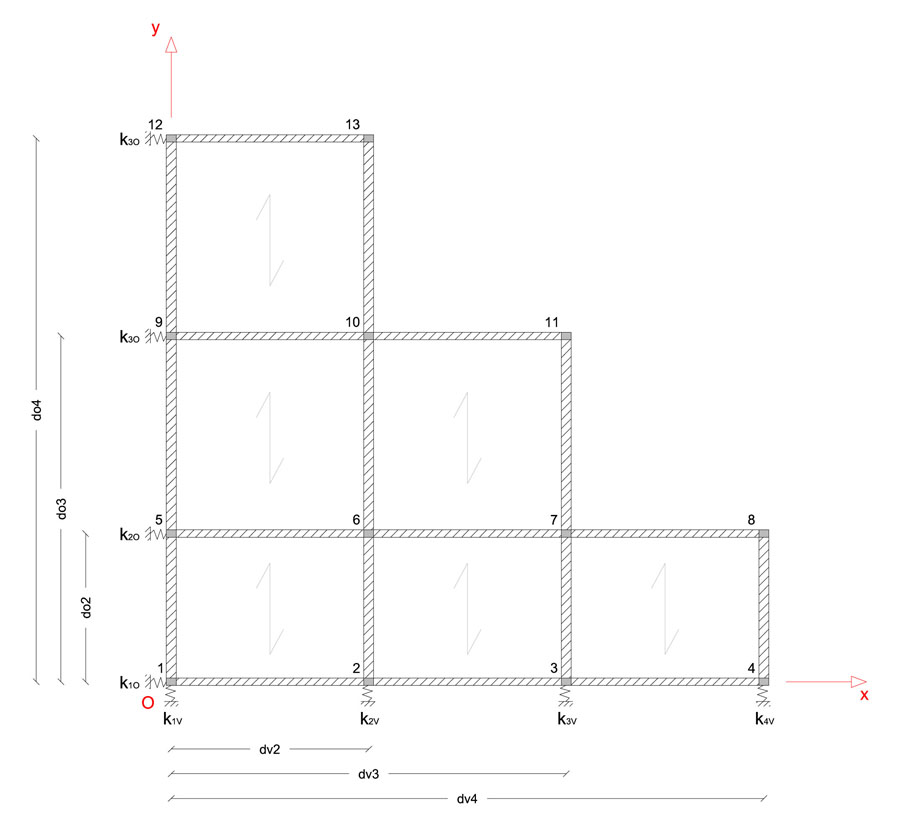
La ridistribuzione delle forze sismiche avviene seguendo una sequenza di passaggi:

1) calcolo delle rigidezze traslanti dei controventi;

2) calcolo del centro di massa;

3) calcolo del centro delle rigidezze;

4) calcolo delle rigidezze globali;

5)calcolo delle forze sismiche;

6) ridistribuzione delle forze sismiche lungo gli assi di riferimento x e y.

1_ calcolo delle rigidezze traslanti dei controventi.

Il valore della rigidezza traslante è valutabile grazie al modulo di Young E= 210 000 N/mm^2, all’altezza dei pilastri h=4,00 m, e ai momenti di inerzia dei pilastri di sezione rettangolare, per cui I=(bh^3)/(12)=(40cm*(30cm)^3)/12=90000cm^4.

Rigidezza traslante dei telai orizzontali:

es: telaio 1:

Rigidezza traslante dei telai verticali:

2_ Calcolo del centro di massa

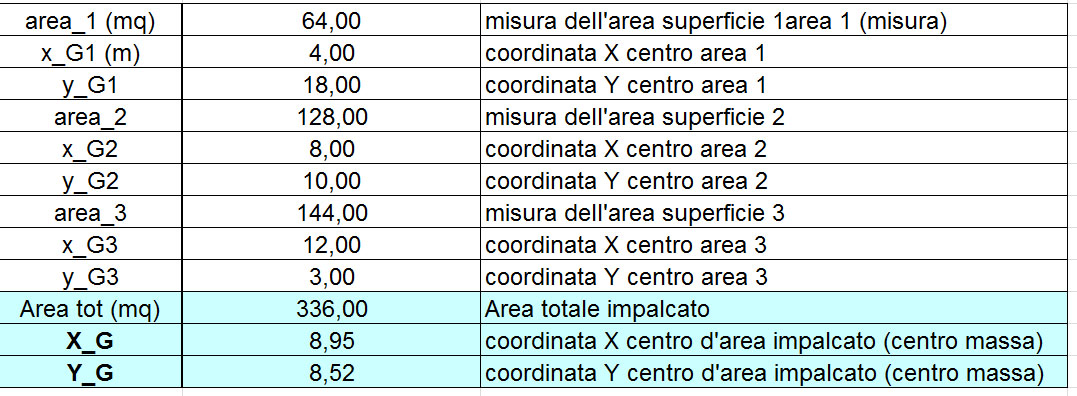
Per il calcolo del centro di massa è possibile immaginare di dividere la struttura in aree rettangolari, valutare il centro di ognuna e poi determinare quello complessivo.

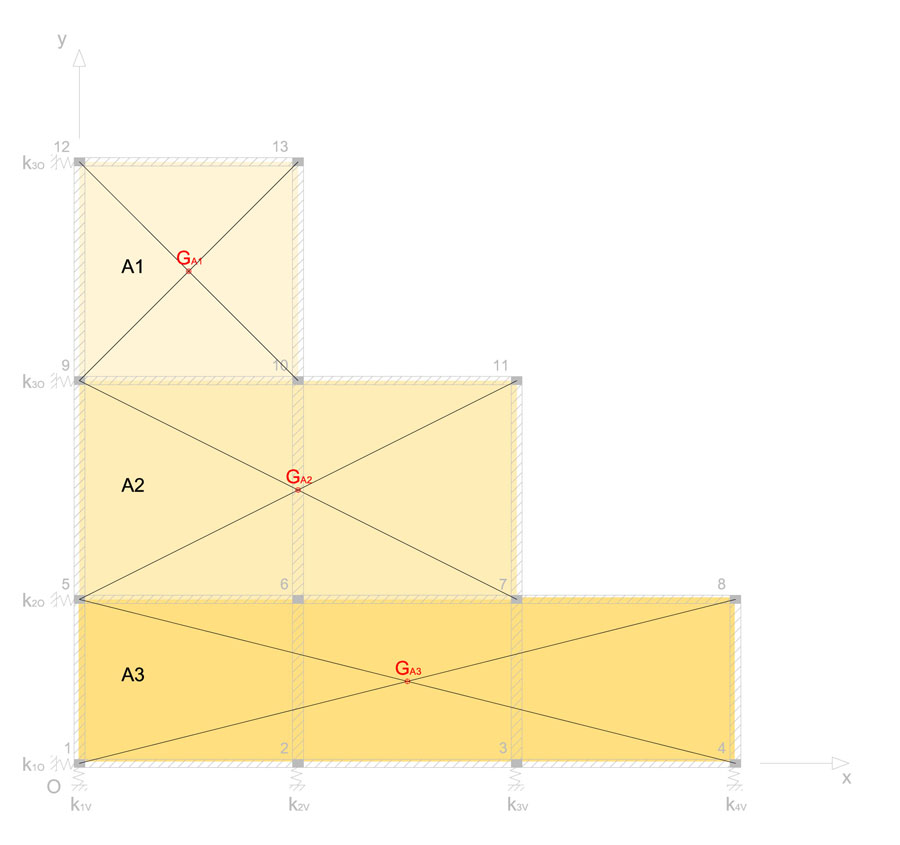
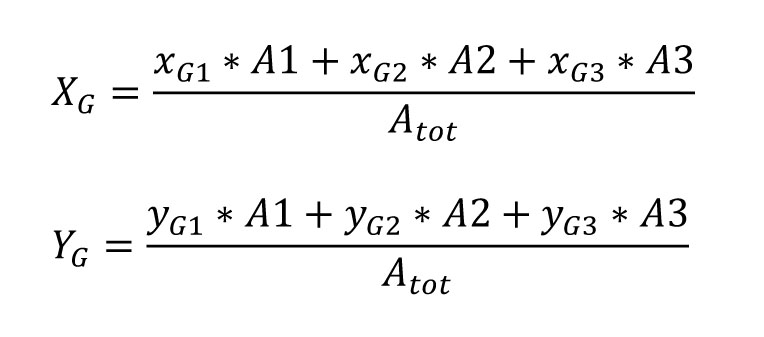
3_ Calcolo del centro delle rigidezze

Il centro delle rigidezze invece richiede le distanze dv e do dei controventi dal centro degli assi di riferimento O e le rigidezze di ogni controventokv e ko, la cui somma definisce la rigidezza totale k_vtot lungo i due assi.

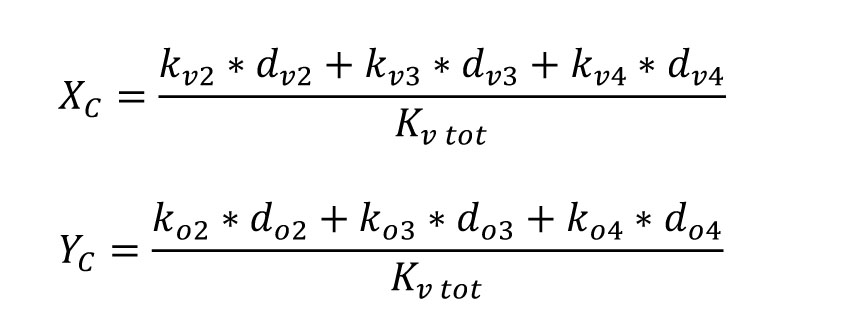
4_Calcolo della rigidezza torsionale totale:

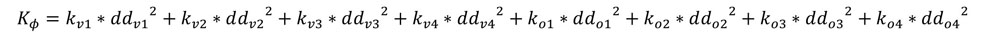
con dd_on e dd_vn distanze dei controventi dal centro delle rigidezze:

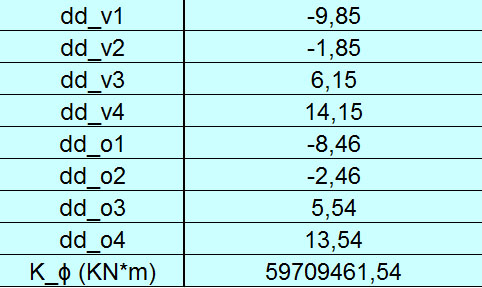
5_Calcolo delle forze sismiche

Dopo aver assegnato i carichi permanenti strutturali e accidentali, è possibile, grazie al coefficiente di intensità sismica

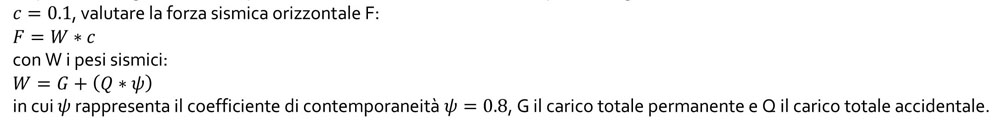
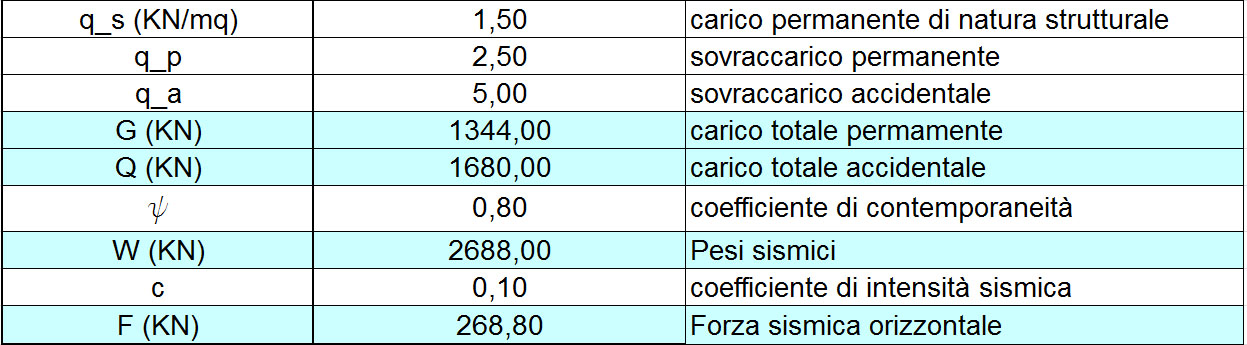
6a_ Ridistribuzione delle forze sismiche lungo x

La ridistribuzione delle forze sismiche richiede la conoscenza del momento torcente M, delle traslazioni u_o e v_o e delle rotazioni dell'impalcato.

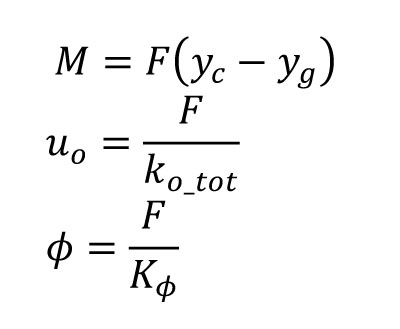
Forze sui controventi verticali:

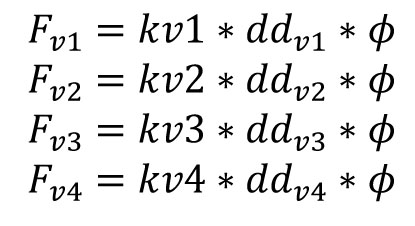
Forze sui controventi orizzontali:

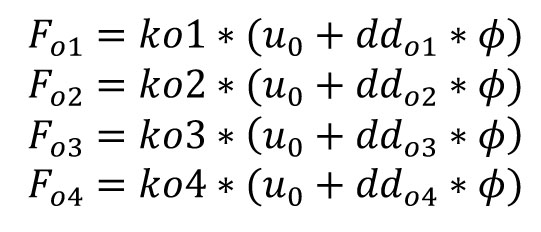
6b_ Ridistribuzione delle forze sismiche lungo y