ESERCITAZIONE VII: Rigidezza torsionale

Inviato da marco.neri il Mar, 25/06/2013 - 17:05

ABSTRACT: La seguente esercitazione si occuperà di analizzare attraverso il calcolo manuale gli effetti della torsione all'interno di una semplice struttura iperstatica in 3 dimensioni e la verifica del risultato all'interno di SAP2000. La torsione nasce quando momenti uguali e opposti agiscono su piani di sezione presi lungo l'asse della trave: l'effetto sarà per l'appunto una deformazione torcente della trave stessa, la quale risponde a tale deformazione attraverso la sua rigidezza torsionale Rt che dipende dal modulo di elasticità tangenziale G, dalla lunghezza l della trave e dal momento d'inerzia torsionale It.

L'esercitazione consisterò proprio nel valutare gli effetti di Rt=G . It / l

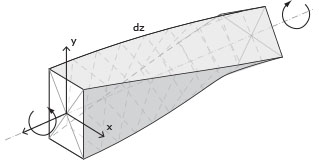
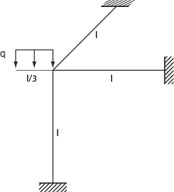
La struttura presa in considerazione ha vincoli ad incastro lungo le sue estremità tranne per una dove si realizza uno sbalzo sul quale è applicato un carico distribuito q.

La struttura complessivamente è iperstatica poichè in 3 dimensioni ogni incastro a 6 gradi di vincolo mentre l'isostaticità è garantita da 6. Ne segue che la struttura è 18-6 = 12 volte iperstatica.

Lo sbalzo invece è di per se isostatico (è visibile come una mensola incastrata e risponde alle stesse azioni interne ed esterne). Può essere sostituito quindi ai fini dell'esercitazione come da figura:

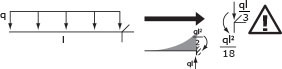
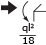
ma ricordiamo che per il modello di
trave adottato non abbiamo
deformabilità assiale perciò

 

Ricordando lo schema noto

e la resistenza alla torsione come Rt=G . It / l e il momento torcente come M= Rt φ

Se la deformata per le travi sul piano ZY incastrate è la seguente

allora l'equilibrio al nodo sarà

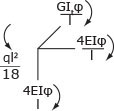
la cui equazione è ql2/18 = (4EI/l + 4EI/l + GIt/l) φ
⇒ φ=ql2/18R con R=4EI/l + 4EI/l + GIt/l

Per le travi dunque si avrà che i momenti flettenti sono per quelle inflesse M=4EI/l . 1/R . ql2/18
mentre per quella soggetta a momento torcente Mt=GIt/l .1/R . ql2/18
(che rispettivamente per la scelta della struttura con travi di uguale lunghezza diventano M=2/9EI .1/R . ql e Mt=GIt/18 .1/R . ql)

Assegnazione di profili e verifica su SAP2000

luce travi l = 1m

q=18 KN/m ⇒ q(l/3)2/2 = 18 . 1/9 . 1/2= KN m

NB le misure sono espresse in KN e m per un confronto più rapido con SAP

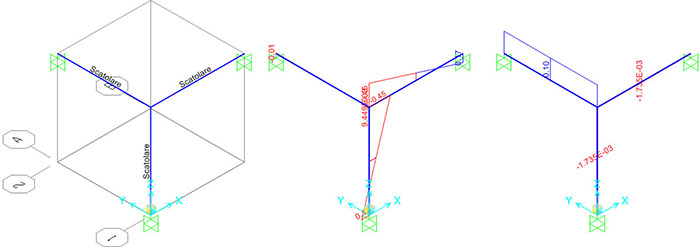
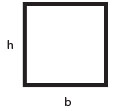
Scatolare in acciaio
h=b=0,2 m=a
t=0,007 m
I=bh3/12-b(h-t)3/12=
= 3.359 10-4 m4
It=4Ω2s / lm=
=4(a2)2 s / 4a = a3s =
=5.032 10-5m4 

E=2,1 108 KN/m2
G=8 107 KN/m2

M=0.457 KN m
Mt=0.085 KN m

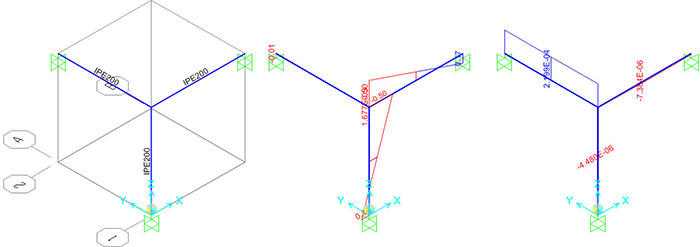
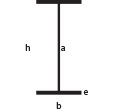
IPE200
h=0,2 m b=0,1 m
a=0,0056 m e=0,0085 m
I= 1,42 10-6 m4
It=5,164 10-8 m4

E=2,1 108 KN/m2
G=8 107 KN/m2

M=0.4991 KN m
Mt=0.0017 KN m

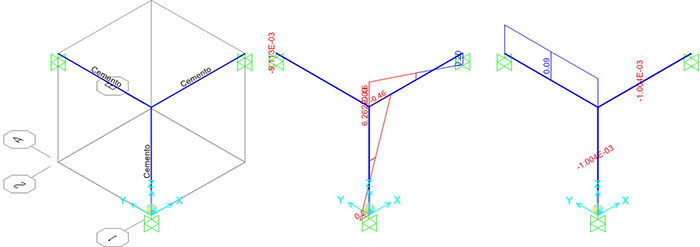
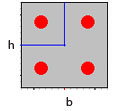
Profilo in CLS(valori SAP)
h=b=0,2 m
I=1.333 10-4 m4
It=2.253 10-4 m4

E=2,485 107 KN/m2
G=1.035 107 KN/m2

M=0.5000 KN m
Mt=0.0801 KN m

NB una volta inseriti i valori metrici base delle sezioni le informazioni su quelli derivati e sui materiali sono visualizzabili dai pannelli contestuali di SAP attraverso le schermate Section Properties e il + vicino il pannello Material

RISULTATI SAP