ESERCITAZIONE VIII: Graticcio

ABSTRACT: Nella seguente esercitazione verrà esposto il modello della struttura a graticcio e gli effetti provocati dall'assenza di gerarchia fra gli elementi lineari che lo compongono. Si risolverà una semplice struttura a graticcio caratterizzata da un nodo a incastro che salda 4 travi a loro volta incastrate. Questa sarà didatticamente utile a comprendere strutture più generiche e relativamente complesse come la seguente.

NB l'aggiunta di appoggi intermedi incrementa le potenzialità meccaniche tuttavia non è strettamente legata ad una disposizione necessariamente regolare

In questa esercitazione si risolverà come accennato nella premessa la seguente struttura:

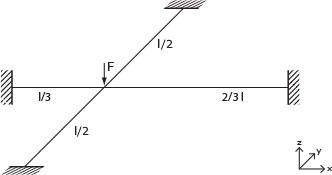
È necessario precisare che sebbene il nodo sia spaziale (deformabile in tutte le direzioni) esso viene considerato indeformabile assialmente dunque v_x≡0 e v_y≡0 per definizione.

Un'analisi preliminare ci porta anche ad eliminare il contributo della rotazione attorno l'asse z. Non vi sono infatti forze capaci di generare un momento attorno a quest'asse (φ_z=0).

Continuando a osservare il nodo possiamo valutare le sue sezioni lungo i piani xz e xy. 

Da queste sezioni valutiamo che la rotazione lungo x per via della simmetria lungo il piano xz è φ_x=0. Al contrario si osserva la presenza di una freccia v_z≠0 e della rotazione lungo y φ_y≠0. Per semplicità d'ora in avanti chiamerò v_z=δ e φ_y=φ.

Noti gli schemi:

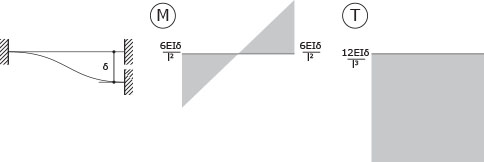
ed essendo il problema lineare, gli effetti possono essere sommati. Ragionando prima sulle azioni provocate dall'abbassamento e poi dalla rotazione del nodo saremo in grado di conoscere il comportamento complessivo ed individuare δ e φ.

ABBASSAMENTO

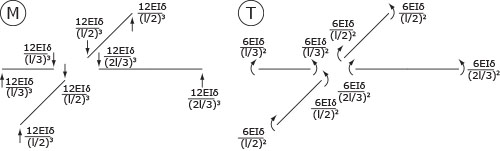
TORSIONE / ROTAZIONE

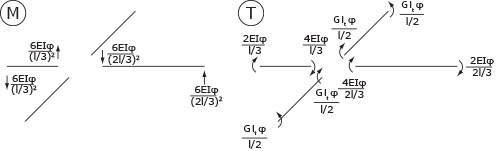
da queste l'equilibrio del nodo.

EQL ALLA TRASLAZIONE

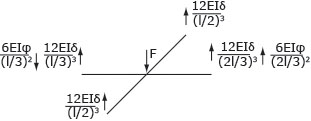
F - 12EIδ/(l/2)³ - 12EIδ/(l/2)³ - 12EIδ/(l/3)³ - 24EIδ/(2l/3)³ -  6EIφ/(l/3)² + 6EIφ/(2l/3)²= 0

EQL ALLA ROTAZIONE

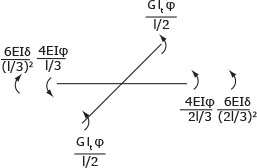
6EIδ/(2l/3)² - 6EIδ/(l/3)² + 4EIφ/(l/3) +4EIφ/(2l/3) + GI_tφ/(l/2) + GI_tφ/(l/2) = 0

Razionaliziamo quest'ultima equazione:

φ(12EI/l + 6EI/l + 4GI_tφ/l ) + δ(-54EI/l² - 27/2 ^. EI/l²) = 0
⇒φ(18EI + 4GI_tφ )^.(EI/EI)/ l + δEI/l²(-81/2) = 0
⇒φ(18+ 4GI_tφ/EI )EI + δEI/l(-81/2) = 0, α = GI_t/EI ⇒ φ(18+ 4α ) = 81/2 ^. δ/l

⇒δ/l=φ(36+8α)/81

Mentre la prima:

F - 192 EIδ/l³ - 324 EIδ/l³ - 81/2 ^. EI δ/l³ - 27/2 ^. EI φ/l² + 54 EI φ/l²= 0
⇒Fl²/EI- 192 δ/l - 324 δ/l - 81/2 ^. δ/l - 27/2 ^. φ + 54 φ= 0
⇒Fl²/EI- 1113/2 ^. δ/l - 81/2 ^. φ = 0 ⇒Fl²/EI- 1113/2 ^. φ(36+8α)/81 - 81/2 ^. φ = 0

⇒Fl²/EI = 371/27 ^. (18+4α)φ - 81/2 ^. φ = φ (371^.18/26 - 81/2 + 371^.4/27α )

⇒ φ (1241/6 + 1486/27 GI_tφ/EI )= Fl²/EI
⇒ φ = Fl² / (1241/6 EI + 1486/27 GI_t )

Mentre:

δ= (Fl³ (36+8GI_t/EI ) ) / (1241/6 EI + 1486/27 GI_t )

con un profilo IPE200 e F=10KN, l=1m

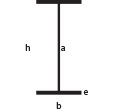
h=0,2 m b=0,1 m
a=0,0056 m e=0,0085 m
I= 1,42 10^-6 m⁴
I_t=5,164 10^-8 m⁴
E=2,1 10⁸ KN/m²
G=8 10⁷ KN/m²

δ= 7.2 10^-5 m, φ =1.6 10^-4

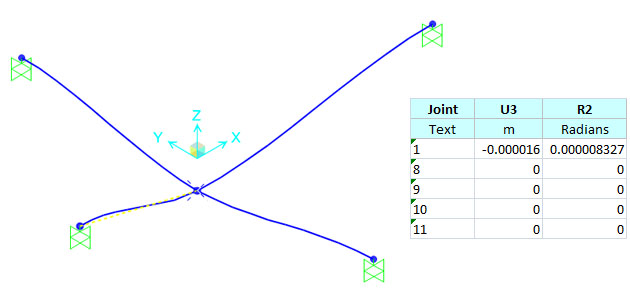
Dalla deformata e i dati esportati da SAP2000 è così convalidata la bontà dei risultati: