Esercitazione_9.0 graticcio di travi (risoluzione a mano e tramite software SAP2000)

 

Esercitazione_9.0

graticcio di travi (risoluzione a mano e tramite software SAP2000)

 

1_

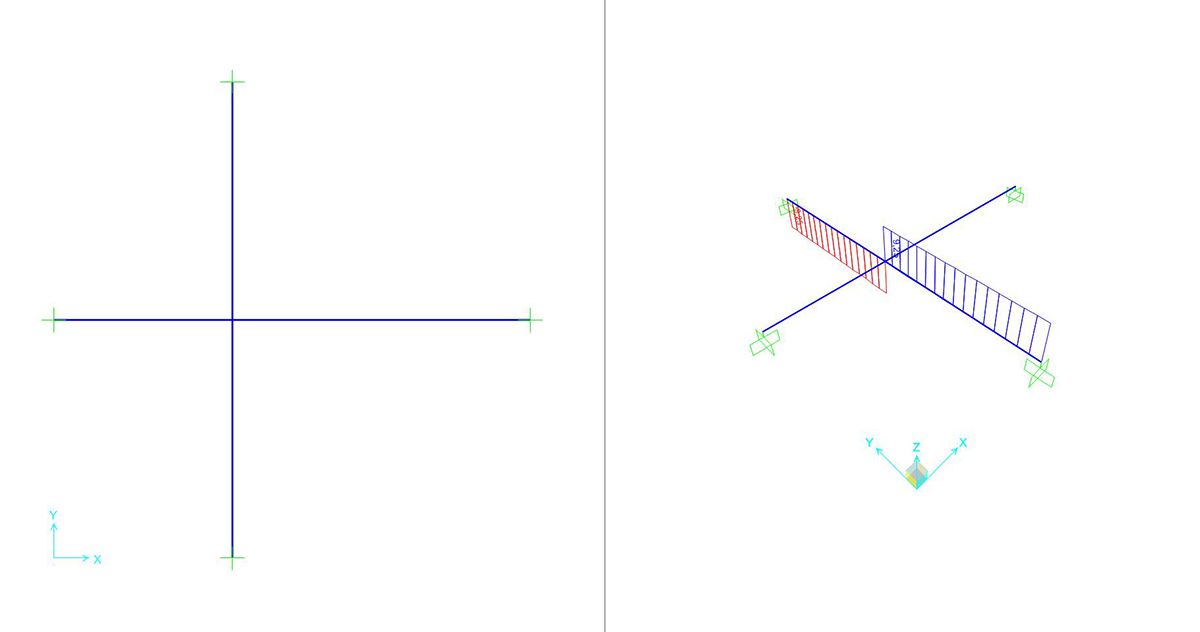
Il sistema proposto risulta essere un sistema tridimensionale composto da travi aventi la stessa sezione di lunghezza 12m con una forza puntuale pari a 100 kN. Lo scopo dello studio del sistema risulta essere quello di comprendere il funzionamento del sistema a graticcio e come il nodo 1 si abbassa e ruota in funzione della forza applicata, lo studio successivamente verrà incentrato sulla sezione ed il materiale della trave soggetta a torsione, per comprendere come quest’ultimi influiscano a parità di azioni esterne.

 

 

 

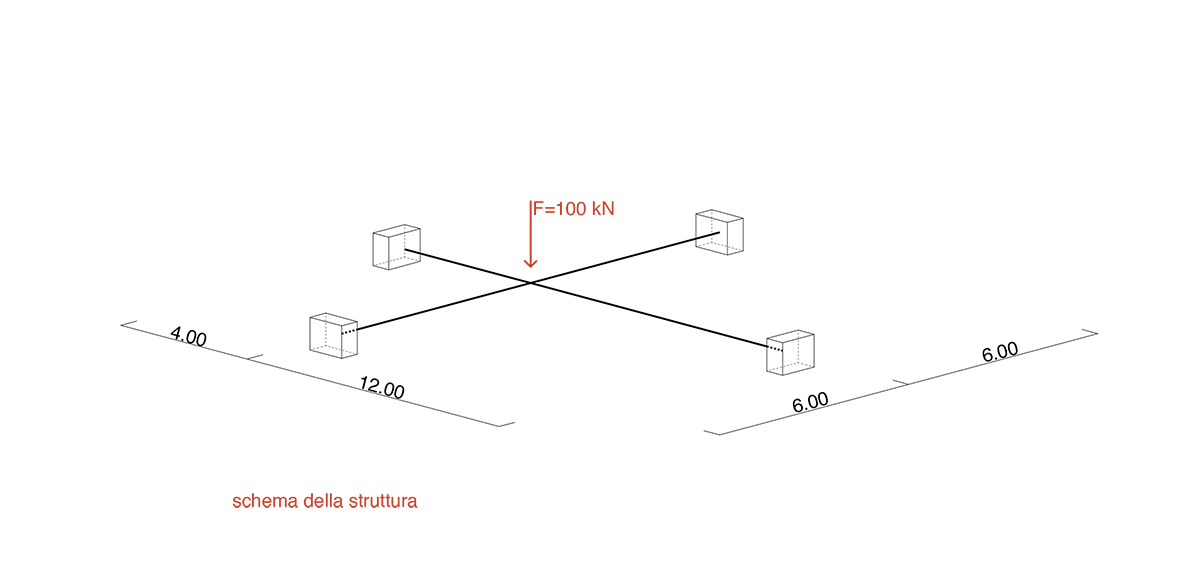
2_

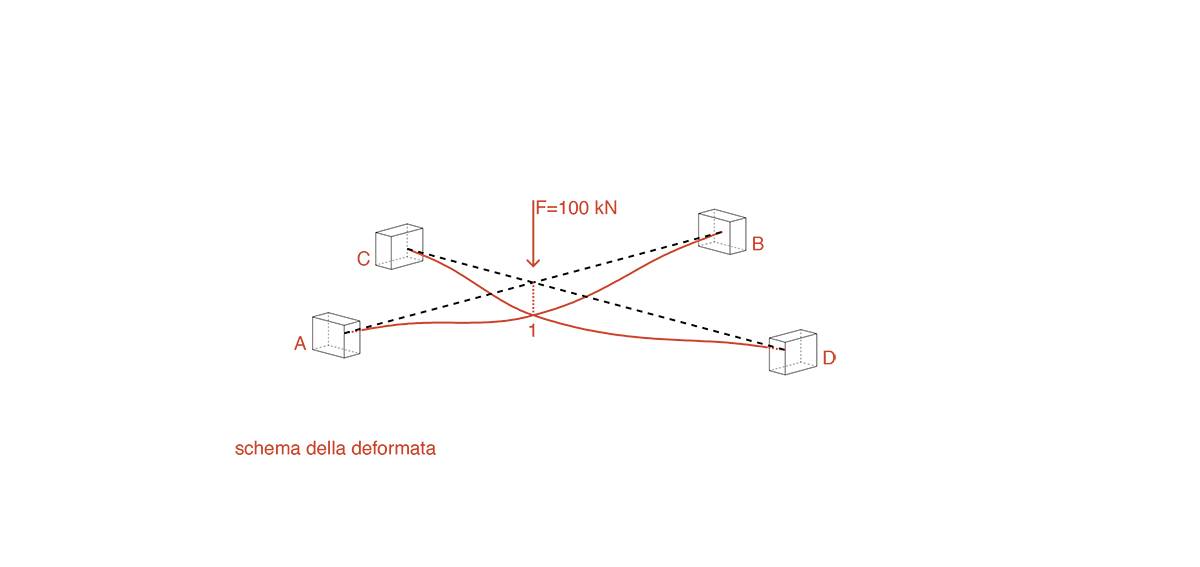
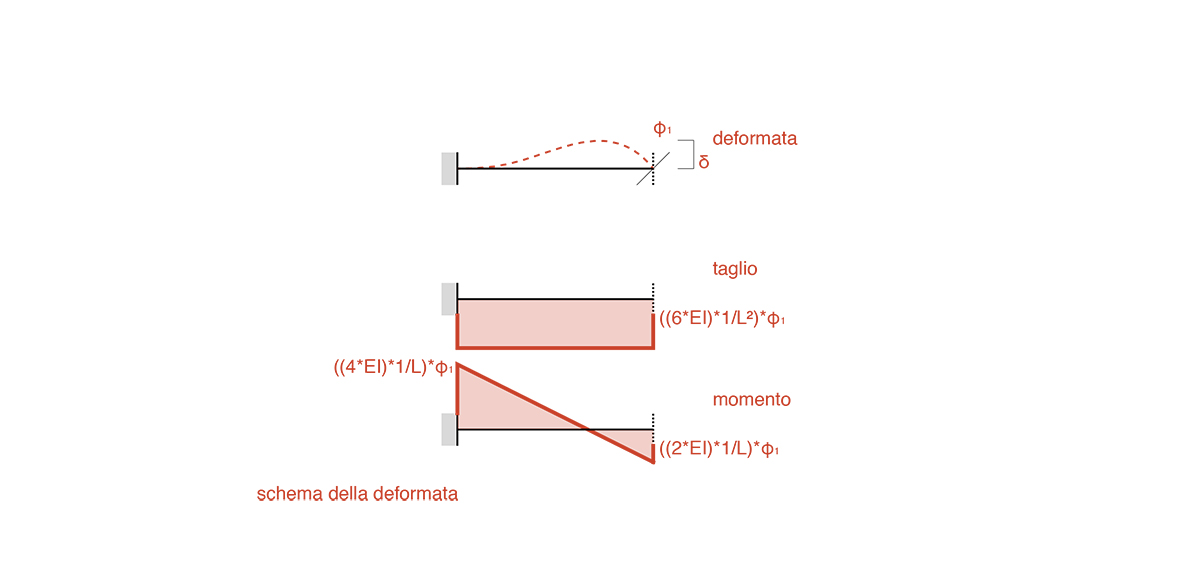
Per poter studiare la struttura in maniera più semplice, quest’ultima viene studiata attraverso gli schemi notevoli dei diagrammi della deformata. Lo schema presenta però una complicazione, in quanto il nodo 1 non risulta essere posizionato in mezzeria, quindi la forza applicata genera una rotazione φ1. Studiando di conseguenza le due travi della struttura, si può comprendere come la rotazione φ1 della trave CD dovrà necessariamente essere uguale all’abbassamento δ della trave AB. Da questo si può dedurre che sulla trave CD sono presenti due tipi di deformazioni (la rotazione φ1 e l’abbassamento δ), mentre sulla trave AB solo quella verticale (δ).

La struttura verrà studiata dividendo le due azioni agenti sulla trave, usando alla fine il metodo della sovrapposizione degli effetti.

 

 

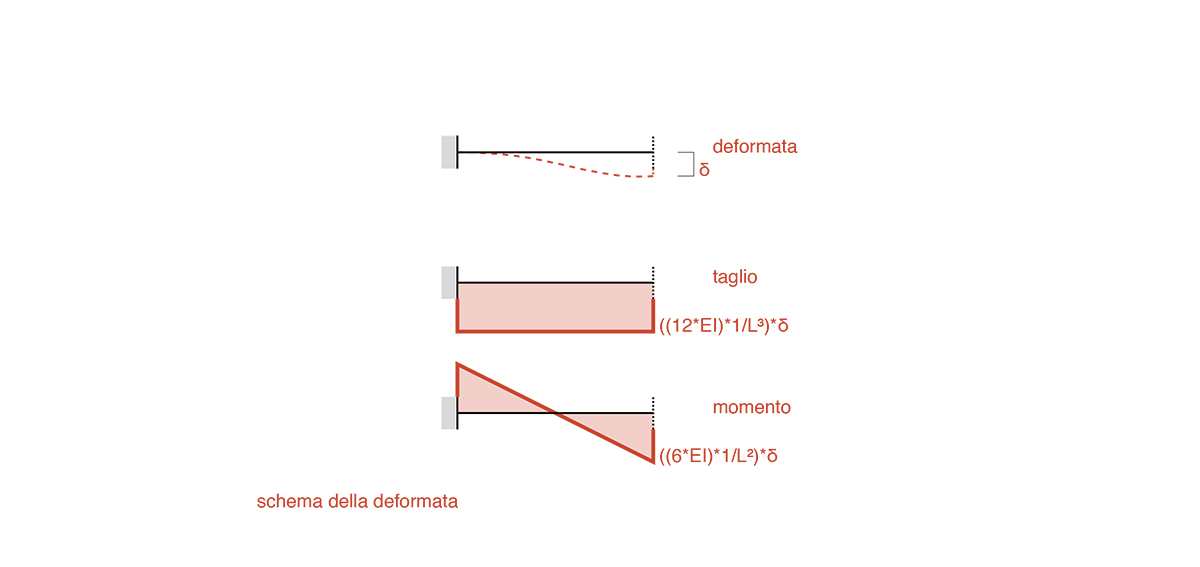
trave AB_abbassamento δ

 

 

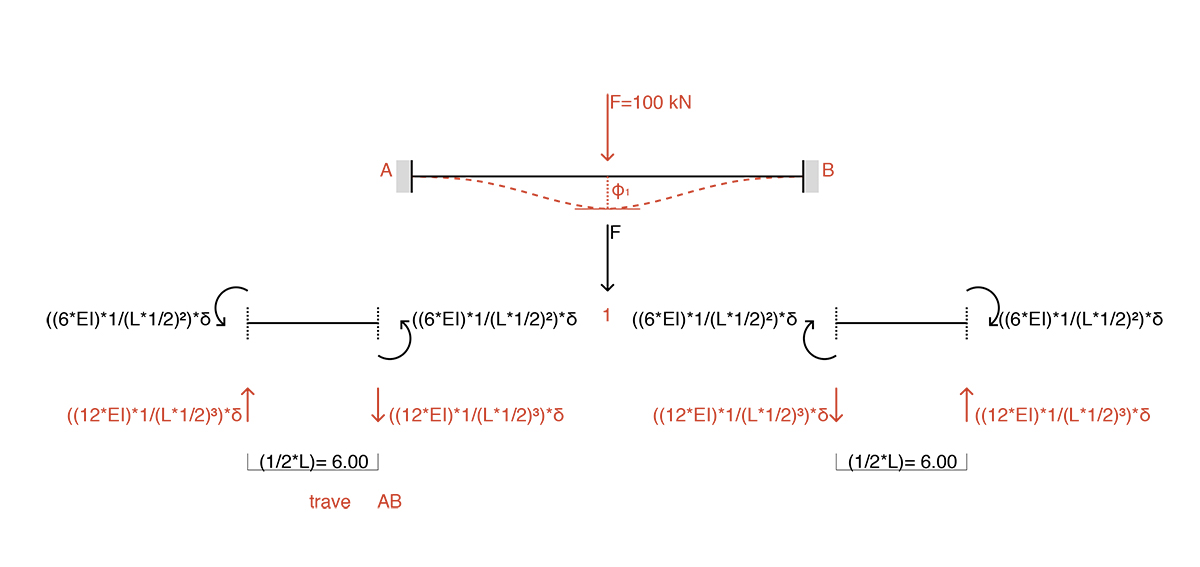
Lo studio dei momenti flettenti per la trave AB, ci fa vedere come quest’ultimi si annullano e quindi di conseguenza non verranno riportati nei calcoli successivi.

 

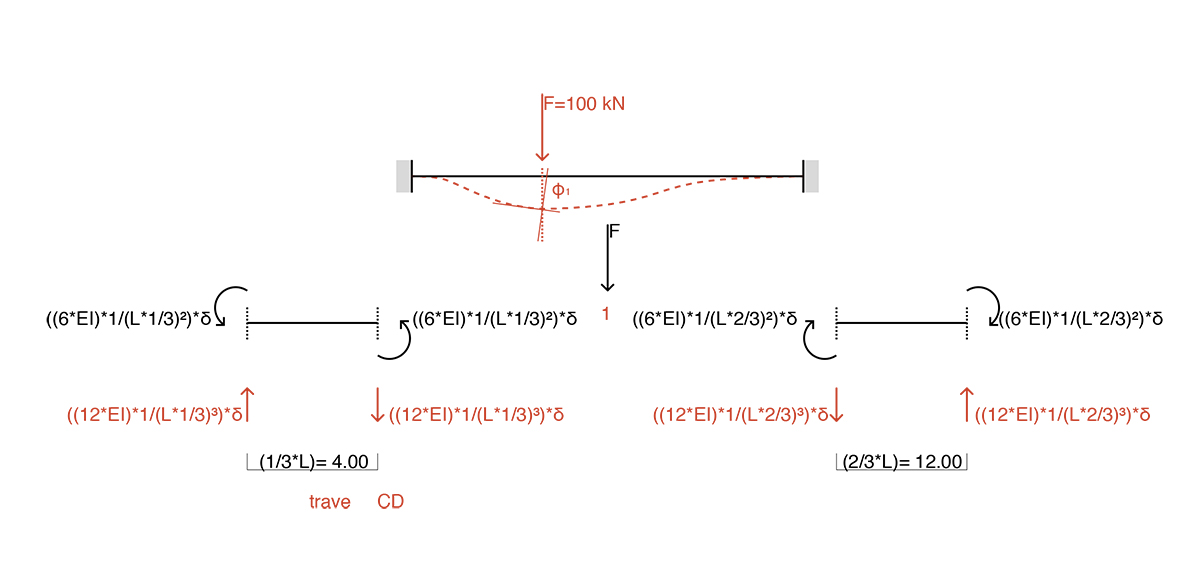
trave CD_abbassamento δ

 

 

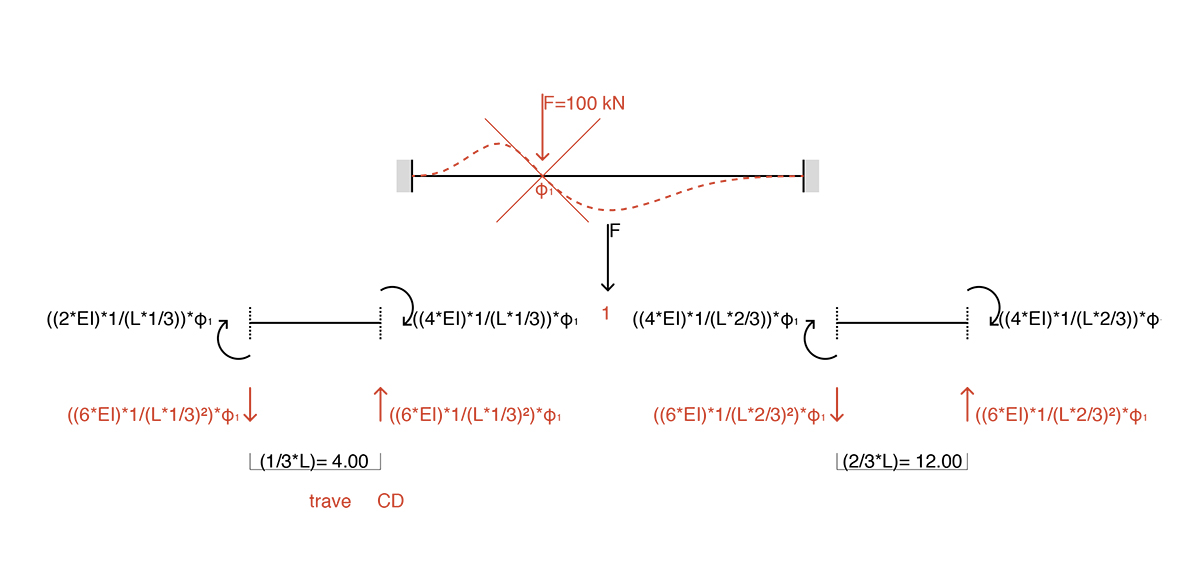
trave CD_rotazione φ1

 

 

 

3_

Come si può dedurre dallo studio eseguito su rotazioni ed abbassamenti si può comprendere come la trave AB presenta solamente una deformazione di abbassamento verticale; ciò nonostante l’inflessione della trave CD genera su di essa un momento torcente. La trave AB quindi reagirà alla sollecitazione prodotta dalla trave CD con un momento torcente di verso opposto alla rotazione definita da quest’ultima.

 

 

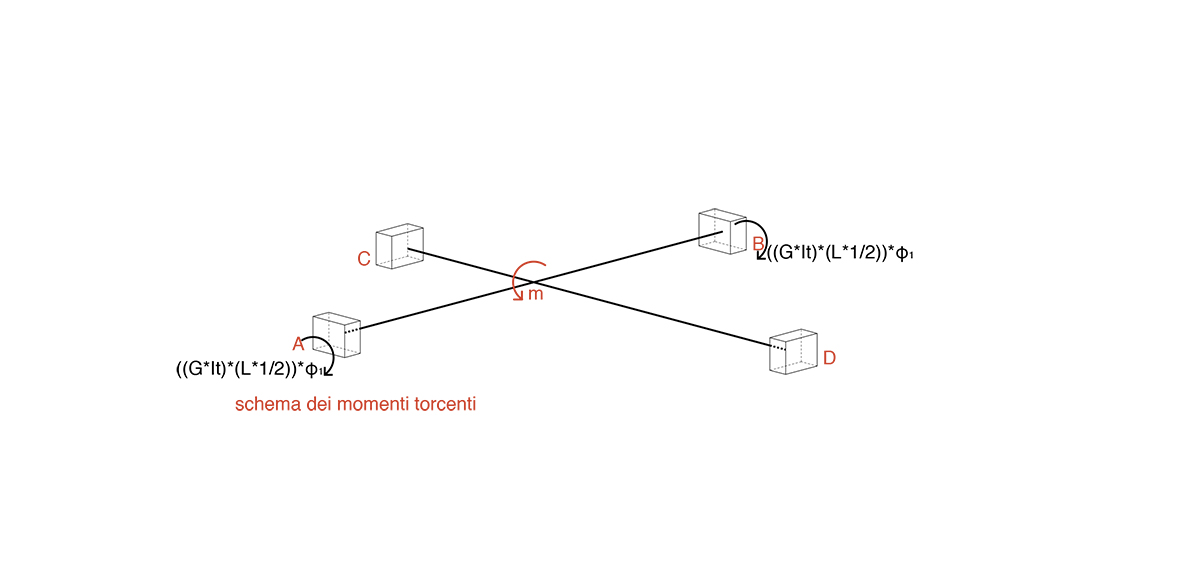
Successivamente si procederà studiando l’equilibrio del nodo 1, inizialmente studiando l’equilibrio alla traslazione verticale e successivamente l’equilibrio alla rotazione.

 

Eq. alla traslazione verticale nodo 1

 

 

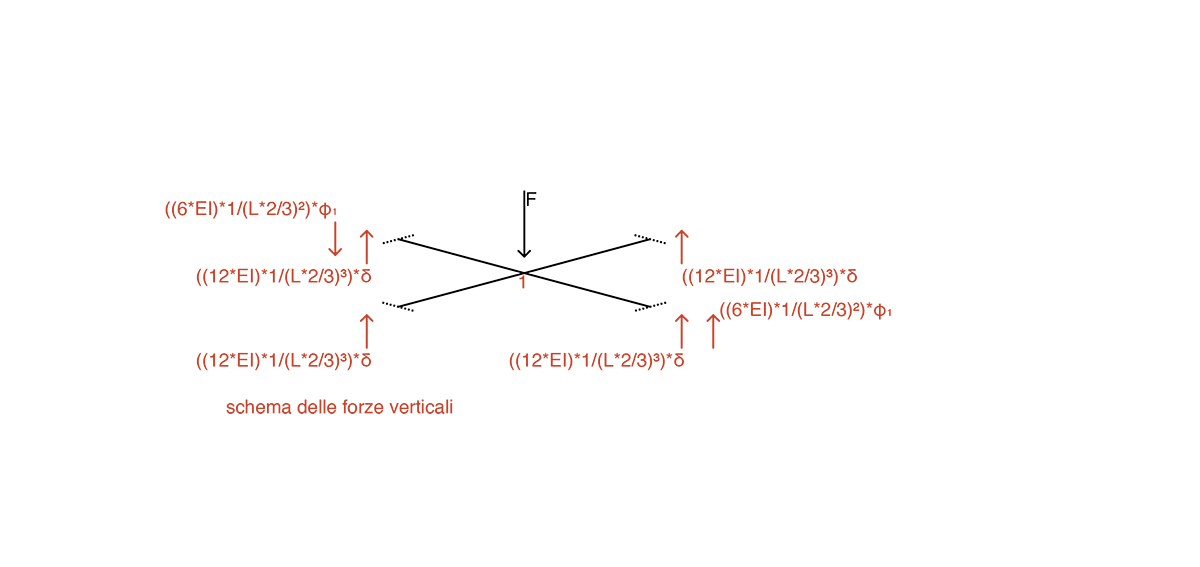
Eq. alla rotazione nodo 1

 

 

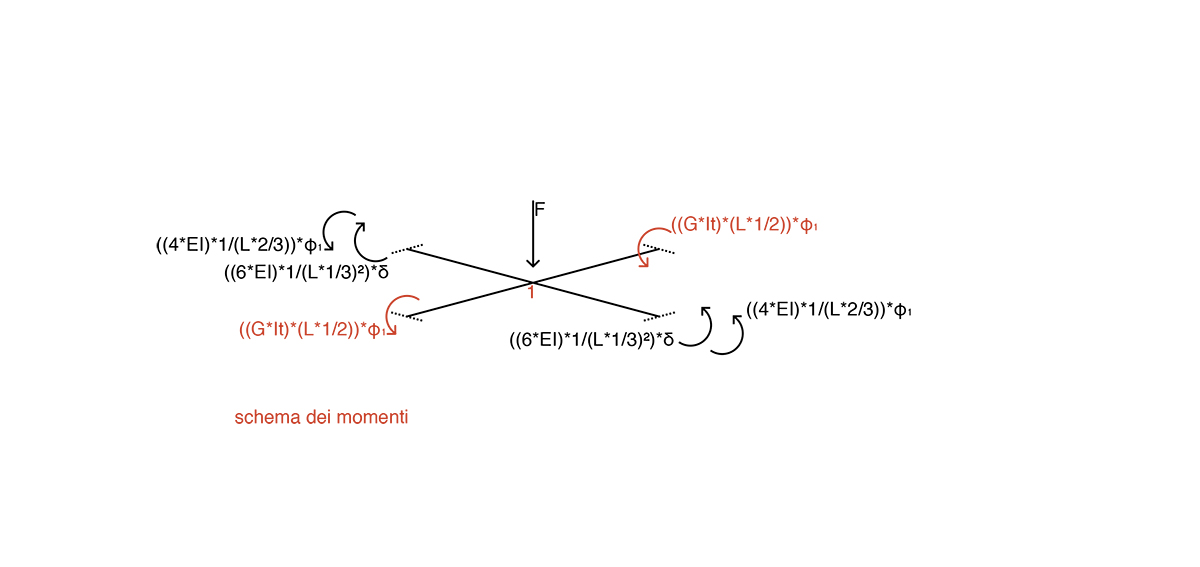
Ci si presenta quindi un sistema di 2 equazioni in 2 incognite.

 

4_

Possiamo ora attraverso un software WolframAlpha (computational knowledge engine) per poter risolvere il sistema:

 

5_

Successivamente alla risoluzione a mano del sistema del nodo si procede con la verifica tramite il software SAP.

 

La modellazione viene effettuata per comodità direttamente in SAP.

creare un nuovo file con una griglia utile al disegno dell’asta:

FILE > NEW MODEL >

 

 

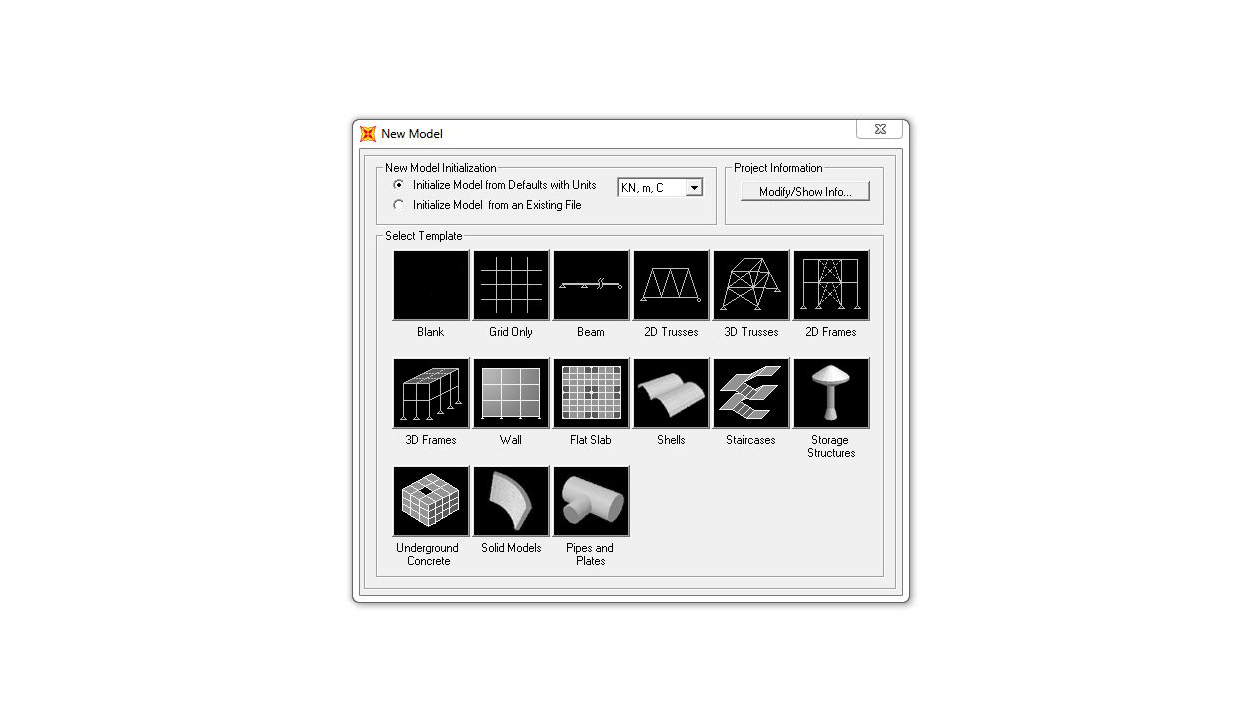
QUICK GRID LINES > impostare 9 assi sull’asse x, 9 sull’asse y e 1 sull’asse z > impostare come GRID SPACING la dimensione che vorremo dare alla lunghezza della trave

 

 

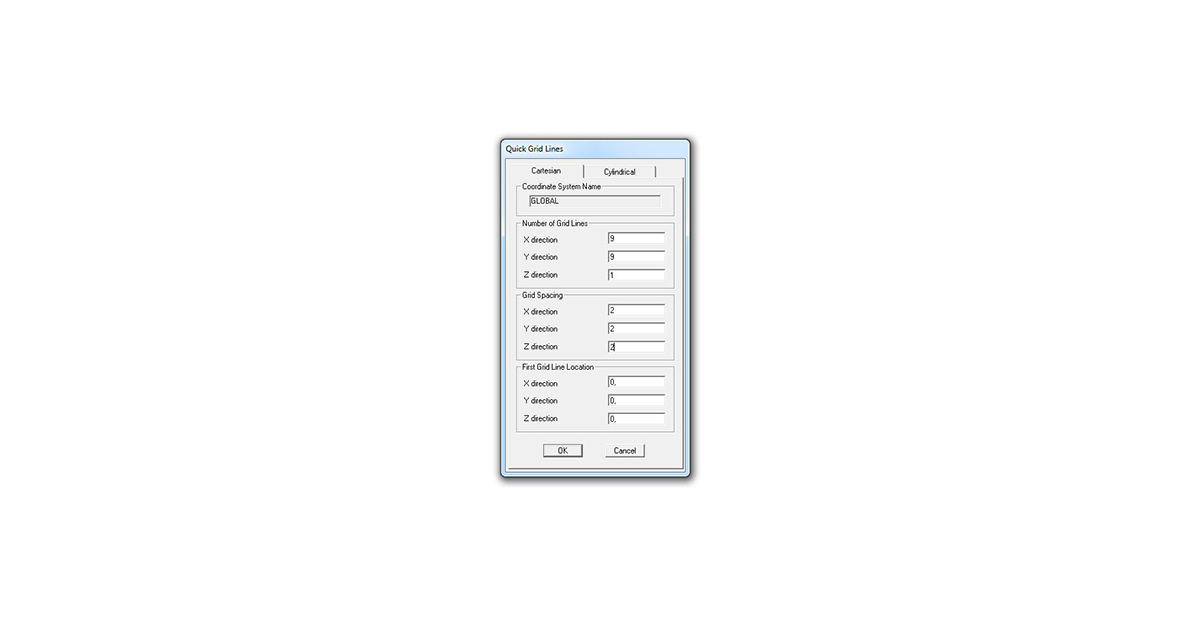
le impostazioni date alla griglia dovrebbero produrre una condizione analoga alla seguente:

 

 

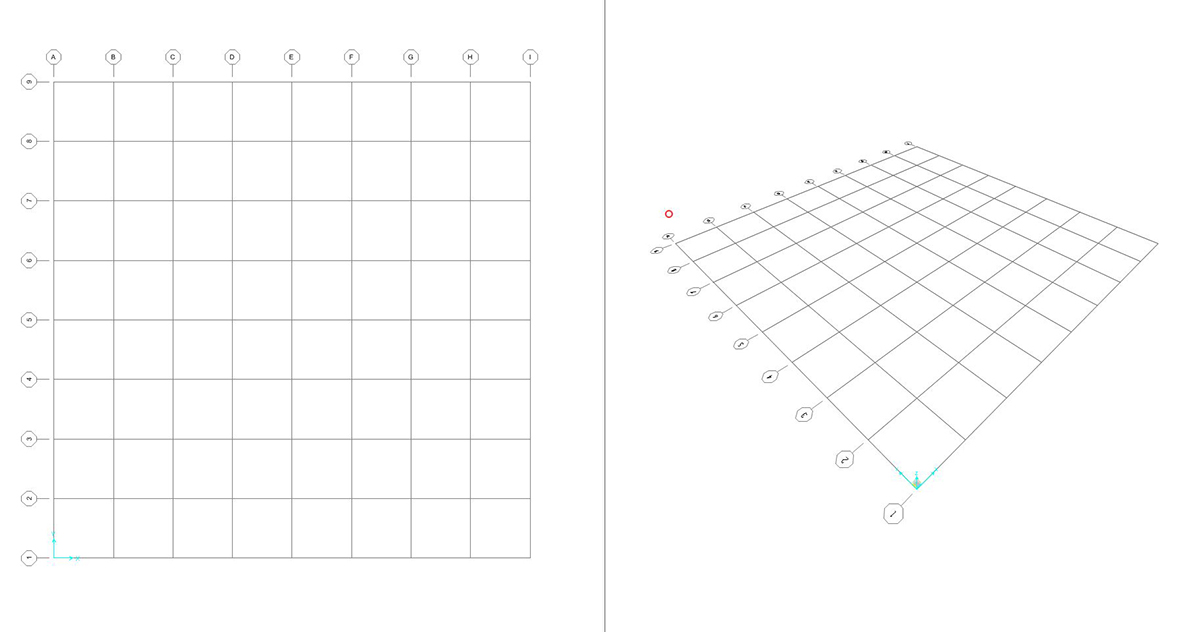
disegnare le aste della trave seguendo la spaziatura della griglia preimpostata.

 

 

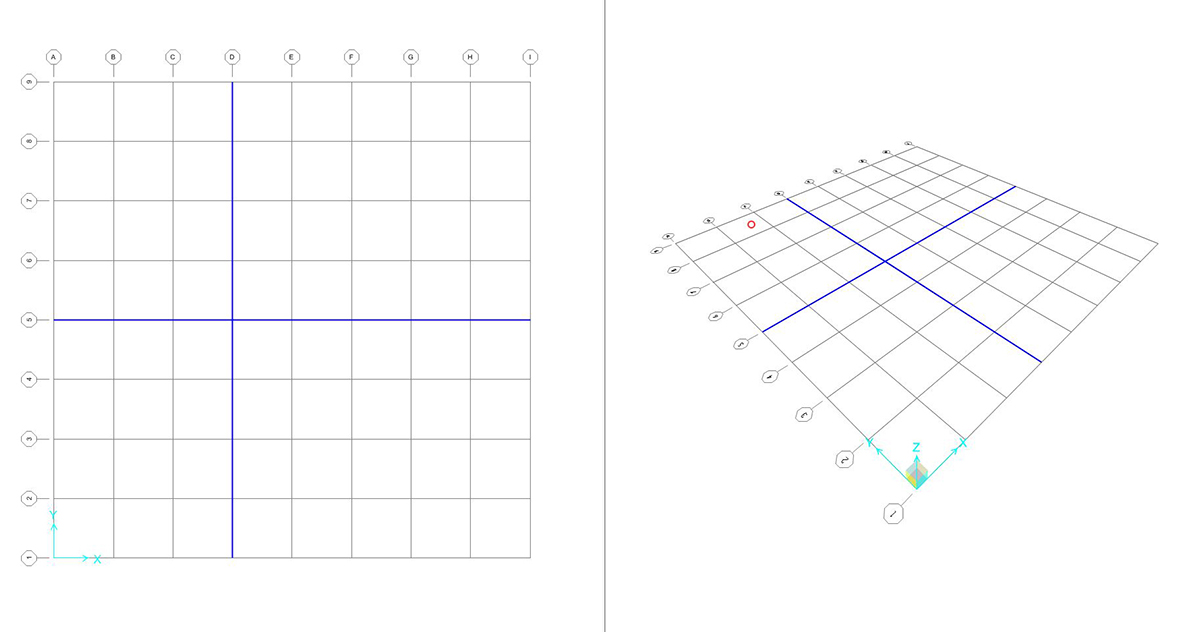
assegnare i vincoli: 

selezionare il punto > ASSIGN > JOINT RESTRAINTS > spuntare le sollecitazioni che il vincolo da posizionare trattiene

 

 

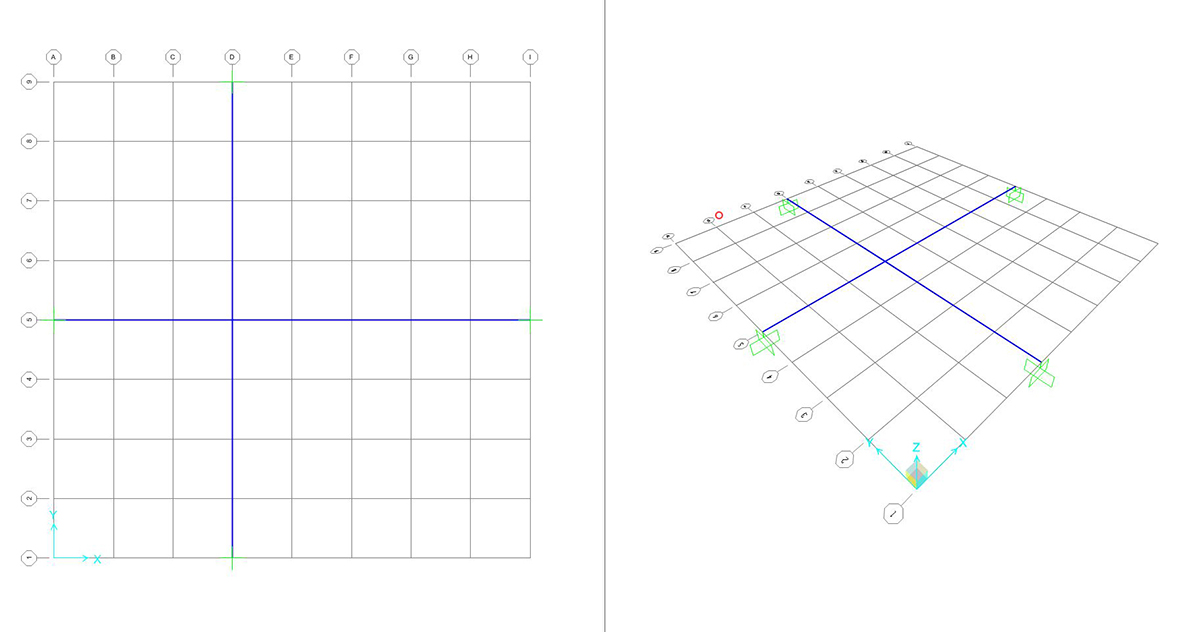
vengono assegnati incastri sulle 4 aste

 

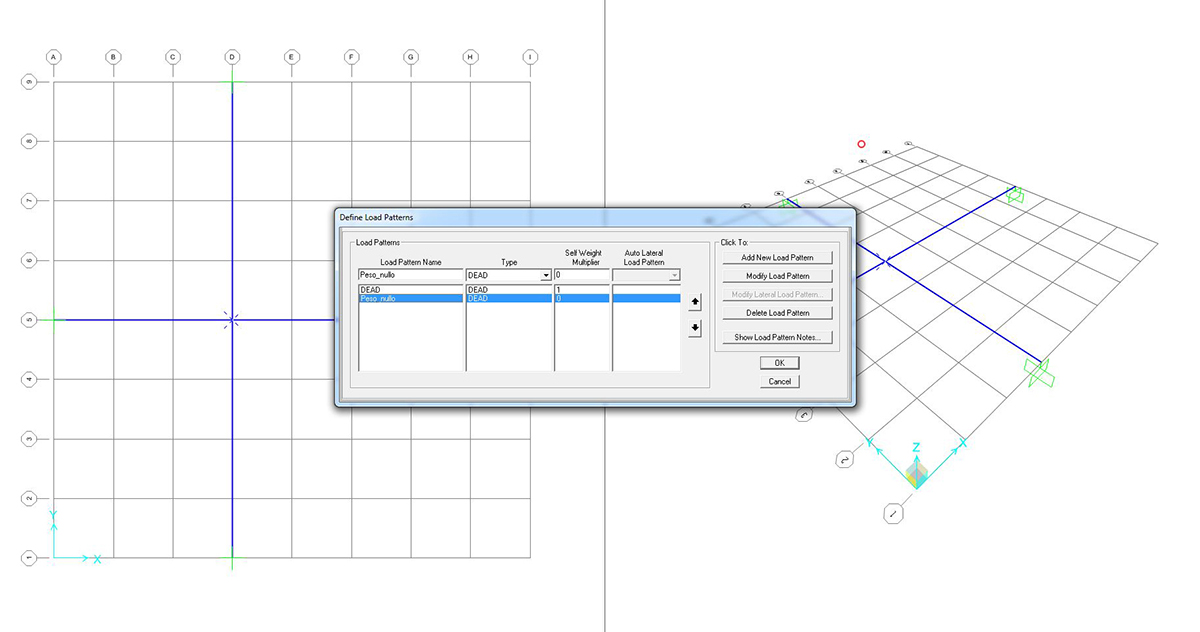
N.B. In questo tipo di esercizi, impostiamo l’analisi in modo che non consideri il peso proprio della struttura (che costituirebbe un carico distribuito su travi che si deve considerare scariche). 

Ciò viene fatto creando un nuovo LOAD PATTERN che abbia 0 come coefficiente di moltiplicazione del carico SELF WEIGHT MULTIPLER.

 

 

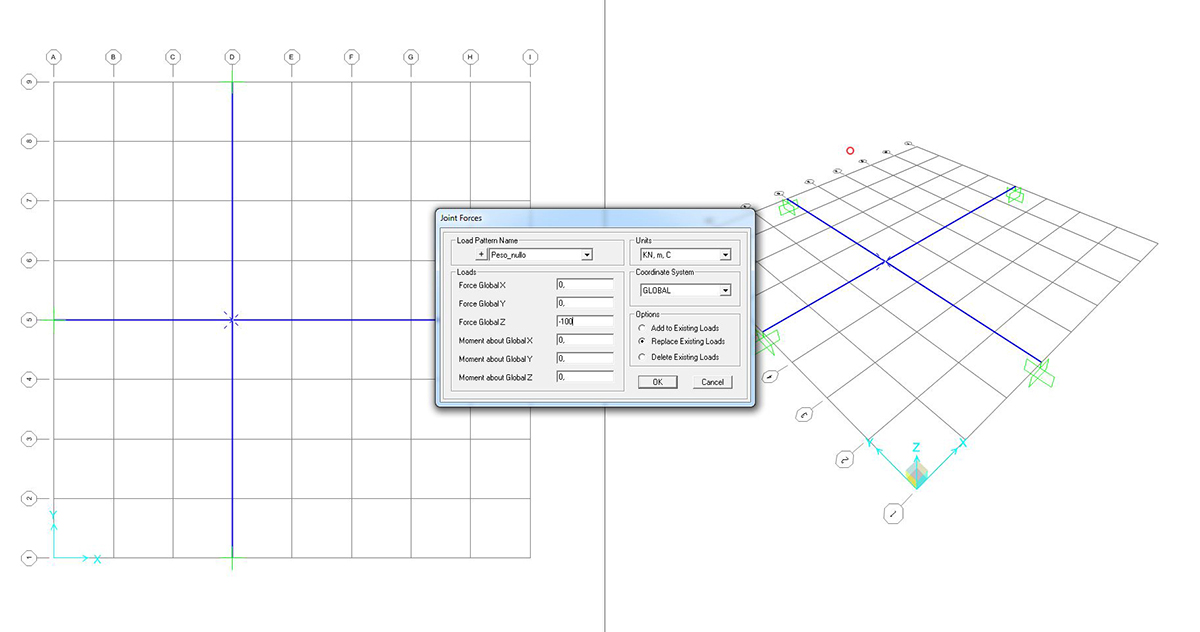
Si procede con l’assegnazione dei carichi con il comando ASSIGN > JOINT LOADS > DISTRIBUTED, trattandosi di un’idealizzazione per la quale i carichi sono distribuiti.

 

 

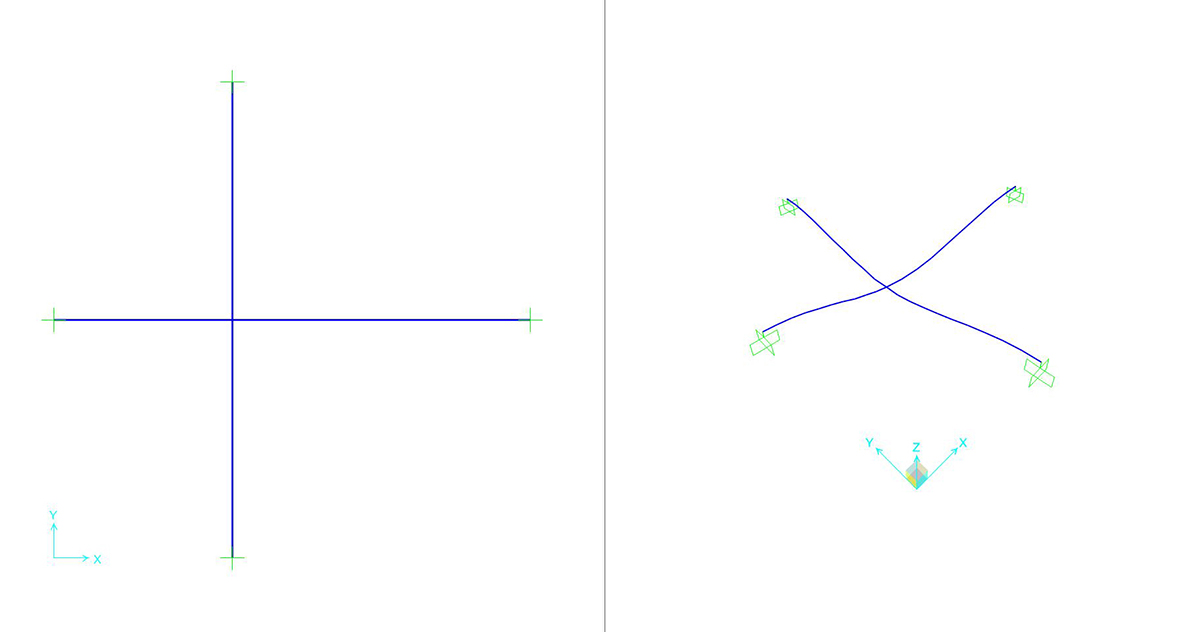
Possiamo ora avviare l’analisi. Il software mostra per prima cosa l’andamento della deformata.

 

 

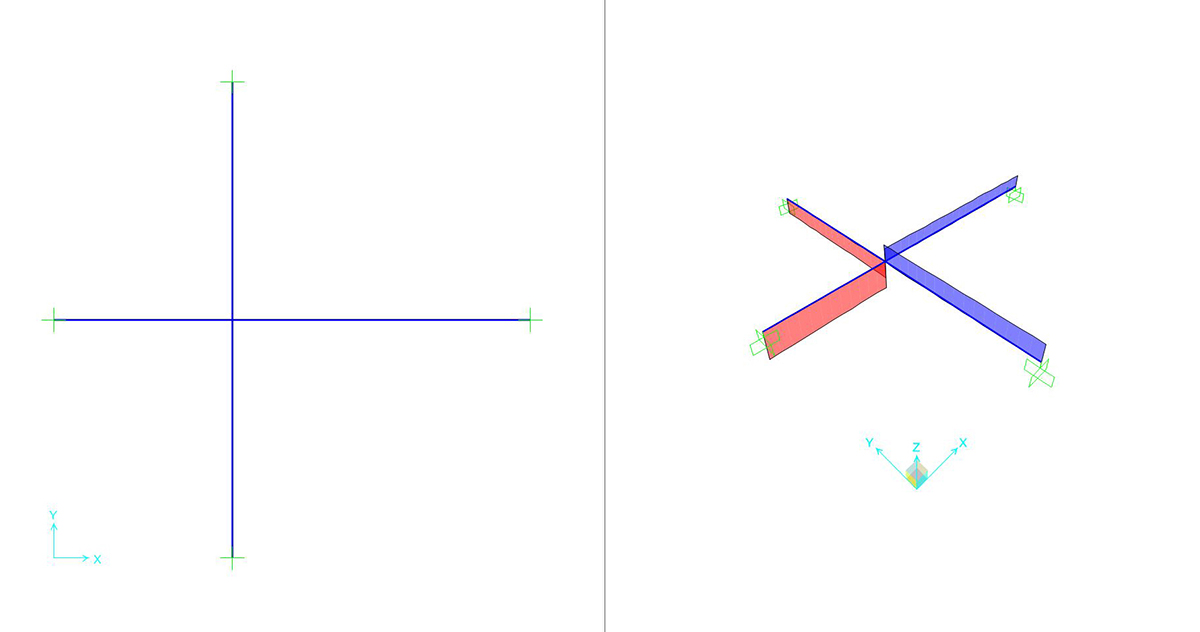
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > SHEAR 22

 

 

Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > MOMENT 33

 

 

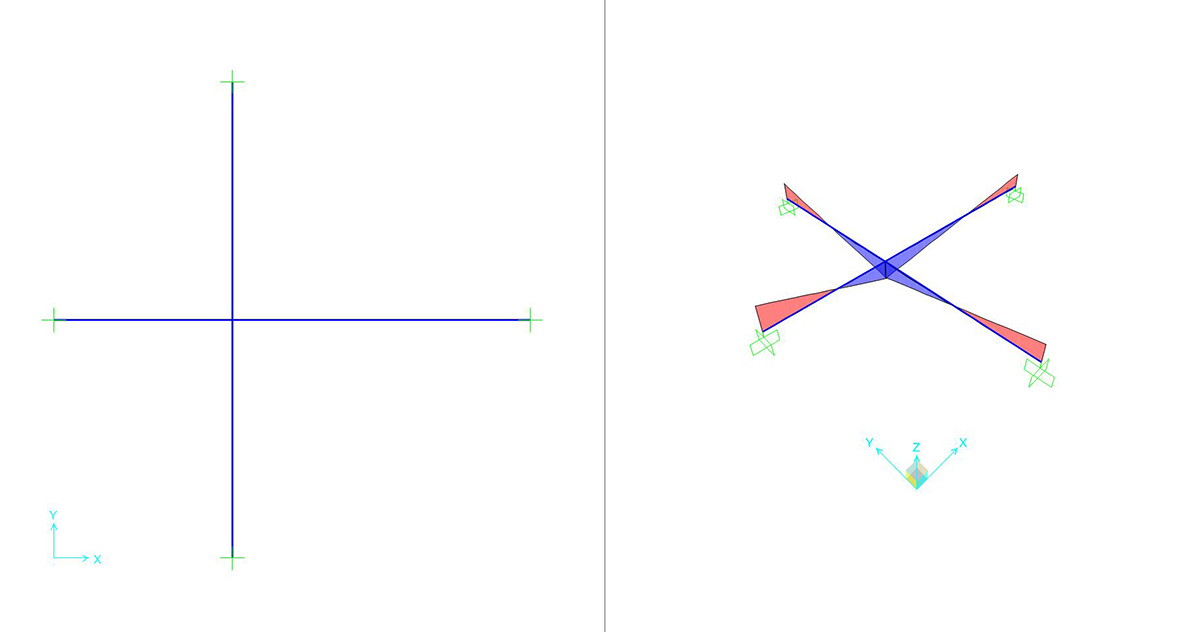
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION

 

 

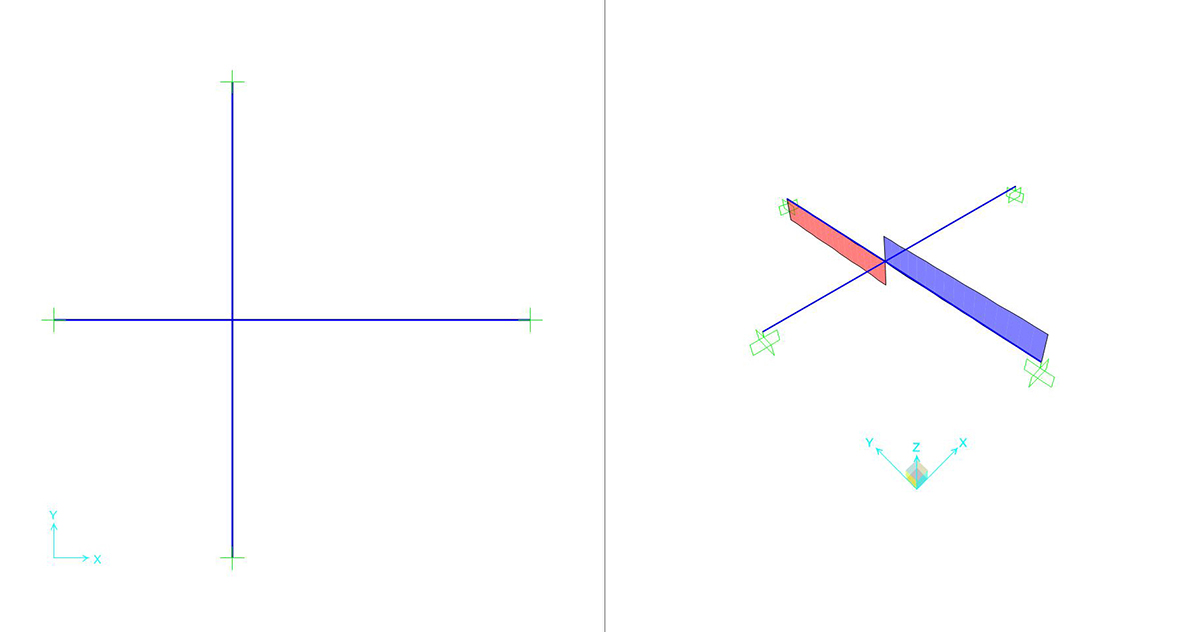
Possiamo ora avviare l’analisi della struttura in funzione delle varie sezioni assegnate.

 

ACCIAIO

SEZIONE QUADRATA CAVA

 

 

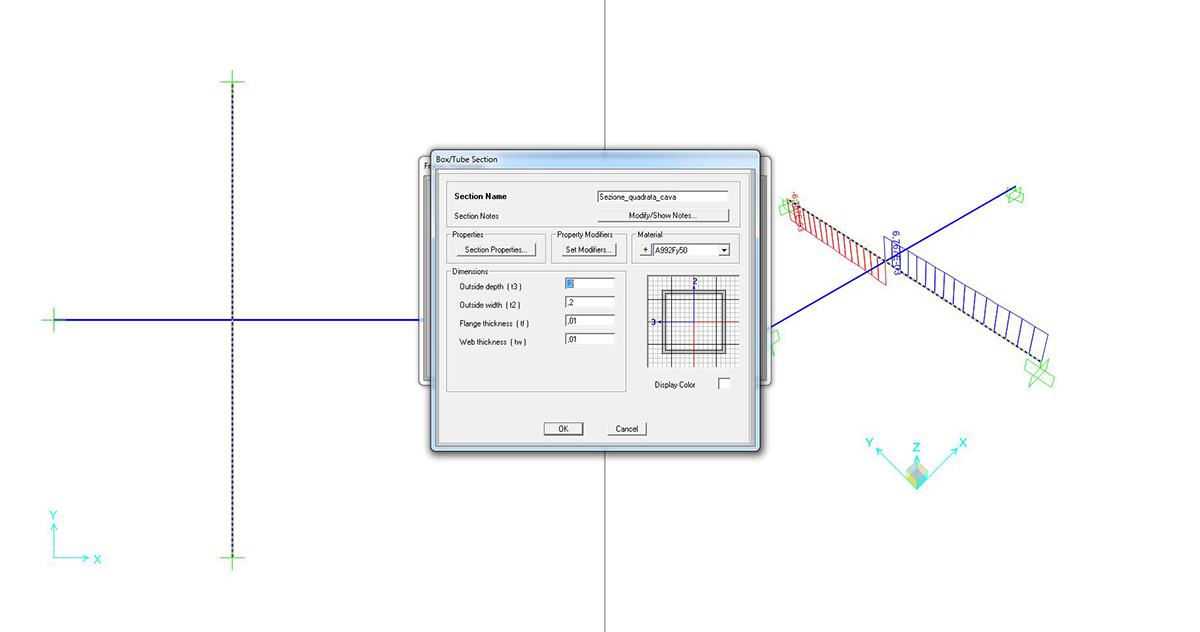
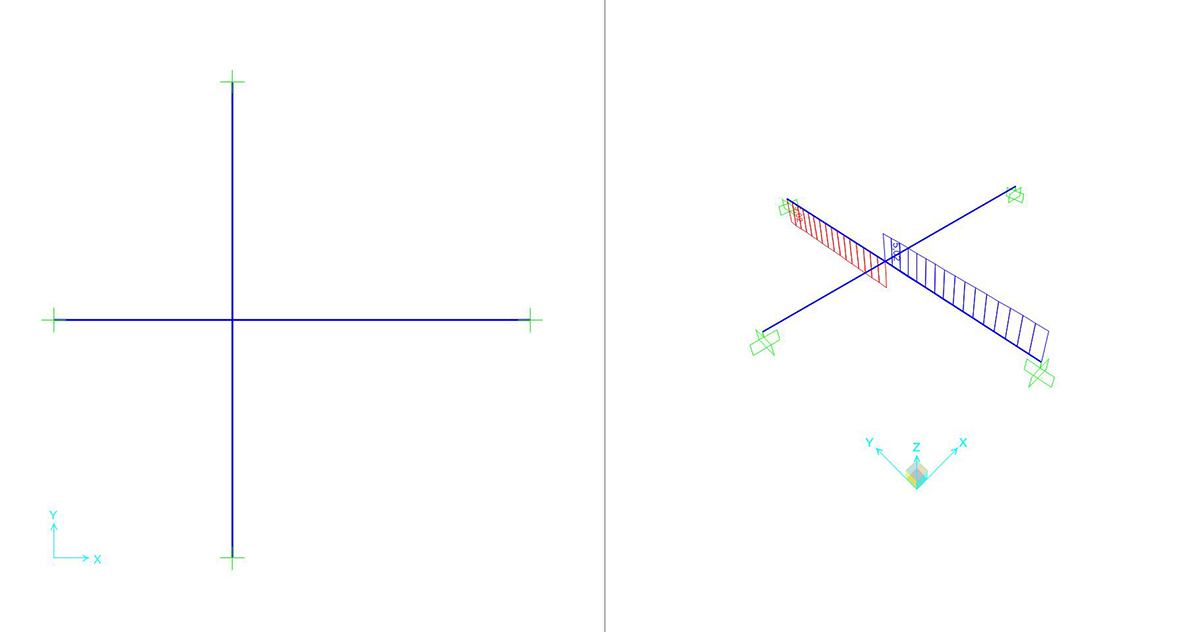
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION

 

 

HEA 200

 

 

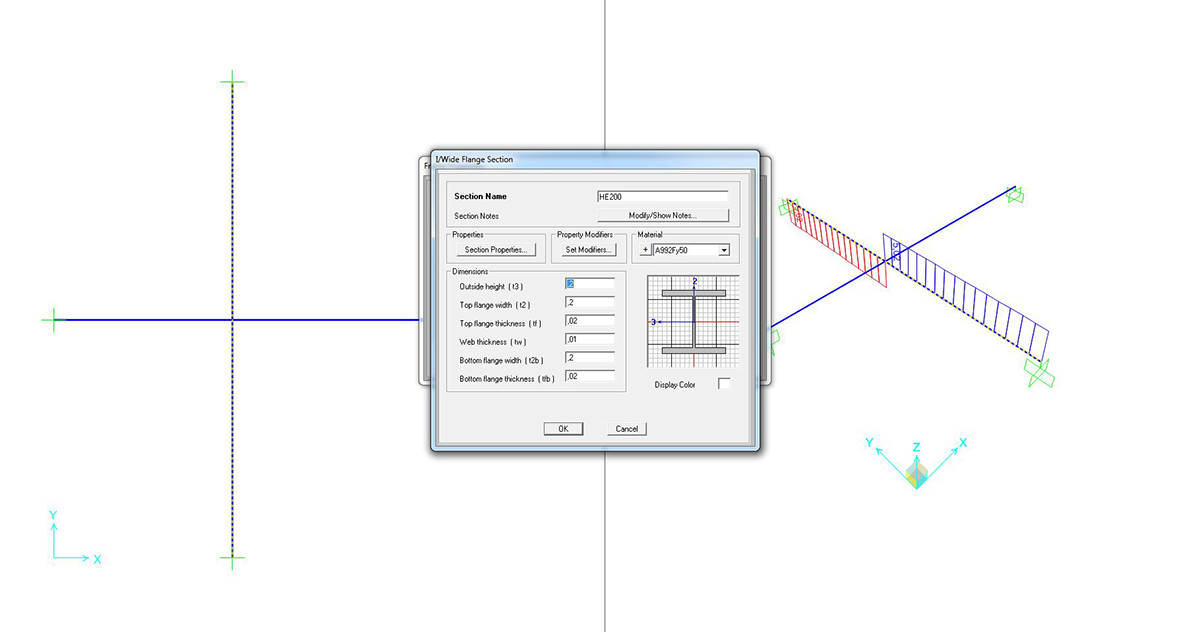
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION

 

 

SEZIONE CIRCOLARE CAVA

 

 

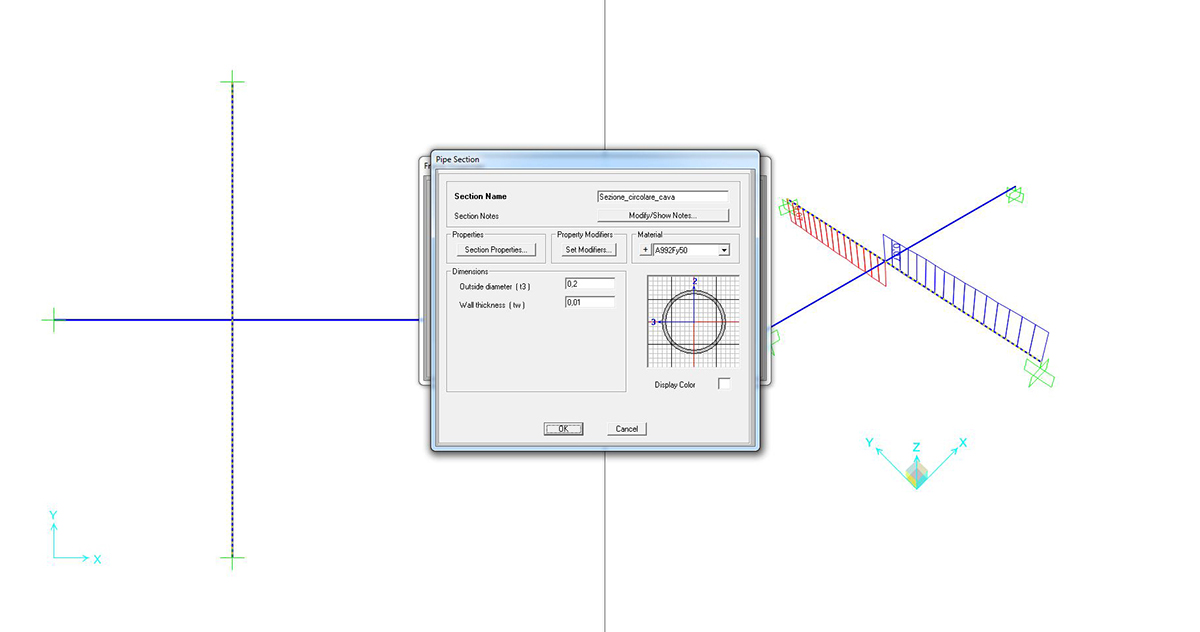
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION

 

 

CA

SEZIONE RETTANGOLARE 15cm_67cm

 

 

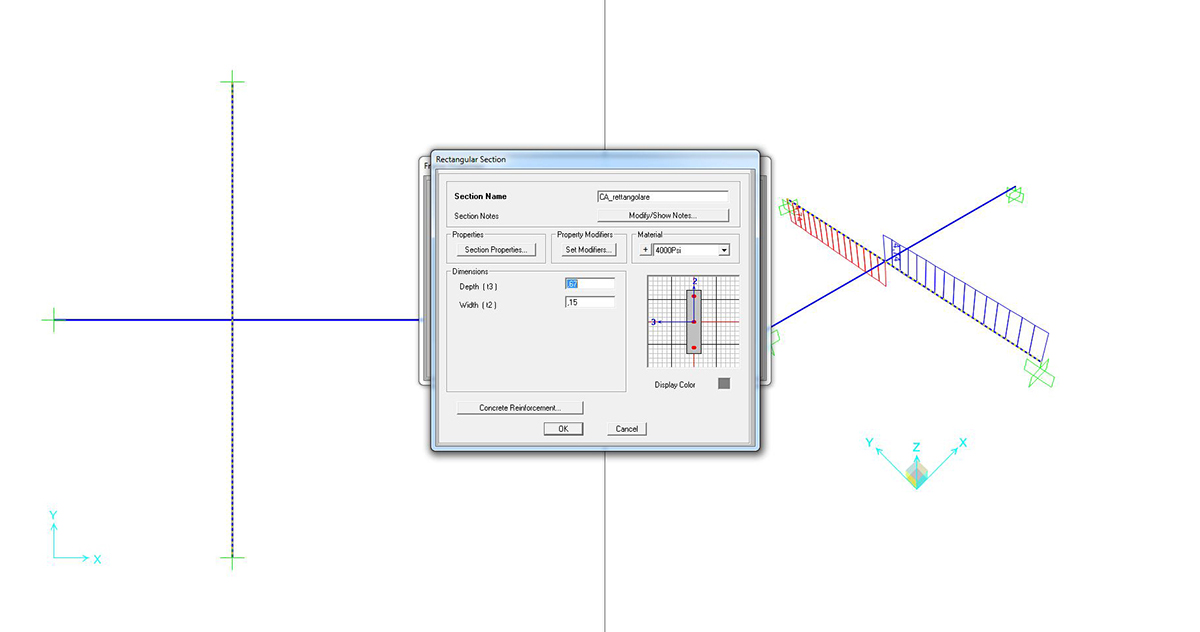
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION

 

 

SEZIONE CIRCOLARE 36cm

 

 

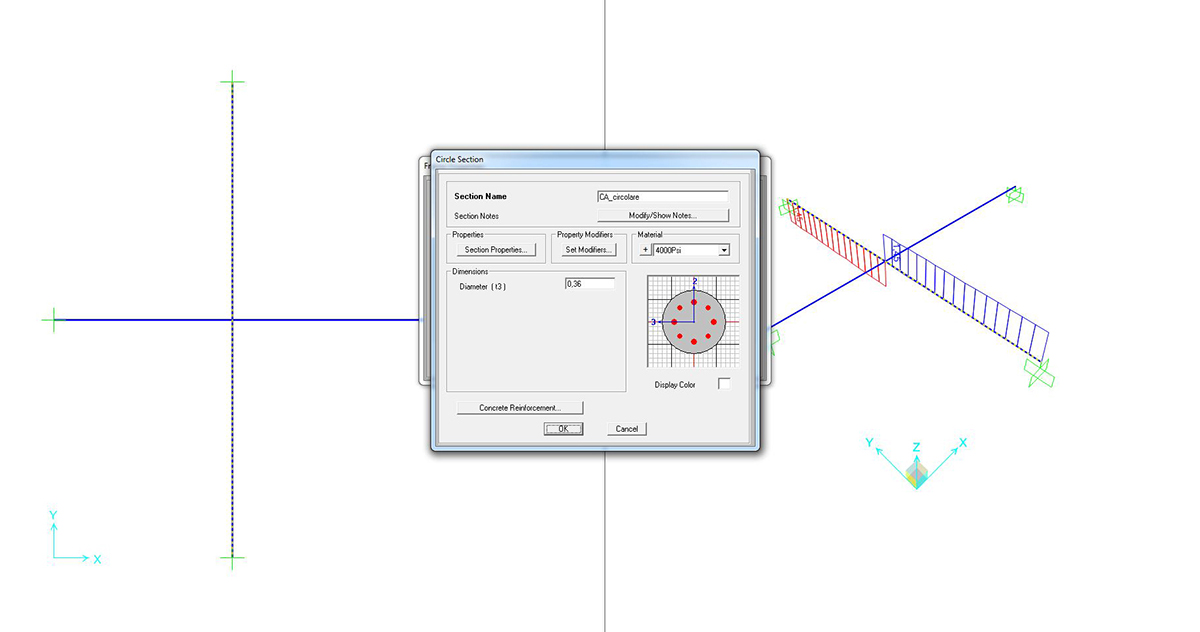
Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > TORSION