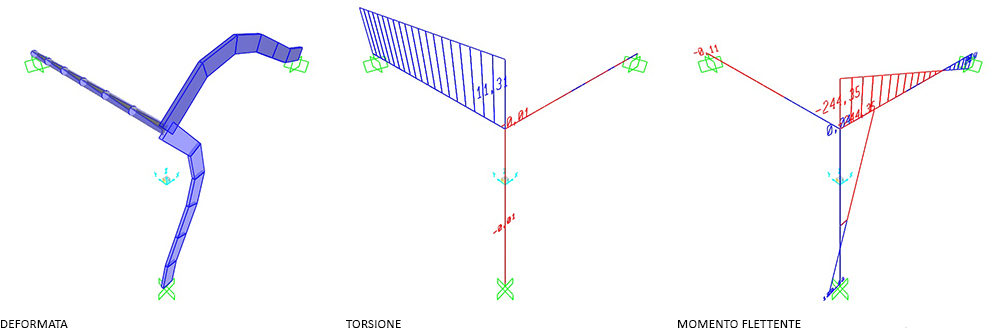
ESERCITAZIONE 7_RIGIDEZZA TORSIONALE

Si tratta di un nodo tridimensionale in C.A., materiale che assicura l'omogeneità.

La struttura è 12 volte iperstatica, perchè per ogni incastro tridimensionale ha 6 gradi di vincolo per un totale di 18 gradi di vincolo, ma ha anche 6 gradi di libertà, 18 - 6 = 12

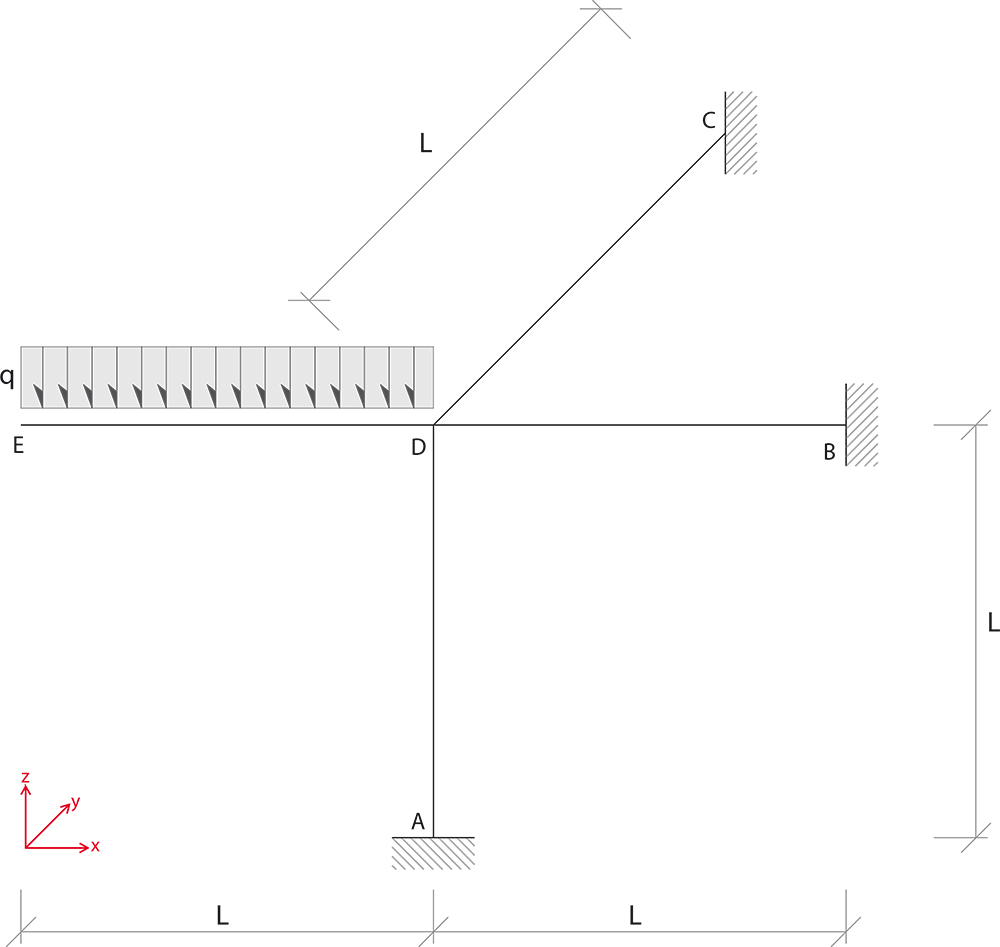
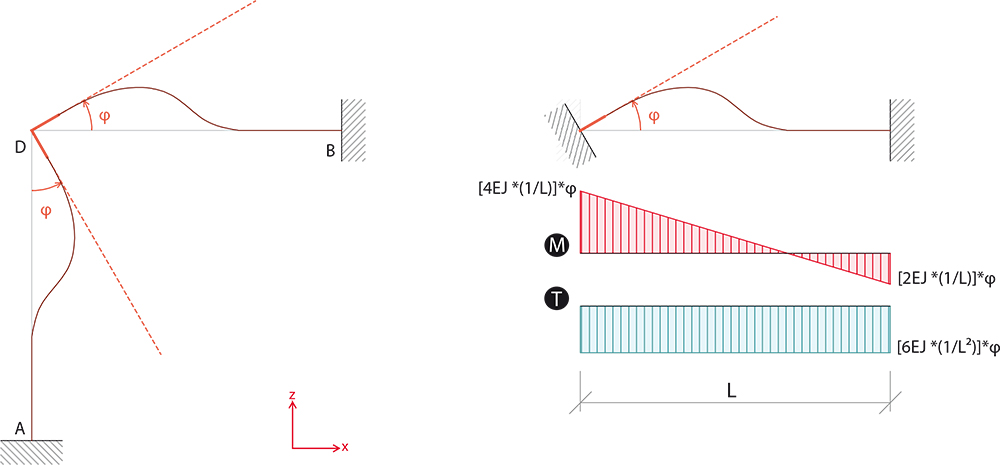
Lavoreremo solotanto sul piano XZ trascurando l'asta EC appartenente al piano YZ. Consideriamo l' asta ED ( mensola con carico ripartito quindi isostatica) separata dal resto della struttura, e ne studiamo Momento e Taglio per applicarli al nodo D:

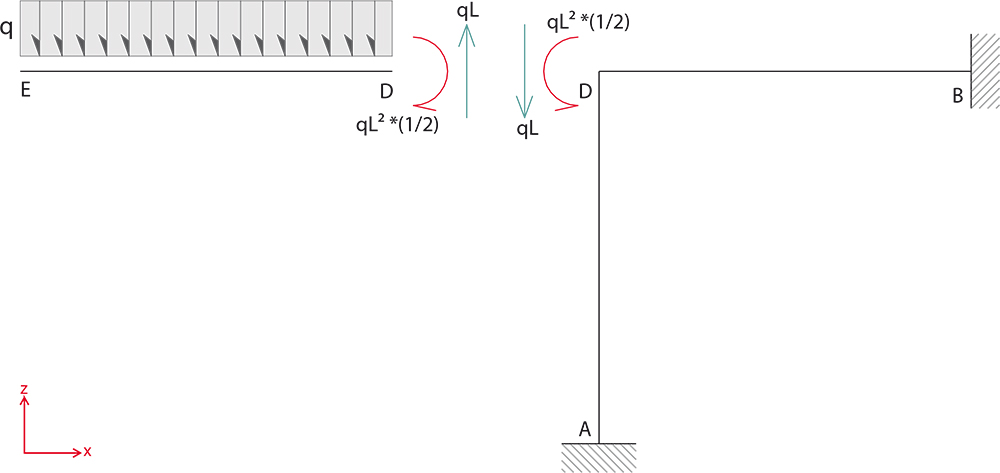
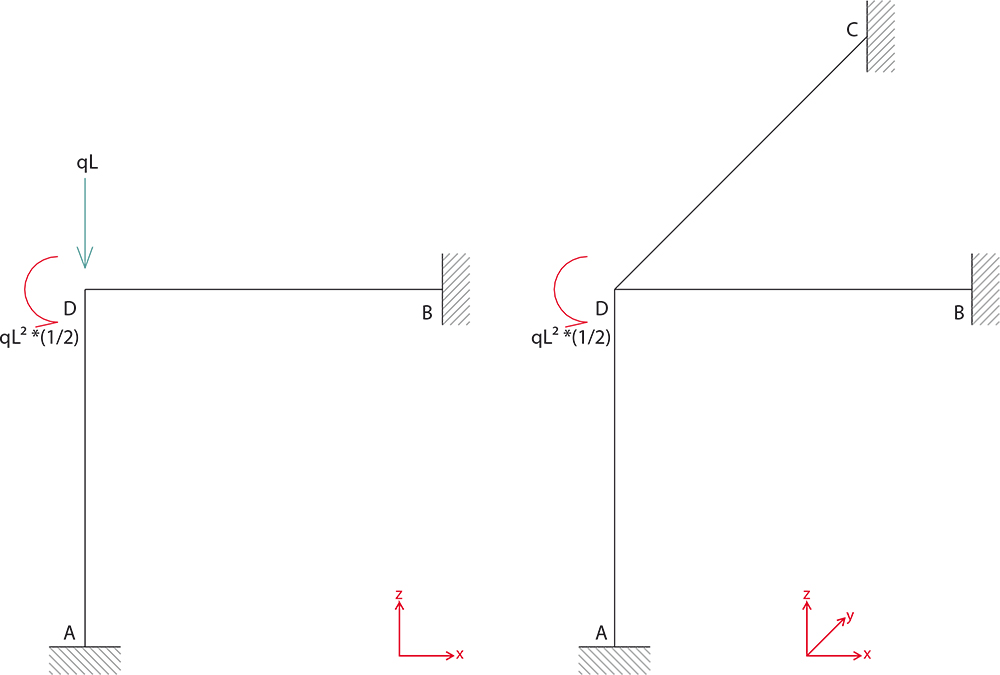
Essendo qL in asse con il pilastro, e considerando la rigidezza assiale molto più grande di quella flessionale, non la consideriamo.

Sul piano XZ il momento flettente (qL²)/2  provova una rotazione dell'asta DB e DA e genera un momento torcente sull' asta DC, perpendicolare al piano dove  agisce il momento flettente, che vale: 

Rt*φ

dove Rt è la rigidezza torsionale e vale

Rt = (GJt)/L

dove G è il modulo di elasticità tangenziale, ed è una caratteristica del materiale

G = τ/γ

e Jt è il momento d'inerzia torsionale

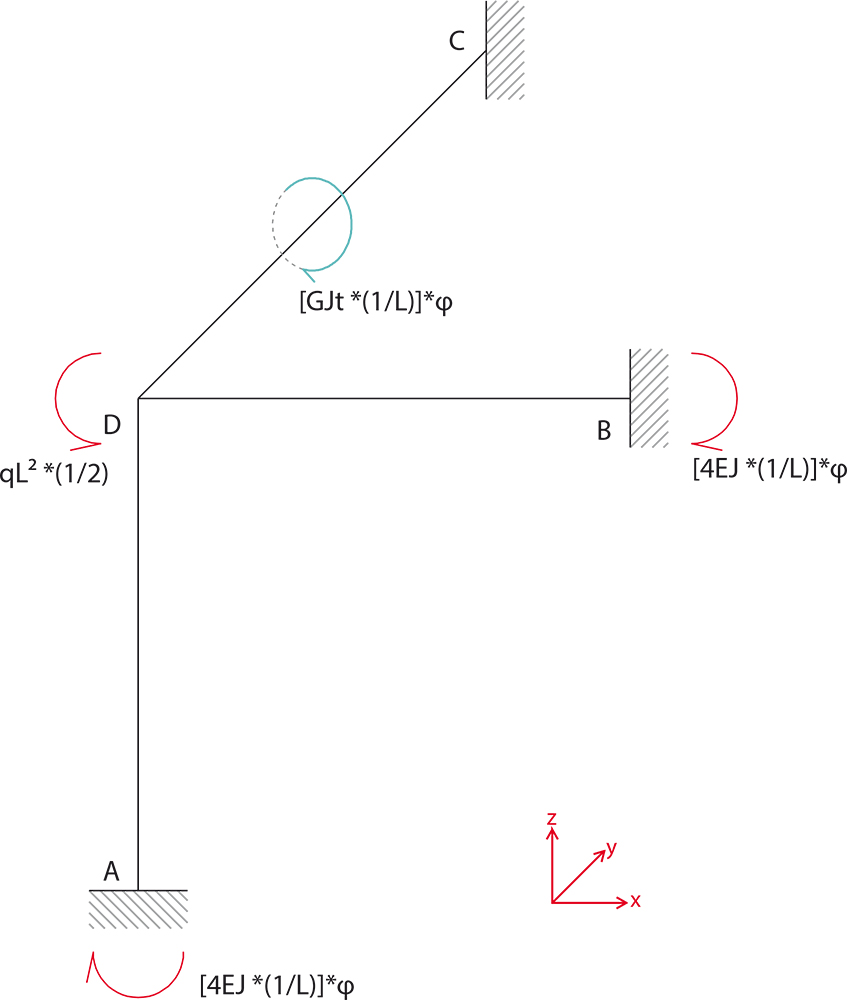
Facciamo la verifica al nodo D della struttura 3D considerando tutti i momenti:

(qL²)/2- [(4EJ)/L]*φ - [(4EJ)/L]*φ - [(GJt)/L]*φ =0 -> (qL²)/2 = φ([(4EJ)/L] + [(4EJ)/L] + [(GJt)/L]) -> 

φ = [(qL²)/2] * (1/K) dove ([(4EJ)/L] + [(4EJ)/L] + [(GJt)/L]) = K (rigidezza del nodo)

sostituendo il valore della rotazine nel momento flettente e nel momento torcente si ha:

Mf = (2EIql)/K

Mt = (GJtql)/2k

Considerando diverse sezioni per la struttura, i valori dei due momenti ( flettente e torcente) varieranno al variare del materiale (acciao e cls ) e della geometria della sezione:

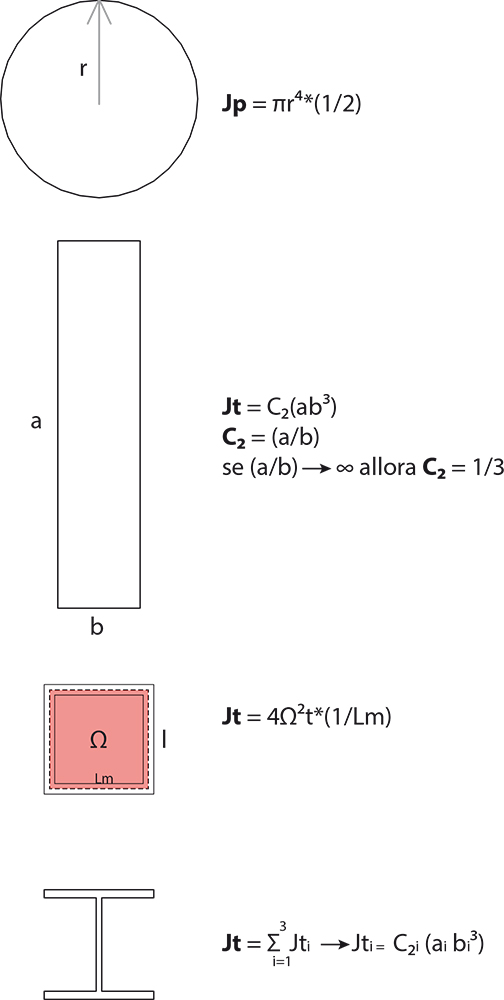
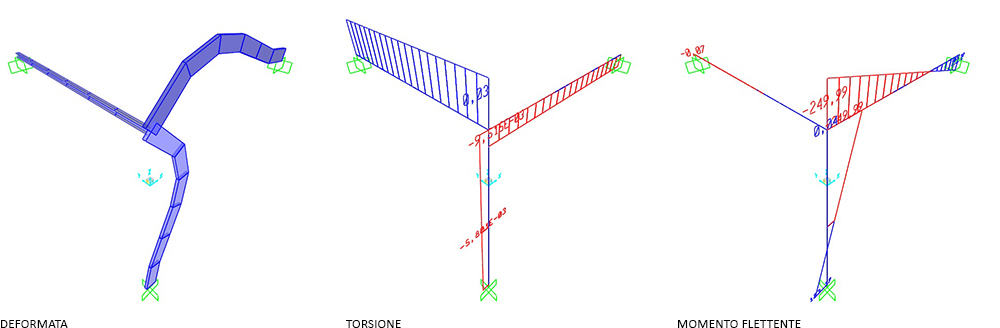
VERIFICA SU SAP:

SEZIONE HE 

b = 20 cm 

h = 20 cm

tw = 1 cm

tf = 1,5 cm

SCATOLARE QUADRATO

l = 20 cm 

t = 1 cm

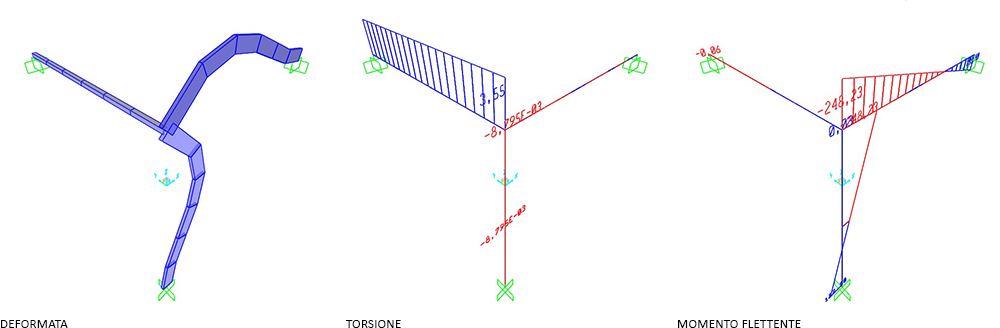
SEZIONE RETTANGOLARE (cls)

a = 67 cm

b = 15 cm

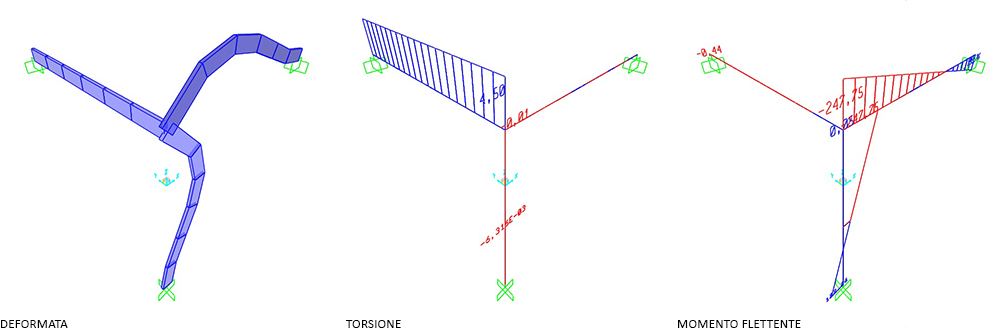
SEZIONE CIRCOLARE (cls)

r  = 18 cm