blog di Giacomo.Gasbarri

Si tratta di un nodo tridimensionale in C.A., materiale che assicura l'omogeneità.

La struttura è 12 volte iperstatica, perchè per ogni incastro tridimensionale ha 6 gradi di vincolo per un totale di 18 gradi di vincolo, ma ha anche 6 gradi di libertà, 18 - 6 = 12

Lavoreremo solotanto sul piano XZ trascurando l'asta EC appartenente al piano YZ. Consideriamo l' asta ED ( mensola con carico ripartito quindi isostatica) separata dal resto della struttura, e ne studiamo Momento e Taglio per applicarli al nodo D:

Essendo qL in asse con il pilastro, e considerando la rigidezza assiale molto più grande di quella flessionale, non la consideriamo.

Sul piano XZ il momento flettente (qL²)/2  provova una rotazione dell'asta DB e DA e genera un momento torcente sull' asta DC, perpendicolare al piano dove  agisce il momento flettente, che vale: 

Rt*φ

dove Rt è la rigidezza torsionale e vale

Rt = (GJt)/L

dove G è il modulo di elasticità tangenziale, ed è una caratteristica del materiale

G = τ/γ

e Jt è il momento d'inerzia torsionale

Facciamo la verifica al nodo D della struttura 3D considerando tutti i momenti:

(qL²)/2- [(4EJ)/L]*φ - [(4EJ)/L]*φ - [(GJt)/L]*φ =0 -> (qL²)/2 = φ([(4EJ)/L] + [(4EJ)/L] + [(GJt)/L]) -> 

φ = [(qL²)/2] * (1/K) dove ([(4EJ)/L] + [(4EJ)/L] + [(GJt)/L]) = K (rigidezza del nodo)

sostituendo il valore della rotazine nel momento flettente e nel momento torcente si ha:

Mf = (2EIql)/K

Mt = (GJtql)/2k

Considerando diverse sezioni per la struttura, i valori dei due momenti ( flettente e torcente) varieranno al variare del materiale (acciao e cls ) e della geometria della sezione:

VERIFICA SU SAP:

SEZIONE HE 

b = 20 cm 

h = 20 cm

tw = 1 cm

tf = 1,5 cm

SCATOLARE QUADRATO

l = 20 cm 

t = 1 cm

SEZIONE RETTANGOLARE (cls)

a = 67 cm

b = 15 cm

SEZIONE CIRCOLARE (cls)

r  = 18 cm

Definiamo un impalcato composto da 4 telai piani lungo l' asse X e 3 lungo l' asse Y, e un totale di  10 pilastri che dovranno assorbire, oltre ai carichi verticali, le forze orizzontali sul piano xy;

con pilastro in C.A. a sezione rettangolare:

con un Momento d' Inerzia pari a J = (bh³)/12

Coordinate del CENTRO DI MASSA (G) -> Il calcolo per l' impalcato studiato consiste  nella semplificazione della planimetria in geometrie più semplici delle quali troviamo le coordinate dei rispettivi centri

Coordinate del CENTRO DELLE RIGIDEZZE (C) -> Il punto dove si concentrano le risultanti delle resistenze orizzontali

Una trave Vierendeel non è altro che un telaio shear-type ruotato di 90° su un fianco.

Un telaio shear-type è un impalcato con due fondamentali ipotesi:

_La trave è infinitamente resistente a flessione

_I pilastri non si deformano  se sottoposti ad un qualsiasi sforzo normale

Questo tipo di telaio assume come rigidezza totale la somma di tutte le rigidezze dei suoi pilastri.

                                                                                                             F = Kδ * δ -> δ = F / Kδ

In questo caso sono i pilastri ad essere infinitamente resistenti a flessione e le travi non deformabili a sforzo normale.

Possiamo considerare i traversi come delle travi doppiamente incastrate che subiscono un cedimento vincolare verticale uguale a delta
causato da una forza puntuale F, il taglio sarà costante e il momento Lineare, e il punto di flesso corrisponde al punto dove il momento si annulla

Lo scopo dell' esercizio è tovare:

1-> Taglio sulle travi;
2-> Momento sulle travi;
3-> Momento sui pilastri;
4-> Taglio sui pilastri;
5-> Valori di δ1, δ2, δ3;

Il valore dello sforzo di Taglio nella trave viene ricavato dall'integrazione della linea elastica:

T = 12EIδ/(L³)

dalla formula del taglio ricaviamo il valore dello spostamento δ

Sfruttando la simmetria della trave, può esserne studiata una sola metà:

1-> Taglio sulle travi-> La forza che agisce sulla trave viene ripartita ugualmente sui due traversi, inferiore e superiore:

2-> Momento sulle travi-> Per calcolare il Momento sulle travi moltiplico ogni taglio per il suo braccio (L/2),

        M = T*(L/2)

3-> Momento sulli pilastri-> Per calcolare il momento nei pilastri dobiamo studiare il nodo e trovare dei momenti che equilibrino quelli agenti sulle travi:

4-> Taglio sulli pilastri-> M = T*b -> T = M/b

5-> Valori di δ1, δ2, δ3 -> Dopo aver equilibrato tutto possiamo andare a calcolare i valori degli spostamenti:

T₁ = 12EIδ₁/(L³) -> δ_{1 =} FL³/(48EI)

                                 -> δ_{2 =} FL³/(16EI)

                                 -> δ₃₌ FL³/(48EI)

Il metodo delle Forze consente di risolvere strutture iperstatiche come travi o travi continue su più appoggi, riconducendole a strutture isostatiche di riferimento delle quali sono noti spostamenti e rotazioni, e ponendo come incognite le reazioni vincolari iperstatiche in modo da ristabilire la compatibilità cinematica dei vincoli soppressi.

Risoluzione di una Trave su appoggi, 3 volte iperstatica, con il metodo delle forze.

Svincolo le cerniere in B, C, D, rendendole cerniere passanti, e applico tre momenti incogniti X1, X2, X3.

Dobbiamo applicare il principio della sovrapposizione per calcolare gli effetti dovuti al carico q e dai momenti applicati X:

Dovendo ritornare ad una condizione di iperstaticità,

e riordando i valori delle rotazioni dovute al carico ripartito q (pl³/24EI)e le rotazioni Primarie (XL/3EI) e Secondarie (XL/6EI) dovute ai momenti incogniti applicati,

poniamo le rotazioni in ogni carrello uguale a zero, scriviamo queindi le EQUAZIONI DI CONGRUENZA per ogni punto (B, C, D)

mettendo a sistema i valori delle rotazioni in B e C (con B = D), ricavo i valori dei momenti applicati.

Ora studiamo le reazioni sulla trave, suddivisa in 4 tratti, dovuti al carico ripartito q:

e ai momenti assegnati: X1 e X3

e X2

e ottengo le reazioni, i valori degli sforzi di Taglio e Momento Flettente che il carico e i momenti producono sulla trave iperstatica:

Verifica su Sap degli sforzi calcolati:

Taglio

Momento

SOLAIO IN LEGNO: Dimensionamento trave in legno Lamellare

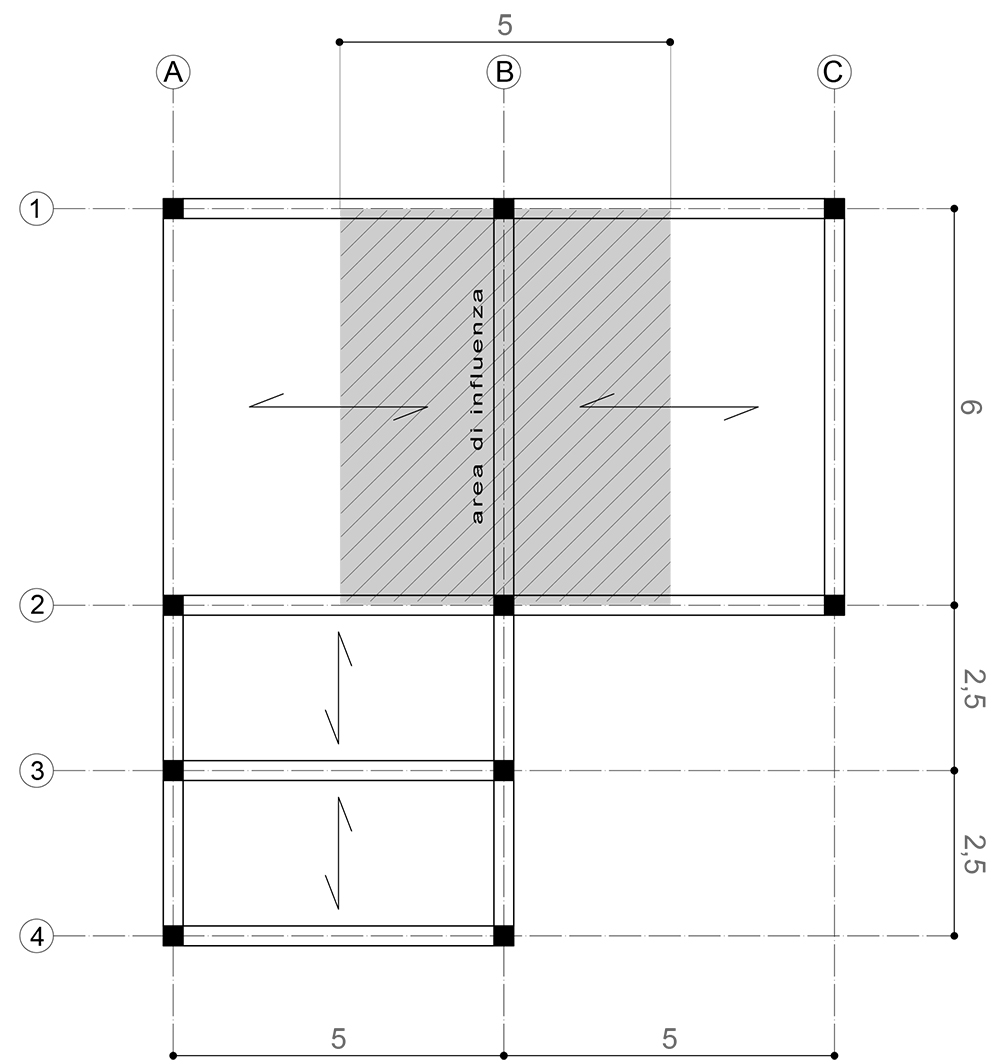
Trave B (1- 2)

luce = 6 m

interasse = 5 m

area di influenza =30 mq (5x6 m)

Definizione destinazione d'uso

Categoria A ( ambienti ad uso residenziale)

Definizione dei carichi:

Carichi strutturali (qs)= travi, travetti, tavolato

Carichi permanenti (qp)= pavimento in parquet, massetto, isolante acustico, impianti, tramezzi

Carichi accidentali (qa) = 2 N/mmq( tabellati secondo normativa)

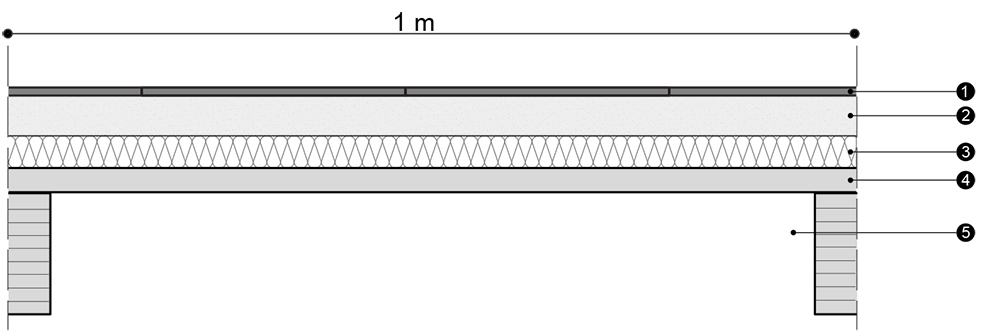
1) Pavimento in Parquet di Rovere (spessore: 1 cm)

2) Massetto alleggerito (spessore 5 cm)

3) Isolamento acustico in fibra di legno (spessore 4 cm)

4) Tavolato in legno di Rovere(spessore: 3 cm)

5) Travetto in legno lamellare

Calcolo qs:

Tavolato in legno di Rovere(spessore: 3 cm):

Peso Specifico = 6.9 KN/mc

Volume al mq =  0.03 m x 1 m x 1 m = 0.03 mc

Peso al mq = 0.03 m x 6.9 KN/mc = 0.207 KN/mq

Travetti in legno lamellare(classe di resistenza GL24h; dim.: 15x10 cm)

Peso Specifico = 3.73 KN/mc

Volume  =  (0.15 x 0.10) m x 1m x 1m = 0.015 mc

Peso al mq = 0.015 m x 3.73 KN/mc = 0.056 KN/mq

qs = 0.263 KN/mq

Calcolo qp:

Pavimento in Parquet di Rovere (spessore: 1 cm):

Peso Specifico = 7.06 KN/mc

Volume al mq =  0.01 m x 1m x 1m = 0.01 mc

Peso al mq = 0.01 mc x 7.06 KN/mc = 0.0706 KN/mq

Massetto alleggerito (spessore 5 cm):

Peso Specifico = 4.71 KN/mc

Volume  al mq =  0.05 m x 1m x 1m = 0.05 mc

Peso al mq = 0.05 mc x 4.71 KN/mc = 0.236 KN/mq

Isolamento acustico in fibra di legno (spessore 4 cm):

Peso Specifico = 2.11 KN/mc

Volume  al mq =  0.04 m x 1m x 1m = 0.04 mc

Peso al mq = 0.04 mc x 2.11 KN/mc = 0.084 KN/mq

Incidenza Impianti:

0.5 KN/mq

Incidenza Tramezzi:

1 KN/mq

qp = 1.891 KN/mq

Carico Totale:

(qa + qs + qp) x interasse = (0.2 + 0.263 + 1.891) KN/mq  x 5 m =11.77 KN/ml

K,mod = 0.6( tabellato per i legni lamellari e corrisponde)

Per Legno Lamellare(classe di resistenzaGL24h)

fm,k = 24 Mpa (resistenza a flessione)

ρk = 3.73 KN/mc (massa volumica)

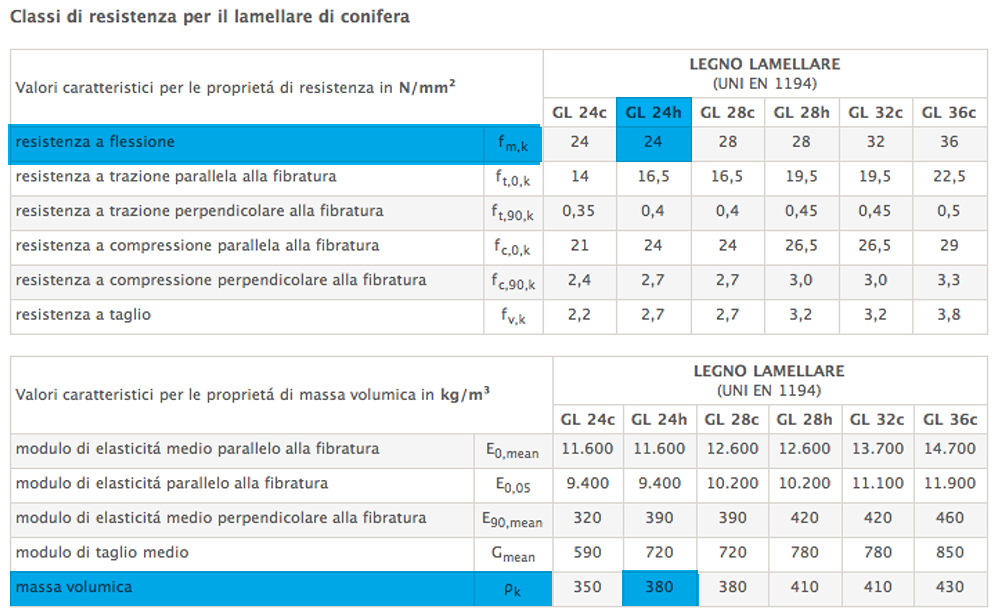
Dal calcolo finale ottengo un altezza minima di 43,40 cm, 

TRAVE' : 30 x 45 cm

Verifica:

Per effettuare la verifica devo sommare al qs iniziale il peso relativo alla trave:

Travetti in legno lamellare(classe di resistenza GL24h; dim.: 30x45 cm)

Peso Specifico = 3.73 KN/mc

Volume  trave =  0.30 m x 0.45 m x 6 m = 0.81 mc

Peso trave = 0.81 mc x 3.73 KN/mc = 3.02 KN/mq

qs = ( 0.263 + 3.02 ) KN/mq = 3.284 KN/mq

Poiché ottengo un altezza minima di 52.79 cm  > 45 cm dovrò considerare una trave con sezione maggiore:

TRAVE'':  30x55 cm

oppure per ridurre l'altezza della trave senza fare riferimento ad una categoria resistente diversa di legno lamellare con peso e resistenza maggiore aumento le dimensioni della base diminuendo l'altezza

TRAVE''': 40x50 cm

#1_TRAVE RETICOLARE 3D(SAP)

Dopo aver disegnato una struttura reticolare in 3 dimensioni, avente modulo quadrato L x L, con L = 2 m, viene immessa nella in SAP, avendo l'accortezza di separare ogni singola ASTA dalle altre ed aver approssimato  l'errore nei nodi con uno scarto più basso possibile.

Si assegnano i tre vincoli in modo che non siano allineati:

Si definisce una sezione per le ASTE, in questo caso una sezione scatolare cilindrica d'acciaio di spessore 4 mm e diametro 15 mm:

s = 4 mm

d = 15 mm

Si assegnano le Forze puntuali di 40 KN su ogni nodo superiore della struttura e rilascia tutta la struttura dal momento e si elimina il perso proprio della struttura dall'equazione:

Una volta avviata l' analisi della struttura se ne ricavano i diagrammi della struttura DEFORMATA, e delle sollecitazioni di COMPRESSIONE e TRAZIONE in ogni asta

e i valori della TENSIONE interna alle aste:

#2_TRAVE RETICOLARE 2D (SAP+RITTER/NODI)

Una travatura reticolare si riconosce semplicemente se le aste hanno solo sforzo normale N di trazione (+) o compressione (-), ed è isostatica in quando è formata da triangoli.

La struttura reticola isostatica è simmetrica, quindi possiamo studiarne una metà, ne numeriamo i nodi e procediamo con lo studio degli sforzi normali all'interno di ogni asta:

N_9,7*L+F*L+F*2L+F*3L+F*4L-F*(9/2)*4L=0 -> N_9,7=8F

N_8,10*L+F*L+F*2L+F*3L-F*(9/2)*3L=0 -> N_10,8=F*(15/2)

N_7,10(√2/2)-N_9,7+N_{8,10=0 ->} N_7,10=F*(1/√2)

N_10,8=F*(15/2)

N_7,5*L+F*L+F*2L+F*3L-F*(9/2)*3L=0 ->N_7,5=F*(15/2)

-N_7,8-F-F-F+F*(9/2)=0 -> N_7,8=F*(3/2)

N_7,5=F*(15/2)

N6,8*L+F*L+F*2L-F*(9/2)*2L=0 ->N_6,8=6F

N_5,8(√2/2)-N_7,5+N_6,8=0->N_5,8=F*(3/√2)

N_5,3=6F

 

N_4,6*L+F*L-F*(9/2)*L=0 ->N_4,6=F*(7/2)

 

N_3,6(√2/2)-6F+F*(7/2)=0 ->N_3,6=F*(5/√2)

 

N_6,4=F*(7/2)

 

N_3,2*L+F*L-F*(9/2)*L=0 ->N_3,2=F*(7/2)

 

-N_3,4-F+F*(9/2)=0 ->N_3,4=F*(7/2)

N3,2=F*(7/2)

 

N1,4=0 

 

N2,4(√2/2)-F*(7/2)=0 ->N2,4=F*(7/√2)

 

N_3,2=F*(7/2)

 

N_1,4=0 

 

N_2,4(√2/2)-F*(7/2)=0 ->N_2,4=F*(7/√2)

 

N_1,2=F*(9/2)

 

Gli sforzi sulla trave sono:

                               

indicando in Blu i puntoni (compressi) e in Rosso i tiranti (tesi).

 

VERIFICA SU SAP

Imposto la trave reticolare in SAP con

L=2 m

F=10 KN

e una sezione cilindrica cava per le aste

                     

Sforzi assiali:

                    

Deformata:              

                     

 

N6,4=F*(7/2)

 

N4,6*L+F*L-F*(9/2)*L=0 ->N4,6=F*(7/2)

 

-N3,4-F+F*(9/2)=0 ->N3,4=F*(7/2)

01_Definisco una trave di lunghezza L=2m utilizzando una griglia:
       File -> New Model -> Grid Only

02_Dopo aver disegnato la trave, assegno i vincoli ai due estremi:
       seleziona punto -> Assign-> Joint -> Restraints

03_Definisco la sezione della trave con uno scatolare rettangolare d’ acciaio (100x300) mm:
       seleziona tutto -> Define -> Section Properties -> Frame section -> Add new proprerty -> Steel -> Section name
       (per distinguere i componenti delle strutture) -> imposto dimensioni e spessori

04_Togliere il peso proprio della struttura:
       Define -> Load patterns -> Self weight multiplier = 0 (per eliminare il peso proprio della struttura
       dall’ equazione) -> Add new load patterns

05_Definisco il carico uniformemente distribuito sulla trave q = 40 KN/m
       Assing -> Frame Loads (è per i carichi) -> Distribute

06 _Ora, conoscendo il significato geometrico della derivata, sappiamo che dove la retta tangente alla curvatura è orizzontale all'asse delle x, la derivata è nulla;

φ_(s) = 0

Ciò accadra nei punti di massimo (o minimo) della deformata della trave. Sapendo inoltre che la derivata prima dello spostamento:

v_(s)= φ_(s) = (dv/ds)= [-q/(EJ)*(s³/6)]+[C₁*(s²/2)]+[C₂*s] = 0

e avendo calcolato le costanti di integrazione in relazione con le condizioni al bordo (vincoli della trave: incastro e carrello):

C₄= 0, C₃= 0, C₂= -1/8*[(ql²)/(EJ)] , C₁= 5/8*[(ql/(EJ)] ; 

le sostituiamo nell'equazione della rotazione ponendola uguale a zero e risolvo rispetto s. Dopo aver trovato il punto corrispondente allo spostamento verticale massimo (v max), lo posiziono sulla trave con un offset dall’origine e inserendo le coordinate del punto calcolato ( x, y, z ), in questo modo potrò visualizzare in corrispondenza di tale punto il valore del TAGLIO, MOMENTO e SPOSTAMENTO VERTICALE (massimo). Dal calcolo analitico effettuato risulta:

                  s_{(v max)} = 0,578 L

Il punto appena trovato, corrisondente allo spostamento massimo della linea della trave, viene usato per calcolare il valore dello spostamento massimo stesso:

 v_max= [-q/(EJ)*(s⁴/24)]+[((ql)/(EJ))*(5/48)*s³]-[((ql²)/(EJ))*(1/16)*s²]

               v_max = -0.3307 mm (spostamento verticale verso il basso)

07_Inizio la verifica su SAP
       Play -> Run/Do not run all (per deselezionare tutto) -> selezionare il caso da calcolare definito nel punto 04 -> Run/Do not run case (per selezionare solo quel caso) -> Run Now  

                  Il valore dello spostamento verticale massimo calcolato su SAP è di  -0.4 mm, inerente con il risultato ottenuto analiticamene.