ESERCITAZIONE 5 _TRAVE VIERENDEEL_DOPPIAMENTE INCASTRATA

Una trave Vierendeel non è altro che un telaio shear-type ruotato di 90° su un fianco.

Un telaio shear-type è un impalcato con due fondamentali ipotesi:

_La trave è infinitamente resistente a flessione

_I pilastri non si deformano  se sottoposti ad un qualsiasi sforzo normale

Questo tipo di telaio assume come rigidezza totale la somma di tutte le rigidezze dei suoi pilastri.

                                                                                                             F = Kδ * δ -> δ = F / Kδ

In questo caso sono i pilastri ad essere infinitamente resistenti a flessione e le travi non deformabili a sforzo normale.

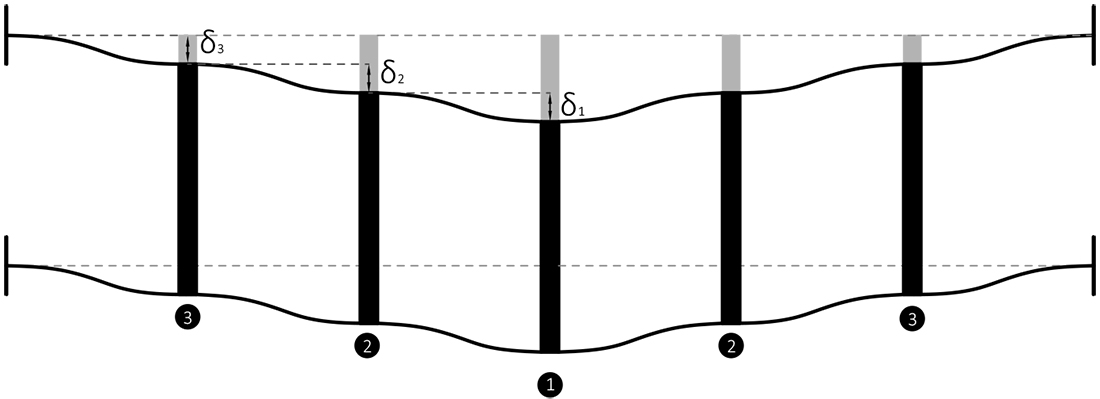
Possiamo considerare i traversi come delle travi doppiamente incastrate che subiscono un cedimento vincolare verticale uguale a delta
causato da una forza puntuale F, il taglio sarà costante e il momento Lineare, e il punto di flesso corrisponde al punto dove il momento si annulla

Lo scopo dell' esercizio è tovare:

1-> Taglio sulle travi;
2-> Momento sulle travi;
3-> Momento sui pilastri;
4-> Taglio sui pilastri;
5-> Valori di δ1, δ2, δ3;

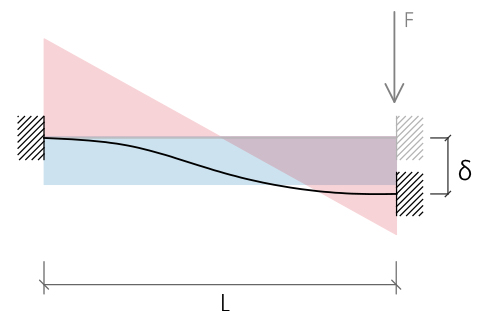
Il valore dello sforzo di Taglio nella trave viene ricavato dall'integrazione della linea elastica:

T = 12EIδ/(L³)

dalla formula del taglio ricaviamo il valore dello spostamento δ

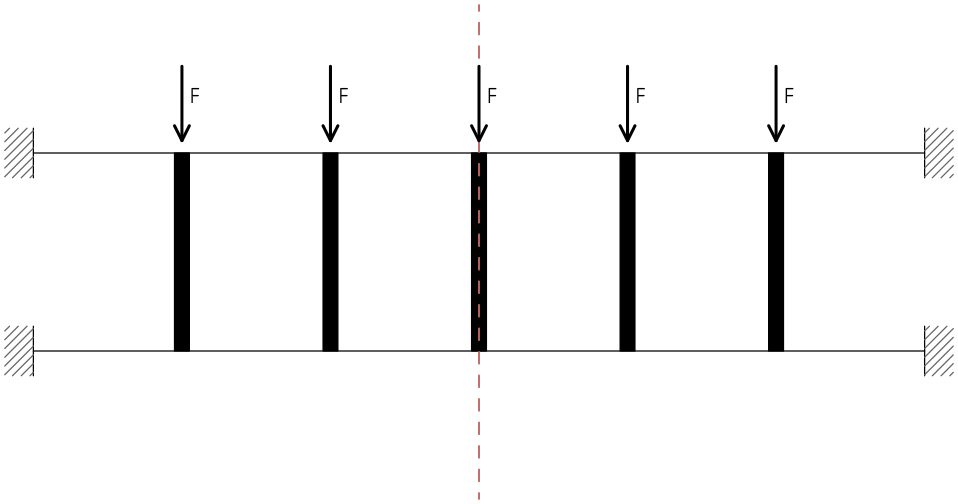
Sfruttando la simmetria della trave, può esserne studiata una sola metà:

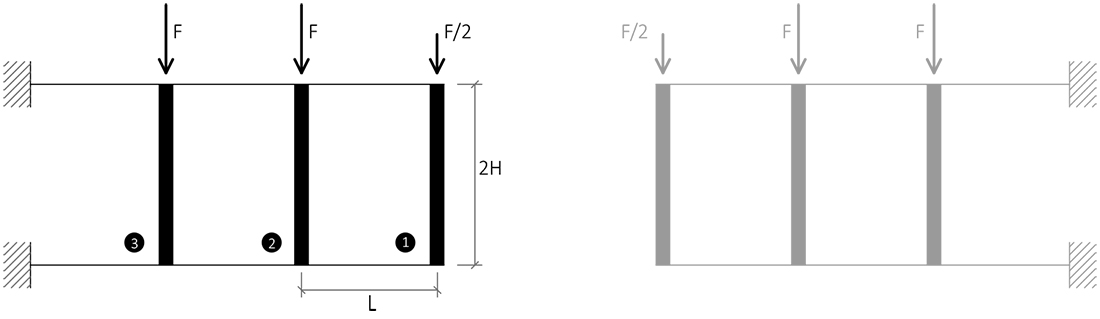
1-> Taglio sulle travi-> La forza che agisce sulla trave viene ripartita ugualmente sui due traversi, inferiore e superiore:

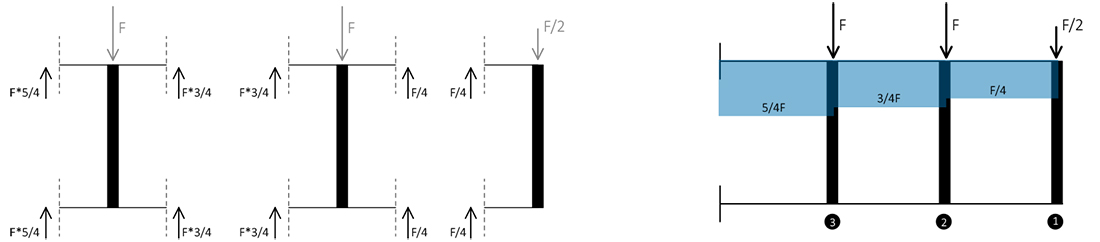
2-> Momento sulle travi-> Per calcolare il Momento sulle travi moltiplico ogni taglio per il suo braccio (L/2),

        M = T*(L/2)

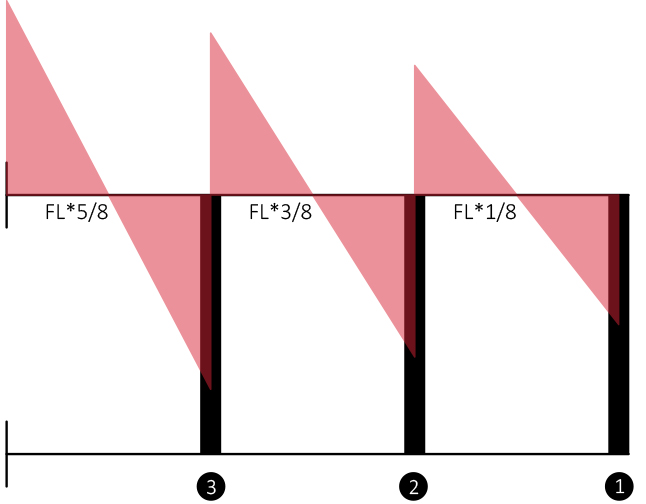
3-> Momento sulli pilastri-> Per calcolare il momento nei pilastri dobiamo studiare il nodo e trovare dei momenti che equilibrino quelli agenti sulle travi:

4-> Taglio sulli pilastri-> M = T*b -> T = M/b

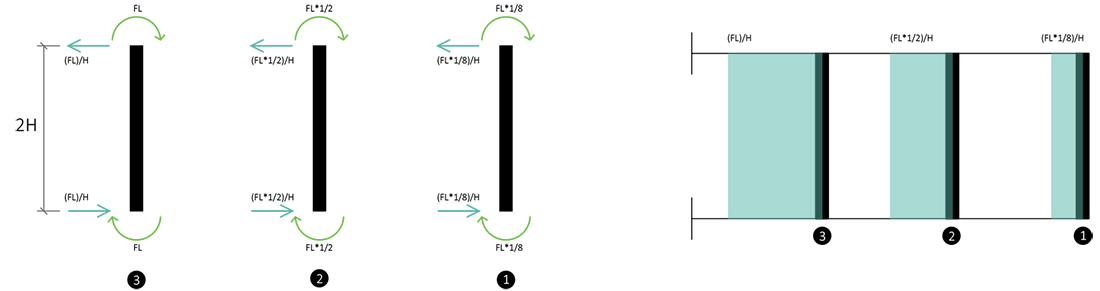
5-> Valori di δ1, δ2, δ3 -> Dopo aver equilibrato tutto possiamo andare a calcolare i valori degli spostamenti:

T₁ = 12EIδ₁/(L³) -> δ_{1 =} FL³/(48EI)

                                 -> δ_{2 =} FL³/(16EI)

                                 -> δ₃₌ FL³/(48EI)