ESERCITAZIONE 1_TRAVE RETICOLARE 3D(SAP)_TRAVE RETICOLARE 2D (SAP+RITTER/NODI)

#1_TRAVE RETICOLARE 3D(SAP)

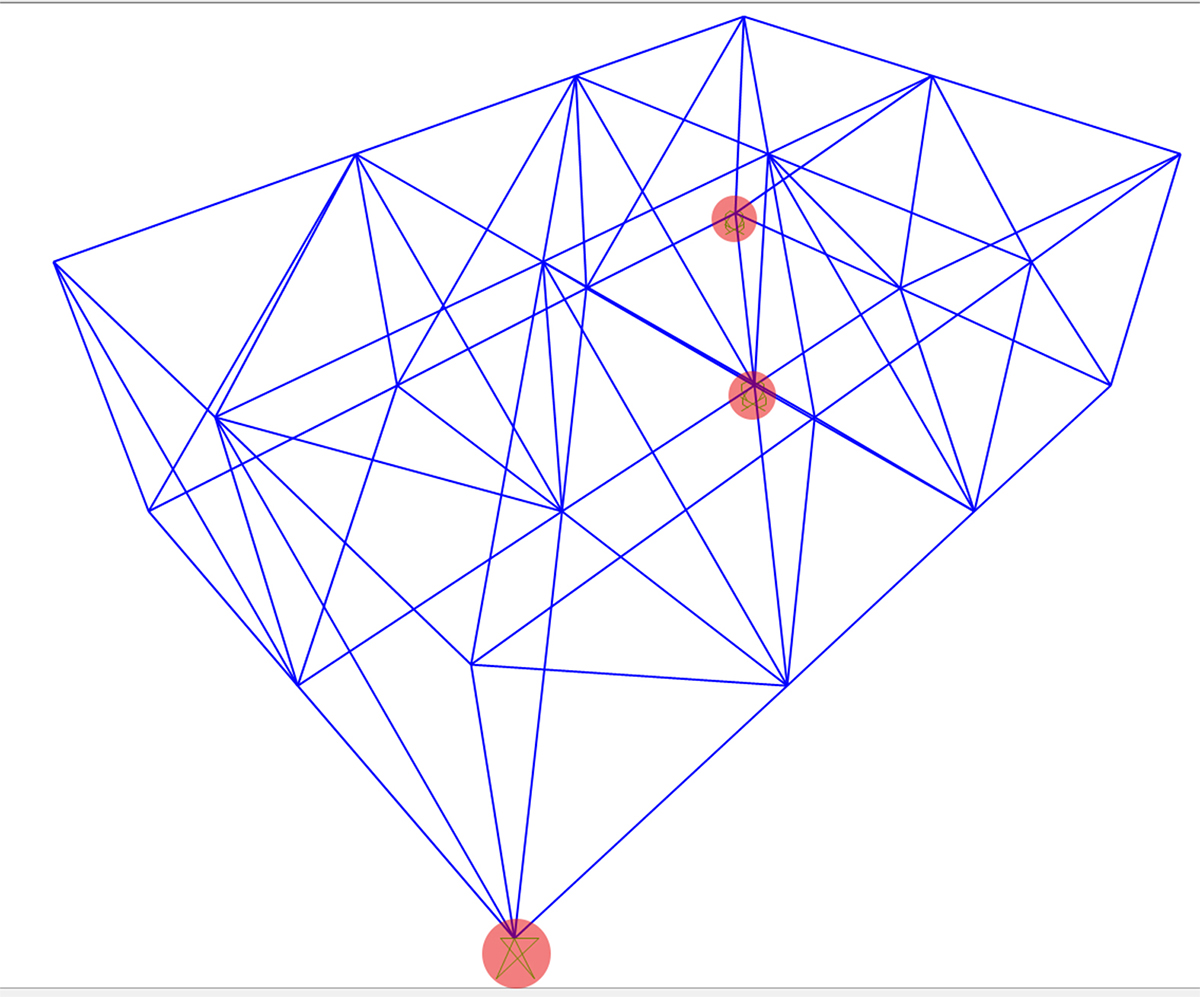
Dopo aver disegnato una struttura reticolare in 3 dimensioni, avente modulo quadrato L x L, con L = 2 m, viene immessa nella in SAP, avendo l'accortezza di separare ogni singola ASTA dalle altre ed aver approssimato  l'errore nei nodi con uno scarto più basso possibile.

Si assegnano i tre vincoli in modo che non siano allineati:

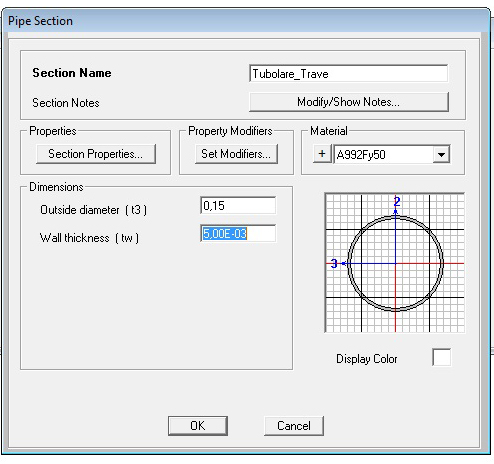
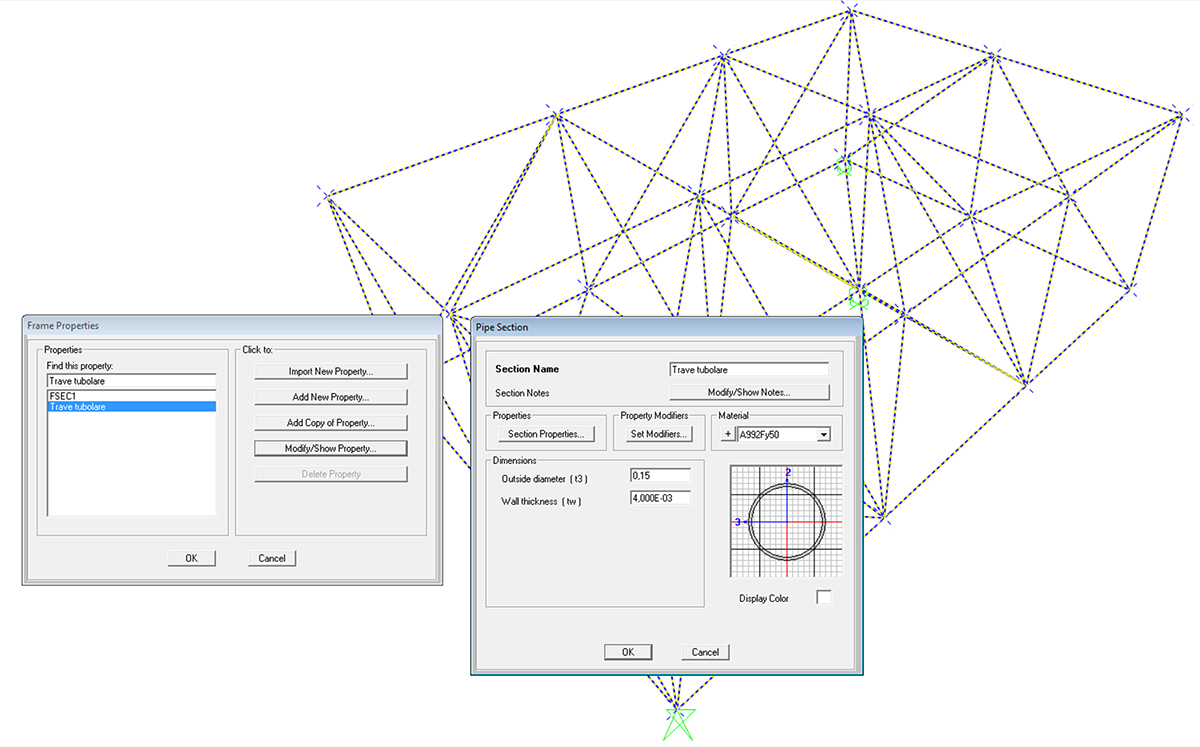
Si definisce una sezione per le ASTE, in questo caso una sezione scatolare cilindrica d'acciaio di spessore 4 mm e diametro 15 mm:

s = 4 mm

d = 15 mm

Si assegnano le Forze puntuali di 40 KN su ogni nodo superiore della struttura e rilascia tutta la struttura dal momento e si elimina il perso proprio della struttura dall'equazione:

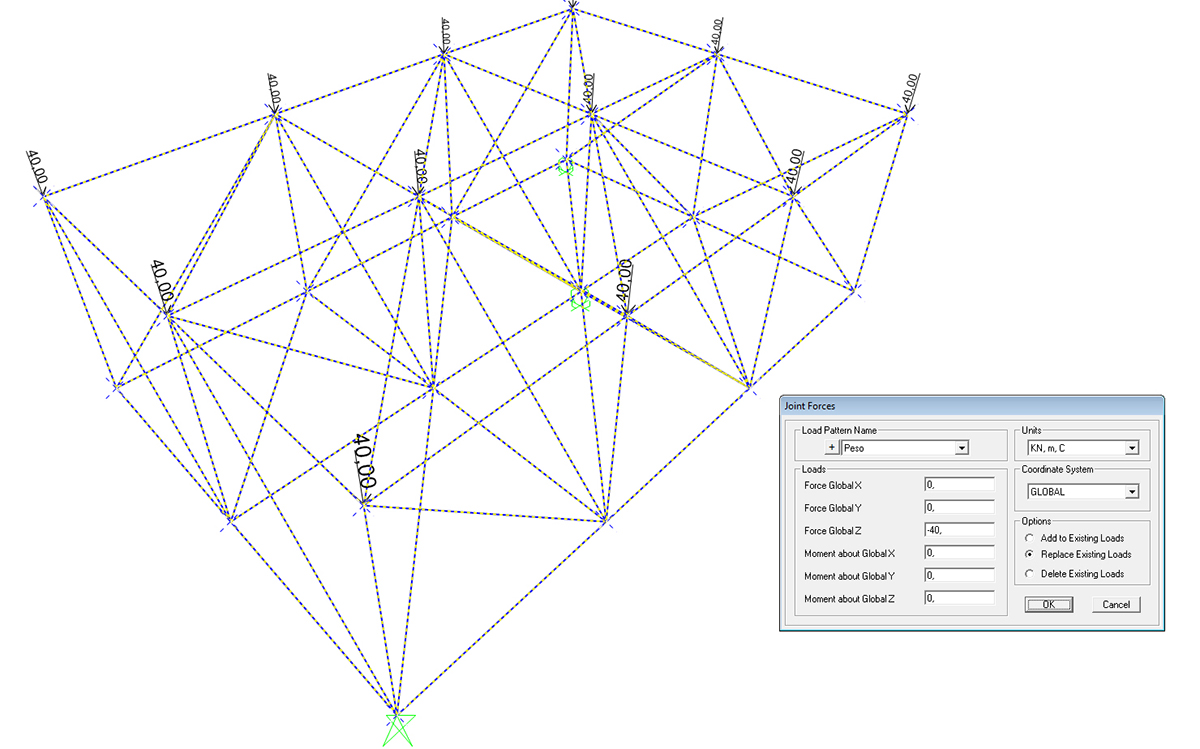
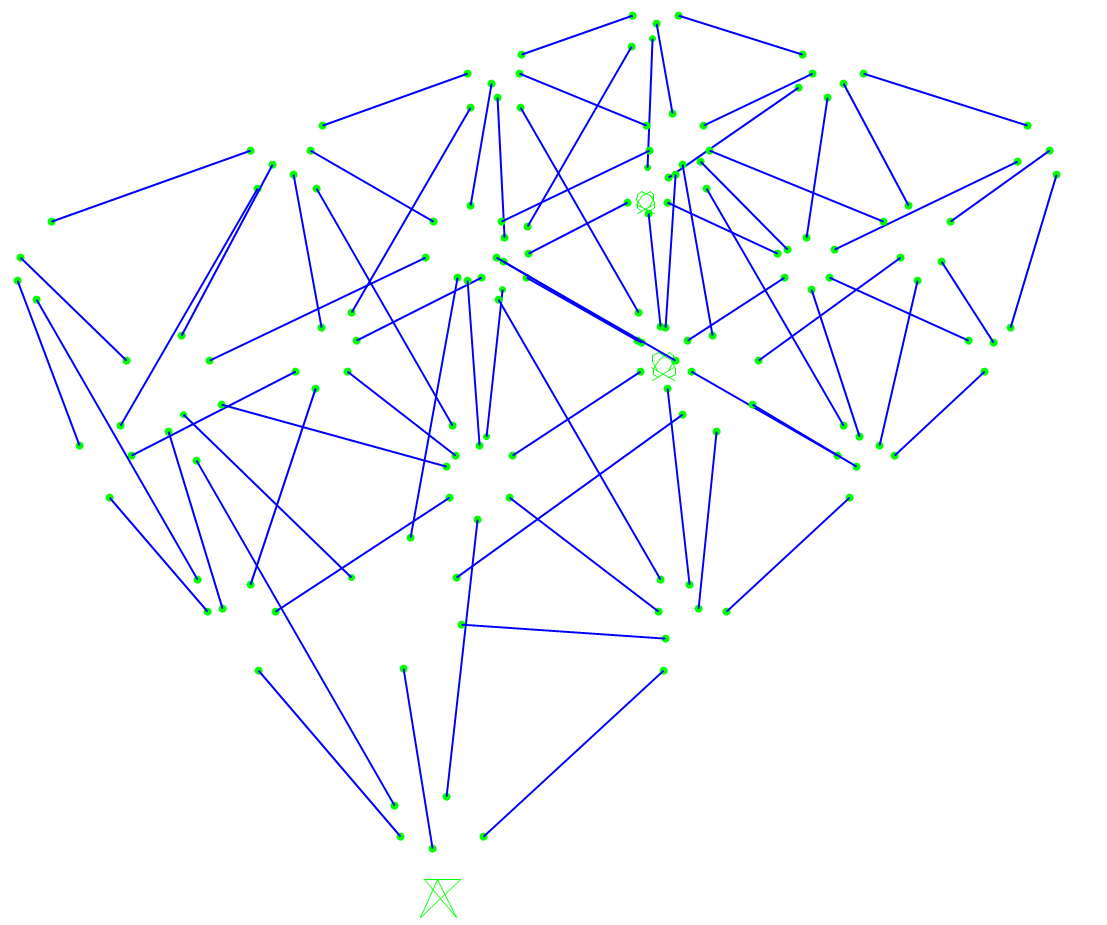
Una volta avviata l' analisi della struttura se ne ricavano i diagrammi della struttura DEFORMATA, e delle sollecitazioni di COMPRESSIONE e TRAZIONE in ogni asta

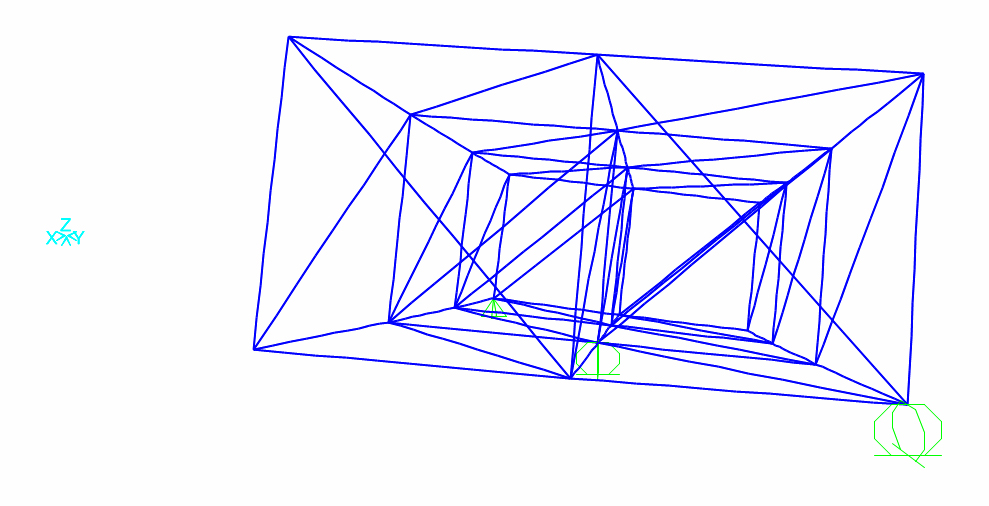
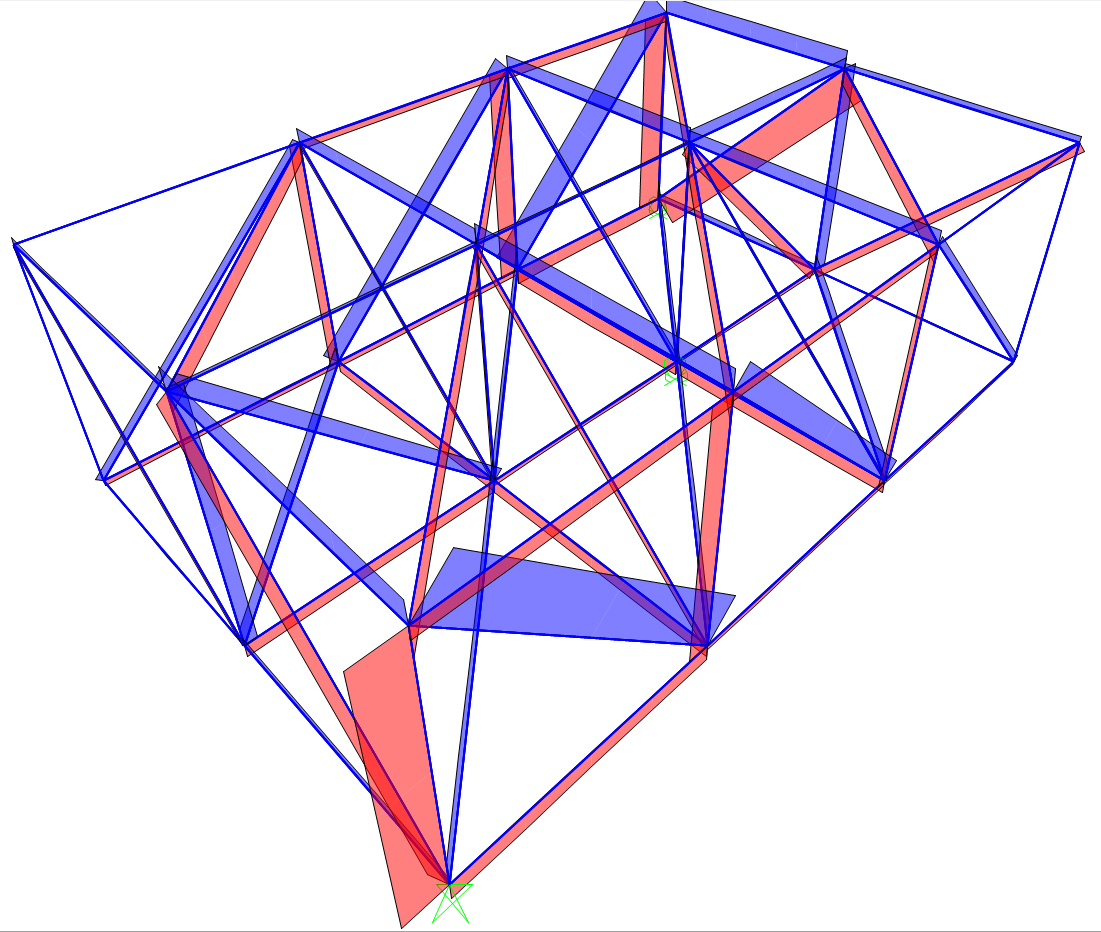
e i valori della TENSIONE interna alle aste:

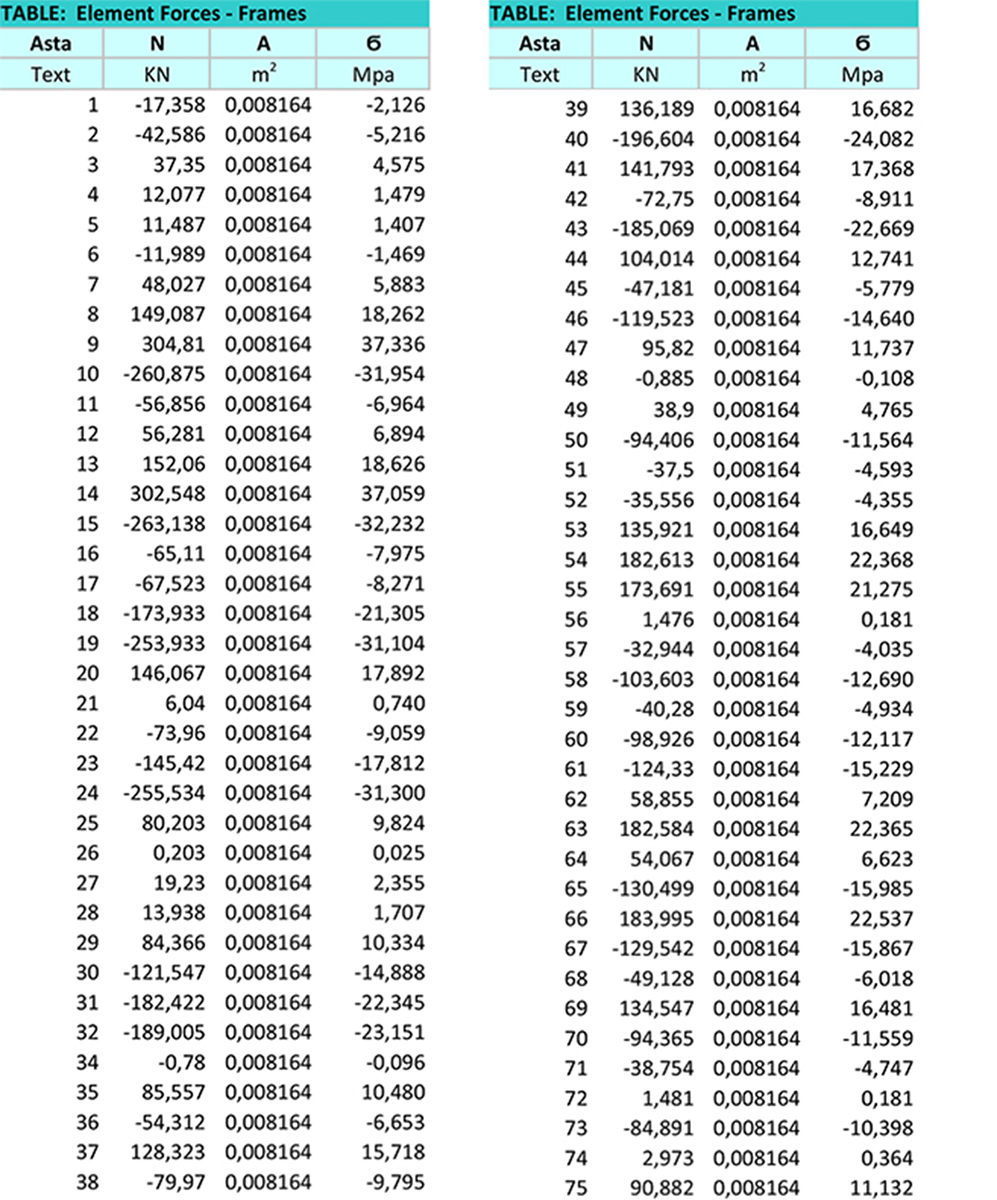
#2_TRAVE RETICOLARE 2D (SAP+RITTER/NODI)

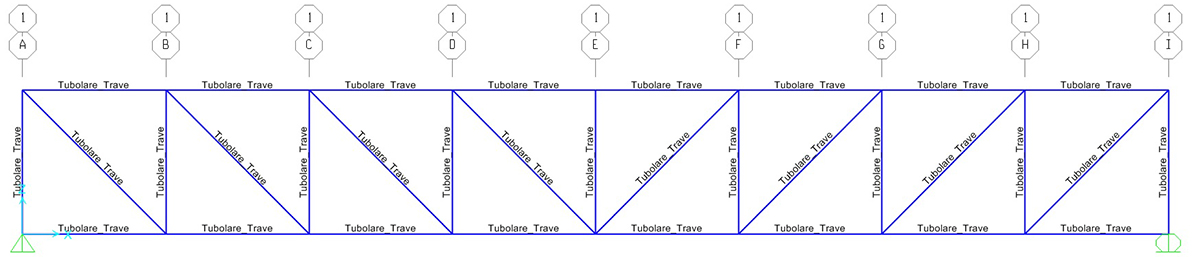
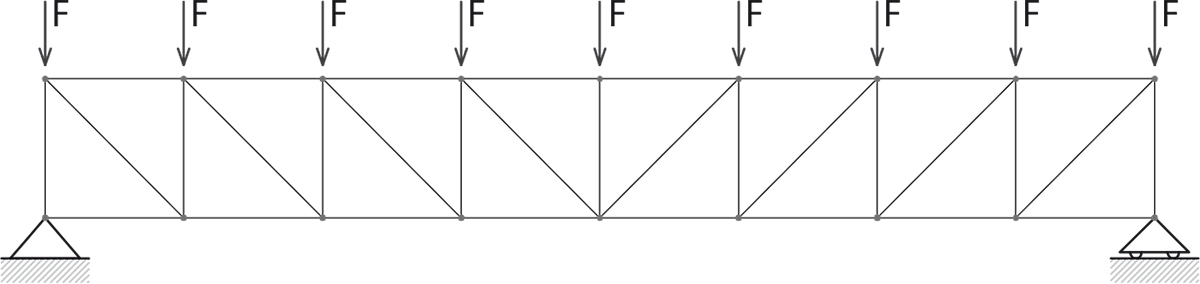
Una travatura reticolare si riconosce semplicemente se le aste hanno solo sforzo normale N di trazione (+) o compressione (-), ed è isostatica in quando è formata da triangoli.

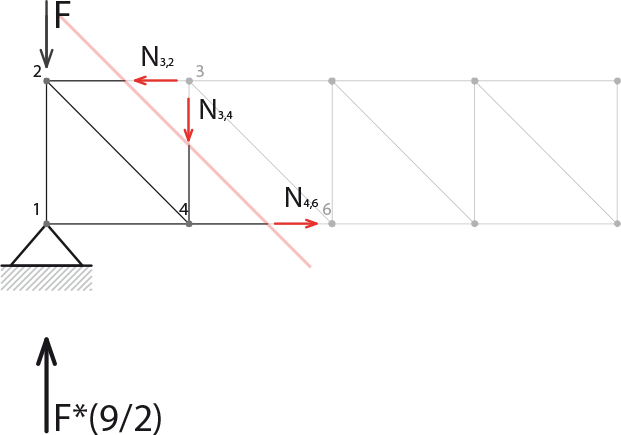
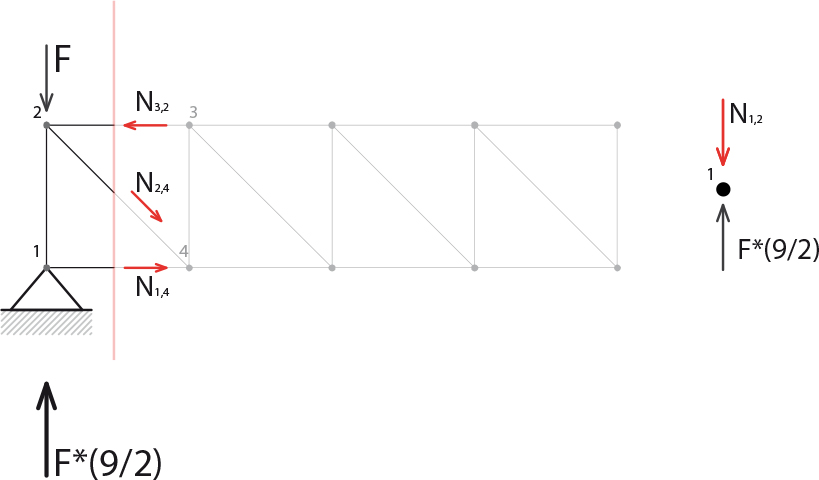
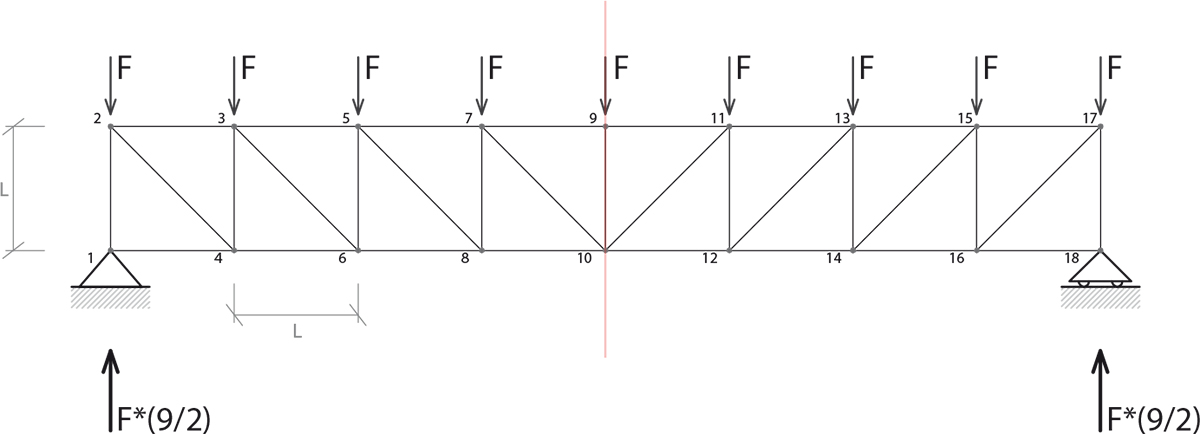
La struttura reticola isostatica è simmetrica, quindi possiamo studiarne una metà, ne numeriamo i nodi e procediamo con lo studio degli sforzi normali all'interno di ogni asta:

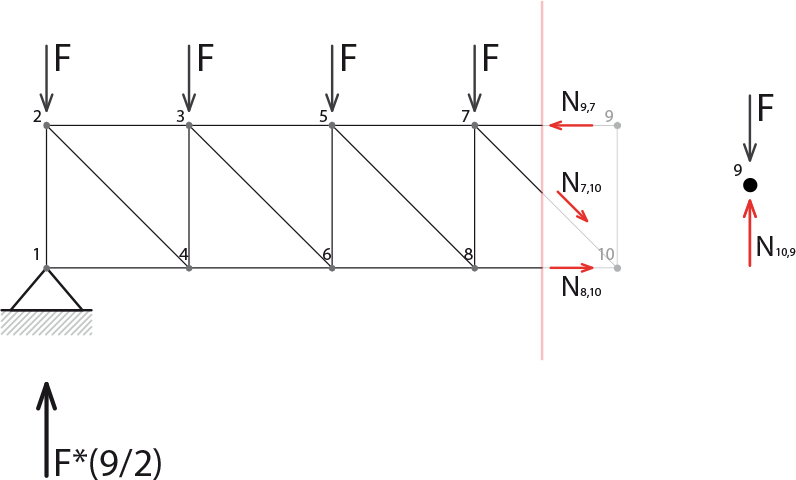
N_9,7*L+F*L+F*2L+F*3L+F*4L-F*(9/2)*4L=0 -> N_9,7=8F

N_8,10*L+F*L+F*2L+F*3L-F*(9/2)*3L=0 -> N_10,8=F*(15/2)

N_7,10(√2/2)-N_9,7+N_{8,10=0 ->} N_7,10=F*(1/√2)

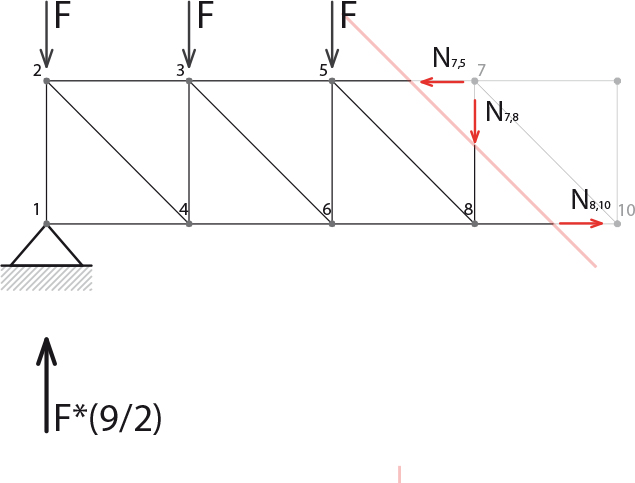
N_10,8=F*(15/2)

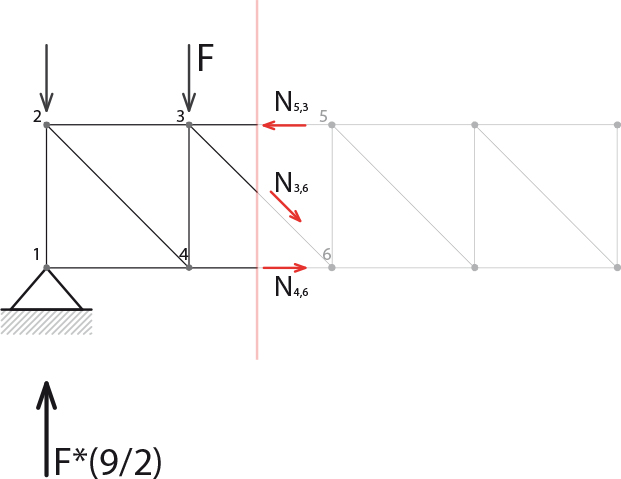
N_7,5*L+F*L+F*2L+F*3L-F*(9/2)*3L=0 ->N_7,5=F*(15/2)

-N_7,8-F-F-F+F*(9/2)=0 -> N_7,8=F*(3/2)

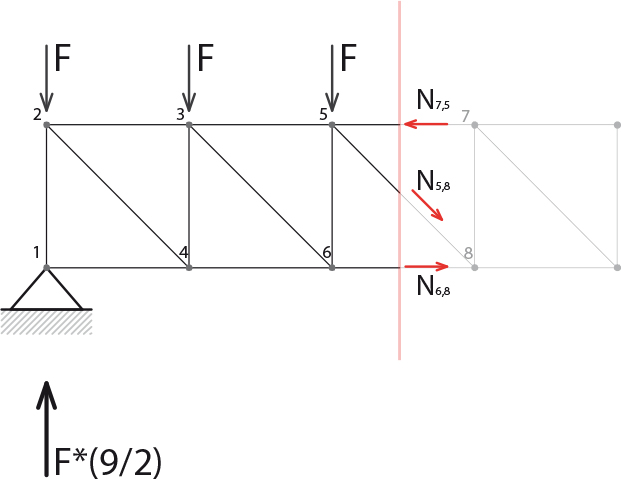
N_7,5=F*(15/2)

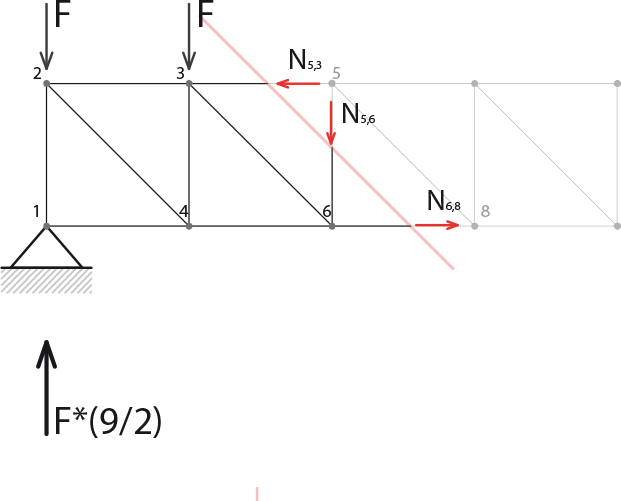
N6,8*L+F*L+F*2L-F*(9/2)*2L=0 ->N_6,8=6F

N_5,8(√2/2)-N_7,5+N_6,8=0->N_5,8=F*(3/√2)

N_5,3=6F

 

N_4,6*L+F*L-F*(9/2)*L=0 ->N_4,6=F*(7/2)

 

N_3,6(√2/2)-6F+F*(7/2)=0 ->N_3,6=F*(5/√2)

 

N_6,4=F*(7/2)

 

N_3,2*L+F*L-F*(9/2)*L=0 ->N_3,2=F*(7/2)

 

-N_3,4-F+F*(9/2)=0 ->N_3,4=F*(7/2)

N3,2=F*(7/2)

 

N1,4=0 

 

N2,4(√2/2)-F*(7/2)=0 ->N2,4=F*(7/√2)

 

N_3,2=F*(7/2)

 

N_1,4=0 

 

N_2,4(√2/2)-F*(7/2)=0 ->N_2,4=F*(7/√2)

 

N_1,2=F*(9/2)

 

Gli sforzi sulla trave sono:

                               

indicando in Blu i puntoni (compressi) e in Rosso i tiranti (tesi).

 

VERIFICA SU SAP

Imposto la trave reticolare in SAP con

L=2 m

F=10 KN

e una sezione cilindrica cava per le aste

                     

Sforzi assiali:

                    

Deformata:              

                     

 

N6,4=F*(7/2)

 

N4,6*L+F*L-F*(9/2)*L=0 ->N4,6=F*(7/2)

 

-N3,4-F+F*(9/2)=0 ->N3,4=F*(7/2)