ESERCITAZIONE 4_TRAVE IPERSTATICA_METODO DELLE FORZE

Il metodo delle Forze consente di risolvere strutture iperstatiche come travi o travi continue su più appoggi, riconducendole a strutture isostatiche di riferimento delle quali sono noti spostamenti e rotazioni, e ponendo come incognite le reazioni vincolari iperstatiche in modo da ristabilire la compatibilità cinematica dei vincoli soppressi.

Risoluzione di una Trave su appoggi, 3 volte iperstatica, con il metodo delle forze.

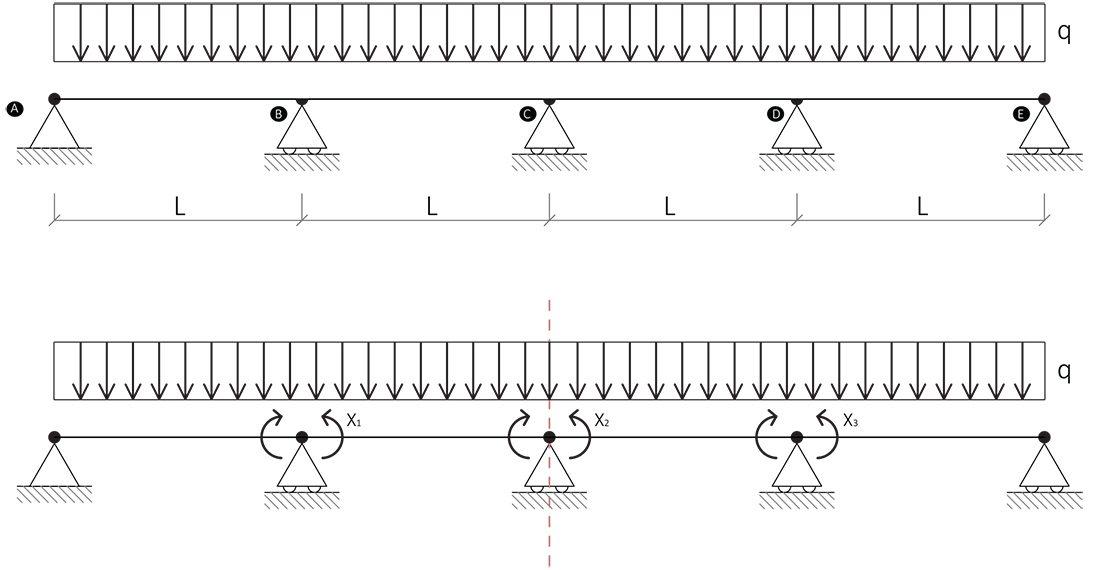
Svincolo le cerniere in B, C, D, rendendole cerniere passanti, e applico tre momenti incogniti X1, X2, X3.

Dobbiamo applicare il principio della sovrapposizione per calcolare gli effetti dovuti al carico q e dai momenti applicati X:

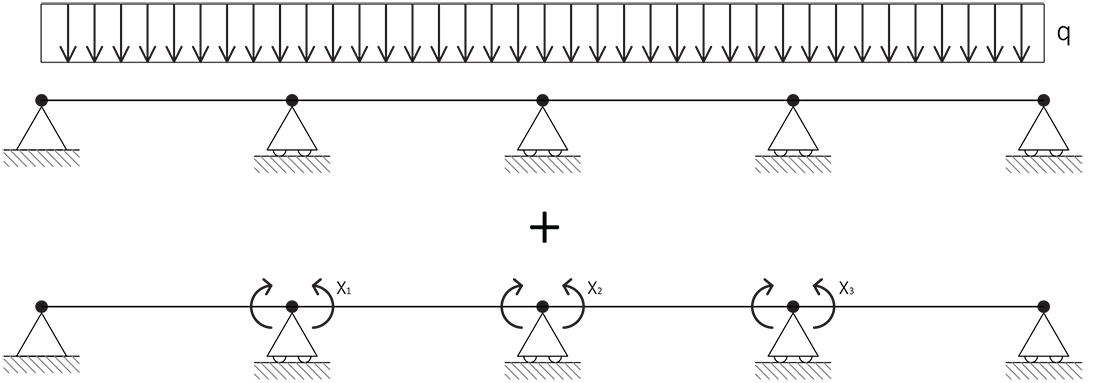
Dovendo ritornare ad una condizione di iperstaticità,

e riordando i valori delle rotazioni dovute al carico ripartito q (pl³/24EI)e le rotazioni Primarie (XL/3EI) e Secondarie (XL/6EI) dovute ai momenti incogniti applicati,

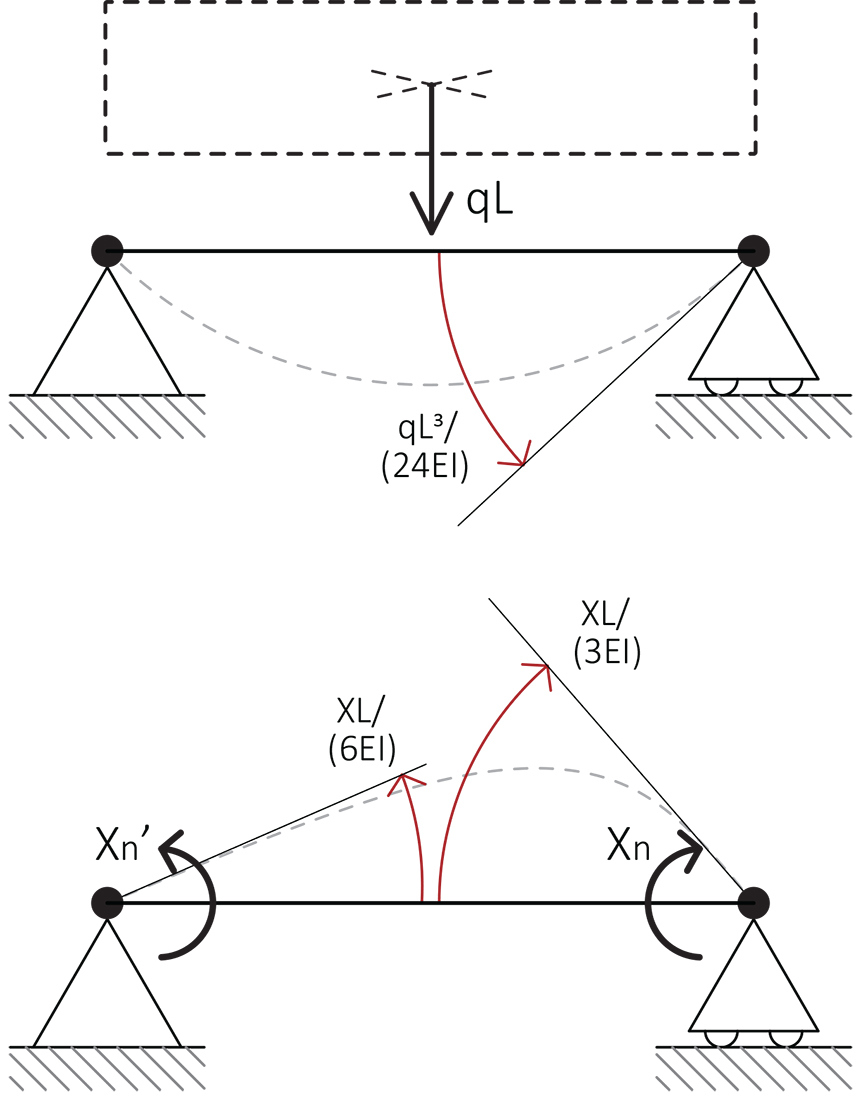
poniamo le rotazioni in ogni carrello uguale a zero, scriviamo queindi le EQUAZIONI DI CONGRUENZA per ogni punto (B, C, D)

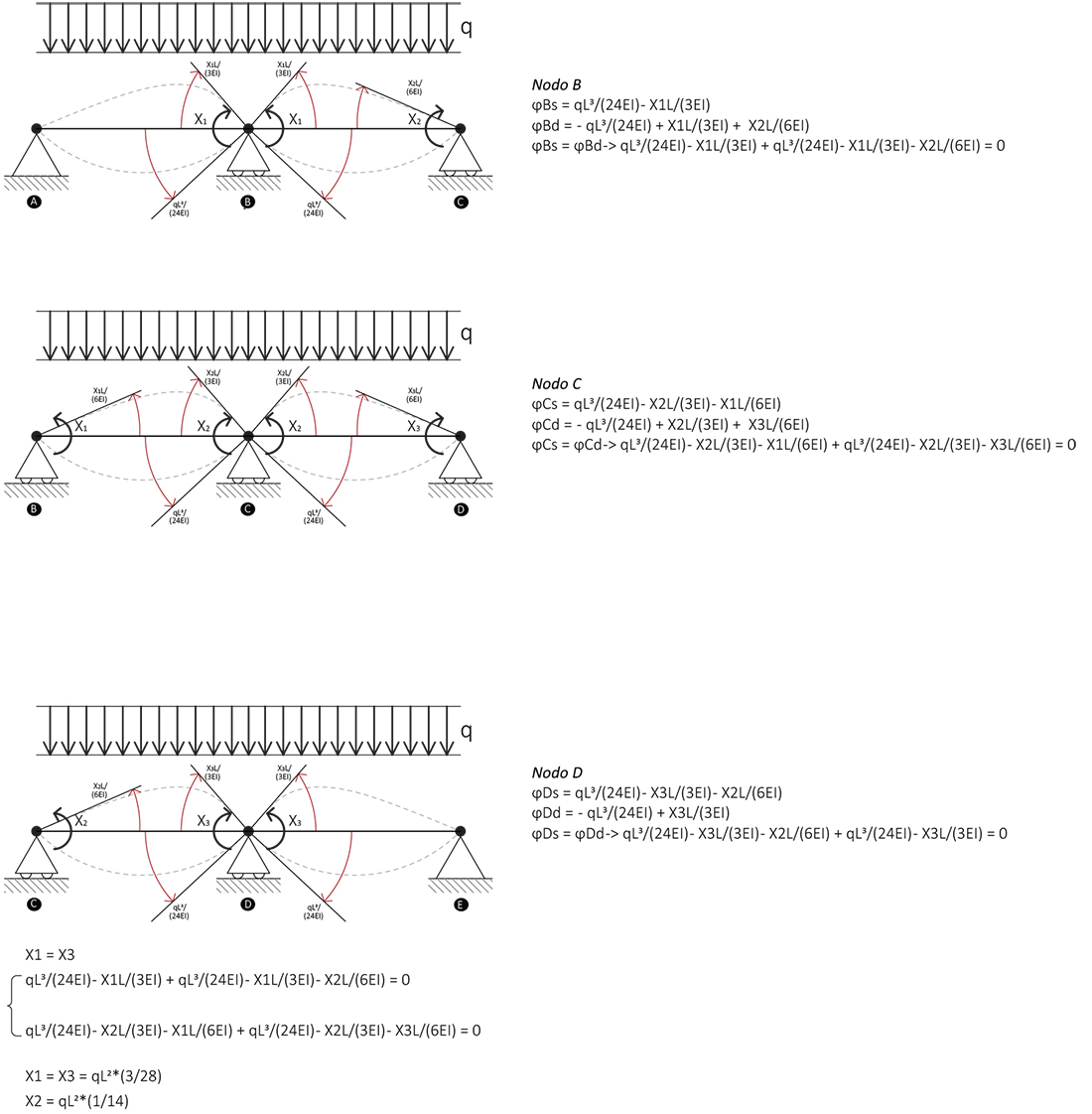
mettendo a sistema i valori delle rotazioni in B e C (con B = D), ricavo i valori dei momenti applicati.

Ora studiamo le reazioni sulla trave, suddivisa in 4 tratti, dovuti al carico ripartito q:

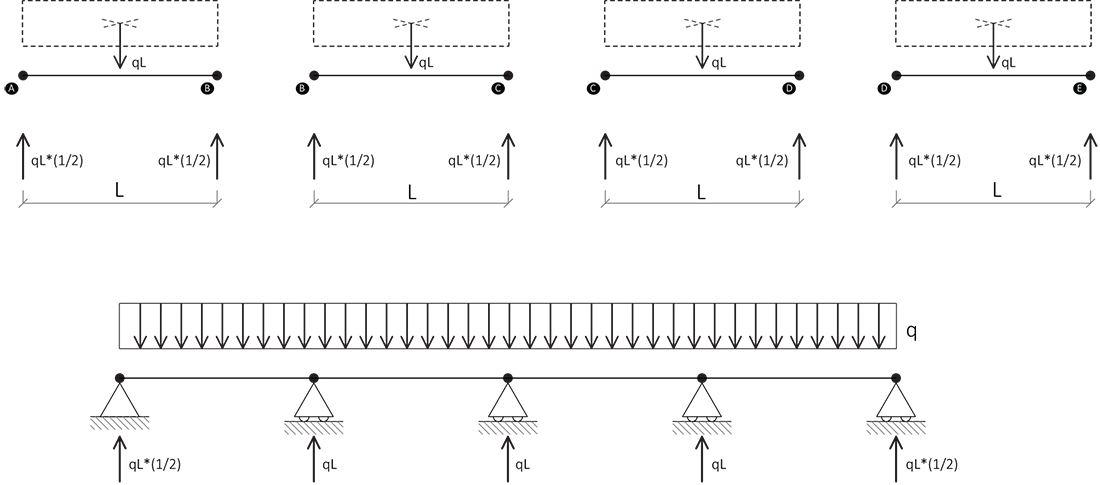
e ai momenti assegnati: X1 e X3

e X2

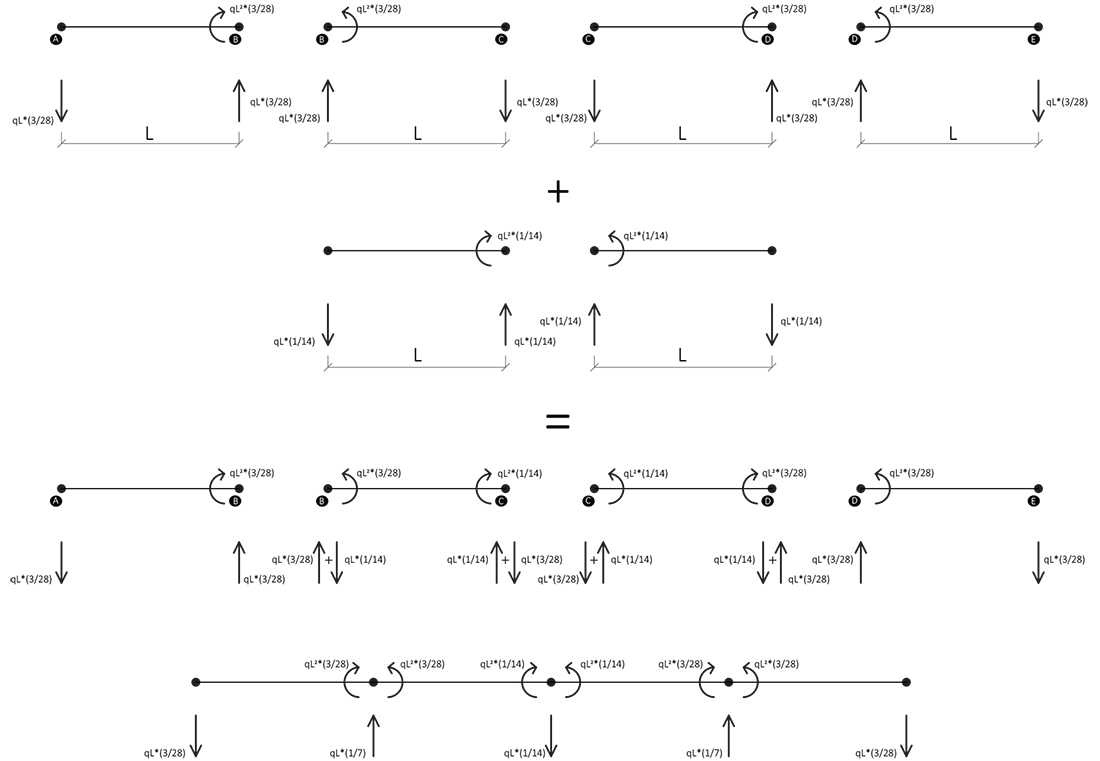
e ottengo le reazioni, i valori degli sforzi di Taglio e Momento Flettente che il carico e i momenti producono sulla trave iperstatica:

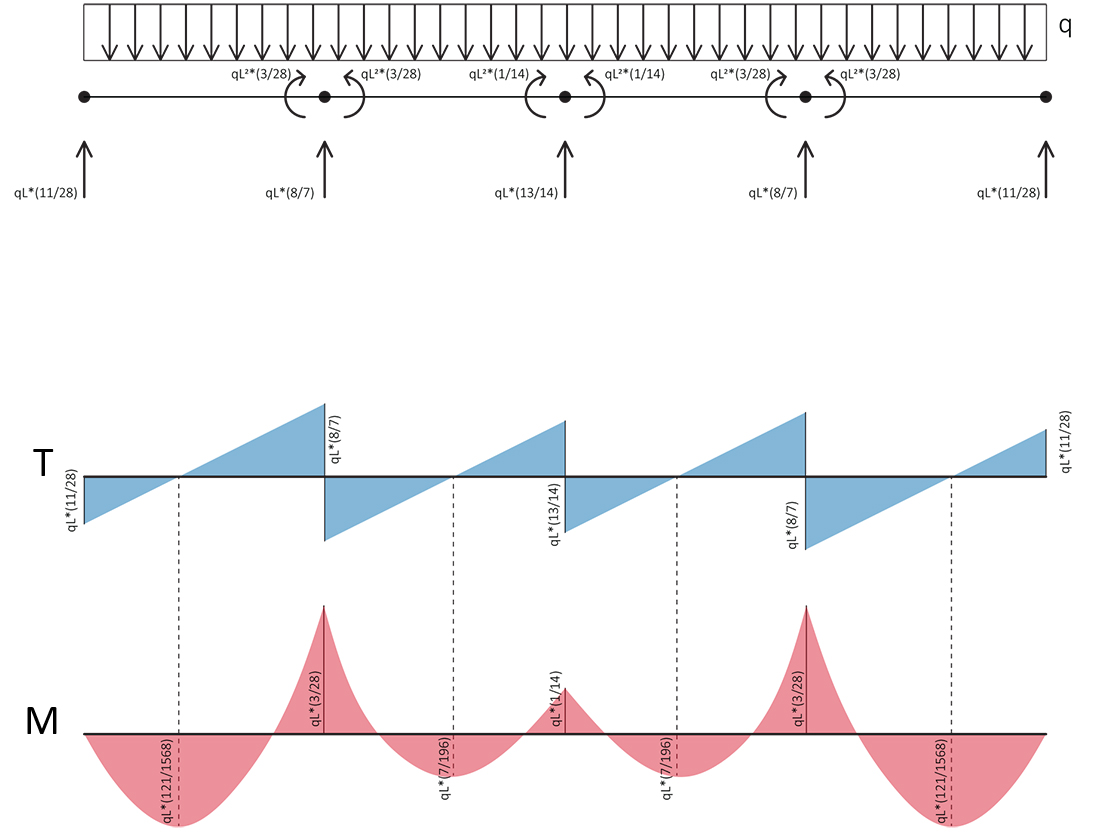
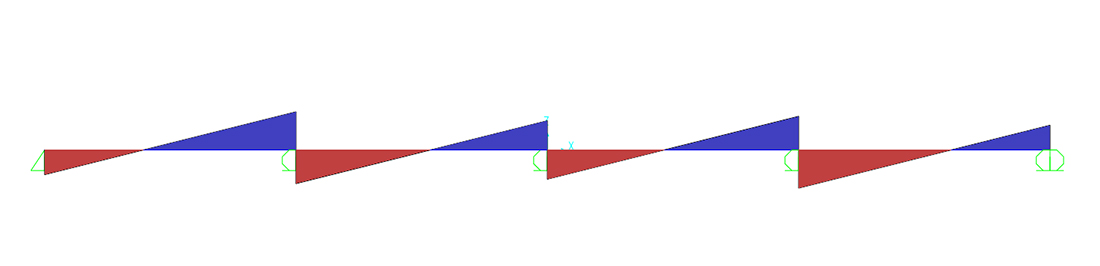
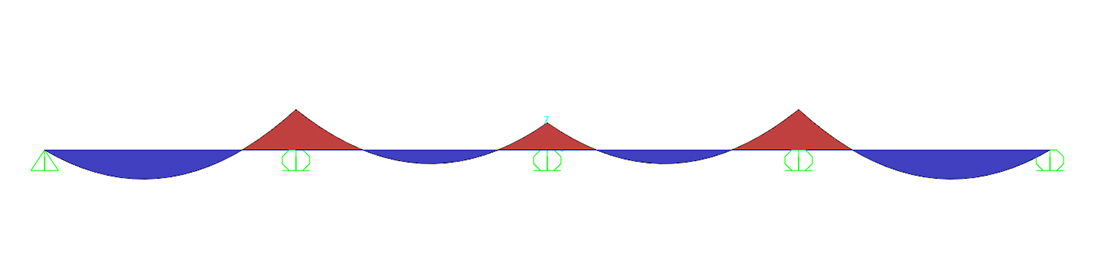
Verifica su Sap degli sforzi calcolati:

Taglio

Momento