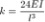Esercitazione5-Telaio Shear Type

Il telaio Shear Type indica la configurazione di una struttura di tipo “portale”. La caratteristica insita a questo telaio è l’indeformabilità della struttura orizzontale la quale fa si che il portale si possa deformare nei soli pilastri, che comunque hanno un movimento limitato dagli incastri alla base e al colmo degli stessi.

Prima di tutto però è bene definire il concetto di rigidezza (k) in quanto è il valore più influente per definire lo spostamento (δ).  La rigidezza è una costante derivata dal materiale che indica la quantità di forza necessaria ad imprimere una deformazione di spostamento unitario, difatti: F=k*δ . Quindi, maggiore è la rigidezza e maggiore dovrà essere la forza impressa per deformare il corpo.

Abbiamo detto dunque che la trave è indeformabile e che vi è mancanza di rotazione  agli estremi quindi và da se che la trave si muove con atto di moto rigido e le deformazioni sono insite nei soli pilastri. Essendo alla base ancorati al terreno, nel caso ci sia (come nel nostro caso) una forza orizzontale spingente (di cui tra l’altro si conosce il valore), l’unico spostamento sarà nel colmo del pilastro e sarà, per tutto quello che abbiamo detto prima, uguale a quello dell’altro pilastro. Lo spostamento derivato definirà il valore δ e darà vita a deformazione di curvatura χ e conseguente momento M, a prescindere dalla quantità del carico.

Tramite l’integrazione della linea elastica:

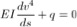
Essendo in questo caso in assenza dicarico: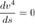

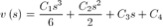
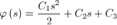
Analizziamo le condizioni al bordo:

ESTREMO BASE

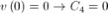
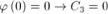
ESTREMO COLMO

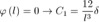
Possiamo quindi riportare le equazioni di spostamento e rotazione:

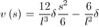
Derivando la rotazione si avrà la curvatura e quindi il momento flettente M e il taglio T.

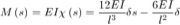
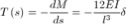
Da queste si possono diagrammare gli sforzi.

Qui sopra si possono vedere i valori delle reazioni vincolari nel pilastro, ma essendo strettamente collegate alla trave sappiamo che i valori vengono trasmessi all’interno della stessa:

Calcoliamo ora lo spostamento d tramite l’equilibrio alla traslazione orizzontale del corpo rigido (trave):