Esercitazione6-Trave Vierendeel a mensola

In questa esercitazione andremo a studiare il comportamento di vari telai Shear Type sovrapposti l’uno all’altro e ribaltati in modo da costituire un sistema di trave che per la sua conformazione avrà delle sollecitazioni inferiori rispetto ad un sistema standard.

Studieremo due casi: il primo quando la nostra trave sarà disposta a mensola mentre il secondo quando la trave sarà incastrata da ambedue le parti.

Trave Vierendeel a mensola:

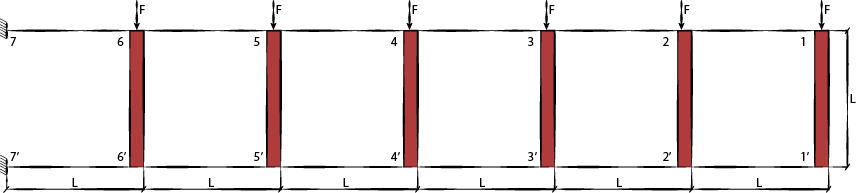
Come abbiamo detto prima la trave Vierendeel è costituita da vari telai Shear Type (nel nostro caso 6) sovrapposti l’uno sull’altro, questo ci consente di usufruire del metodo di risoluzione sfruttato nell’esercitazione del telaio Shear Type.

Il telaio Shear Type ci consente di avere un momento pari a 0 nella mezzeria del pilastro. Questo è un enorme aiuto nel caso si duplichi il telaio più volte dato che i vari segmenti sono disassociati l’uno rispetto all’altro e quindi i valori di momento e taglio diminuiscono ogni qual volta si studia il telaio successivo. Tutto questo ovviamente comporta che i vari segmenti siano della stessa sezione e materiale in modo che il coefficiente di rigidezza sia uguale per ogni segmento. Ciò comporta che ogni segmento abbia un taglio pari alla metà della forza agente. Ovviamente se nel telaio Shear Type si parlava di pilastri deformabili e travi non deformabili, nel sistema di trave Vierendeel sarà l’opposto.

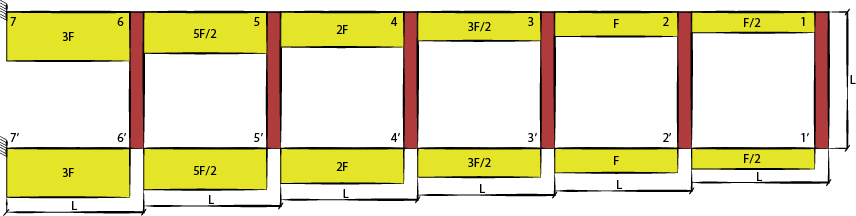
Una volta saputo il taglio si può quindi procedere al calcolo del momento flettente massimo in corrispondenza degli incastri. Per far ciò è sufficiente moltiplicare il valore del taglio del segmento corrispondente per la metà del braccio, ossia L/2:

M₁= F/2 * L/2 = FL/4

M₂= F * L/2 = FL/2

M₁= 3F/2 * L/2 = 3FL/4

M₁= 2F * L/2 = FL

M₁= 5F/2 * L/2 = 5FL/4

M₁= 3F * L/2 = 3FL/2

Trovati i valori di momento sui segmenti di trave andiamo a vedere come gli stessi si trasmettono al pilastro indeformabile e quanto dovrà essere il momento contrastante di ogni pilastro:

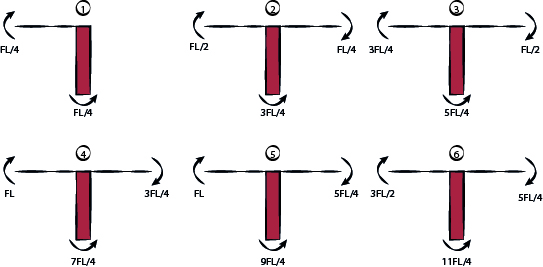
Ne deriviamo cosi il diagramma degli sforzi di momento:

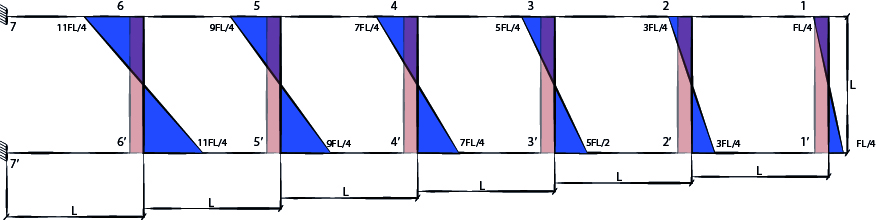
Una volta calcolati i momenti flettenti sul pilastro siamo pronti per calcolare il valore del taglio. Essendo ai due estremi del pilastro i valori del momento uguali possiamo sommare i valori tra di loro e dividerli per la luce in modo da avere il valore del taglio.

T₁ = (FL/4 + FL/4) / L = F/2

T₂ = (3FL/4 + 3FL/4) / L = 3F/2

T₃ = (5FL/4 + 5FL/4) / L = 5F/2

T₄ = (7FL/4 + 7FL/4) / L = 7F/2

T₅ = (9FL/4 + 9FL/4) / L = 9F/2

T₆ = (11FL/4 + 11FL/4) / L = 11F/2

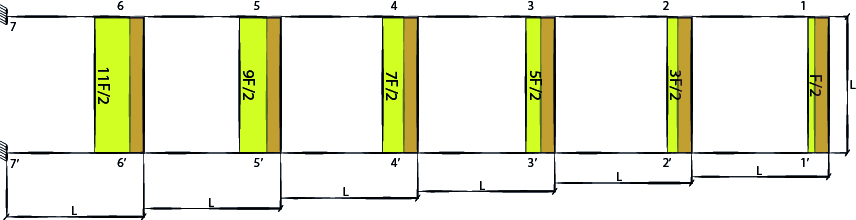
Ora abbiamo il quadro completo. Tutte le forze e sollecitazioni sono state calcolate. Manca a questo punto solamente calcolare lo spostamento δ delle travi. Inizialmente avevamo imposto che tutte le travi avevano una sezione e un materiale uguale, questo implica che tutti i tratti di trave abbiano la medesima rigidezza che, come avevamo calcolato nell’esercizio del telaio Shear Type, ha un valore di 12EI/L³. Conoscendo, come già detto, il valore del taglio per ogni campata otteniamo:

F/2 = T = 12EI/L³ * δ₁ àδ₁ = FL³/24EI

F = T = 12EI/L³ * δ₂ àδ₂ = FL³/12EI

3F/2 = T = 12EI/L³ * δ₃ àδ₃ = FL³/8EI

2F = T = 12EI/L³ * δ₄ àδ₄ = FL³/6EI

5F/2 = T = 12EI/L³ * δ₅ àδ₅ = 5FL³/24EI

3F = T = 12EI/L³ * δ₆ àδ₆ = FL³/4EI

Da cui ne possiamo derivare la configurazione deformata:

            Verifica in SAP2000

Per la verifica in SAP2000 possiamo usare il modello “2D Frames”. Disegnamo la trave del nostro esercizio e impostiamo sezione e materiale. Per i pilastri però c’è bisogno di un coefficiente di rigidezza infinitamente elevato perché è indeformabile. Questo implica che il materiale assegnato ai pilastri sarà diverso rispetto a quello dato ai segmenti di trave. In questo modo sarà possibile determinare i valori giusti anche in SAP:

Deformata:

Taglio:

Momento: