Esercitazione7-Trave Vierendeel doppiamente incastrata

Trave Vierendeel doppiamente incastrata:

Come accennato all’inizio dell’esercitazione la seconda parte è dedita allo studio della stessa struttura analizzata in precedenza, con l’unica differenza che non sarà più a mensola ma sarà doppiamente incastrata agli estremi. In questo caso possiamo sfruttare la simmetria della struttura.

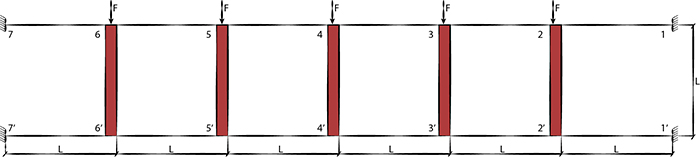
Lavoriamo come nell’esercizio precedente e quindi andiamo a calcolare il taglio sulle travi. In questo caso però bisognerà stare attenti perché nel punto 4, baricentro della simmetria, avremo una forza suddivisa in F/2 a destra e F/2 a sinistra.

Dal valore del taglio ne deriviamo quello di momento (moltiplico il taglio per metà della luce):

M₄= F/4 * L/2 = FL/8

M₅= 3F/4 * L/2 = 3FL/8

M₆= 5F/4 * L/2 = 5FL/8

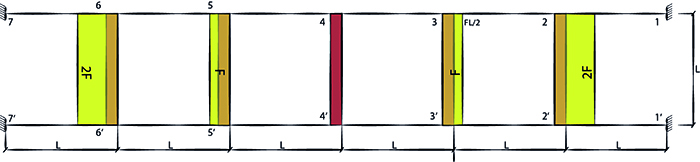
A questo punto possiamo riportare i momenti agenti sui pilastri, ricordandoci di unire il momento nel punto 4 a destra e a sinistra:

Ovviamente i punti 3 e 2 saranno gli opposti dei punti 5 e 6.

Ora, avendo i valori dei momenti, determiniamo il valore del taglio dei pilastri:

T₆ = (FL + FL) / L = 2F

T₅ = (FL/2 + FL/2) / L = F

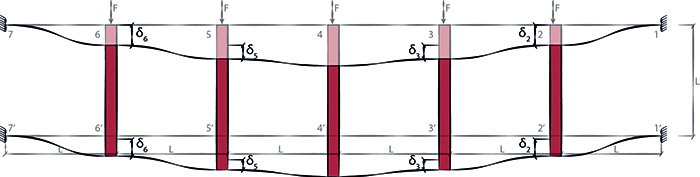
Andiamo quindi a calcolare il valore degli spostamenti:

F/4 = T = 12EI/L³ * δ₄ --> δ₄ = FL³/48EI

F = T = 12EI/L³ * δ₅ --> δ₅ = FL³/16EI

3F/2 = T = 12EI/L³ * δ₆ --> δ₆ = 5FL³/48EI

Possiamo quindi disegnare la nostra deformata:

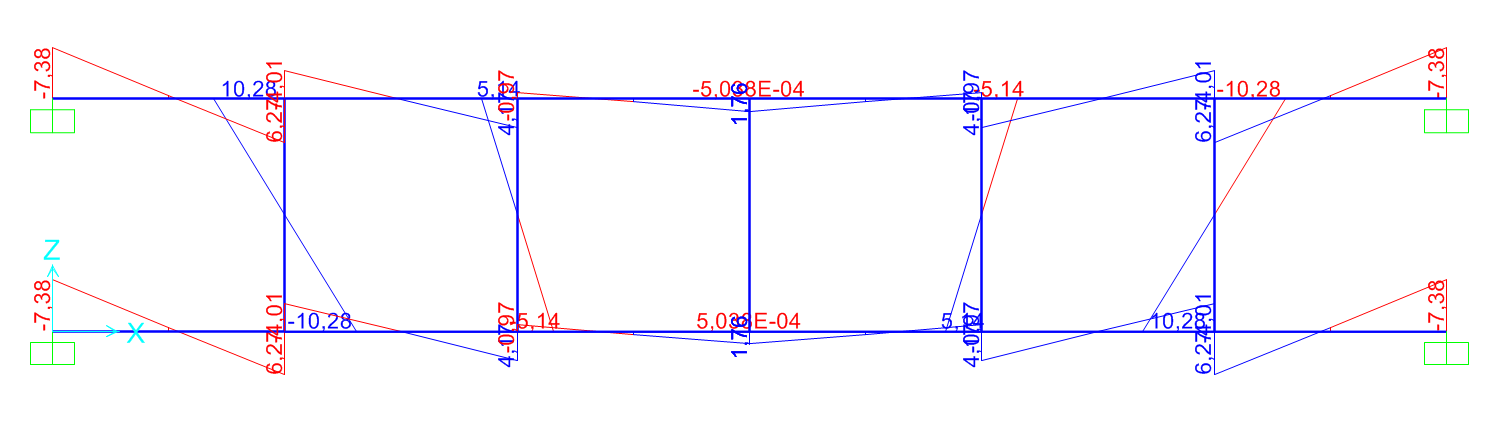
            Verifica in SAP2000

Come abbiamo fatto per l’esercizio precedente risolviamo la struttura in SAP, ricordandoci sempre di dare una rigidezza infinita ai pilastri:

Deformata:

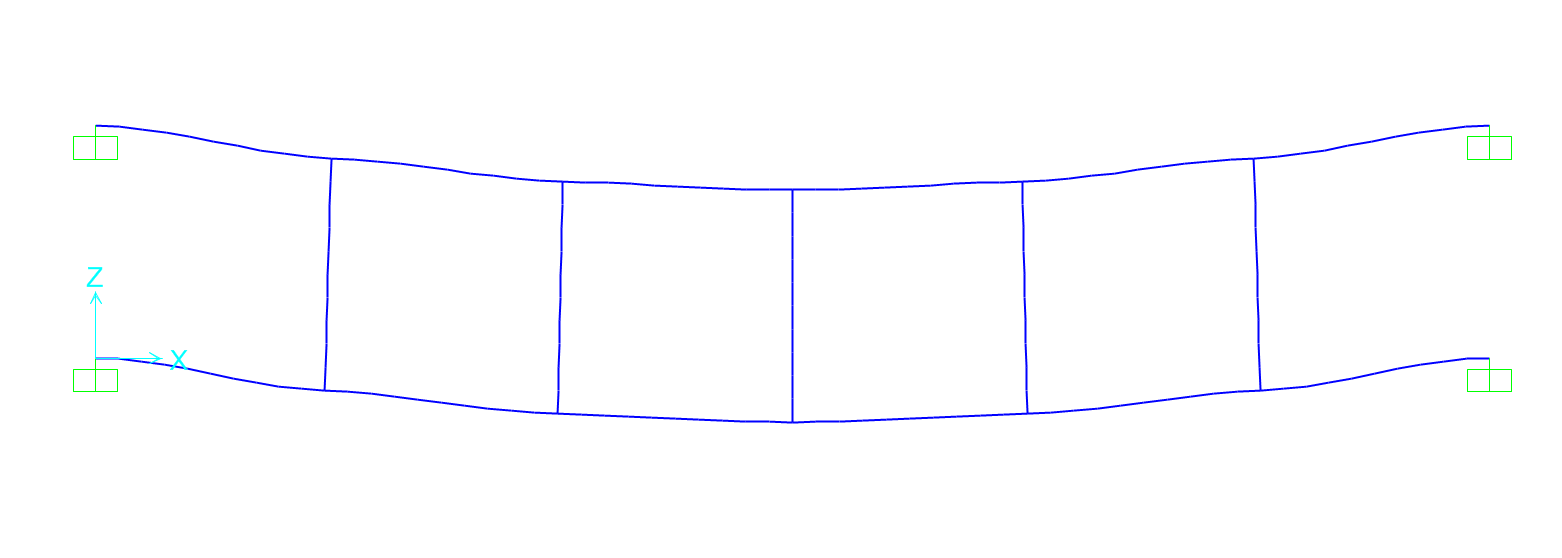
Taglio:

Momento: