Esercitazione: Trave Vierendeel

Trave Vierendeel doppiamente appoggiata

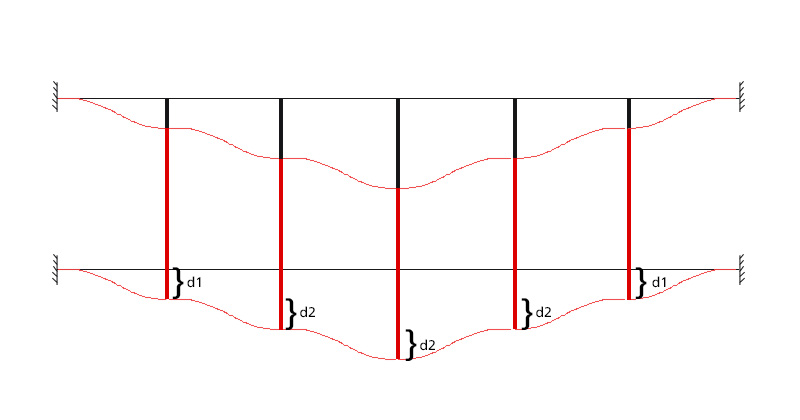
Possiamo immaginare la nostra trave come una sequenza di cinque strutture shear-type unite insieme.
Un telaio shear-type prevede una trave infinitamente rigida che non si deforma con il deformarsi dei pilastri.

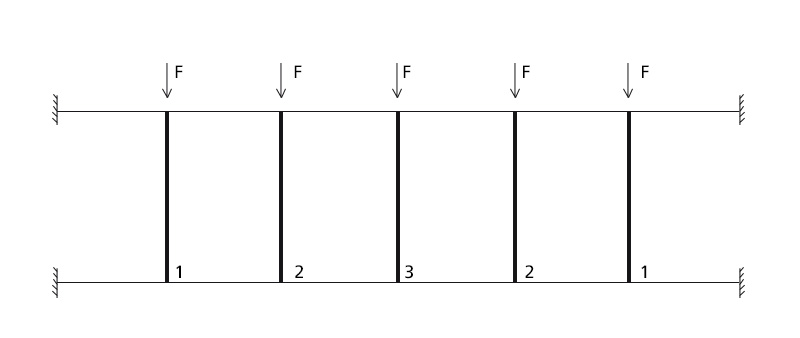
Per quanto riguarda i carichi immaginiamo di avere una sequenza di forze concentrate F sui nodi.

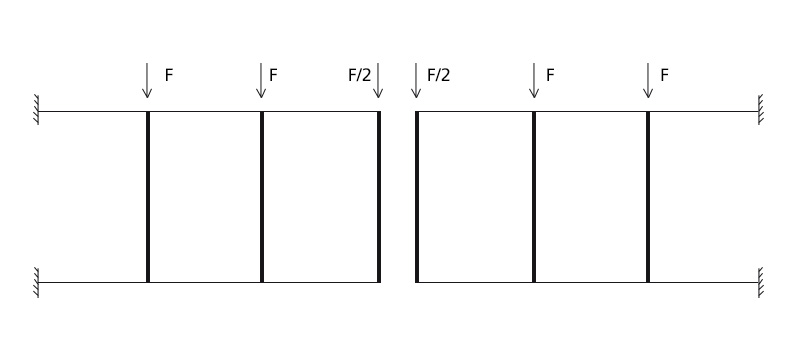
Prima di andare a calcolare tagli e momenti della struttura possiamo scinderla in due parti. Il comportamento sarà simmetrico
nelle due parti del telaio.

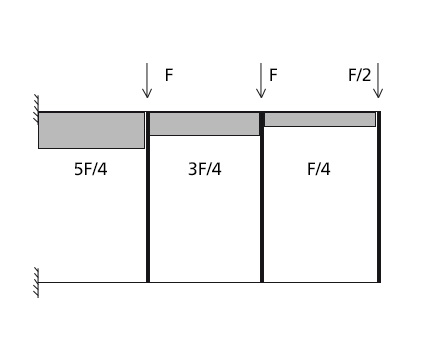
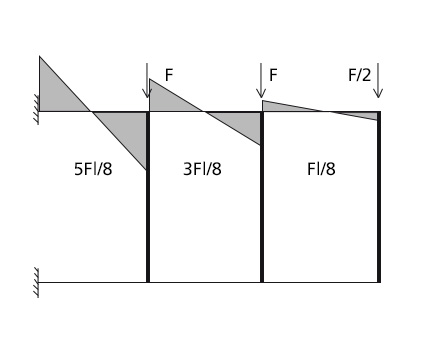
A questo punto vado a calcolare il taglio nelle tre aste (metà struttura):

T(0-1)=5F/4

T(1-2)=3F/4

T(2-3)=F/4

Faccio lo stesso per quanto riguarda il momento:

M(0-1)=5Fl/8

M(1-2)=3Fl/8

M(2-3)=Fl/8

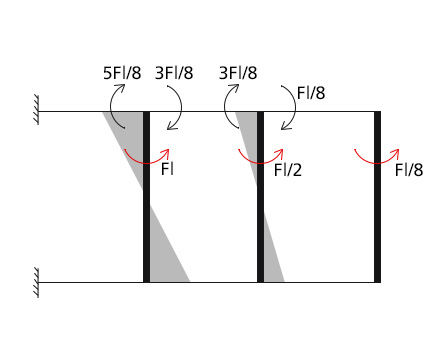
Conoscendo tagli e momenti sarà ora possibile calcolare il momento in ogni singola trave dei vari telai shear-type che compongono la struttura.
Ogni asta è soggetta ai momenti dei due pilastri che la incontrano:

Asta(1) = [5Fl/8] + [3Fl/8] = Fl

Asta(2) = [3Fl/8] + [Fl/8]   = Fl/2

Asta(3) = Fl/8

Ora sapremo che nel calcolo dei tagli dei pilastri dovremo equilibrare i momenti agenti nei pilastri.

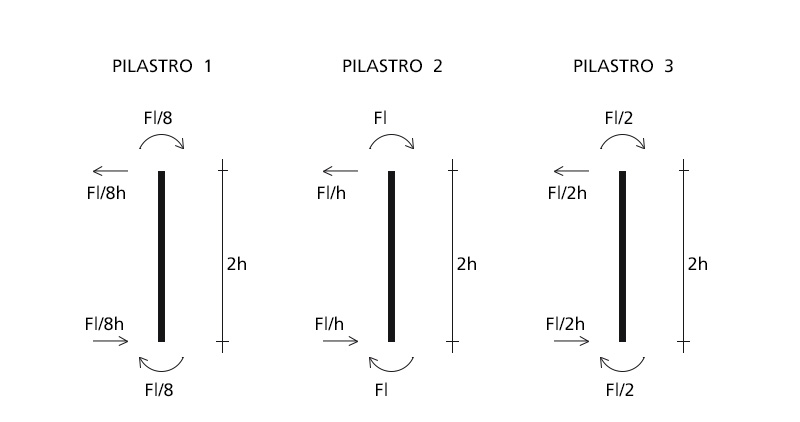
So che la rigidezza è uguale in tutti i pilasti [(12EJ/l^3)*δ]  mentre a variare è il taglio.

T(0-1)= 5F/4 = (12EJ/l^3)*δ           F(0-1)= 48EJδ/5l³                    δ= 5Fl³/48EJ                                     

T(1-2)=3F/4 = (12EJ/l^3)*δ            F(1-2)= 16EJδ/l³                      δ= Fl³/16EJ

T(2-3)=F/4 = (12EJ/l^3)*δ             F(2-3)= 48EJδ/l³                       δ= Fl³/48EJ