Esercitazione8-Ripartizione forze orizzontali

In questa esercitazione dovremo analizzare un impalcato strutturale soggetto a forze orizzontali. Lo studio verterà sul calcolo della rigidezza traslante K_δ, della traslazione δ lungo la direzione della forza agente, sulla rigidezza rotazionale K_φ e quindi sulla rotazione φ intorno al centro delle rigidezze.

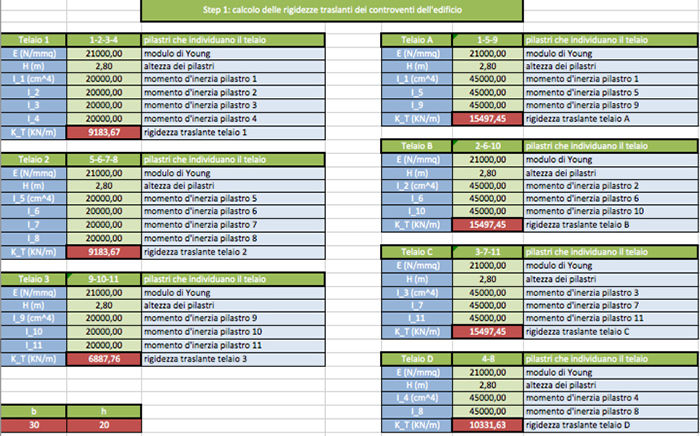
Questo impalcato è formato da 7 telai ognuno dei quali comprende pilastri di grandezza 30x20cm, da cui i momenti d’inerzia:

STEP 1

In questo step si tabellano i telai dando ad ognuno dei dati precisi che sono: modulo di Young (E), altezza H e i valori dei momenti d’inerzia per ogni pilastro in base all’asse di rotazione. Si può quindi procedere al calcolo della rigidezza traslante K_δ di ogni telaio.

K_δ = ΣK_δ                Κ = 12EI/h³

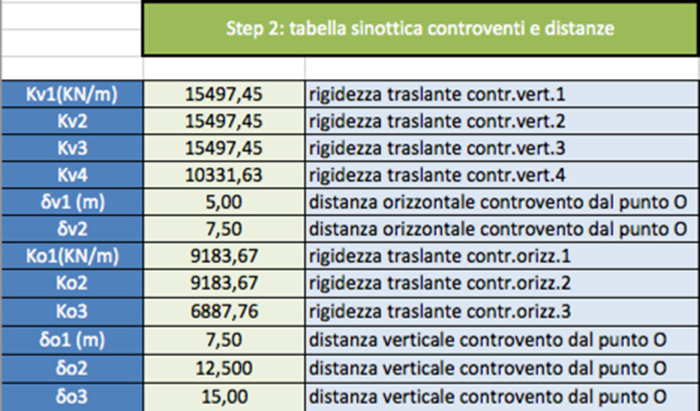
STEP 2

In questo step raccoglieremo tutte le informazioni analitiche delle distanze dei vari telai da un punto di origine O e i valori delle rigidezze traslanti dei telai.

STEP 3

Ora bisognerà trovare il centro delle masse. Il passaggio è abbastanza semplice: si divide la forma della pianta in forme semplici con cui abbiamo facilità nel trovare il baricentro, a questo punto si tratta solo di attuare una media ponderata tra le aree delle suddette forme semplici e moltiplicarle con le distanze dal punto di origine.

G_X = [(X₁*A₁)+ (X₂*A₂)] / A_TOT

G_Y = [(Y₁*A₁)+ (Y₂*A₂)] / A_TOT

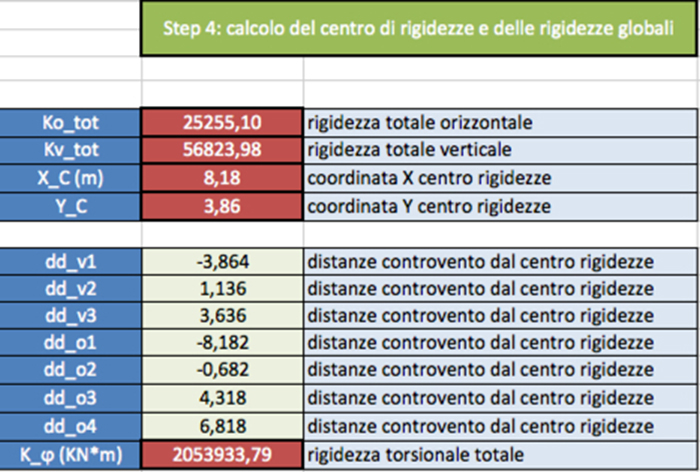
STEP 4

Quindi ora si passa alla determinazione del centro delle rigidezze (C).

X_C = (∑_i K_iv * d_iv) / K_{v_tot}                       Y_C = (∑_i K_io * d_io) / K_{o_tot}

Una volta trovato il centro delle rigidezze si dovranno calcolare le distanze di ogni telaio da C. A questo punto siamo in grado di calcolare la rigidezza torsionale K_φ.

Kφ = ∑i Ki * ddi2

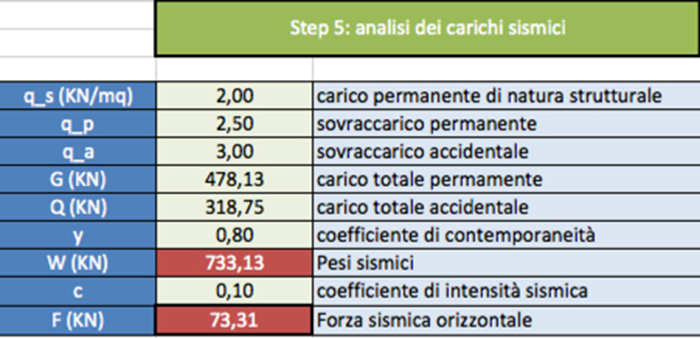
STEP 5

Si esegue ora l’analisi dei carichi sismici allo SLE (perché non viene tenuto in conto γ) tramite il carico permanente totale G (somma dei carichi per l’area dell’impalcato) ed il carico totale accidentale Q (carico accidentale per l’area). Ne consegue che vi possiamo determinare i pesi sismici W: W = G + (Q * y).          y=coefficiente di contemporaneità.

Si procede dunque a trovare la forza sismica orizzontale F: F = W / c.    c=coefficiente di intensità sismica.

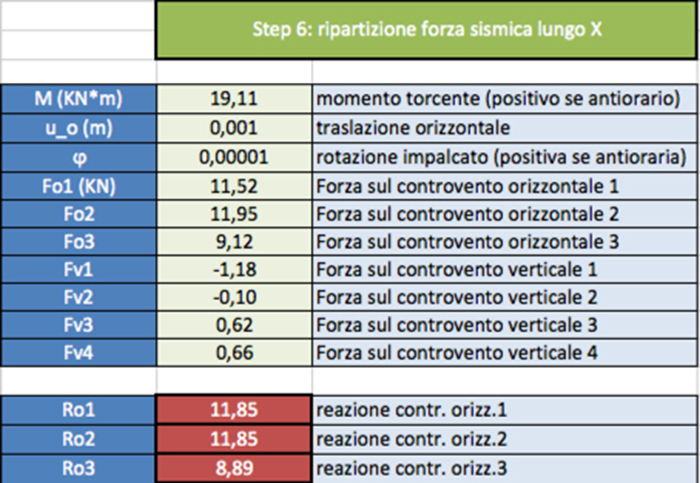
STEP 6-7

Siamo quindi in grado di quantificare la forza sismica orizzontale F lungo i due assi x/y per ogni controvento. Non essendo nello stesso punto il centro delle masse e il centro delle rigidezze il sistema ruoterà dando vita ad una traslazione δ ed una rotazione σ. Questa rotazione genera un momento torcente M che dovremo andare a calcolare.

Asse X:

M = F *(Y_c – Y_G)

F_oi = K_oi (u_x + dd_oi * φ)

F_vi = K_vi (dd_vi * φ)

Asse Y:

M = F *(X_c – Y_G)

F_oi = K_oi (dd_oi * φ)

F_vi = K_vi (u_y + dd_vi * φ)