Esercitazione 6 - Ripartizione delle forze orizzontali in una struttura in cemento armato

RIPARTIZIONE DELLE FORZE ORIZZONTALI IN UNA STRUTTURA IN CEMENTO ARMATO

In questo esercizio si analizza una struttura a telaio in cemento armato, con lo scopo di ricavare la rigidezza nei confronti delle forze orizzontali di ciascun telaio di cui essa è composta, la posizione del centro di massa della struttura, quella del centro delle rigidezze e in base alla distanza tra questi ultimi gli spostamenti che la struttura compie sotto l’azione di un sisma, considerando come si ripartiscono le forze orizzontali sui diversi telai.

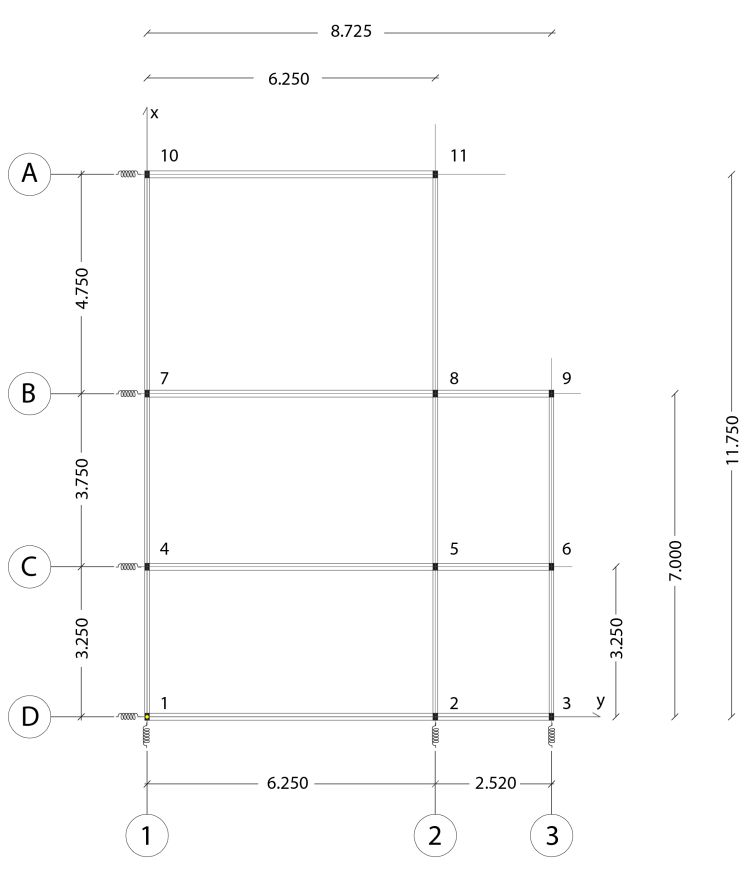
Il primo passo consiste nel calcolare la rigidezza di ogni telaio in cemento armato. Questo valore è strettamente legato alla rigidezza dei singoli pilastri che lo compongono, definita dalla geometria e il materiale di cui sono composti.

In questa tabella sono riassunti i valori delle rigidezze di nostro interesse e le distanze a cui i telai si trovano rispetto all’origine, fissata nel vertice inferiore sinistro della pianta.

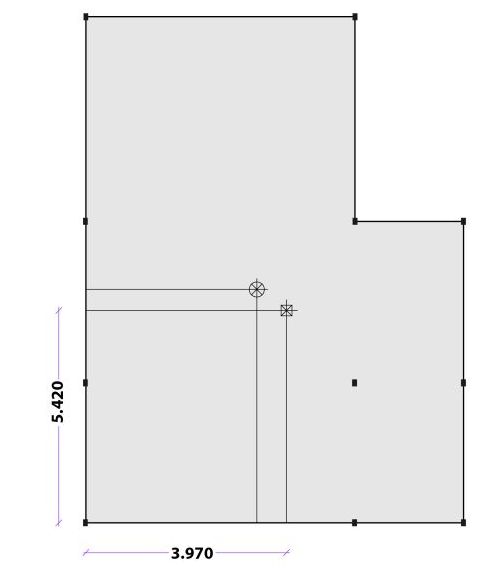
Successivamente vengono calcolate le coordinate del centro di massa, mediante una semplice media ponderata che considera la posizione del baricentro e l’area di ognuna delle figure archetipe in cui la pianta è suddivisa.

Il calcolo della posizione del centro delle rigidezze dipende dalla rigidezza dei singoli telai e dalla loro posizione rispetto all’origine. Una seconda media ponderata, che tiene conto della rigidezza totale lungo i 2 assi cartesiani di riferimento.

La sommatoria del prodotto tra la rigidezza di ogni telaio e il quadrato della sua distanza dal centro delle rigidezze porta al valore della rigidezza rotazionale. A parità di rigidezza infatti maggiore è la distanza che il telaio ha rispetto al centro delle rigidezze e maggiore è il contributo che fornisce nella limitazione degli spostamenti.

L’analisi dei carichi è necessaria per determinare la forza sismica che agisce sulla struttura. Infatti come è noto sono le strutture pesanti a soffrire di più i sismi. I carichi al metro quadro dei pesi permanenti e accidentali, moltiplicati per l’area dell’impalcato, per il coefficiente di contemporaneità e successivamente divisi per il coefficiente di intensità sismica portano al valore della forza sismica orizzontale.

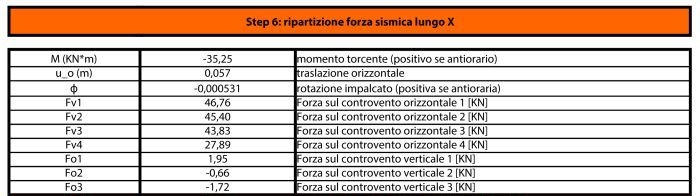
L’ultimo passo consiste nel ricavare la forza che si ripartisce sui singoli telai. La forza sismica orizzontale è applicata sul centro delle masse, generando una traslazione dell’impalcato nella sua direzione: essa si determina dividendo la forza per la rigidezza nella direzione corrispondente. Ma la non coincidenza del centro delle masse con il centro delle rigidezze provoca anche una rotazione dell’impalcato, per via del momento torcente che in questo modo si genera, che dipende proprio dal prodotto tra la forza orizzontale equivalente e la differenza tra le ascisse e le ordinate dei 2 centri (che quindi portano ad avere 2 valori di momenti torcenti).

L’entità della rotazione dell’impalcato si ottiene dividendo i momenti torcenti per la rigidezza rotazionale. Queste 2 grandezze sono dimensionalmente coerenti, infatti la rotazione è adimensionale.

Grazie ai dati ottenuti è possibile calcolare la forza orizzontale che ogni telaio sarà chiamato a controventare. Nell’esempio preso in considerazione essa è per la maggior parte dovuta allo spostamento e in minima parte alla rotazione, per via dell’enorme differenza che sussiste tra la rigidezza rotazionale e quelle di traslazione (tra le 20 e le 40 volte più piccola) e del valore del momento torcente, che è solo la metà della forza sismica orizzontale.