Esercitazione 8 - GRATICCIO DI TRAVI

Un graticcio di travi è definibile tale quando non vi è una gerarchia strutturale tra le travi; non essendoci travi primarie e secondarie le travi avranno tutte la stessa sezione, così come i momenti di inerzia saranno simili nelle due direzioni.

Sfrutteremo questo esercizio per analizzare il problema della TORSIONE, generata proprio dalla stretta collaborazione tra le travi che compongono il graticcio.

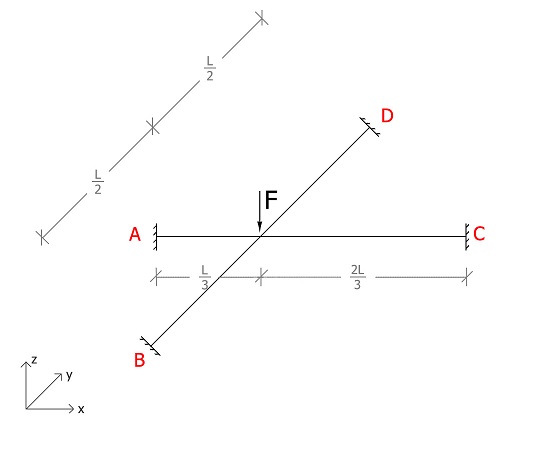
Svolgiamo questo esercizio con la SOVRAPPOSIZIONE DEGLI EFFETTI, analizzando la trave AC e la trave BD separatamente.

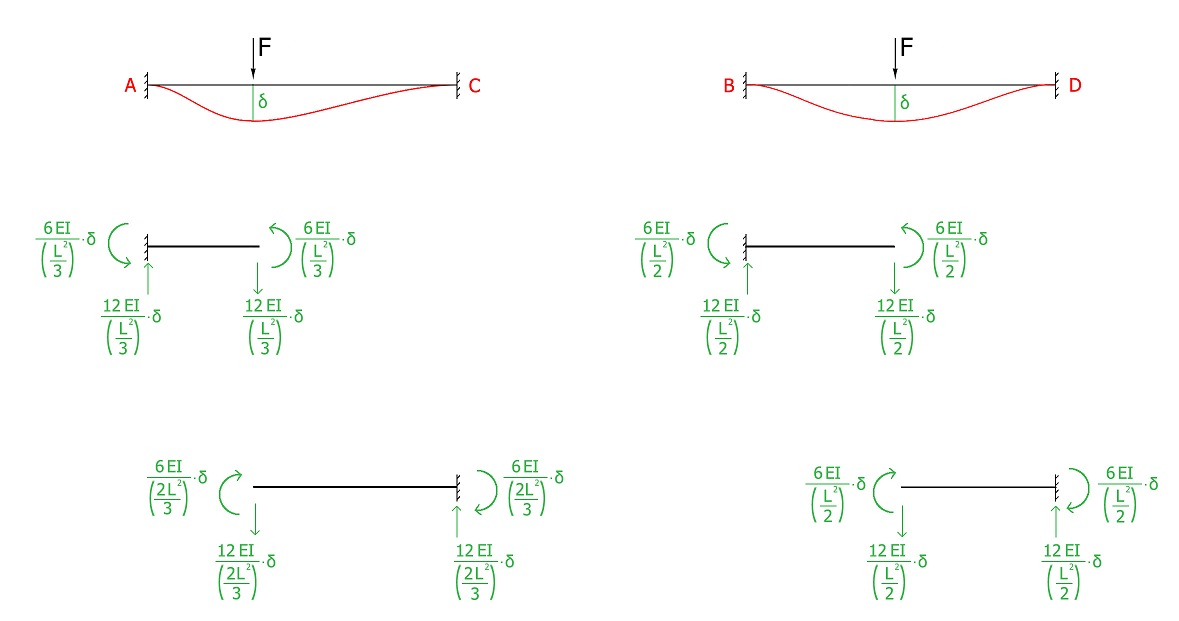
1) ANALISI DELLE DEFORMATE DOVUTE ALLO SPOSTAMENTO δ

Tale spostamento lo vedo come un cedimento vincolare che "separa in due ogni singola trave"

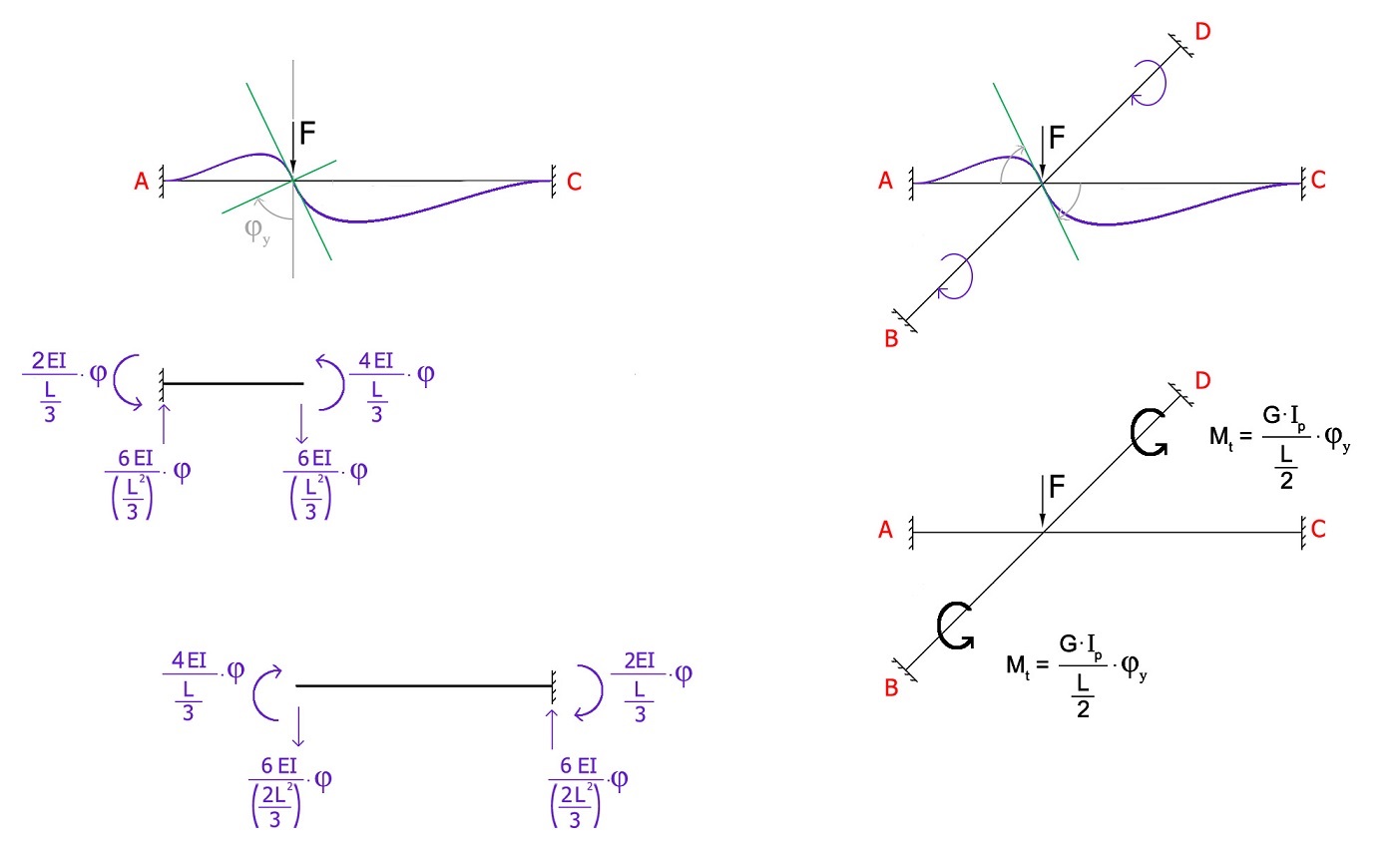
2) ANALISI DEGLI EFFETTI DOVUTI ALLA ROTAZIONE φ

La rotazione φ_y diventa TORSIONE per l'altra asta; si attivano quindi i M_t che si oppongono alla torsione.

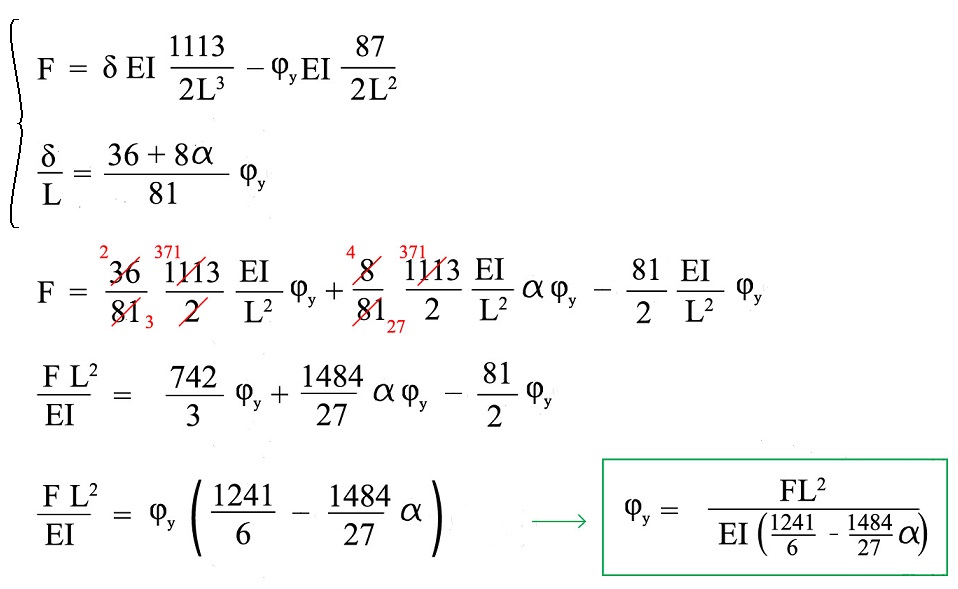
3) STUDIO DEI TAGLI

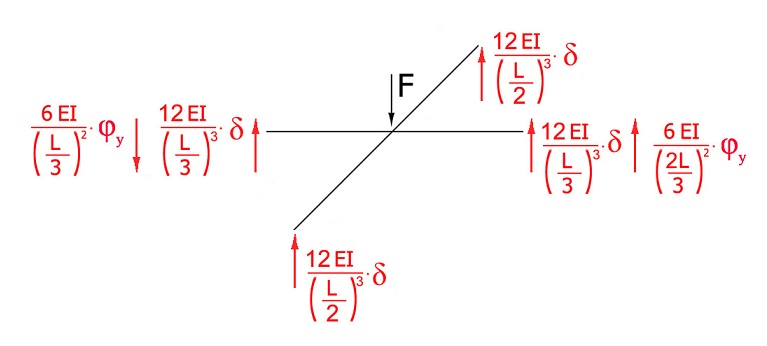
Scrivo l'equazione:

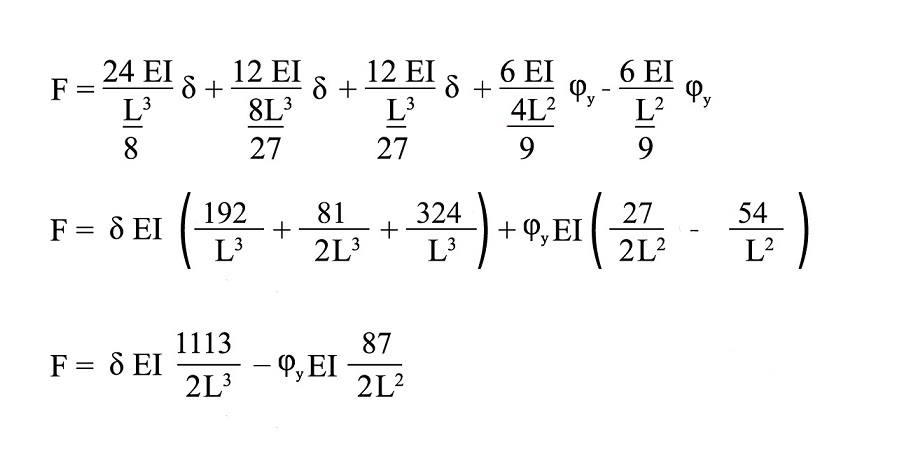
4) STUDIO DEI MOMENTI

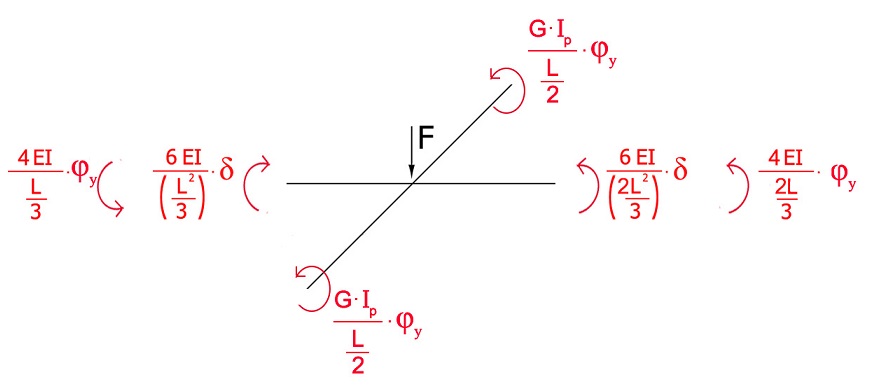
Scrivo l'equazione:

E quindi: