Esercitazione: Graticcio di Travi

Inviato da niccolò.canulli il Mer, 18/09/2013 - 23:46

Graticcio di Travi

Un graticcio, al contrario di una gerarchia, è un modello composto da un sistema di travi ortogonali che collaborano tra loro reciprocamente.

Un parametro importante in un graticcio è la rigidezza torsionale (GJp/l) poichè la flessione in una direzione provoca inevitabilmente la torsione nella sua corrispettiva ortogonale.
Il termine Ip si riferisce al momento d'inerzia polare che varia a secondo della sezione presa in esame.

Mt = (GIp/l)ϕ

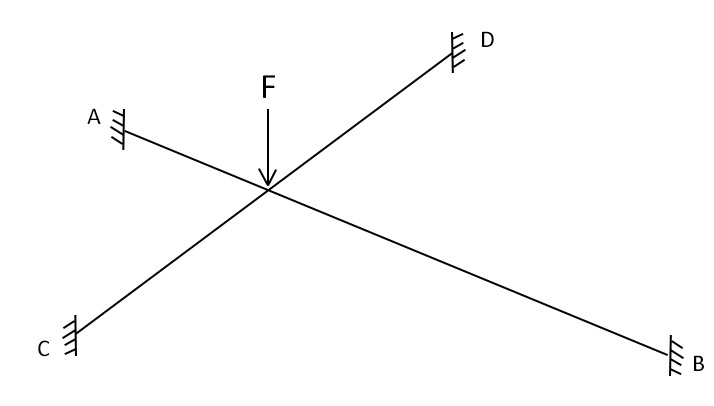
Il nodo ha 6 gradi di libertà: 3 traslazioni lungo i tre assi e 3 rotazioni intorno ai tre assi
In questo caso specifico avremo un abbassamento delle due travi che provocherà una rotazione nelle sezioni della trave AB che a sua volta provocherà una torsione della trave CD

Andiamo ad analizzare i due abbassamenti:

AB:

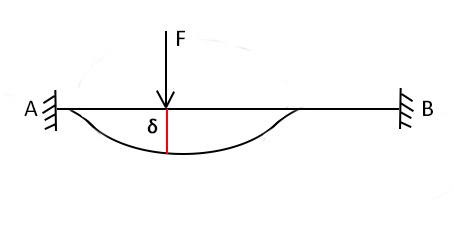
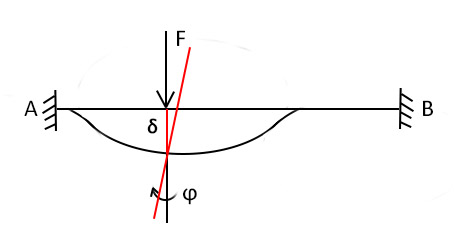
La forza F produce un abbassamento ᵟ della trave, conoscendo già i valori della rigidezza di una trave doppiamente appoggiata potremo ricavare gli sforzi di Taglio e Momento:

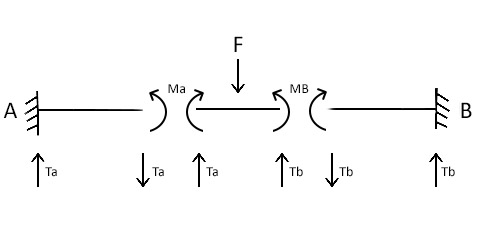
TAGLIO:  T= (12EJ/l3) ϭ              Ta= (324EJ/l3) ϭ               Tb= (81EJ/2l3) ϭ

MOMENTO: M= (6EJ/l2) ϭ              Ma= (54EJ/l2) ϭ               Mb= (27EJ/2l2) ϭ

BC:

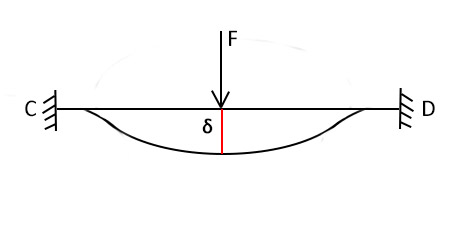
Anche il nodo dell'asta CD, sotto il carico della forza F si abbassa senza ruotare:

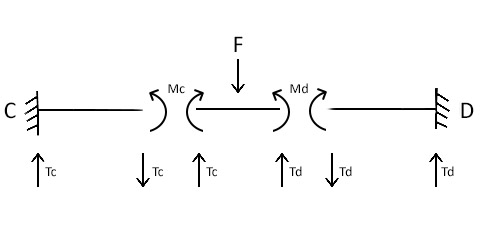
TAGLIO:  T= (12EJ/l3) ϭ              Tc= (96EJ/l3) ϭ               Td= (96EJ/l3) ϭ

MOMENTO: M= (6EJ/l2) ϭ              Mc= (24EJ/l2) ϭ               Md= (24EJ/l2) ϭ

Ora andiamo ad analizzare la rotazione della sezione della trave AB:


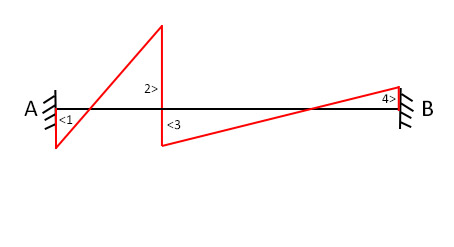
Possiamo inserire i classici schemi notevoli già ricavati dalla questione della rigidezza flessionale per ricavare i momenti della trave:

 

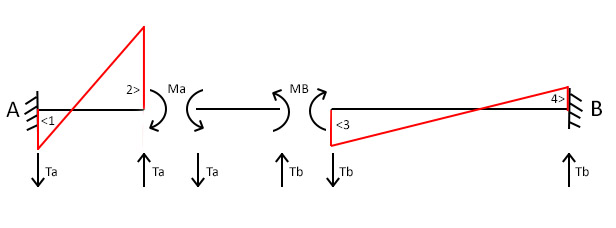
MOMENTO: M= (4EJ/l) ϕ                 M= (2EJ/l) ϕ               

                  M1= (6EJ/l) ϕ               M2=Ma= (12EJ/l) ϕ

                  M3=Mb= (6EJ/l) ϕ         M4= (3EJ/l) ϕ

TAGLIO:     Ta= (54EJ/l2) ϭ             Tb= (27EJ/2l2) ϕLa rotazione della trave AB provoca una torsione della trave CD:


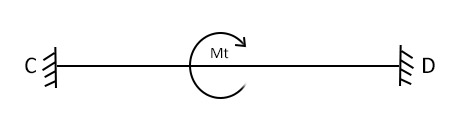
Il valore del momento torcente sarà:  (2GJp/l) ϕ

Conoscendo tutti i contributi degli sforzi di Taglio e Momento che agiscono sul nodo potremmo scrivere le due equazioni di equilibrio:

traslazione verticale:   ΣFz = 0     F= Taϭ- Taϕ+ Tcϭ+ Tbϭ+ Tbϕ+ Tdϭ          F= (1113EJ/2l3)ϭ- (81EJ/2l2)ϕ

equilibrio dei momenti:  ΣMy = 0     0=- Maϭ- Mbϭ + M2ϕ+ M3ϕ+ Mtϕ + Mtϕ          ϭ/2= ϕ[(38+8α)/81]

Sostituiamo ϭ/2 all'interno della prima equazione per trovare l'incognita rotazionale ϕ:

ϕ = Fl2 / [EJ((1231/6)+(1484/27)α)]