ESERCITAZIONE 1 / PARTE 1

TRAVE RETICOLARE ISOSTATICA BIDIMENSIONALE

Questa esercitazione tratta delle strutture reticolari. In questa prima fase studierò una trave reticolare bidimensionale isostatica, dalle reazioni vincolari alle caratteristiche della sollecitazione attraverso il metodo delle sezioni di Ritter.
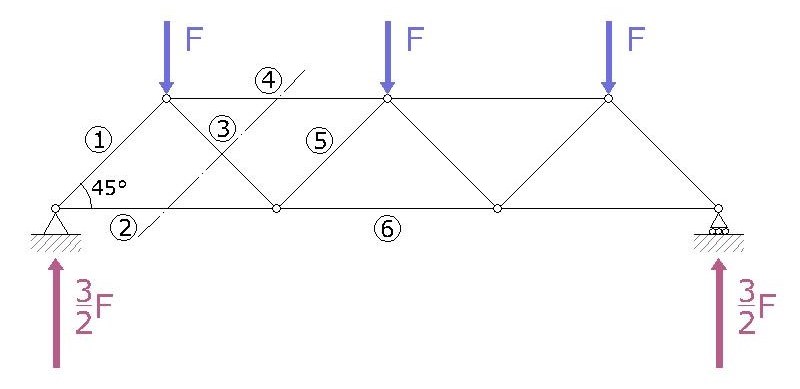
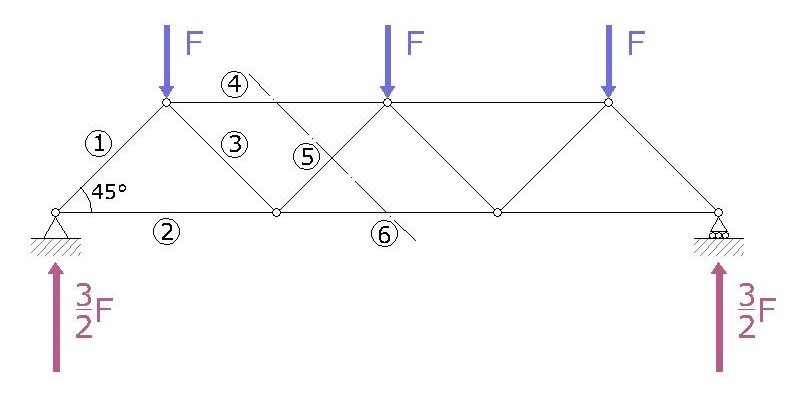
La trave che prendo in esame è costituita da tre campate di 6m di base per 3 m di altezza per la lunghezza totale di 18 m. Per semplificare i calcoli utilizziamo la lunghezza L di riferimento con L=3m. Come tutte le travi reticolari gli elementi che la compongono sono collegati tra essi tramite una cerniera interna. Ho applicato poi una cerniera esterna sul punto A mentre un carrello esterno sul punto H. I carichi concentrati vengono applicati sui nodi nei punti B, D e G. In questo caso ho messo tre carichi verticali pari a F diretti verso il basso.

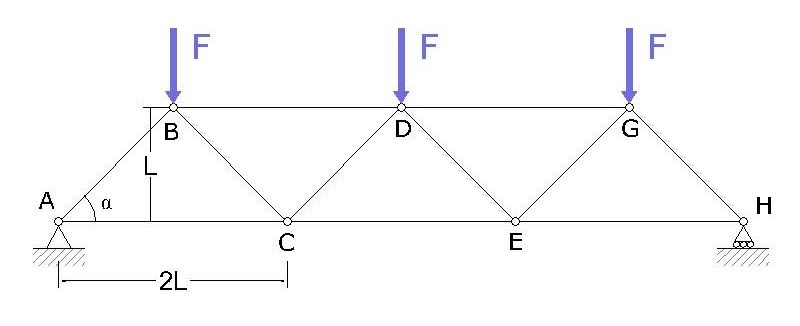
REAZIONI VINCOLARI

La soluzione delle reazioni vincolari è piuttosto veloce se si considera che la trave ha una configurazione geometrica simmetrica ed è caricata simmetricamente. Dunque il carico totale 3F sarà diviso in parti uguali nelle reazioni vincolari pertanto avremo 3/2 L verso l'alto sia in A che in H.

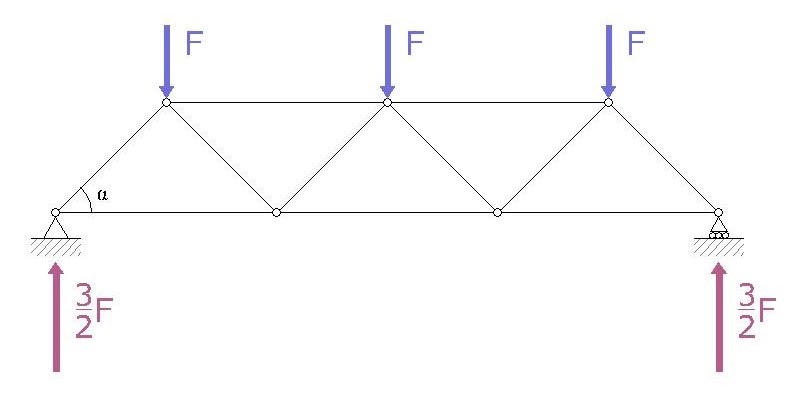
CARATTERISTICHE DELLA SOLLACITAZIONE

Cominciamo con lo studio delle caratteristiche della sollecitazione attraverso il metodo delle sezioni di Ritter sapendo che consideriamo il peso strutturale trascurabile e quindi nullo e che nelle travi reticolari caricate sui nodi le sollecitazione delle aste sono tutte parallele alle direzioni delle aste a cui appartengono e cioè sono normali alla sezione trasversale quindi avremo solo elementi compressi o tesi. inoltre posso analizzare anche solo metà delle aste in quanto, come detto in precedenza, la struttura è simmetrica e simmetricamente caricata pertanto anche le sollecitazioni sono simmetriche.

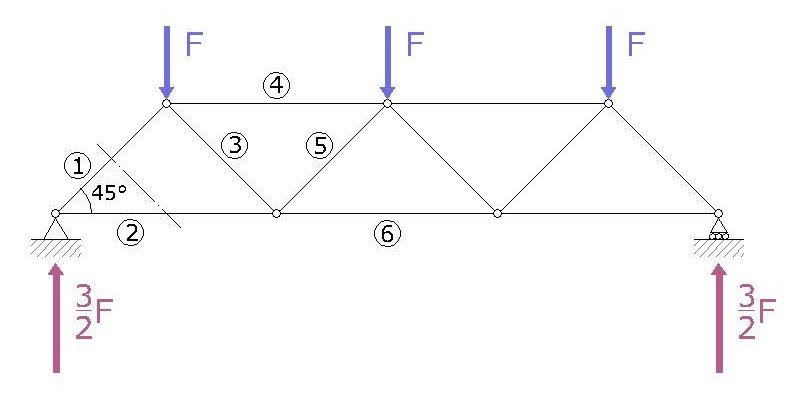
La prima sezione la eseguiamo sulle aste 1 e 2.

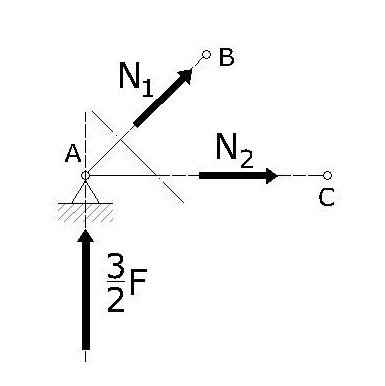
Visto che le forze in giuoco sono solo tre allora possiamo pensare di risolvere facilmente il sistema con il metodo grafico. Infatti le tre rette d'azione creano un triangolo rettangolo in cui due lati formano un angolo di 45 gradi: è un triangolo isoscele e conosciamo un cateto, visto che è la reazione vincolare 3/2 F, sappiamo immediatamente quale è il valore dell'altro cateto. L'ipotenusa la troviamo facilmente in quanto è un cateto moltiplicato per la radice di due.

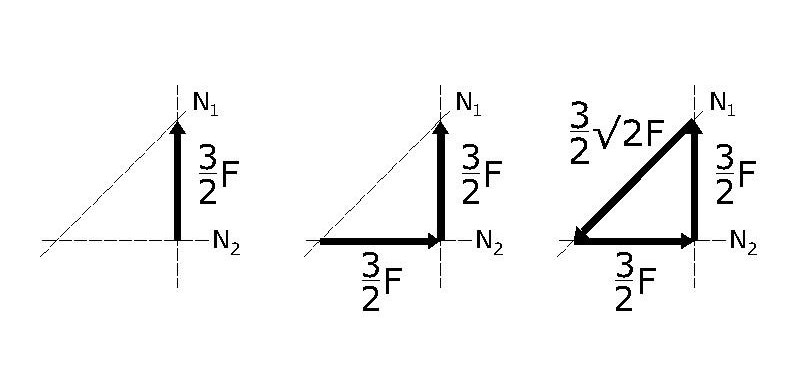
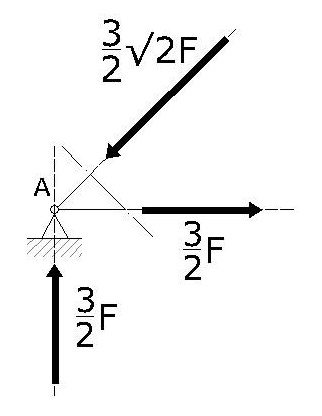
Possiamo osservare che l'asta 1 è compressa, quindi è un puntone, mentre la 2 è tesa, quindi è un tirante.

Ora faccio una sezione che intersechi le aste 2, 3 e 4.

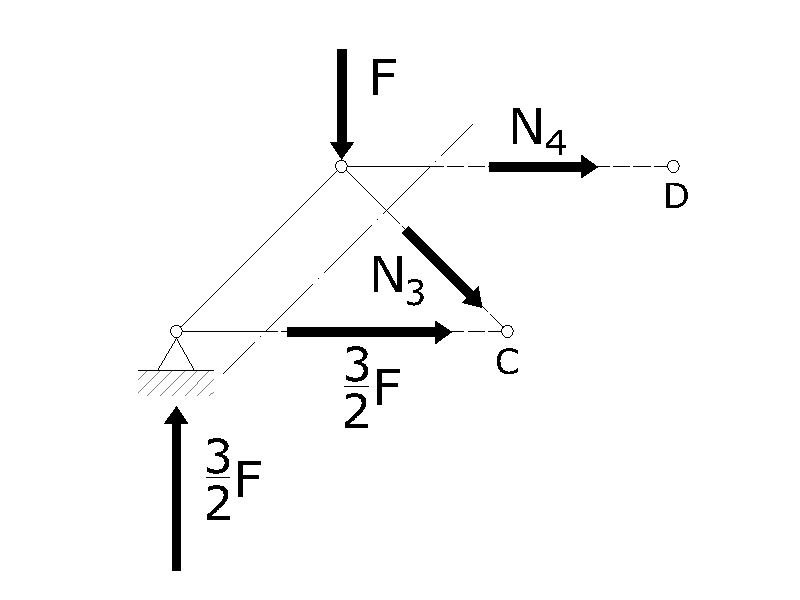
Questa volta lo schema non è semplice come quello della sezione precedente, la strada più semplice per la soluzione è quella che prevede l'utilizzo di equazioni di equilibrio alla rotazione che annullino di volta in volta una incognita e magari qualche altra forza nota al fine di semplificare i calcoli. Iniziamo con l'equazione dell'equilibrio alla rotazione calcolata nel punto C per trovare la sollecitazione dell'asta 4

-3/2F·2L+F·L-N₄·L=0
N₄=-2L

Il segno negativo di N4 ci informa del fatto che abbiamo sbagliato il verso ipetetico della forza quindi la è entrante anziché uscente.

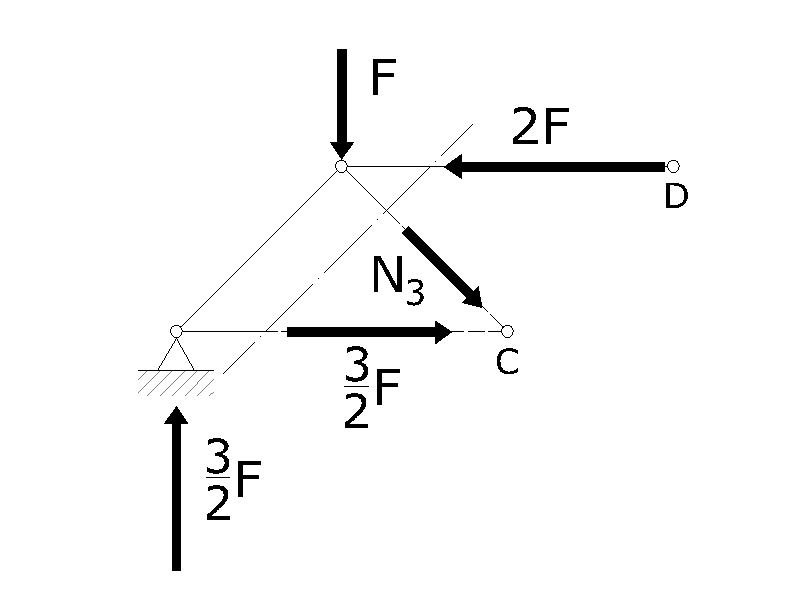
Per scoprire quale è il valore di N₃ facciamo la rotazione all'equilibrio nel punto A

-F·L+2F·L-N₃·√2L=0
N₃=√2/2·F

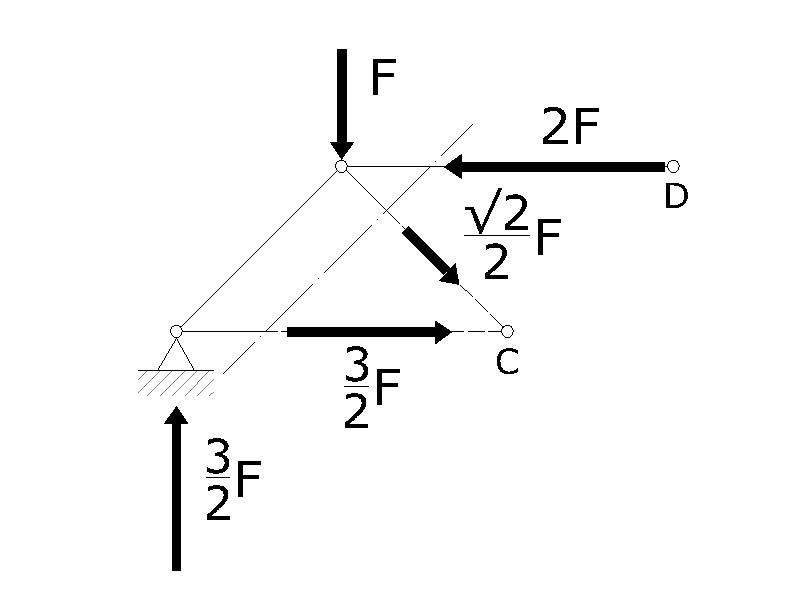
Rimane una ultima sezione e più precisamente quella che interseca le aste 4, 5, e 6.
 

Come con la sezione precedente per scoprire il valore di N₅ e N₆ utilizziamo le equazioni ni equilibrio alla rotazione.
Iniziamo con l'equazione di equilibrio alla rotazione sul punto D per trovare N₆.

-3/2·3L+F·2L+N₆·L=0
N₆=5/2·F

Ora con l'equazione di equilibrio alla rotazione sul punto A troviamo N₅.

-F·L+2F·L+N₅·√2L=0
N₅=-√2/2·F

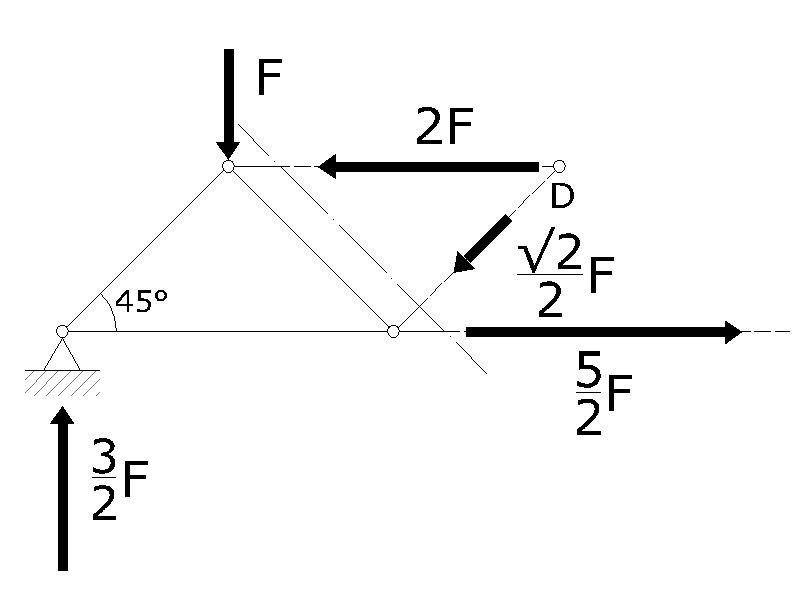
Adesso sono note tutte le caratteristiche della sollecitazione e posso disegnare il diagramma nelle normali.

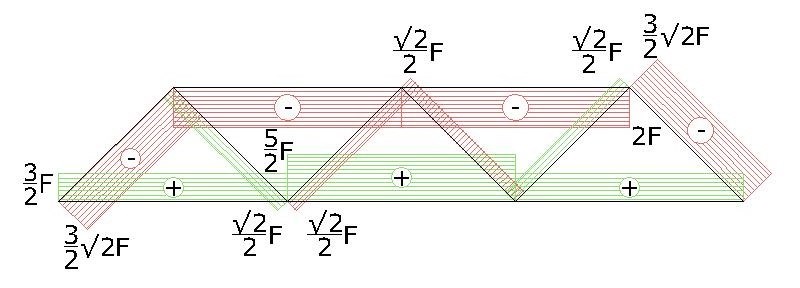
Come è possibile osservere le aste più sollecitate sono quelle ai bordi del sistema e più in specifico sono il puntone diagonale adiacente al vincolo (3/2·F) e il tirante centrale (√2/2·F).

La successiva fase è il controllo della trave reticolare attraverso il software SAP2000. Per rendere confrontabili i risultati devo però attribuire a F un valore in termini fisici. Immagino che la struttura reticolare sia adibita a copertura non praticabile e, ignorando i carichi strutturali della struttura e i sovraccarichi permanenti, applico solo i sovraccarichi accidentali che sono tabellati dalle NTC D.M. 14 gennaio 2008 cioè F=1,2 kN

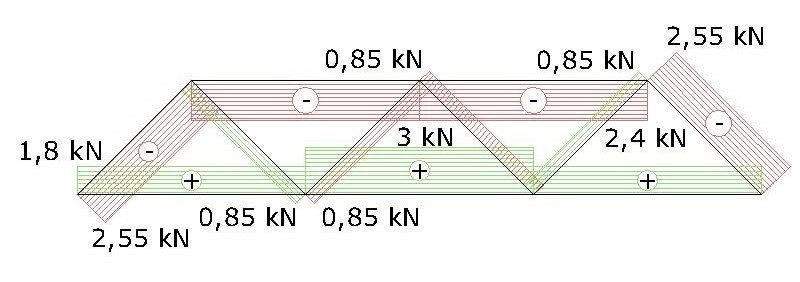
Malgrado il tirante centrale sia il più sollecitato, non necessariamente sarà il tratto con una sezione dimensionalmente più grande. La trave 4 e la corrispondente simmetrica ( ma in generale tutte le travi compresse) devono infatti dare conto del carico di punta ovveroquel caso in cui la sezione resistente rispetto alla lunghezza della trave risulti snella. Nel tal caso anche a parità di superficie resistente, la trave dovrà avere un ingombro maggiore.

A breve la seconda parte che tratterà della trave reticolare bidimensianle sul software SAP2000.