blog di Ottavio Minella

Per questa esercitazione abbiamo preso in oggetto una porzione dell'edificio progettato per  il corso di progettazione architettonica lm2. Questo fabbricato è pensato per essere realizzato con struttura in acciaio e quindi con i conseguenti controventi. Siamo partiti dal predimensionamento degli elemnti strutturali, alla definizione del centro delle rigidezze e al calcolo delle forze sismiche. Abbiamo calcolato gli spostamenti e rotazioni confrontandoli con i risultati del software SAP200 constatando la corrispondenza degli stessi.

In allegato l'esercitazione per esteso.

Questa esercitazione tratta del dimensionamento delle travi a mensola di una struttura isostatica realizzata con le tre tecnologie tradizionali: legno acciaio e calcestruzzo armato. Per il calcolo dei carichi strutturali permanenti e accidentali faccio riferimento a ”Esercitazione 2 – Dimensionamento travi” nella quale per le stesse tipologie costruttive veniva però è dimensionato il sistema di travi doppiamente appoggiate. Per il dimensionamento utilizzo una foglio Excel appositamente preparato.

Disegno la struttura che voglio prendere in considerazione,  e sarà sempre la stessa per le tre tecnologie, indico con i numeri le travi per riferirle nei fogli Excel e determino le aree di influenza.

LEGNO

Comincio inserendo nelle tabelle i valori dei carichi già calcolati nella precedente esercitazione e le dimensione dell’attuale progetto. Le tabelle daranno già il valore di q e del momento flettente massimo.

Ora devo  scegliere il legname della trave. Opto per un legno lamellare GL 24 h che ha una resistenza alla flessione di 24 N/mmq per un modulo di elasticità pari a 11600 MPa. Il valore kmod dipende dalla classe d’uso della trave o meglio in quali condizioni di carico e umidità verrà utilizzata la struttura. Per il nostro caso va bene 0,8. Questo coefficiente serve a ridurre la resistenza certificata in modo da calcolare l’aggravio delle condizioni esterne di esercizio.

Fisso la base a 30 cm e ottengo  l’altezza minima che serve alla trave per superare senza rompersi quella luce. L’altezza così ottenuta deve essere aumentata per considerare il peso proprio della trave che solo in questa fase possiamo calcolare e anche un fattore di ingegnerizzazione. Inserisco il peso specifico del legno che abbiamo scelto (3,8 kN/mc) e aumento  l’altezza finche la trave non sarà verificata cioè fino a quando la tensione di verifica sarà minore della tensione ammissibile. 

Fatta la verifica a resistenza deve essere fatta anche quella alla deformabilità. Per ottenerla devo inserire il modulo di elasticità del legno scelto.

Noto che, nonostante la verifica a resistenza sia stata superata, quella alla deformata in alcuni casi non è stata soddisfatta. Per adeguare la trave quindi devo continuare ad aumentare il valore dell’altezza finché non ottengo la verifica.

ACCIAIO

Anche qui inserisco i valori dei carichi e le dimensioni di progetto di interasse e luce.

Come già abbiamo osservato nel dimensionamento con il legno la mensola più sollecitata è la 3. Quest’ultima ha infatti un’area di influenza più alta rispetto alle altre travi. A questo punto scelgo  la classe di acciaio per definire quale è la resistenza ammissibile. In questo caso utilizziamo quello indicato con la sigla S275 e ha una tensione di crisi pari a 275 MPa.

Ora devo ricorrere al profilario per vedere quali sono i profili commerciali che superano il modulo di resistenza di progetto. Allo stesso tempo posso verificare se questo è sufficiente grande da sostenere anche il proprio peso visto che fino a questo momento non era stato considerato.

La verifica non è ancora conclusa. Infatti a deformabilità la mensola 1 supera l’abbassamento consentito

Quindi ora aumento la sezione finché non viene soddisfatta anche questa verifica.

CALCESTRUZZO ARMATO

Come per gli altri due materiali inserisco i carichi e i valori dimensionali di interasse e luce delle mensole quindi devo scegliere le classi di resistenza del calcestruzzo e dell’acciaio. Per il calcestruzzo opto per uno C32/40 con una resistenza a compressione di 40 MPa (N/mmq); la scelta dell’acciaio è condizionata dalla normativa, nel senso che se ci troviamo in zona sismica (come effettivamente lo è la maggior parte dell’Italia) posso  scegliere un acciaio più duttile quindi il B450C con 450 MPa di tensione a snervamento. Inseriamo anche questi dati nelle caselle apposite.

Immagino dei pilastri  quadrati 30 cm quindi fisso la base della trave a 25 cm e un delta classico a 5 cm. L’algoritmo programmato darà come risultato l’altezza al netto del copriferro. Quello che devo  fare ora è inserire una altezza totale H che sia almeno grande quanto l’altezza appena  calcolata (h) sommata al copriferro (H=h+delta). Nel caso in questa non risulti sufficiente provvedo ad aumentare il valore dell’altezza della trave.

Come di consueto la verifica si conclude sono quando anche la verifica a deformabilità ha avuto successo .

In allegato metto a disposizione il file utòlizzato per questa esercitazione.

Devo risolvere il sistema formato da una trave iperstatica con l’equazione della linea elastica.

 

Prima di fare i calcoli faccio un’analisi qualitativa. Questa mi aiuterà a capire e a controllare i risultati. Incomincio disegnando una ipotetica deformata.

Il sistema ha una spiccata asimmetria. La trave si deforma maggiormente dove è meno rigida, in questo caso in quella parte dove è meno vincolata. Inoltre so che in corrispondenza del vincolo cerniera in B mi aspetto una singolarità. I primi due punti di flesso sono sicuramente all’interno del segmento AB mentre il terzo nel segmento BC, anche se per adesso non so quali siano i punti precisi. I punti di flesso sono quei punti dove la curvatura è nulla e in quei punti certamente anche  il momento è nullo. Per disegnale qualitativamente il diagramma dei momenti quindi mi è rimasto da definire il tipo di funzione ma è facile se osservo il carico costantemente distribuito q2, infatti se q2 è –q il taglio sarà lineare mentre il momento parabolico. In A c’è un incastro e mi aspetto un valore diverso da zero mentre in B in corrispondenza della singolarità mi aspetto una cuspide, infine in C il momento è nullo perché ci troviamo su un vincolo carrello.

A questo punto analizzo il taglio. Come già detto in precedenza il taglio è lineare a ha la stessa inclinazione per tutti i tratti:

- nel tratto BC il punto di nullo è più vicino a C perché il vertice della parabola si trova nello stesso punto

- nel tratto AB il punto di nullo, corrisponde al vertice della parabola del momento ed è evidentemente vicino ad A

So che in B c’è una singolarità quindi devo analizzare la trave con due equazioni differenti. Per non confondermi, utilizzo una nomenclatura univoca per indicare gli elementi nel modo più preciso possibile. Quindi utilizzo il pedice 1 e le costanti di integrazione C per tutti gli elementi che si trovano nel tratto AB e il pedice 2 e le constanti di integrazioni D per tutti gli elementi che si trovano sul tratto BC.

L’equazione della linea elastica per il tratto 1 è:

Di conseguenza l’equazione dello spostamento è:

L’equazione della linea elastica per il tratto 1 è:

Di conseguenza l’equazione dello spostamento è

Ora definisco le condizioni al contorno si cinematiche che statiche

A             nell’incastro vengono impedite le traslazioni assolute e le rotazioni assolute

B             per questo punto devo fare un ragionamento più complesso perché devo capire la relazione tra le due parti della trave e il significato meccanico della continuità. Il vincolo cerniera ci dice che gli spostamenti non sono consentiti ma sono consentite le rotazioni. Ma se è vero che il vincolo non blocca le rotazioni assolute, nulla midice sulle rotazioni relative. Queste infatti sono nulle perché la trave è continua e dall’analisi qualitativa del momento ho visto anche che c’è continuità per questa sollecitazione.

C             In questo punto trovo un vincolo carrello, pertanto ho sia una condizione al contorno cinematica sia una condizione al contorno statica:

Prima di scrivere il sistema di otto equazioni e otto incognite che mi permetterà di trovare le costanti di integrazione della linea elastica, provo a determinare e semplificare velocemente costanti ed equazioni

 

 

 

 

Ricapitolando

Quindi posso ridurre il problema in un sistema di cinque equazioni di cinque incognite

 

 

Adesso procedo con la risoluzione delle equazioni

 

 

 

 

Ora prendo in esame le ultime due per trovare D3 in funzione di D2

 

 

Adesso prendo in esame le prime tre

 

 

Attraverso più facili sostituzioni trovo che:

 

 

Quindi riscrivo le equazioni sostituendo le costanti di integrazione

 

 

Tramite queste equazioni riuscirò a capire come funziona per intero la struttura. Comincio con Taglio e Momento del tratto 1

 

 

E vedo dove si annulla per sapere dove si trova il vertice della parabola del Momento:

 

 

Come ipotizzato all’inizio, il vertice della parabola si trova più vicino ad A. Per il Momento otterrò:

 

Ripeto i calcoli fatti per il tratto 1 sul tratto 2

 

 

E vedo dove si annulla per sapere dove si trova il vertice della parabola:

Di nuovo viene confermata l’ipotesi iniziale della posizione del vertice della parabola cioè più vicina al punto C. Ora calcolo il Momento sapendo però che è dato dalle condizioni al contorno:

Disegno i diagrammi delle sollecitazioni dai quali evincerò le reazioni vincolari.

 

 

 

ESERCITAZIONE 2 – Dimensionamento Travi

Questa esercitazione tratta del dimensionamento delle travi di una struttura realizzata di volta in volta con materiali differenti:

-          Legno

-          Acciaio

-          Calcestruzzo armato

In coerenza al materiale cambierà la tecnologia dei solai e il calcolo delle dimensioni delle travi.

LA SRTUTTURA

La struttura presa in esame è semplice. Immaginiamo infatti che sia un piano di un edificio destinato a civile abitazione in cui le travi sono isostatiche cioè hanno una cerniera e un carrello ai loro estremi. Proviamo a disegnare una planimetria strutturale.

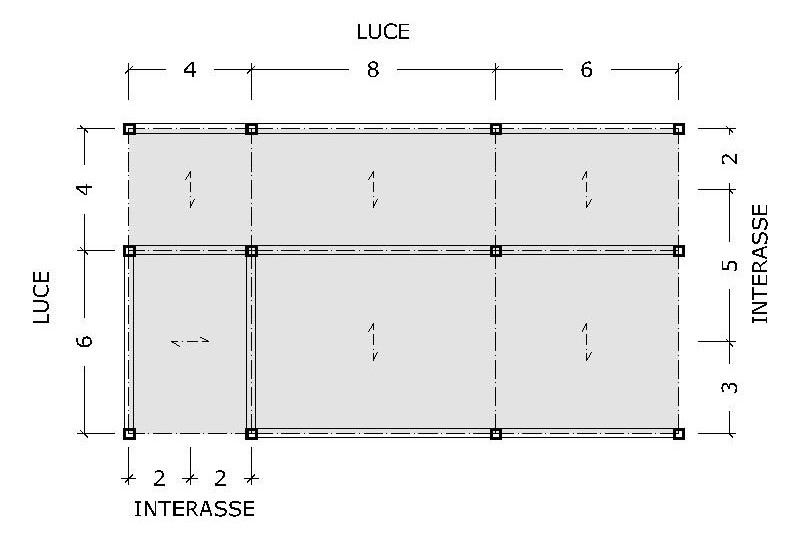
E successivamente proviamo a vedere quali sono le aree di influenza per ciascuna trave.

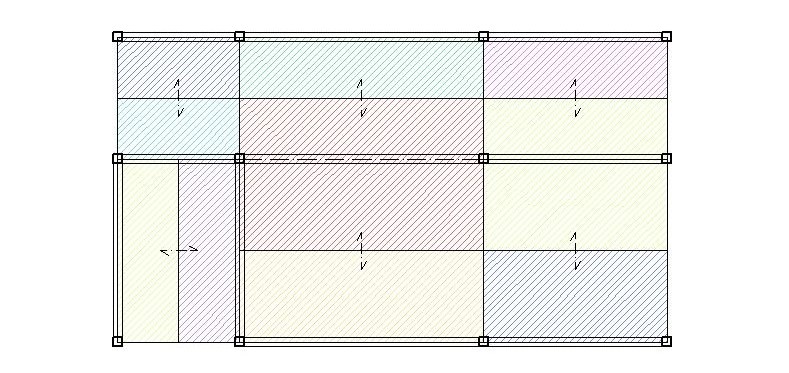
Ora assegniamo per ugni trave un numero che ci aiuterà ad identificarla univocamente.

 

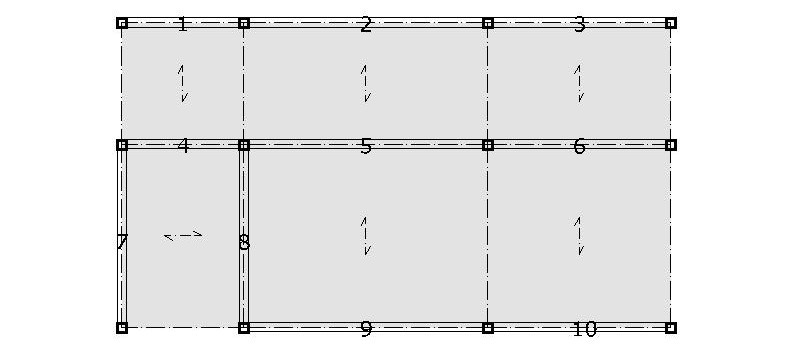
È possibile osservare che la trave 5 è quella che ha più area di influenza ci aspettiamo quindi che sia quella più caricata. Con il foglio Exel noi però abbiamo la possibilità di calcolarci velocemente tutte le travi. In ottica di una ottimizzazione dei materiali possiamo calcolare tutte le travi princiapali.

LEGNO

Il primo materiale che calcoleremo è il legno. Coerentemente a questo materiale per la trave associamo un solaio in legno di tipo tradizione.

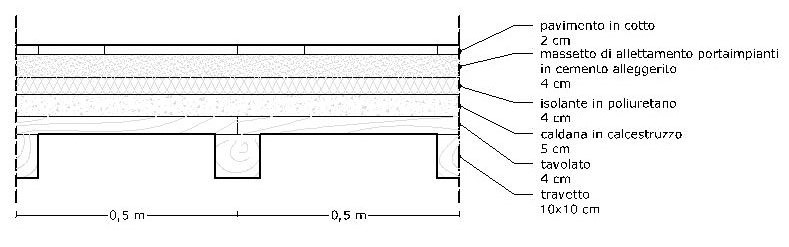
Analizziamo quindi il carico sull’unità di superficie che questo solaio trasmette alle travi per le relative aree di azione.

CARICO STRUTTURALE (qs)

In questa categoria per ora non possiamo mettere la trave principale perché ancora le sue dimensioni sono incognite, ma inseriamo in peso dei travetti in castagno.

Peso specifico legno = 7 kN/mc
Volume travetto = (0,1 m x 0,1 mq x 1 m) : 1mq = 0,01 mc/mq
Volume totale= 0,01 mc/mq x 2 = 0,02 mc/mq
qs = Volume totale x Peso specifico = 0,02 mc/mq x 7 kN/mc = 0,14 kN/mq
qs= 0,14 kN/mq

CARICO PERMANENTE (qp)

Sono tutti quei carichi che non fanno parte della struttura ma che graveranno in modo permanentemente su di essa.

Tavolato in legno di castagno

Peso specifico legno = 7 kN/mc
Volume tavolato = (0,04 m x 1 m x 1 m)/mq = 0,04 mc/mq
qp = Volume tavolato x Peso specifico = 0,04 mc/mq x 7 kN/mc = 0,28 kN/mq
qp= 0,28 kN/mq

Caldana in calcestruzzo

Peso specifico calcestruzzo = 21 kN/mc
Volume caldana = (0,05 m x 1 m x 1 m)/mq = 0,05 mc/mq
qp = Volume caldana x Peso specifico = 0,05 mc/mq x 21 kN/mc = 1,05 kN/mq
qp= 1,05 kN/mq

Isolante in poliuretano estruso

Peso specifico poliuretano = 0,35 kN/mc
Volume isolante = (0,04 m x 1 m x 1 m)/mq = 0,04 mc/mq
qp = Volume isolante x Peso specifico = 0,04 mc/mq x 0,35 kN/mc = 0,14 kN/mq
qp= 0,14 kN/mq

Massetto di allettamento alleggerito con perle di poliuretano

Peso specifico massetto = 3 kN/mc
Volume massetto = (0,04 m x 1 m x 1 m)/mq = 0,04 mc
qp = Volume isolante x Peso specifico = 0,04 mc x 3 kN/mc = 0,12 kN/mq
qp= 0,12 kN/mq

Pavimento in cotto

Peso specifico laterizio pieno = 18 kN/mc
Volume pavimento = (0,02 m x 1 m x 1 m)/mq = 0,02 mc/mq
qp = Volume isolante x Peso specifico = 0,02 mc/mq x 18 kN/mc = 0,36 kN/mq
qp= 0,36 kN/mq

Divisori

L’influenza dei divisori è stabilita per legge a qp = 1 kN/mq

Impianti

Come per i divisori anche il carico permanete degli impianti è stabilito per legge a qp = 0,5 kN/mq.

qp totale = 3,45 kN/mq

CARICO ACCIDENTALE (qa)

Il carico accidentale è quello che dipende dalla destinazione d’uso dell’edificio. Abbiamo detto che la nostra sarà una struttura adibita ad abitazione civile quindi secondo la normativa dobbiamo applicare:
qa = 2,0 kN/mq

Ora andiamo sul foglio Excel precedentemente preparato per inserire i dati che ci interessano cominciando con quelli di progetto e i carichi appena calcolati.

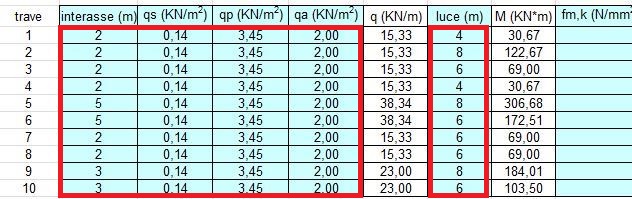
Notiamo innanzitutto che la trave 5 è quella che è più sollecitata quindi ci aspetteremo una sezione maggiore rispetto alle altre. Ora dobbiamo scegliere il legname della trave. Optiamo per un legno lamellare GL 24 h che ha una resistenza alla flessione di 24 N/mmq

Il valore kmod dipende dalla classe d’uso della trave o meglio in quali condizioni di carico e umidità verrà utilizzata la struttura. Per il nostro caso va bene 0,8. Questo coefficiente serve a ridurre la resistenza certificata in modo da calcolare l’aggravio delle condizioni esterne di esercizio.

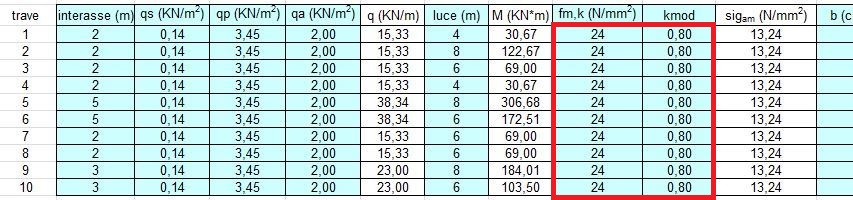
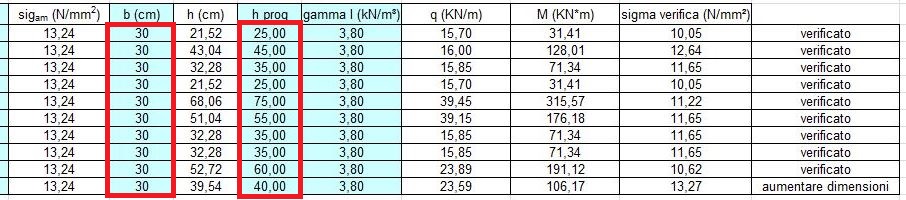
Fissiamo la base a 30 cm e otteniamo l’altezza che serve alla trave per superare quella luce. L’altezza così ottenuta deve essere aumentata per considerare il peso proprio della trave che solo in questa fase possiamo calcolare. Inseriamo il peso specifico del legno che abbiamo scelto (3,8 kN/mc) e aumenteremo l’altezza finche la trave non sarà verificata cioè fino a quando la tensione di verifica sarà minore della tensione ammissibile. Per il solo scopo di verificare l’automatismo della verifica ho sottodimensionato l’altezza dell’ultima trave.

ACCIAIO

Per l’acciaio come per il legno utilizziamo una tecnologia costruttiva coerente con il tipo di materiale.

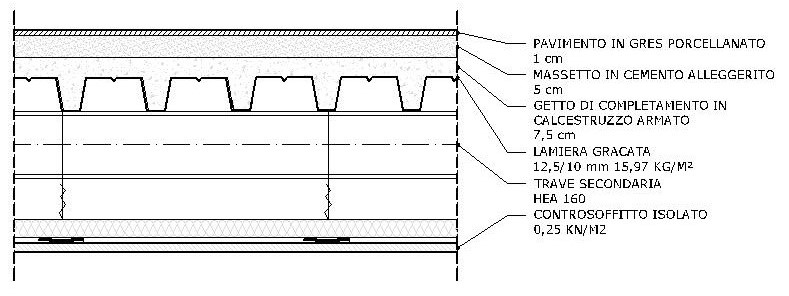
Analizziamo quindi il carico sull’unità di superficie che questo solaio trasmette alle travi per le relative aree di azione.

CARICO STRUTTURALE (qs)

Esattamente come per il legno questo solaio è a doppia orditura, ma nel carico strutturale inseriamo solo quelle che è la travatura secondaria proprio in quanto la principale è incognita

Tipo trave = HEA 160
Peso lineare = 0,3 kN/m
Frequenza  travatura = 1 1/mq
qs = Peso lineare x Frequenza  travatura = 0,02 mc x 7 kN/mc = 0,14 kN/mq
qs= 0,14 kN/mq

CARICO PERMANENTE (qp)

Lamiera grecata ad aderenza migliorata

Il valore del peso della lamiera viene fornita direttamente dal produttore su unità di superficie

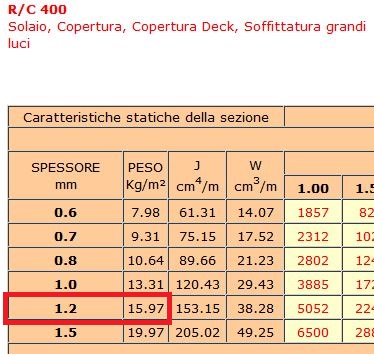
qp= 0,15 kN/mq

Getto di completamento in calcestruzzo armato
per facilitarmi il calcolo dell’area di questo strato l’ho misurata attraverso Autocad

Peso specifico calcestruzzo armato = 25 kN/mc
Volume getto calcestruzzo = (0,064 mq x 1 m)/mq = 0,064 mc/mq
qp = Volume getto calcestruzzo x Peso specifico calcestruzzo = 0,064 mc/mq x 25 kN/mc = 1,65 kN/mq
qp= 1,65 kN/mq

Massetto di allettamento alleggerito con perle di poliuretano

Peso specifico massetto = 3 kN/mc
Volume massetto = (0,05 m x 1 m x 1 m)/mq = 0,05 mc/mq
qp = Volume isolante x Peso specifico = 0,05 mc/mq x 3 kN/mc = 0,15 kN/mq
qp= 0,15 kN/mq

Pavimento in gres porcellanato

Il peso del gres porcellanato viene fornito dal produttore
qp= 0,20 kN/mq

Divisori

L’influenza dei divisori è stabilita per legge a qp = 1 kN/mq

Impianti

Come per i divisori anche il carico permanete degli impianti è stabilito per legge a qp = 0,5 kN/mq

qp totale = 3,65 kN/mq

CARICO ACCIDENTALE (qa)

Come già abbiamo detto l’edificio sarà destinato ad abitazione :
qa = 2,0 kN/mq

Ora andiamo sul foglio Excel precedentemente preparato per inserire i dati che ci interessano cominciando con quelli di progetto e i carichi appena calcolati.

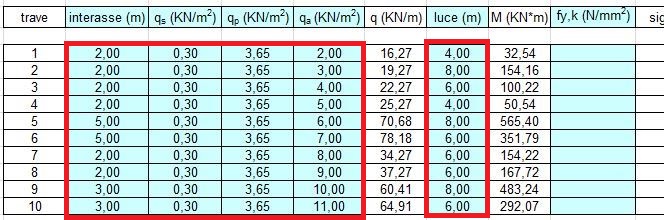
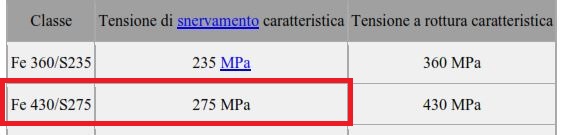
Come già abbiamo osservato nel dimensionamento con il legno la trave più sollecitata è la 5. Quest’ultima ha infatti un’area di influenza più alta rispetto alle altre travi. A questo punto scegliamo la classe di acciaio per definire quale è la resistenza ammissibile. In questo caso utilizziamo quello indicato con la sigla S275 e ha una tensione di crisi pari a 275 MPa

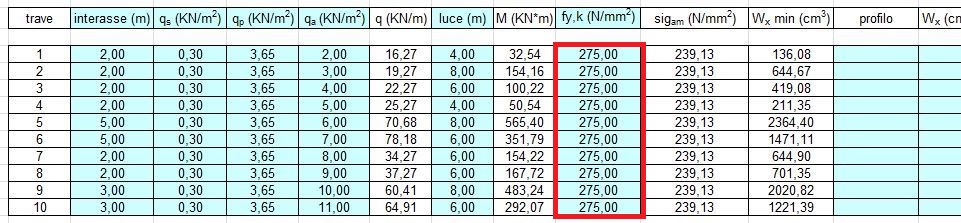
Ora bisogna ricorrere al profilario per vedere quali sono i profili commerciali che superano il modulo di resistenza di progetto. Allo stesso tempo possiamo verificare se questo è sufficiente grande da sostenere anche il proprio peso visto che fino a questo omento non era stato considerato. Il profilo così ottenuto sarà la trave principale di progetto.

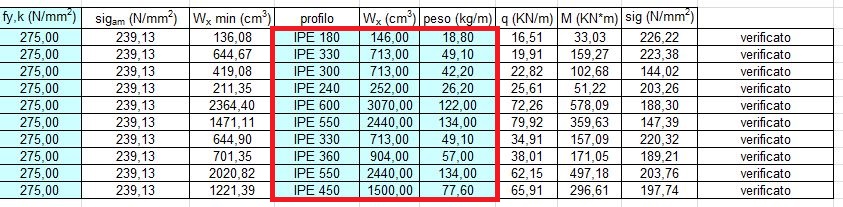
Con la trave 5 siamo riusciti a utilizzare il più grande profil IPE commerciale. Nel caso in cui questo non fosse avvenuto avremmo dovuto scegliere un acciaio ben più resistente.

CALCESTRUZZO ARMATO

Come per le tecnologie precedenti anche qui utilizziamo una tecnologia costruttiva che è coerente con quella della struttura portante principale.

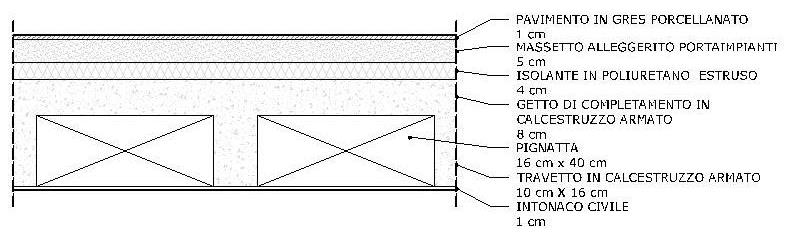
Analizziamo quindi il carico sull’unità di superficie che questo solaio trasmette alle travi per le relative aree di azione

CARICO STRUTTURALE (qs)

La parte struttura di questo solaio corrisponde al getto in calcestruzzo armato che viene colato tra gli elementi di alleggerimento.

Travetti

Peso specifico calcestruzzo = 25 kN/mc
Volume travetto = (0,1 m x 0,16 m x 1 m)/mq = 0,16 mc/mq
Volume totale travetti  = 0,16 mc/mq x 2 = 0,32 mc/mq
qp = Volume getto calcestruzzo x Peso specifico calcestruzzo = 0,32 mc/mq x 25 kN/mc = 8,00 kN/mq
qs= 8,00 kN/mq

Getto di completamento in calcestruzzo armato

Peso specifico calcestruzzo = 25 kN/mc
Volume getto calcestruzzo = (0,08 m x 1 m x 1 m)/mq = 0,08 mc/mq
qp = Volume getto calcestruzzo x Peso specifico calcestruzzo = 0,08 mc x 25 kN/mc = 2,00 kN/mq
qs= 2,00 kN/mq

CARICO PERMANENTE (qp)

Pignatta

Il produttore per una pignatta da 16 x 40 x 25 cm ci fornisce il peso di 0,079 kN
in un mq ci vanno 8 elementi quindi abbiamo un peso totale di:
qp = 8/mq x 0,079 kN = 0,632 kN/mq
 

Isolante in poliuretano estruso

Peso specifico poliuretano = 0,35 kN/mc
Volume isolante = (0,05 m x 1 m x 1 m)/mq = 0,05 mc/mq
qp = Volume isolante x Peso specifico = 0,05 mc/mq x 0,35 kN/mc = 0,0175 kN/mq
qp= 0,14 kN/mq

Massetto di allettamento alleggerito con perle di poliuretano

Peso specifico massetto = 3 kN/mc
Volume massetto = (0,05 m x 1 m x 1 m)/mq = 0,05 mc/mq
qp = Volume isolante x Peso specifico = 0,05 mc/mq x 3 kN/mc = 0,15 kN/mq
qp= 0,15 kN/mq

Pavimento in gres porcellanato

Il peso del gres porcellanato viene fornito dallo stesso produttore
qp= 0,20 kN/mq

Divisori

L’influenza dei divisori è stabilita per legge a qp = 1 kN/mq

Impianti

Come per i divisori anche il carico permanete degli impianti è stabilito per legge a qp = 0,5 kN/mq

qp totale = 1,99 kN/mq

CARICO ACCIDENTALE (qa)

Come già abbiamo detto l’edificio sarà destinato ad abitazione :
qa = 2,0 kN/mq

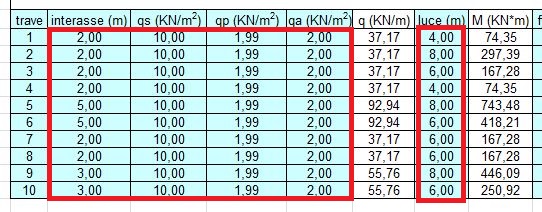
Ora andiamo sul foglio Excel. Come per i materiali precedenti nei carichi strutturali non abbiamo considerato la trave principale quindi una volta dimensionata anche questa va inserita nel calcolo dei carichi esterni e verificata. Ma a differenza dei due materiali precedenti qui ho voluto considerare la verifica della struttura non come la costatazione che la tensione di progetto sia inferiore o uguale a quella ammissibile del materiale ma ho confrontato le altezze delle travi: se l’altezza progettata ha una altezza superiore a quella che risulta dal calcolo con il carico strutturale completo allora posso dire la trave è verificata. È un errore concettuale non di poco conto ma per questa esercitazione non sono previsti i calcoli del dimensionamento dei ferri e quindi diventa impossibile (?) trovare le tensioni di verifica.

Precisato questo andiamo a inserire i dati di progetto e i carichi.

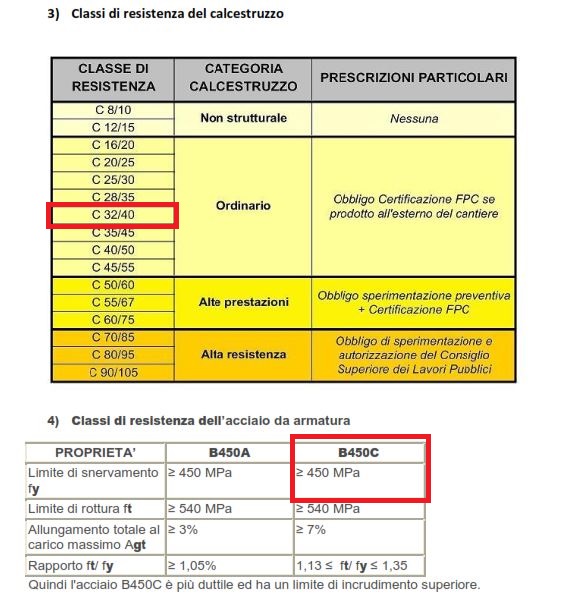
A questo punto bisogna scegliere le classi di resistenza del calcestruzzo e dell’acciaio. Per il calcestruzzo optiamo per uno C32/40 con una resistenza a compressione di40 MPa (N/mmq); la scelta dell’acciaio è condizionata dalla normativa, nel senso che se ci troviamo in zona sismica (come effettivamente lo è la maggior parte dell’Italia) possiamo scegliere un acciaio più duttile quindi il B450C con 450 MPa di tensione a snervamento. Inseriamo questi dati nelle caselle apposite.

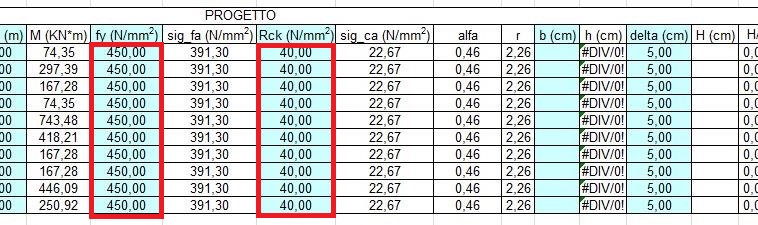
Immaginiamo dei pilastri  quadrati 30 cm quindi fissiamo la base della trave a 25 cm e un delta classico a 5 cm. L’algoritmo programmato darà come risultato l’altezza al netto del copriferro. Quello che dobbiamo fare ora è inserire una altezza totale H che sia almeno grande quanto l’altezza appena  calcolata (h) sommata al copriferro (H=h+delta).

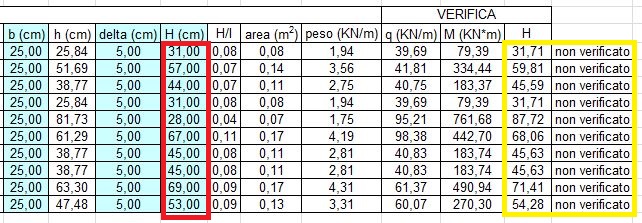
Come si può vedere l’altezza da noi inserita non è sufficiente quindi procederemo con l’aumentarla gradualmente finché non otterremo quella di verifica.

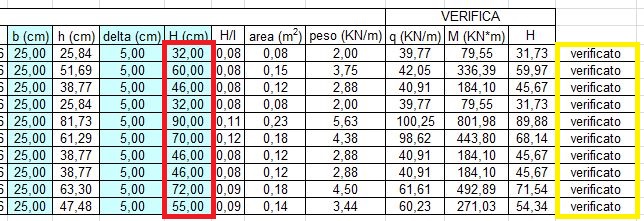
infine allego i file exel utilizzati per questa esercitazione.

TRAVE RETICOLARE SPAZIALE

MODELLAZIONE

Le travi reticolari spaziale sono utilizzate spesso per superare grandi luci. Per questa esercitazione ho preso in esame un ponte pedonale che deve coprire una distanza totale di circa 100 metri per una larghezza di 21 m. Utilizzeremo Travi reticolari con geometria a “triangoli” e per la modellazione utilizzeremo Autocad 3D ricordando che le linee del che costruiremo corrispondo al baricentro delle sezioni delle travi nel software SAP2000. Quest’ultimo strumento ci servirà per i calcoli di tipo meccanico e strutturale.

Iniziamo con l’avvio di Autocad

Nella visualizzazione Wareframe 2D e sul piano XY facciamo un punto con le coordinate 0,0 e cioè in origine. Il nostro disegno sarà costruito con riferimento a questo punto poiché il modello sarà più facilmente controllabile in SAP2000.

Ora disegneremo la curvatura del ponte.
Con una linea andiamo 50 metri a destra dal punto, ne facciamo un’altra della stessa lunghezza a sinistra e una terza che dall’origine va verso l’altro per una lunghezza di 10 metri

Con il comando arco andiamo a cliccaresugli estremi delle linee che abbiamo pocanzi disegnato.

Eliminiamo tutto tranne il punto in origine e la porzione di circonferenza. Una volta fatto ciò con il comando dividi sezioniamo l’arco in 13 parti. Tracciamo una linea che colleghi tutti i punti che abbiamo ottenuto con il comando dividi.

Ora eliminiamo l’arco e i punti. Quella che resta è una spezzata formata da linee spezzate.

Entriamo nella visualizzazione 3D e ruotiamo con “Ruota 3D” l’intera spezzata facendo perno sull’origine e selezionando il piano di rotazione YZ (anello rosso)

Copiamo la spezzata in direzione Y con una distanza di 7 metri e colleghiamo i vertici delle spezzate a formare prima quadrati poi con le diagonali triangoli

Quelle appena disegnate sono le basi delle “piramidi”. Cambiamo colore e utilizziamo il rosso. Per trovare i vertici dobbiamo ruotare l’UCS in modo da avere l’asse Z parallelo all’asse Y globale e con il comando arco  punti creiamo di nuovo l’arco generatore della spezzata nel mezzo delle nostre basi (nel punto medio delle diagonali). Questa volta però fremo un offset di 3,5 m verso il centro e divideremo l’arco così ottenuto in 12 parti. I medesimi devono essere collegati da una spezza che sarà l’insieme delle travi che collegano i vertici delle “piramidi”

Con il colore blu colleghiamo il vertice alle basi sempre con linee

Riportiamo l’UCS nella configurazione globale e specchiamo i segmenti finora disegnati per ottenere un’altra fila di “piramidi” adiacenti a quelle tracciate con le diagonali bianche incidenti anziché parallele. Per ora non ci preoccupiamo delle linee sovrapposte.

In magenta ho evidenziato l’asse del comando specchia.

Non resta che ripetere l’operazione per un’atra volta al fine di ottenere l’ultima campata di “piramidi e collegare le spezzate rosse prima disegnando quadrati e poi le diagonali.

Prima di esportare bisogna:

-          “ESPLODERE” tutti gli elementi che abbiamo disegnato

-          Utilizzare il comando _OVERKILL per eliminare tutte le sovrapposizioni

-          Creare un LAYER differente da 0 (zero) che chiameremo per esempio FRAME e spostarci tutti gli elementi

Come ultima accortezza esportare con la versione DXF più vecchia

IMPORTAZIONE MODELLO IN SAP2000

Una volta avviato SAP2000 andare su File>Importa>Autocad .dxf file per importare il dxf. Si aprirà una finestra in cui dobbiamo cambiare le unità di misura nel menù a tendina in kN, m, C che corrispondono a unità di misura di forza lunghezza e apertura angolare.

Clicchiamo su Ok e si aprirà una nuova finestra. Nel menù a tendina di Telai selezioniamo il layer FRAME e clicchiamo su Ok.

PREDISPOSIZIONE MODELLO

Nella vista 3D controlliamo se ci sono errori di modellazione eventualmente li correggiamo

Selezioniamo tutta la struttura e tramite Edita>Edita Punti>Unisci Nodi elimineremo le piccole imperfezioni che ad occhio non percepiamo.  La Tolleranza di 0,1 è sufficiente.

Ora rilasceremo i momenti ai vertici delle aste in modo da impostare le cerniere interne. Selezioniamo l’intero modello poi andiamo su Assegna>Frame>Rilasci/Rigidezze Parziali. Quindi spuntiamo le caselle di inizio per Torsione e di inizio e fine per Momento 2.2 (minore) e Momento 3.3 (maggiore).

Per vedere se abbiamo fatto tutto correttamente verifichiamo se tutte le aste terminano con un pallino verde.

Assegniamo i vincoli esterni, cerniere da una parte e carrelli dall’altra: per farlo bisogna selezionare i punti e andare su Assegna>Nodo>Vincoli Esterni…  e selezioniamo Traslazione 1, Traslazione 2 e Traslazione 3 per le cerniere e solo traslazione 3 per i carrelli.

ASSEGNAZIONE CARICHI

Ora dobbiamo caricare il ponte. Come abbiamo detto all’inizio di tratta di un ponte pedonale. Immaginiamo che il pavimento sia un assito in legno spesso 20 cm in media quindi come CARICO PERMANTE avremo:

PESO_SPECIFICO_LEGNO X SPESSORE = PESO A METRO QUADRO
6,5 kN/m³ x 0,20 m =1,3 kN/m²

Mentre la normativa prevede un CARICO ACCIDENTALE corrispondente a una folla con un carico diffuso di

3,92 kN/m²

Per questo esercizio non consideriamo il peso strutturale.

In totale il carico su m² è
CARICO PERMANTE + CARICO ACCIDENTALE = 1,3 kN/m² + 3,92 kN/m² = 4,22 kN/m²

I vertici al centro sostengono circa 49 m² di pavimento per un carico complessivo di 206,78 kN.

I vertici ai bordi sostengono circa 24,5 m² di pavimento per un carico complessivo di 103,39 kN.

Ora selezioniamo i vertici sul ponte cominciando da quelli sul bordo. Poi su Assegna>Carichi Nodo>Forze… andiamo a creare un nuovo caso di carico cliccando sul pulsante + che sta vicino alla scritta DEAD

Nella finestra che si apre andiamo a creare un nuovo caso di carico dal nome CARICHI CONCENTRATI e con un moltiplicatore di peso proprio uguale a zero.

Clicchiamo ok e nella finestra precedente andiamo a selezionare il nuovo caso di carico mentre inseriamo il valore -103,39 kN. Inseriamo il valore negativo poiché la forza è diretta verso il basso.

Nella vista 3D possiamo osservare le forze applicate.

Ora selezioniamo i nodi centrali e assegniamo un valore di -206,78 kN.

ASSEGNAZIONE SEZIONE

Selezioniamo l’intera struttura e assegniamo la sezione attraverso Assegna>Frame>Sezione Frame… clicchiamo su Aggiungi Proprietà Sezione Frame quindi su Tubo. In quest’ultima finestra cambiamo nome alla sezione (per esempio tubo20) e cambiamo la dimensione del raggio esterno in 0,2 m mentre lo spessore 0,01.

Una volta premuto su ok ci apparirà la finestra Proprietà Frame. Selezioniamo la sezione TUBO20 e quindi ok.

Come verifica sulla visualizzazione 3D comparirà vicino alle aste il nome sella sezione.

ESECUZIONE ANALISI

Lanciamo l’analisi con il pulsante F5. Nella finestre che si apre selezioniamo DEAD e MODAL e clicchiamo su Esegui/Non Eseguire Caso. Nella colonna Azione comparirà Do Not Run. Poi selezioniamo CARICHI CONCENTRATI e clicchiamo su Esegui Ora.

Appena finito il calcolo la visualizzazione 3D ci mostra la deformata che è sproporesagerata. Per verificare che non abbiamo fatte errori clicchiamo sul pulsante Mostra Sollecitazioni/Tensioni>Fame/Cavi/Tiranti. La finestra che si apre ci permette di selezionare le sollecitazioni che vogliamo visualizzare. Nel nostro caso Mom. 3-3 perché le travi reticolari se correttamente costruite hanno solo sforzi normali

Effettivamente non ci sono diagrammi quindi non ci sono momenti. Per maggior sicurezza possiamo cliccare con il tasto destro del mouse su una qualsiasi asta.

Ora visualizziamo i diagrammi delle Normali in modo da visualizzare velocemente quali travi sono più sollecitate. Per mostrarle andiamo su Mostra Sollecitazioni/Tensioni>Fame/Cavi/Tiranti. La finestra che si apre  selezioniamo la componente  F. Assiale. Quindi clicchiamo su OK

Nella visualizzazioen 3D possiamo vede queli sono le zone dove le aste sono più caricate in particaolare il colore blu solo le sollecitazioni a trazione e sono più evidenti della porzione bassa, mentre in rosso la sollecitazione a compressione che è più evidente nella parte superiore della struttura

Per valutare gli spostamenti e confrontarli con la cofigurazione iniziale andiamo su Mostra Geometria Deformata…  poi nella finestra mettiamo la spunta su cubica  e campitura.

 In blu troveremo la deformata mentre in grigio la configurazione iniziale. Inoltre se passiamo con il puntatore sui nodi verrano mostrati gli spostamenti U1 (x),U2 (y)eU3 (Z)

Ora però nasce l’esigenza di controllare numericamente le sollecitazione e gli spstamenti.

TABELLE SPOSTAMENTI E TABELLE SOLLECITAZIONI

Per produrre le tabelle andiamo su Visualizza>Mostra Tabelle… ci si aprirà una finestra . Innanzitutto andiamo a selezionare il solo schema di carico che ci interessa CARICO PUNTUALE cliccando su Sel. Schemi di carico. Deselezioniamo DEAD e diamo Ok. Sulla finestra Scegli Tabelle da Mostrare spuntiamo RISULTATI DELL’ANALISI quindi diamo Ok

Per adesso ci interessano solo due tabelle Joint Displacements per gli spostamenti e Element Stresses – Frames per la tensione interna.

Iniziamo con la tabella spostamenti. Per adesso valutiamo questi spostamenti solo a spanne anche perché non conosco i limiti normativi ne l’esperienza per dire se sono eccessivi oppure ragionevoli. Dal menù a tendina selezioniamo la tabella Joint Displacements .

Per gestirla agevolmente la esportiamo su Exels File>Esporta Tabella Corrente>Su Exels. Ordiniamo in modo crescente (vanno verso il basso quindi hanno valore negativo, il valore più basso quindi coincide con lo spostamento maggiore) gli sposamenti verticali U3 che in generale hanno valore più elevato rispetto gli spostamenti orizzontali U1 e U2

Lo spostamento maggiore è sul nodo 13 con valore -3,50461 il che vuol dire che si abbassa di ben 3,5 metri. Su una luce di cento metri può sembrare poco ma secondo me la deformazione a pieno carico è notevole probabilmente un modo per limitare gli spostamenti è quello di aumentare le sezioni lette travi. Abbiamo scelto travi tubolari di diametro 20 cm e spessore 1 cm quindi è sottodimensionato.

Ordiniamo anche U1 per vedere quanto “scorre” e lo spostamento maggiore è sui nodi vicino ai carrelli esterni. È uno spostamento di 85 cm quindi anche questo non può essere sottovalutato. In questo caso la soluzione può essere banalmente quella di applicare delle cerniere esterne al posto carrelli. Ma pensandoci bene se c'è meno scorrimento ci dovrebbe essere anche meno abbassamento. quindi irrigidire i vincoli potrebbe avere come risvolto anche il problema dell'abbassamento eccessivo.

Per le sollecitazioni dobbiamo esportare la tabella Element Stresses – Frames con lo stesso procedimento dellaJoint Displacements. Questa tabella non riporta la forza normale ma la tensione a cui sono sottoposte le travi. Ho scelto questa modalità perché avendo inserito una sezione in precedenza, posso verificare se questa sia sufficientemente resistente. La tipologia di acciaio che abbiamo inserito è identificata da una sigla, questa è A992Y50. A992 è la sigla che identifica un protocollo internazionale di classe di acciaio e Y50 sta per Y come yield o ancora meglio come tensione di crisi o snervamento e 50 sono i ksi ossia 1000 x psi (1 libbra/inch²). In SAP 2000 all’inizio però abbiamo deciso di utilizzare i kN come unità di misura della forza e i m come unità di misura dello spazio. Dobbiamo quindi fare le equivalenze tra 50 ksi e i kN/m².

1 ksi = 6894,75 kN/m²

50 ksi = 344737,86 kN/m²

Se la tensione massima che troviamo nella struttura è minore di 344737,86 kN/m² allora la struttura è verificata allo sforzo normale.

Quindi prendiamo la tabella Element Stresses – Frames  su Exels e ordiniamo le S11 prima in modo crescente per vedere la compressione massima poi in ordine decrescente per trovare la tensione massima

Come si può leggere per la tensione abbiamo un valore di 1346438,24 kN/m² che è 4 volte sopra alla resistenza di riferimento mentre arriviamo a 1049676,91 kN/m² di compressione che è 3 volte sopra la resistenza di riferimento.

In sostanza la struttura realizzata con quella sezione non è verificata quindi deve essere riprogettata soprattutto considerando il fatto che non abbiamo ponderato ancora il peso strutturale.

TRAVE RETICOLARE ISOSTATICA BIDIMENSIONALE

Questa esercitazione tratta delle strutture reticolari. In questa prima fase studierò una trave reticolare bidimensionale isostatica, dalle reazioni vincolari alle caratteristiche della sollecitazione attraverso il metodo delle sezioni di Ritter.
La trave che prendo in esame è costituita da tre campate di 6m di base per 3 m di altezza per la lunghezza totale di 18 m. Per semplificare i calcoli utilizziamo la lunghezza L di riferimento con L=3m. Come tutte le travi reticolari gli elementi che la compongono sono collegati tra essi tramite una cerniera interna. Ho applicato poi una cerniera esterna sul punto A mentre un carrello esterno sul punto H. I carichi concentrati vengono applicati sui nodi nei punti B, D e G. In questo caso ho messo tre carichi verticali pari a F diretti verso il basso.

REAZIONI VINCOLARI

La soluzione delle reazioni vincolari è piuttosto veloce se si considera che la trave ha una configurazione geometrica simmetrica ed è caricata simmetricamente. Dunque il carico totale 3F sarà diviso in parti uguali nelle reazioni vincolari pertanto avremo 3/2 L verso l'alto sia in A che in H.

CARATTERISTICHE DELLA SOLLACITAZIONE

Cominciamo con lo studio delle caratteristiche della sollecitazione attraverso il metodo delle sezioni di Ritter sapendo che consideriamo il peso strutturale trascurabile e quindi nullo e che nelle travi reticolari caricate sui nodi le sollecitazione delle aste sono tutte parallele alle direzioni delle aste a cui appartengono e cioè sono normali alla sezione trasversale quindi avremo solo elementi compressi o tesi. inoltre posso analizzare anche solo metà delle aste in quanto, come detto in precedenza, la struttura è simmetrica e simmetricamente caricata pertanto anche le sollecitazioni sono simmetriche.

La prima sezione la eseguiamo sulle aste 1 e 2.

Visto che le forze in giuoco sono solo tre allora possiamo pensare di risolvere facilmente il sistema con il metodo grafico. Infatti le tre rette d'azione creano un triangolo rettangolo in cui due lati formano un angolo di 45 gradi: è un triangolo isoscele e conosciamo un cateto, visto che è la reazione vincolare 3/2 F, sappiamo immediatamente quale è il valore dell'altro cateto. L'ipotenusa la troviamo facilmente in quanto è un cateto moltiplicato per la radice di due.

Possiamo osservare che l'asta 1 è compressa, quindi è un puntone, mentre la 2 è tesa, quindi è un tirante.

Ora faccio una sezione che intersechi le aste 2, 3 e 4.

Questa volta lo schema non è semplice come quello della sezione precedente, la strada più semplice per la soluzione è quella che prevede l'utilizzo di equazioni di equilibrio alla rotazione che annullino di volta in volta una incognita e magari qualche altra forza nota al fine di semplificare i calcoli. Iniziamo con l'equazione dell'equilibrio alla rotazione calcolata nel punto C per trovare la sollecitazione dell'asta 4

-3/2F·2L+F·L-N₄·L=0
N₄=-2L

Il segno negativo di N4 ci informa del fatto che abbiamo sbagliato il verso ipetetico della forza quindi la è entrante anziché uscente.

Per scoprire quale è il valore di N₃ facciamo la rotazione all'equilibrio nel punto A

-F·L+2F·L-N₃·√2L=0
N₃=√2/2·F

 

Rimane una ultima sezione e più precisamente quella che interseca le aste 4, 5, e 6.
 

Come con la sezione precedente per scoprire il valore di N₅ e N₆ utilizziamo le equazioni ni equilibrio alla rotazione.
Iniziamo con l'equazione di equilibrio alla rotazione sul punto D per trovare N₆.

-3/2·3L+F·2L+N₆·L=0
N₆=5/2·F

Ora con l'equazione di equilibrio alla rotazione sul punto A troviamo N₅.

-F·L+2F·L+N₅·√2L=0
N₅=-√2/2·F

Adesso sono note tutte le caratteristiche della sollecitazione e posso disegnare il diagramma nelle normali.

Come è possibile osservere le aste più sollecitate sono quelle ai bordi del sistema e più in specifico sono il puntone diagonale adiacente al vincolo (3/2·F) e il tirante centrale (√2/2·F).

La successiva fase è il controllo della trave reticolare attraverso il software SAP2000. Per rendere confrontabili i risultati devo però attribuire a F un valore in termini fisici. Immagino che la struttura reticolare sia adibita a copertura non praticabile e, ignorando i carichi strutturali della struttura e i sovraccarichi permanenti, applico solo i sovraccarichi accidentali che sono tabellati dalle NTC D.M. 14 gennaio 2008 cioè F=1,2 kN

 

Malgrado il tirante centrale sia il più sollecitato, non necessariamente sarà il tratto con una sezione dimensionalmente più grande. La trave 4 e la corrispondente simmetrica ( ma in generale tutte le travi compresse) devono infatti dare conto del carico di punta ovveroquel caso in cui la sezione resistente rispetto alla lunghezza della trave risulti snella. Nel tal caso anche a parità di superficie resistente, la trave dovrà avere un ingombro maggiore.

A breve la seconda parte che tratterà della trave reticolare bidimensianle sul software SAP2000.

Salve a tutti sto provando a caricare una immagine random tanto per predere confidenza con il blog.