ESERCITAZIONE 3

Devo risolvere il sistema formato da una trave iperstatica con l’equazione della linea elastica.

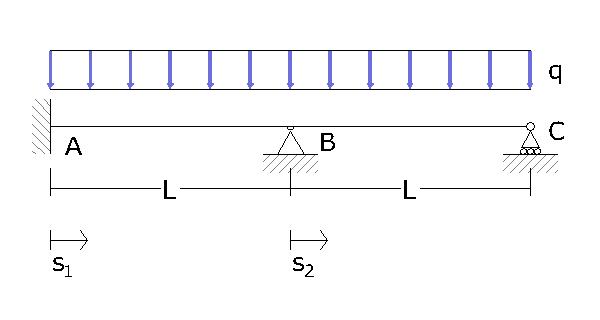
Prima di fare i calcoli faccio un’analisi qualitativa. Questa mi aiuterà a capire e a controllare i risultati. Incomincio disegnando una ipotetica deformata.

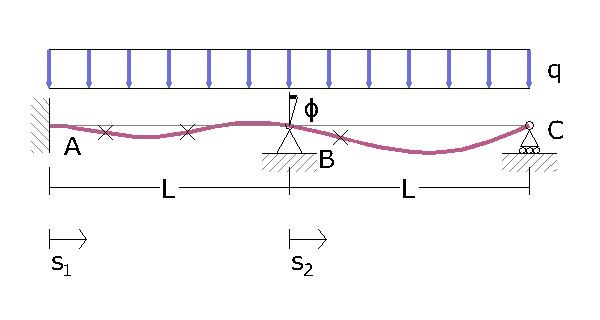
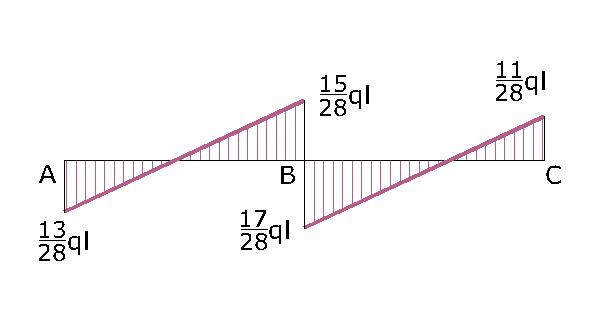
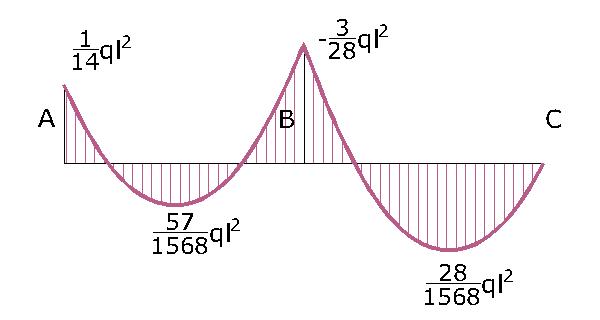
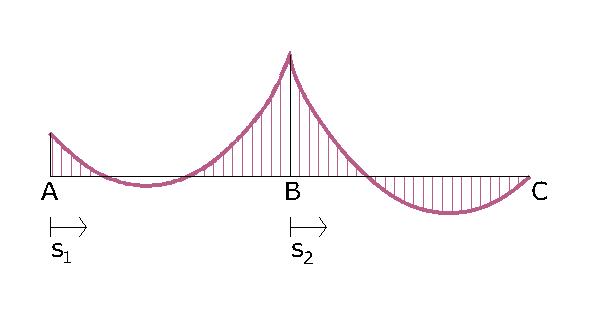
Il sistema ha una spiccata asimmetria. La trave si deforma maggiormente dove è meno rigida, in questo caso in quella parte dove è meno vincolata. Inoltre so che in corrispondenza del vincolo cerniera in B mi aspetto una singolarità. I primi due punti di flesso sono sicuramente all’interno del segmento AB mentre il terzo nel segmento BC, anche se per adesso non so quali siano i punti precisi. I punti di flesso sono quei punti dove la curvatura è nulla e in quei punti certamente anche  il momento è nullo. Per disegnale qualitativamente il diagramma dei momenti quindi mi è rimasto da definire il tipo di funzione ma è facile se osservo il carico costantemente distribuito q2, infatti se q2 è –q il taglio sarà lineare mentre il momento parabolico. In A c’è un incastro e mi aspetto un valore diverso da zero mentre in B in corrispondenza della singolarità mi aspetto una cuspide, infine in C il momento è nullo perché ci troviamo su un vincolo carrello.

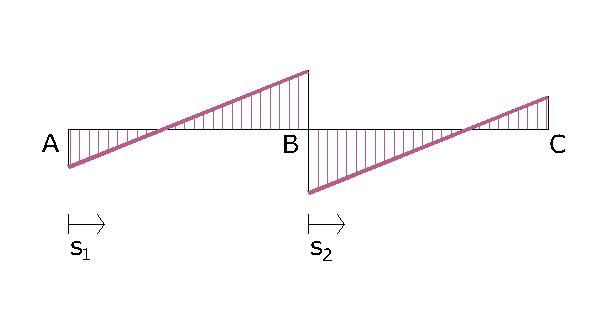
A questo punto analizzo il taglio. Come già detto in precedenza il taglio è lineare a ha la stessa inclinazione per tutti i tratti:

- nel tratto BC il punto di nullo è più vicino a C perché il vertice della parabola si trova nello stesso punto

- nel tratto AB il punto di nullo, corrisponde al vertice della parabola del momento ed è evidentemente vicino ad A

So che in B c’è una singolarità quindi devo analizzare la trave con due equazioni differenti. Per non confondermi, utilizzo una nomenclatura univoca per indicare gli elementi nel modo più preciso possibile. Quindi utilizzo il pedice 1 e le costanti di integrazione C per tutti gli elementi che si trovano nel tratto AB e il pedice 2 e le constanti di integrazioni D per tutti gli elementi che si trovano sul tratto BC.

L’equazione della linea elastica per il tratto 1 è:

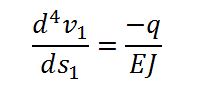
Di conseguenza l’equazione dello spostamento è:

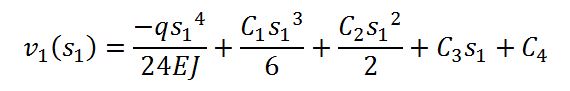
L’equazione della linea elastica per il tratto 1 è:

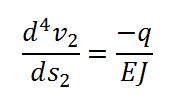
Di conseguenza l’equazione dello spostamento è

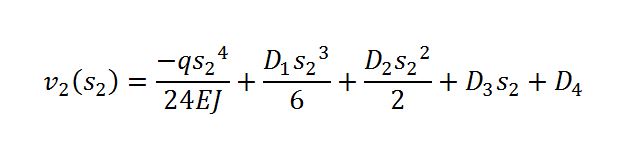
Ora definisco le condizioni al contorno si cinematiche che statiche

A             nell’incastro vengono impedite le traslazioni assolute e le rotazioni assolute

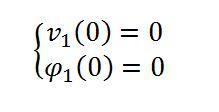
B             per questo punto devo fare un ragionamento più complesso perché devo capire la relazione tra le due parti della trave e il significato meccanico della continuità. Il vincolo cerniera ci dice che gli spostamenti non sono consentiti ma sono consentite le rotazioni. Ma se è vero che il vincolo non blocca le rotazioni assolute, nulla midice sulle rotazioni relative. Queste infatti sono nulle perché la trave è continua e dall’analisi qualitativa del momento ho visto anche che c’è continuità per questa sollecitazione.

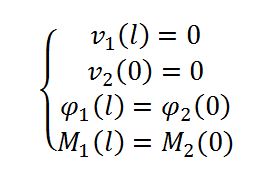
C             In questo punto trovo un vincolo carrello, pertanto ho sia una condizione al contorno cinematica sia una condizione al contorno statica:

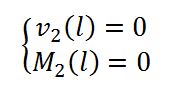
Prima di scrivere il sistema di otto equazioni e otto incognite che mi permetterà di trovare le costanti di integrazione della linea elastica, provo a determinare e semplificare velocemente costanti ed equazioni

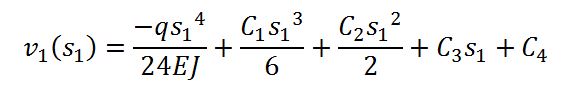
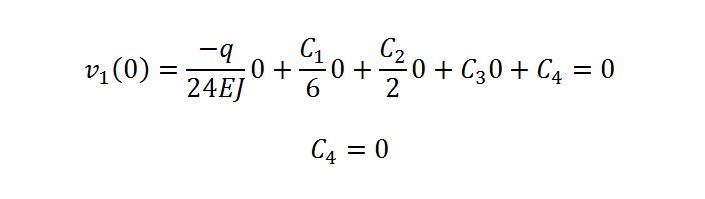
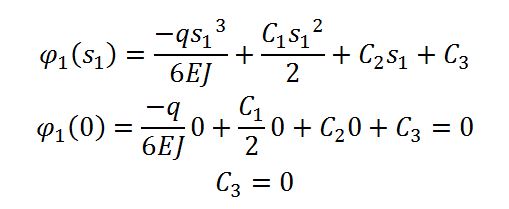
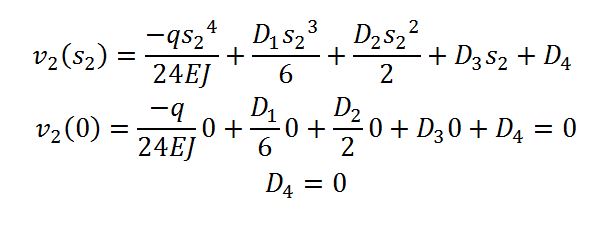
Ricapitolando

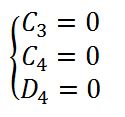
Quindi posso ridurre il problema in un sistema di cinque equazioni di cinque incognite

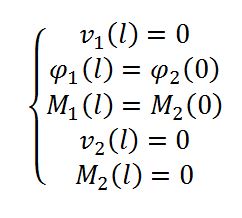
Adesso procedo con la risoluzione delle equazioni

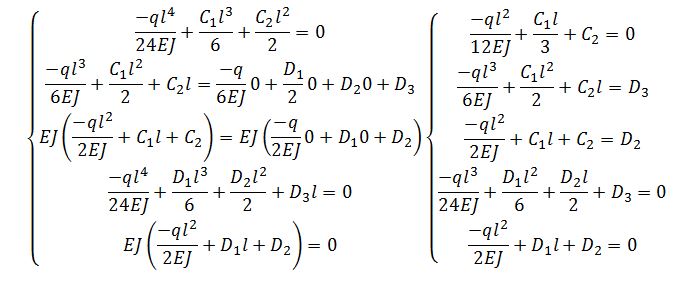
Ora prendo in esame le ultime due per trovare D3 in funzione di D2

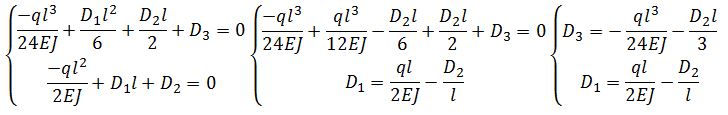
Adesso prendo in esame le prime tre

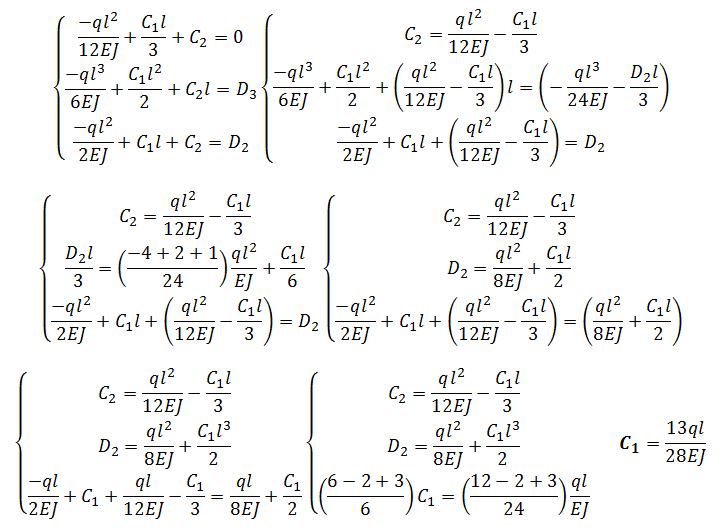
Attraverso più facili sostituzioni trovo che:

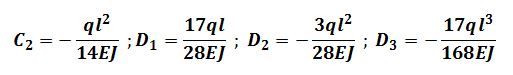
Quindi riscrivo le equazioni sostituendo le costanti di integrazione

Tramite queste equazioni riuscirò a capire come funziona per intero la struttura. Comincio con Taglio e Momento del tratto 1

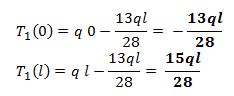
E vedo dove si annulla per sapere dove si trova il vertice della parabola del Momento:

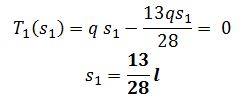
Come ipotizzato all’inizio, il vertice della parabola si trova più vicino ad A. Per il Momento otterrò:

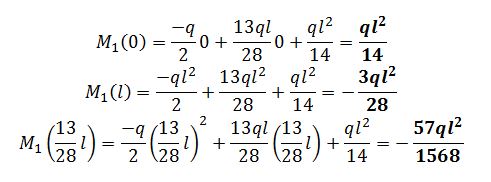
Ripeto i calcoli fatti per il tratto 1 sul tratto 2

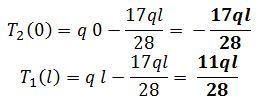
E vedo dove si annulla per sapere dove si trova il vertice della parabola:

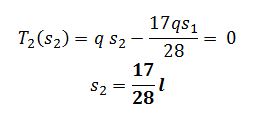
Di nuovo viene confermata l’ipotesi iniziale della posizione del vertice della parabola cioè più vicina al punto C. Ora calcolo il Momento sapendo però che è dato dalle condizioni al contorno:

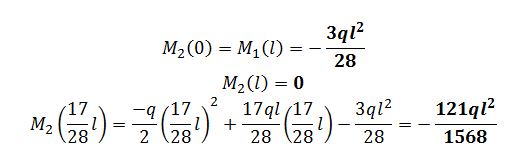
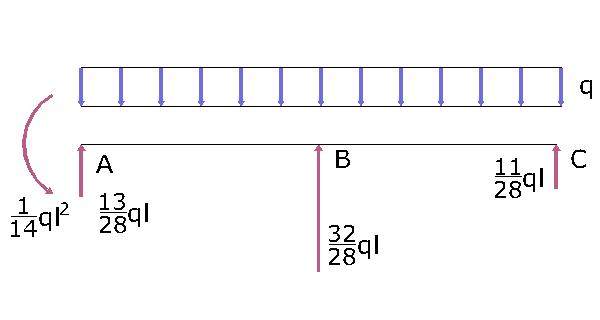
Disegno i diagrammi delle sollecitazioni dai quali evincerò le reazioni vincolari.