Esercitazione 2_ Dimensionamento di una trave di legno, cemento armato e acciaio.

Esercitazione2_ Dimensionamento di una trave

1_ Analisi edificio

L’edificio analizzato è una semplice abitazione (uso residenziale), con una parte su due livelli, dotato di schema strutturale molto semplice.

Questo è caratterizzato da un’orditura di travi principali dotate di una luce di 6m, e di travi secondarie (e perimetrali) lunghe 4m.

La prima cosa da fare, partendo dallo schema della carpenteria è capire quale è la trave più sollecitata, sapendo che ogni trave principale si prende metà del peso del solaio che regge.

In questo caso è stata individuata la trave B-B’ come una delle più sollecitate, in quanto si carica del peso del solaio che ha sia a destra che a sinistra, avendo perciò un interasse totale di (2+2=) 4 m.

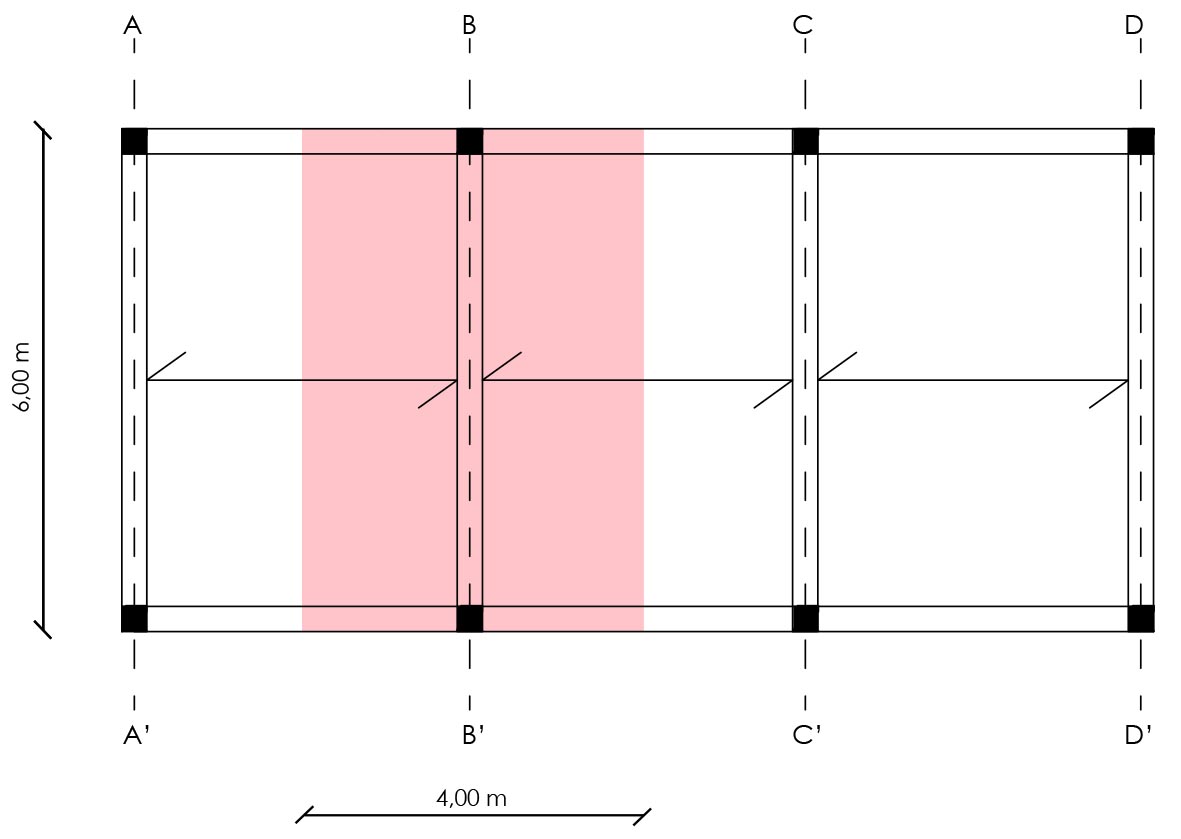
2_ Scelta del tipo di solaio

Si è scelto di fare un’analisi di questa trave, studiandola in relazione ai diversi materiali da costruzione: si sono perciò analizzate diverse stratigrafie di solaio in base alla trave che di volta in volta si vuole analizzare.

2.1_ Solaio in legno

                                

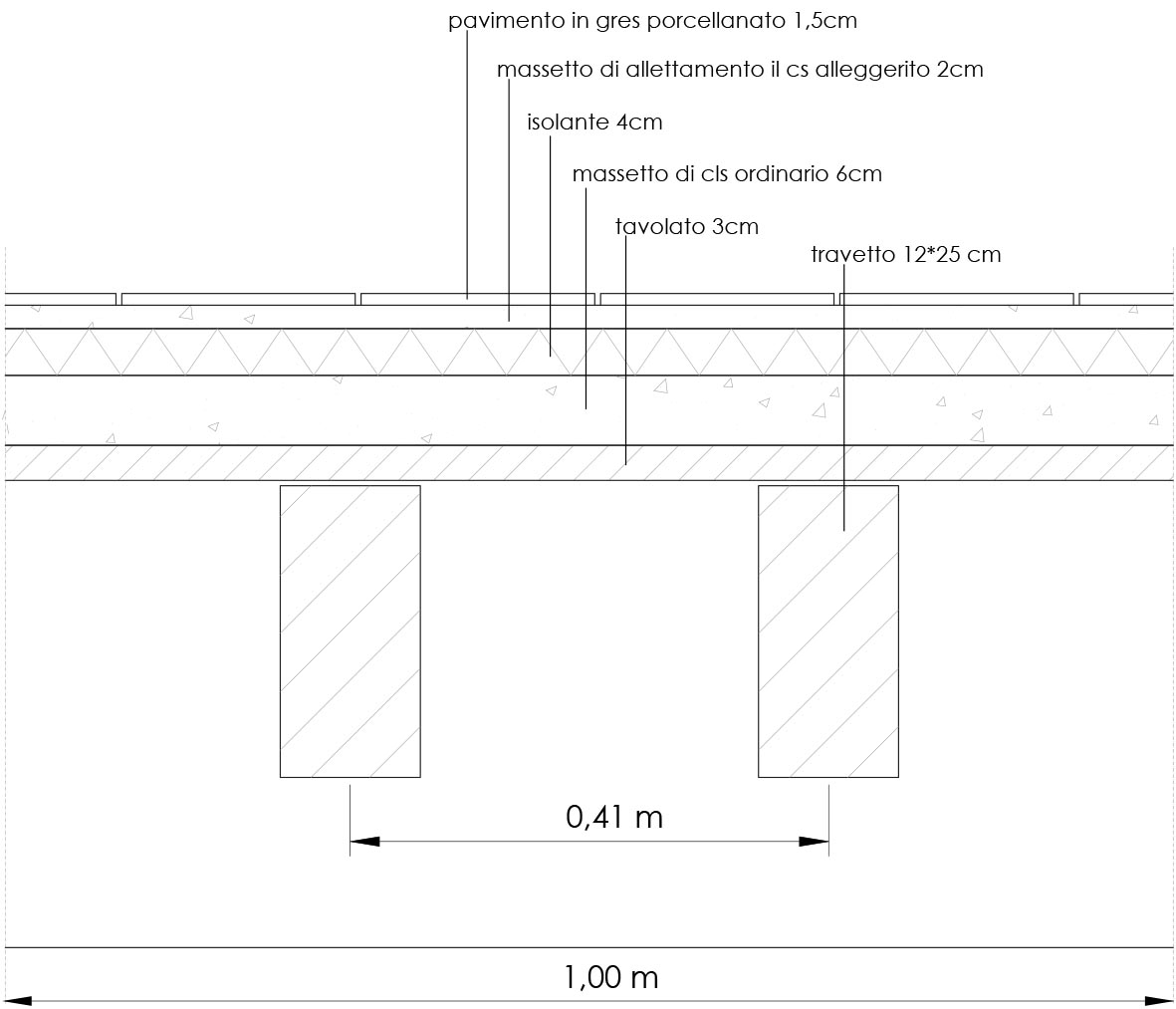
Il primo passo per l’analisi dimensionale della trave, è lo studio dei carichi che questa deve sopportare. Questi si dividono in carichi strutturali q_s, carichi permanenti q_p, carichi accidentali q_A.

È necessaria l’analisi di questi tre tipi di carichi separatamente, e poi devono essere uniti per ottenere il carico complessivo del solaio.

Analisi carichi solaio in legno

_carichi strutturali q_s : tavolato, travetti

_tavolato 0,03 m * 4kN/m³ = 0,12 kN/m²

_travetti   2 * 0,25 m* 0,12 m * 6 kN/m³ = 0,36 kN/m² (viene usato il valore al mq perché non c’è grande differenza con quello che si avrebbe al ml)

_totale q_{s =} 0,48 kN/m²

 

_carichi permanenti q_p : pavimento, allettamento, isolante, massetto, incidenza impianti e tramezzi

_pavimento in gres porcellanato 0,015 m * 20 kN/m³ = 0,3 kN/m²

_massetto in cls leggero 0,02 m * 14 kN/m³ = 0,28 kN/m²

_isolante 0,04 m * 0,4 kN/m³ = 0,016 kN/m²

_massetto cls  0,06 m * 24 kN/m³ = 1,44 kN/m²

_incidenza impianti 1 kN/m²

_incidenza tramezzi 0,5 kN/m²

_totale q_p = 3,54 kN/m²

 

_carichi accidentali q_A:

_ambiente residenziale 2,00 kN/m²

_totale q_A: 2,00 kN/m²

 

_totale carichi 6,02 kN/m²

_coefficienti di sicurezza

Per aumentare la sicurezza del dimensionamento ogni carico va moltiplicato per un coefficiente di sicurezza (poco più grande di 1) e questi sono: γ_s = 1,3  γ_p = 1,3  γ_A= 1,5

_totale carichi (con coeff.sicurezza) = 8,23 kN/m²

_carico proprio della trave q_s

In questa prima fase del dimensionamento non è stato considerato il peso proprio della trave, che incide nei carichi strutturali, in quanto non si conoscono le dimensioni della sezione. Tuttavia, una volta ricavata la sezione con il predimensionamento, verrà moltiplicata per il peso specifico del materiale con cui è composta. Verrà poi effettuato un nuovo dimensionamento, aggiungendo il valore del peso della trave ai carichi strutturali, ottenendo così un nuovo momento flettente, e valutando così la resistenza della trave.

 

3.1_ Dimensionamento

Dal valore di carico calcolato su un mq di solaio, si è risaliti alla quantità di carico del pezzo di solaio che grava sulla trave scelta. (kN/m)

 

q = (q_s * γ_s + q_p  *γ_p+ q_A *γ_A) * i = 8,23 kN/m² * 4 m =

q =32,92 kN/m

Successivamente al calcolo del carico distribuito che insiste sulla trave, è possibile calcolare il momento massimo M_max che insiste sulla sezione della stessa. In questo caso, la trave trattata è una semplice trave appoggiata dotata di un momento massimo pari a M_max = ql²/8:

M_max = (32,92 kN/m * 6² m²  )/8 =

M_max =148,14 kN * m

Definito il momento massimo di progetto, è necessario stabilire il materiale con cui si vuole realizzare la trave, dal quale dipenderà la resistenza f_d. Nel caso del legno, la resistenza dipende dalla formula f_d = ( k_mod * f_k ) / γ_m dove f_k è la resistenza del materiale scelto(in questo caso legno lamellare classe GL 24 h), k_mod è un coefficiente che tiene conto dell’effetto sia della durata del carico che dell’umidità sulla resistenza. Infine γ_m è il coefficiente di sicurezza del materiale (in questo caso 1,45).

f_d = ( 0,8 * 24 N/mm² ) /1,45 =

f_d = 13,24 N/mm²

Una volta ricavata la resistenza di progetto del materiale è possibile effettuare il dimensionamento attraverso la formula di Navier :  σ_amm= M_max/ W_max

Sapendo che W_max = bh²/ 6, stabilendo un valore per la base della trave (=30 cm) è possibile ricavare, tramite la formula inversa l’altezza: h= √ (6 * M_max) / (σ_amm * b)

 

h= √ (6 * 148,14 kNm) /[ (13,24 * 1000 kN/m² ) * 0,3 m]

h= √ 888,84 kNm / 3972 kN /m

h= √0,2237 = 0,473 m

L’altezza minima per la trave è di 47,3 cm. Tuttavia visto che è un predimensionamento di minima, si sceglie di utilizzare una sezione di h= 50 cm.

4.1_ Verifica del dimensionamento

Per verificare il dimensionamento appena calcolato è necessario andare a ricalcolare i carichi, aggiungendo il peso proprio della trave, calcolato in base alla sezione. Il peso specifico del legno lamellare classe GL 24 h è di 3,80 kN/ m^3.

Analisi carichi solaio in legno

_carichi strutturali q_s : tavolato, travetti, trave

_tavolato 0,03 m * 4kN/m³ = 0,12 kN/m²

_travetti   2 * 0,25 m* 0,12 m * 6 kN/m³ = 0,36 kN/m² (viene usato il valore al mq perché non c’è grande differenza con quello che si avrebbe al ml)

_trave 0,5 m * 0,3 m * 3,80 kN/m³ = 0,57 kN/ m²  (“ “ “ )

_totale q_{s =} 1,05 kN/m²

_carichi permanenti q_p : pavimento, allettamento, isolante, massetto, incidenza impianti e tramezzi

_pavimento in gres porcellanato 0,015 m * 20 kN/m³ = 0,3 kN/m²

_massetto in cls leggero 0,02 m * 14 kN/m³ = 0,28 kN/m²

_isolante 0,04 m * 0,4 kN/m³ = 0,016 kN/m²

_massetto cls  0,06 m * 24 kN/m³ = 1,44 kN/m²

_incidenza impianti 1 kN/m²

_incidenza tramezzi 0,5 kN/m²

_totale q_p = 3,54 kN/m²

 

_carichi accidentali q_A:

_ambiente residenziale 2,00 kN/m²

_totale q_A: 2,00 kN/m²

 

_totale carichi (con coeff.sicurezza) = 8,97 kN/m²

 

_calcolo carico distribuito:

q = (q_s * γ_s + q_p  *γ_p+ q_A *γ_A) * i = 8,97 kN/m² * 4 m =

q =35,87 kN/m

_calcolo momento massimo:

M_max = (35,87 kN/m * 6² m²  )/8 =

M_max =161,4 kN * m

_calcolo h trave (in quanto il parametro della resistenza non ha subito variazioni):

h= √ (6 * 161,4 kNm) /[ (13,24 * 1000 kN/m² ) * 0,3 m]

h= √ 968,4 / 3972 kN /m

h= √0,244= 0,493 m

5.1_ Dati di progetto nella tabella Excel

Nella tabella Excel compaiono nelle varie caselle i vari addendi e fattori che devono essere sommati e moltiplicati fra loro al fine di ottenere il dimensionamento: nella prima riga c’è il dimensionamento della trave senza considerarne il peso proprio, nella seconda invece c’è il dimensionamento che tiene conto anche al peso proprio della trave.

6.1_ Conclusioni

Dai due diversi dimensionamenti si è potuto constatare come aggiungendo il peso proprio della trave, si ha avuto un incremento dell’altezza della trave di oltre 2cm.

Tuttavia, rimanendo larghi nell’arrotondamento dell’altezza del primo dimensionamento, la trave scelta è risultata idonea in entrambi i casi.

 

2.2_ Solaio in laterocemento

                    

 

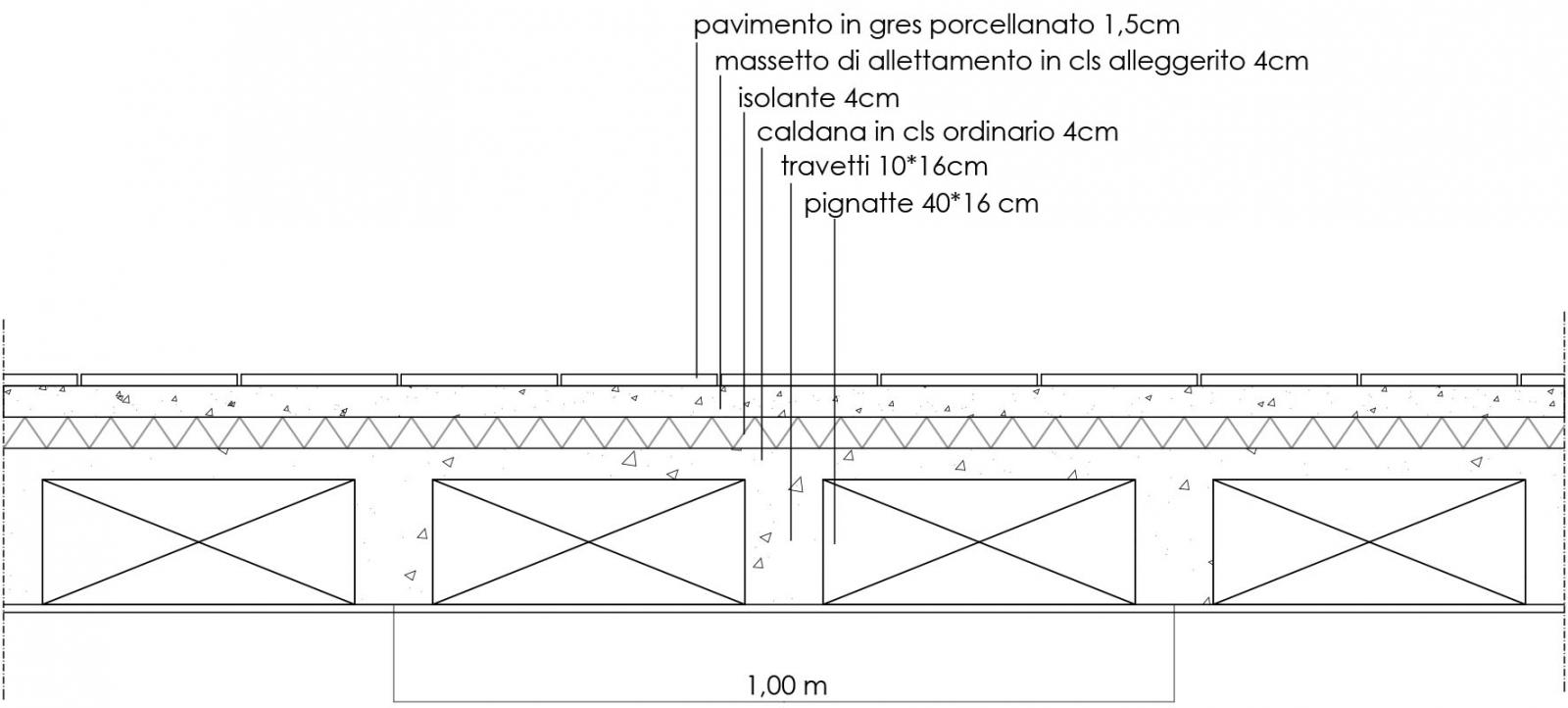
Analisi carichi solaio in laterocemento

_carichi strutturali q_s : caldana, travetti

_caldana 0,04 m * 24kN/m³ = 0,96 kN/m²

_travetti   2 * 0,10 m* 0,16 m * 24 kN/m³ = 0,77 kN/m² (viene usato il valore al mq perché non c’è grande differenza con quello che si avrebbe al ml)

_totale q_{s =} 1,73 kN/m²

_carichi permanenti q_p : pavimento, allettamento, isolante, pignatte, incidenza impianti e tramezzi

_pavimento in gres porcellanato 0,015 m * 20 kN/m³ = 0,3 kN/m²

_massetto in cls leggero 0,02 m * 14 kN/m³ = 0,28 kN/m²

_isolante 0,04 m * 0,4 kN/m³ = 0,016 kN/m²

_pignatte 2 * 0,4 m * 0,16 m * 8 kN/m³ = 1,02 kN/m²

_incidenza impianti 1 kN/m²

_incidenza tramezzi 0,5 kN/m²

_totale q_p = 3,12 kN/m²

 

_carichi accidentali q_A:

_ambiente residenziale 2,00 kN/m²

_totale q_A: 2,00 kN/m²

_totale carichi 6,85 kN/m²

_coefficienti di sicurezza

Per aumentare la sicurezza del dimensionamento ogni carico va moltiplicato per un coefficiente di sicurezza (poco più grande di 1) e questi sono: γ_s = 1,3  γ_p = 1,3  γ_A= 1,5

_totale carichi (con coeff.sicurezza) = 9,30 kN/m²

_carico proprio della trave q_s

In questa prima fase del dimensionamento non è stato considerato il peso proprio della trave, che incide nei carichi strutturali, in quanto non si conoscono le dimensioni della sezione. Tuttavia, una volta ricavata la sezione con il predimensionamento, verrà moltiplicata per il peso specifico del materiale con cui è composta. Verrà poi effettuato un nuovo dimensionamento, aggiungendo il valore del peso della trave ai carichi strutturali, ottenendo così un nuovo momento flettente, e valutando così la resistenza della trave.

3.2_ Dimensionamento

Dal valore di carico calcolato su un mq di solaio, si è risaliti alla quantità di carico del pezzo di solaio che grava sulla trave scelta. (kN/m)

q = (q_s * γ_s + q_p  *γ_p+ q_A *γ_A) * i = 9,30 kN/m² * 4 m =

q =37,2 kN/m

Successivamente al calcolo del carico distribuito che insiste sulla trave, è possibile calcolare il momento massimo M_max che insiste sulla sezione della stessa. In questo caso, la trave trattata è una semplice trave appoggiata dotata di un momento massimo pari a M_max = ql²/8:

M_max = (37,2 kN/m * 6² m²  )/8 =

M_max =167,4 kN * m

Definito il momento massimo di progetto, è necessario calcolare le resistenze dei due materiali che compongono la trave: l’acciaio f_yd (che ha una resistenza specifica per le armature) ed è data dal rapporto f_yd =f_yk/ γ_s e il calcestruzzo f_cd =α_cc * f_ck/ γ_c

f_yd = 450 N/mm² / 1,15

f_yd = 391,3 N/mm²

f_cd =0,85 * 40 N/mm² / 1,5

f_cd = 22,67 N/mm²

Una volta ricavata la resistenza di progetto del materiale è possibile effettuare il dimensionamento attraverso l’equilibrio alla rotazione della sezione:

M= C * b* = T * b*                          

Dove b*=hu-Xc/3                 Xc= α*hu                 α= σ_ca/ (σ_ca + σ_fa/n)    n=15

M= C * (hu- α*hu /3)

M= σ_ca * (b * α*hu)/2 * (hu- α*hu /3)

M= σ_ca * b * α*hu/2 * (1 – α/3)hu

2M= σ_ca * b * α * (1 – α/3)hu²

hu²= 2M / [σ_ca * b * α * (1 – α/3)]

hu= √2M / [σ_ca * b * α* (1 – α/3)]

Per calcolare l’altezza utile della sezione è necessario stabilire una base, in questo caso di 30 cm.

hu=√2 * 167,4 kNm / 10³ * 22,67 kN/m² * 0,3 m* 0,46 (1-0,46/3)

hu= 0,355 m = 35,5 cm

L’altezza minima per la trave è di 35,5 cm. Tuttavia nelle travi di cemento armato è necessario aggiungere un delta di 5 cm, che corrisponde all’altezza del copriferro e di metà della sezione dei tondini dell’armatura.

L’altezza che si ottiene dal predimensionamento quindi risulta essere H= hu+δ  H= 35,5 + 5 cm = 40,5 cm. Tuttavia si sceglie di rimanere larghi e prevedere una sezione di H=45 cm.

4.2_ Verifica del dimensionamento

Per verificare il dimensionamento appena calcolato è necessario andare a ricalcolare i carichi, aggiungendo il peso proprio della trave, calcolato in base alla sezione. Il peso specifico calcestruzzo armato è di 25 kN/m³.

Analisi carichi solaio in laterocemento

_carichi strutturali q_s : caldana, travetti

_caldana 0,04 m * 24kN/m³ = 0,96 kN/m²

_travetti   2 * 0,10 m* 0,16 m * 24 kN/m³ = 0,77 kN/m² (viene usato il valore al mq perché non c’è grande differenza con quello che si avrebbe al ml)

_trave 0,3 m * 0,45 m * 25 kN/ m³= 3,75 kN/m² (viene usato il valore al mq perché non c’è grande differenza con quello che si avrebbe al ml)

_totale q_{s =} 5,48 kN/m²

_carichi permanenti q_p : pavimento, allettamento, isolante, pignatte, incidenza impianti e tramezzi

_pavimento in gres porcellanato 0,015 m * 20 kN/m³ = 0,3 kN/m²

_massetto in cls leggero 0,02 m * 14 kN/m³ = 0,28 kN/m²

_isolante 0,04 m * 0,4 kN/m³ = 0,016 kN/m²

_pignatte 2 * 0,4 m * 0,16 m * 8 kN/m³ = 1,02 kN/m²

_incidenza impianti 1 kN/m²

_incidenza tramezzi 0,5 kN/m²

_totale q_p = 3,12 kN/m²

_carichi accidentali q_A:

_ambiente residenziale 2,00 kN/m²

_totale q_A: 2,00 kN/m²

_totale carichi 10,6 kN/m²

 

_coefficienti di sicurezza

Per aumentare la sicurezza del dimensionamento ogni carico va moltiplicato per un coefficiente di sicurezza (poco più grande di 1) e questi sono: γ_s = 1,3  γ_p = 1,3  γ_A= 1,5

_totale carichi (con coeff.sicurezza) = 14,17 kN/m²

_calcolo carico distribuito:

q = (q_s * γ_s + q_p  *γ_p+ q_A *γ_A) * i = 14,17 kN/m² * 4 m =

q =56,68 kN/m

_calcolo momento massimo:

M_max = (56,68 kN/m * 6² m²  )/8 =

M_max =255,1 kN * m

_calcolo hu trave (in quanto il parametro della resistenza non ha subito variazioni):

hu=√2 * 255,1 kNm / 10³ * 22,67 kN/m² * 0,3 m* 0,46 (1-0,46/3)

hu= 0,438 m = 43,8 cm

_aggiungo il coefficient δ per ottenere l’altezza H

H= 43,8 + 5 cm = 48,8 cm

Serve perciò una trave di altezza di 50 cm.

5.2_ Dati di progetto nella tabella Excel

Nella tabella Excel compaiono nelle varie caselle i vari addendi e fattori che devono essere sommati e moltiplicati fra loro al fine di ottenere il dimensionamento: nella prima riga c’è il dimensionamento della trave senza considerarne il peso proprio, nella seconda invece c’è il dimensionamento che tiene conto anche al peso proprio della trave.

6.2_ Conclusioni

Dai due diversi dimensionamenti si è potuto constatare come aggiungendo il peso proprio della trave, si ha avuto un incremento dell’altezza della trave molto incisivo: si passa da un’altezza utile di 35,5 cm ad un valore di 43,8, di oltre 8 cm superiore.

Questo è dovuto dal valore elevato del peso specifico del calcestruzzo armato, che influenza il dimensionamento quando si considera anche la trave con il suo peso.

2.3_ Solaio in acciaio

 

                          

 

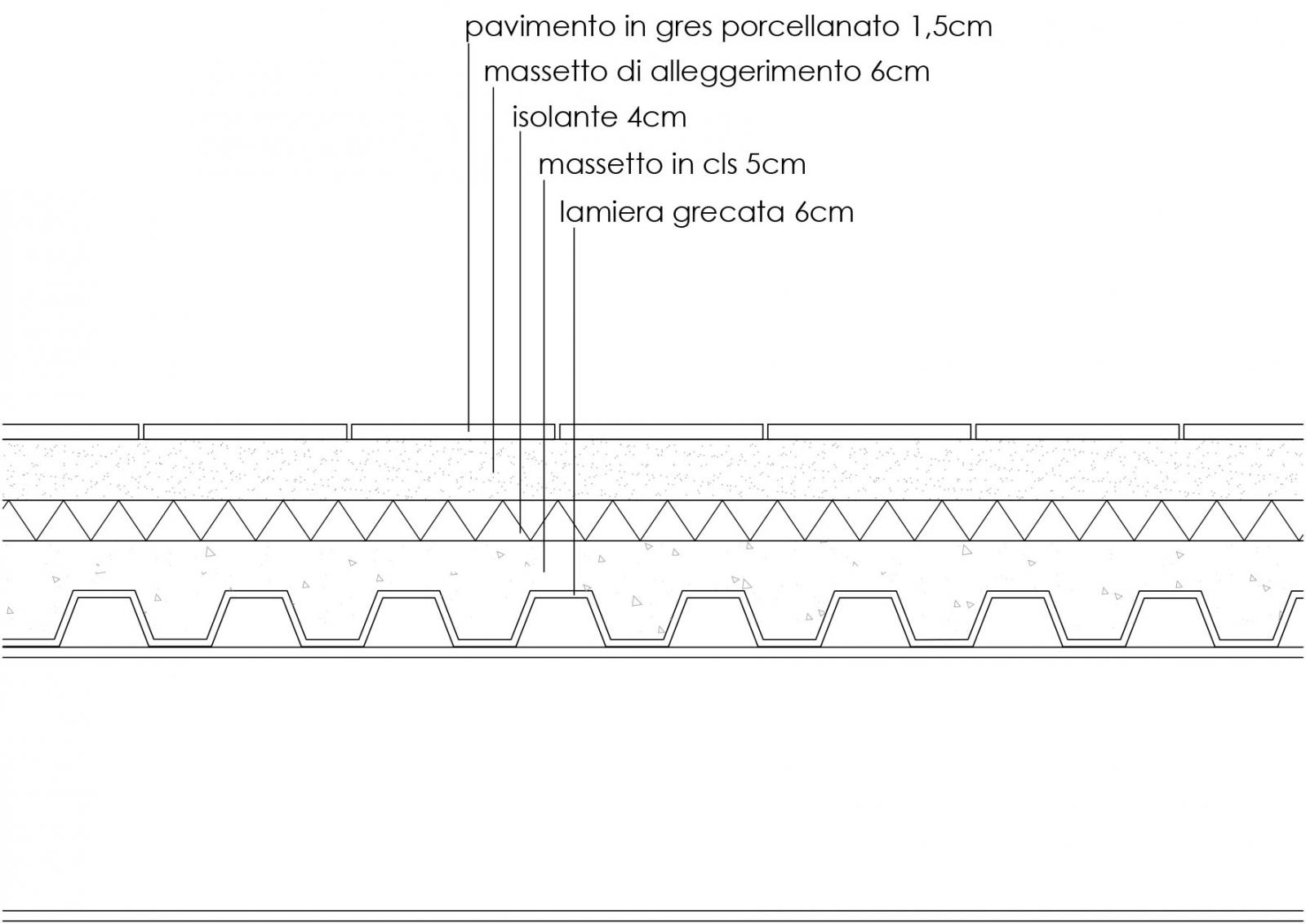
Analisi carichi solaio in acciaio

_carichi strutturali q_s : massetto in cls, lamiera grecata

_massetto in cls spessore 0,11 m= 2,15 kN/m²

_lamiera grecata tipo HI-BOND spessore 0,7mm = 0,09 kN/m²

_totale q_{s =} 2,24 kN/m²

_carichi permanenti q_p : pavimento, allettamento, isolante, incidenza impianti e tramezzi

_pavimento in gres porcellanato 0,015 m * 20 kN/m³ = 0,3 kN/m²

_massetto in cls leggero 0,06 m * 14 kN/m³ = 0,84 kN/m²

_isolante 0,04 m * 0,4 kN/m³ = 0,016 kN/m²

_incidenza impianti 1 kN/m²

_incidenza tramezzi 0,5 kN/m²

_totale q_p = 2,66 kN/m²

 

_carichi accidentali q_A:

_ambiente residenziale 2,00 kN/m²

_totale q_A: 2,00 kN/m²

_totale carichi 6,9 kN/m²

 

_coefficienti di sicurezza

Per aumentare la sicurezza del dimensionamento ogni carico va moltiplicato per un coefficiente di sicurezza (poco più grande di 1) e questi sono: γ_s = 1,3  γ_p = 1,3  γ_A= 1,5

_totale carichi (con coeff.sicurezza) = 9,37 kN/m²

_carico proprio della trave q_s

In questa prima fase del dimensionamento non è stato considerato il peso proprio della trave, che incide nei carichi strutturali, in quanto non si conoscono le dimensioni della sezione. Tuttavia, una volta ricavata la sezione con il predimensionamento, verrà moltiplicata per il peso specifico del materiale con cui è composta. Verrà poi effettuato un nuovo dimensionamento, aggiungendo il valore del peso della trave ai carichi strutturali, ottenendo così un nuovo momento flettente, e valutando così la resistenza della trave.

 

3.3_ Dimensionamento

Dal valore di carico calcolato su un mq di solaio, si è risaliti alla quantità di carico del pezzo di solaio che grava sulla trave scelta. (kN/m)

q = (q_s * γ_s + q_p  *γ_p+ q_A *γ_A) * i = 9,37 kN/m² * 4 m =

q =37,48 kN/m

Successivamente al calcolo del carico distribuito che insiste sulla trave, è possibile calcolare il momento massimo M_max che insiste sulla sezione della stessa. In questo caso, la trave trattata è una semplice trave appoggiata dotata di un momento massimo pari a M_max = ql²/8:

M_max = (37,48 kN/m * 6² m²  )/8 =

M_max =168,66 kN * m

Definito il momento massimo di progetto, è necessario stabilire il materiale con cui si vuole realizzare la trave, dal quale dipenderà la resistenza f_yd. Nel caso dell’acciaio, la resistenza dipende dalla formula f_yd = f_yk / γ_s dove f_yk è la tensione di snervamento del materiale scelto (in questo caso Fe 430/S275), e γ_s è il coefficiente di sicurezza relativo dell’acciaio (1,15).

f_yd = 275 N/mm²  /1,15 =

f_yd = 239,13 N/mm²

Una volta ricavata la resistenza di progetto del materiale è possibile effettuare il dimensionamento attraverso la formula di Navier :  σ_amm= M_max/ W_max

Avendo sia la tensione ammissibile che il momento massimo, posso utilizzare la formula inversa rcavandomi il modulo di resistenza minimo a flessione W_xmin

W_xmin= M_max /σ_amm

W_xmin= 168,66 kNm/10³ * 239,13 kN/m²

W_xmin= 0,0007053 m³= 705 cm³

Attraverso il prontuario delle IPE è possibile trovare l’altezza della trave corrispondente al modulo di resistenza a flessione. Il valore appena superiore al W_xmin calcolato è di 713,0 cm³, che corrisponde ad un IPE330.

L’altezza della trave calcolata con il predimensionamento è di 33 cm.

4.3_ Verifica del dimensionamento

Per verificare il dimensionamento appena calcolato è necessario andare a ricalcolare i carichi, aggiungendo il peso proprio della trave, calcolato in base alla sezione. Il peso specifico dell'acciaio è di 78,5 kN/m³ e l’area dell’IPE330 è pari a 62,60 cm² (=0,00626 m²)

Analisi carichi solaio in acciaio

_carichi strutturali q_s : massetto in cls, lamiera grecata

_massetto in cls spessore 0,11 m= 2,15 kN/m²

_lamiera grecata tipo HI-BOND spessore 0,7mm = 0,09 kN/m²

_trave IPE330 0,49 kN/m²

_totale q_{s =} 2,73 kN/m²

 

_carichi permanenti q_p : pavimento, allettamento, isolante, incidenza impianti e tramezzi

_pavimento in gres porcellanato 0,015 m * 20 kN/m³ = 0,3 kN/m²

_massetto in cls leggero 0,06 m * 14 kN/m³ = 0,84 kN/m²

_isolante 0,04 m * 0,4 kN/m³ = 0,016 kN/m²

_incidenza impianti 1 kN/m²

_incidenza tramezzi 0,5 kN/m²

_totale q_p = 2,66 kN/m²

 

_carichi accidentali q_A:

_ambiente residenziale 2,00 kN/m²

_totale q_A: 2,00 kN/m²

_totale carichi 7,39 kN/m²

_coefficienti di sicurezza

Per aumentare la sicurezza del dimensionamento ogni carico va moltiplicato per un coefficiente di sicurezza (poco più grande di 1) e questi sono: γ_s = 1,3  γ_p = 1,3  γ_A= 1,5

_totale carichi (con coeff.sicurezza) = 10,01 kN/m²

_calcolo carico distribuito:

q = (q_s * γ_s + q_p  *γ_p+ q_A *γ_A) * i = 10,01 kN/m² * 4 m =

q =40,04 kN/m

_calcolo momento massimo:

M_max = (40,04 kN/m * 6² m²  )/8 =

M_max =180,18 kN * m

_calcolo W_xmin trave (in quanto il parametro della resistenza non ha subito variazioni):

W_xmin= M_max /σ_amm

W_xmin= 180,18 kNm/10³ * 239,13 kN/m²

W_xmin= 0,0007535 m³= 753,5 cm³

È necessario dunque scegliere una IPE superiore, perchè la IPE330 non copre tale valore di modulo di resistenza a flessione, si adotta perciò una IPE 360 ( W_x = 904 cm³).

5.3_ Dati di progetto nella tabella Excel

Nella tabella Excel compaiono nelle varie caselle i vari addendi e fattori che devono essere sommati e moltiplicati fra loro al fine di ottenere il dimensionamento: nella prima riga c’è il dimensionamento della trave senza considerarne il peso proprio, nella seconda invece c’è il dimensionamento che tiene conto anche al peso proprio della trave.

6.3_ Conclusioni

Anche tramite la tabella di Excel è possibile vedere come il calcolo del peso della trave incida anche in questo caso molto sulla scelta della trave, e ancora una volta questo è dovuto dall’elevato peso specifico del materiale. Tuttavia, paragonandolo agli altri due materiali è chiaro come l’acciaio, su una luce di 6m, presenti un’altezza veramente ridotta (circa 15 cm in meno) rispetto alle travi sia di legno che di calcestruzzo, che sono alte uguali (=50 cm).