ESERCITAZIONE 1 - Dimensionamento trave in legno, acciaio e CLS armato

In questa esercitazione dimensioneremo una trave soggetta a momento flettente mediante l'ausilio di un foglio di calcolo; fissata la base della trave come uno degli imput della tabella avremo quindi come output l'altezza minima della trave relativamente agli imput scelti. 

Il metodo verrà illustrato separatamente per travi in tre materiali diversi, rispettivamente legno, acciaio e calcestruzzo armato.

Scelto il solaio in figura, andremo a dimensionare la trave più sollecitata, ovvero quella con l'area d'influenza più grande.

TRAVE in LEGNO (sezione rettangolare)

Per prima cosa definiamo il pacchetto del solaio sostenuto dalla trave in questione ed effettuiamone l'analisi dei carichi.

Moltiplichiamo il peso specifico (KN/m³) di ciascun materiale per il volume (m³) che esso occupa in un metro quadrato (m²) di stratigrafia; ciò che otteniamo è il carico distribuito (KN/m²)

 I primi due elementi sono i carichi permanenti non strutturali (q_p) ai quali aggiungiamo 1 KN/m² per i tramezzi e 0,5 KN/m² per gli impianti (quantità forfettarie da normativa).

q_p = 0,40 + 0,54 + 1 + 0,5 = 2,44 KN/m²

Gli altri tre elementi sono invece i carichi strutturali (q_s)

q_s = 0,84 + 0,12 + 0,11 = 1,07 KN/m²

il terzo tipo di carichi da tenere in considerazione e quello dei carichi accidentali (q_a) relativo alla destinazione d'uso degli ambienti (scegliamo 2 KN/m², valore normato relativo alla destinazione residenziale)

q_a = 2,00 KN/m²

Inseriamo i valori di q_s, q_p e q_a nel foglio di calcolo insieme ai valori precedentemente scelti di interasse (definito dal telaio inizialmente scelto), luce (lunghezza della trave), resistenza a flessione caratteristica (fm,k), coefficiente riduttivo K_mod (riduce i valori di resistenza del materiale tenendo conto sia dell'umidità che della durata del carico gravante sulla struttura)_, il coefficiente parziale di sicurezza relativo al materiale (gamma_m) e la base della trave. 

Descriviamo in breve attraverso quali passaggi il foglio di calcolo giunge al valore di h:

1. determinazione di q (KN/m), dato da (q_s x 1,3 + q_p x 1,3 + q_a x 1,5) x interasse, dove 1,3; 1,3 e 1,5 sono fattori di amplificazione dei carichi
2. determinazione del momento flettente M (KNm) che per una trave appoggiata con carico uniformemente distribuito sappiamo essere pari a ql²/8
3. determinazione della tensione di progetto f_d (N/mm²) data dal prodotto tra la resistenza a flessione caratteristica (fm,k) ridotta dal coefficiente di sicurezza gamma (qui è stato usato quello relativo al legno massiccio, pari a 1,50) e il coefficiente riduttivo K_mod (che, come detto sopra, tiene conto della durata del carico e della classe di servizio del progetto, che a sua volta fissa i valori massimi di umidità del legno a determinate condizioni di temperatura e umidità relativa)
4. determinazione del valore minimo di h (h_min), attraverso la formula di Navier (sig_max = (M/I_x)y_max) ponendo f_d = sig_max e sapendo che y_max è pari ad h/2 e che I_x è pari a bh³/12 per una sezione rettanolare.

Il valore così ottenuto è stato infine ingegnerizzato, ossia va scelto un valore dell’altezza superiore al valore minimo e compatibile con i profili esistenti sul mercato (nel caso del legno è stato approssimato il valore ottenuto al multiplo di 5cm [con 0cm=0] immediatamente più grande di h_min)

Trave in ACCIAIO (IPE)

Per prima cosa definiamo il pacchetto del solaio sostenuto dalla trave in questione ed effettuiamone l'analisi dei carichi.

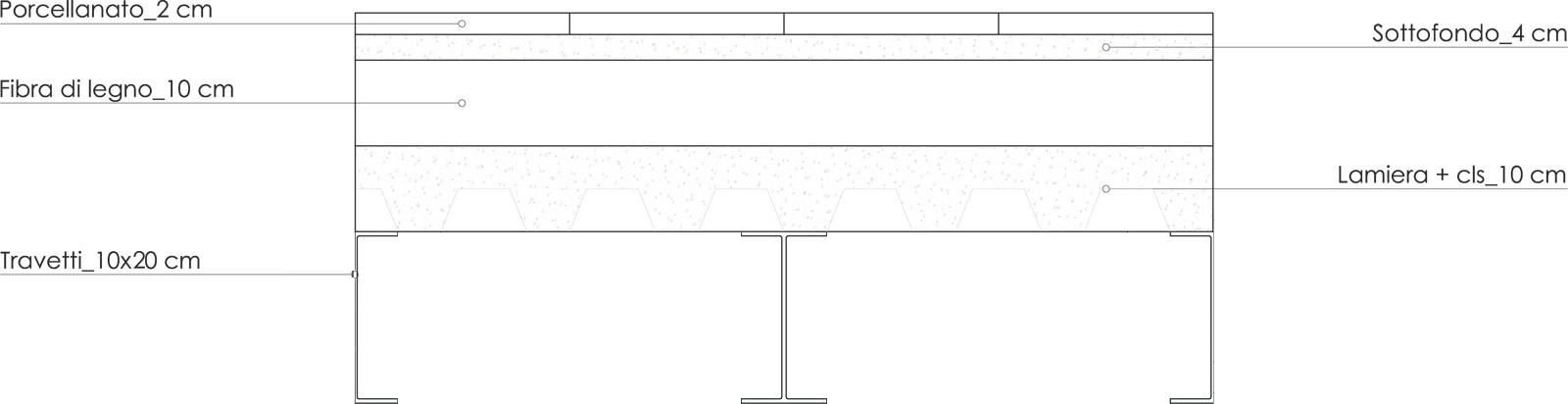
Moltiplichiamo il peso specifico (KN/m³) di ciascun materiale per il volume (m³) che esso occupa in un metro quadrato (m²) di stratigrafia; ciò che otteniamo è il carico distribuito (KN/m²)

I primi tre elementi sono i carichi permanenti non strutturali (q_p) ai quali aggiungiamo 1 KN/m² per i tramezzi e 0,5 KN/m² per gli impianti (quantità forfettarie da normativa).

q_p = 0,32 + 0,72 + 0,23 + 1 + 0,5 = 2,77 KN/m²

Gli altri due elementi sono invece i carichi strutturali (q_s)

q_s = 1,66 + 0,45 = 2,11 KN/m²

il terzo tipo di carichi da tenere in considerazione e quello dei carichi accidentali (q_a) relativo alla destinazione d'uso degli ambienti (scegliamo 2 KN/m², valore normato relativo alla destinazione residenziale)

q_a = 2,00 KN/m²

Inseriamo i valori di q_s, q_p e q_a nel foglio di calcolo insieme ai valori precedentemente scelti di interasse (definito dal telaio inizialmente scelto), luce (lunghezza della trave) e tensione caratteristica di snervamento (f_y,k, individua la resistenza del materiale)

Descriviamo in breve attraverso quali passaggi il foglio di calcolo giunge al valore di h:

1. determinazione di q (KN/m), dato da (q_s x 1,3 + q_p x 1,3 + q_a x 1,5) x interasse, dove 1,3; 1,3 e 1,5 sono fattori di amplificazione dei carichi
2. determinazione del momento flettente M (KNm) che per una trave appoggiata con carico uniformemente distribuito sappiamo essere pari a ql²/8
3. determinazione della tensione di progetto f_d (N/mm²) data dalla tensione caratteristica di snervamento f_y,k ridotta dal coefficiente di sicurezza gamma_s (in questo caso pari a 1,05)
4. determinazione del valore minimo del modulo di resistenza a flessione W_x (W_xmin), attraverso la formula di Navier (sig_max = (M/W_xmin) 
   → W_{xmin =} M/sig_max) ponendo f_d = sig_max.

Il valore così ottenuto (642,19cm³) è stato infine ingegnerizzato, ossia va scelto un profilo esistente sul mercato con valore di W_x immediatamente più grande di W_xmin (nel caso specifico è stata scelta una IPE330 con W_x = 713,0cm³)

Trave in CLS ARMATO (sezione rettangolare)

Per prima cosa definiamo il pacchetto del solaio sostenuto dalla trave in questione ed effettuiamone l'analisi dei carichi.

Moltiplichiamo il peso specifico (KN/m³) di ciascun materiale per il volume (m³) che esso occupa in un metro quadrato (m²) di stratigrafia; ciò che otteniamo è il carico distribuito (KN/m²)

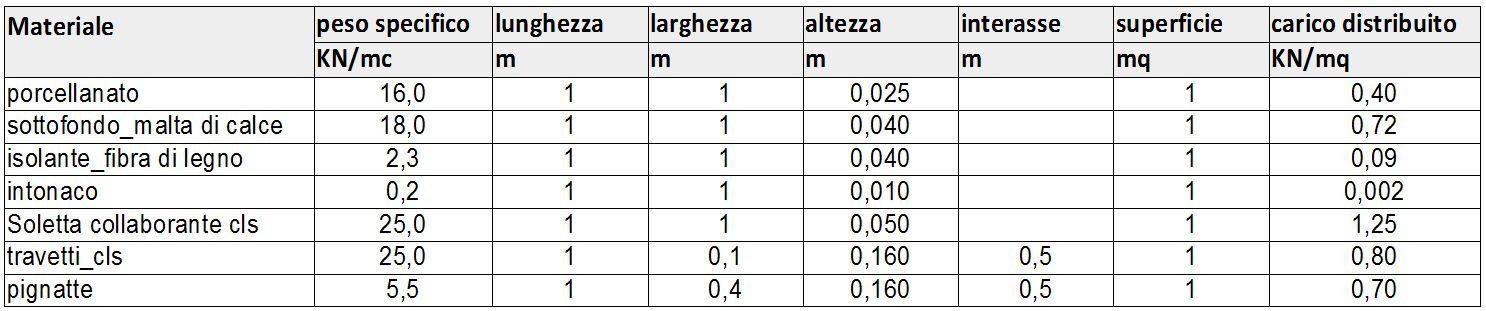
I primi quattro elementi sono i carichi permanenti non strutturali (q_p) ai quali aggiungiamo 1 KN/m² per i tramezzi e 0,5 KN/m² per gli impianti (quantità forfettarie da normativa).

q_p = 0,40 + 0,72 + 0,09 + 0,002 + 1 + 0,5 = 2,71 KN/m²

Gli altri tre elementi sono invece i carichi strutturali (q_s)

q_s = 1,25 + 0,80 + 0,70 = 2,75 KN/m²

il terzo tipo di carichi da tenere in considerazione e quello dei carichi accidentali (q_a) relativo alla destinazione d'uso degli ambienti (scegliamo 2 KN/m², valore normato relativo alla destinazione residenziale)

q_a = 2,00 KN/m²

Inseriamo i valori di q_s, q_p e q_a nel foglio di calcolo insieme ai valori precedentemente scelti di interasse (definito dal telaio inizialmente scelto), luce (lunghezza della trave), resistenza caratteristica del calcestruzzo (f_ck) e dell'acciaio (f_yk), base della trave e delta (distanza tra il baricentro dell'armatura e il filo del calcestruzzo teso)

Descriviamo in breve attraverso quali passaggi il foglio di calcolo giunge al valore di h:

1. determinazione di q (KN/m), dato da (q_s x 1,3 + q_p x 1,3 + q_a x 1,5) x interasse, dove 1,3; 1,3 e 1,5 sono fattori di amplificazione dei carichi
2. determinazione del momento flettente M (KNm) che per una trave appoggiata con carico uniformemente distribuito sappiamo essere pari a ql²/8
3. determinazione della tensione di progetto dell'acciaio f_yd (N/mm²) data dalla tensione caratteristica di snervamento f_y,k ridotta dal coefficiente di sicurezza gamma_s (di valore pari a 1,15 per gli acciai da armatura)
4. determinazione della tensione di progetto del calcestruzzo f_cd (N/mm²) data dalla tensione caratteristica f_ck ridotta dal coefficiente parziale di sicurezza gamma_c (uguale a 1,5) e da un ulteriore coefficiente alfa_cc (coefficiente riduttivo per le resistenze di lunga durata, pari a 0,85)
5. Determinazione di H_min = H_u + delta dove:
   H_min = altezza minima della trave
   H_u = altezza utile della trave, dal filo compresso del calcestruzzo al baricentro dell'armatura tesa 
   attraverso la formula inversa del momento flettente esterno dato dalla coppia interna T=-C per il loro braccio Txb*=Cxb* dove:
   T = A_f x f_yd
   A_f = area delle armature tese
   b*= H_u - X_c/3 (altezza della risultante delle forze determinanti compressione)
   C = (f_cd x b x X_c/2)
   X_c = altezza della sezione compressa. Per il metodo dei triangoli simili definisco:
                                            X_c = {H_u x [f_cd/(f_cd+(f_yd/n))]}

   dove definisco: (f_cd/(f_cd+(f_yd/n))) = beta dove:
   n=15 (valore normato; rappresenta il coefficiente di omogeneizzazione dato dal diverso      comportamento elastico dell'acciaio e del calcestruzzo ed è definito da E_s/E_c=10, da    normativa ampliato del 50%)
   Dunque:
                                                          M=Cxb*
   M=(f_cd x b x X_c/2) x (H_u - X_c/3) 
   M=[f_cd x b x (H_u x beta)/2] x [H_u - (H_u x beta)/3]
   M=[f_cd x b x (H_u x beta)/2] x (1 - beta/3)H_u
   M=(f_cd x b x beta/2) x (1 - beta/3)H_u²
                                  H_u = (M/b)^1/2 x {2/[f_cd(1-beta/3)beta]^1/2}

   ^{dove definisco:} {2/[f_cd(1-beta/3)beta]^1/2} = r 

   quindi:                                           H_u = (M/b)^1/2 x r
    

Trovata finalmente l'altezza minima (H_min = H_u + delta) della trave, riverifico la sua sezione comprendendo tra i carichi strutturali anche il carico lineare della trave stessa moltiplicato anch'esso per il relativo fattore di amplificazione dei carichi - 1,3 (carico determinato nelle ultime due colonne della prima riga della tabella moltiplicando l'area della sezione per la massa volumica del calcestruzzo).

Nella seconda riga della tabella si svolgono automaticamente gli stessi calcoli della prima, ma con il carico lineare maggiorato. Se la nuova H_min risulterà minore dell'H ingegnerizzata scelta (approssimando il valore ottenuto al multiplo di 5cm [con 0cm=0] immediatamente più grande di h_min), allora il calcolo della sezione della trave sarà verificato!