Esercitazione n°4 | Calcolo del centro di rigidezza

La prima parte della quarta esercitazione analizza e mette al confronto il comportamento di una struttura simmetrica, sia dal punto di vista geometrico, che da quello meccanico, con una struttura simmetrica solo dal punto di vista geometrico.

STRUTTURA SIMMETRICA SIA GEOMETRICAMENTE CHE MECCANICAMENTE

La struttura costituita da travi e pilastri è vincolata a terra mediante degli incastri (FIG.01), le travi invece sono collegate ai pilastri con cerniere interne (FIG.02) e l'impalcato è rigido, in grado di ruotare solo intorno all'asse z (FIG.03).

Una volta che abbiamo assegnato la sezione (quindi anche il materiale) alle travi e ai pilastri, applichiamo una forza orizzontale pari a 100kN nel centro geometrico della struttura, che corrisponde anche al centro meccanico, poichè tutti i pilastri hanno la stessa rigidezza k=12EI_x/h³.

Dato che la forza è applicata sull'asse centrale delle rigidezze vi sarà una traslazione u che per la legge di Hooke è pari a u= F/k. (FIG.04) 

F=100/3 kN= 33,33

k= 12 24855578 0,000675/ 27=7456,67 KN/m

u= 33,33kN/7456,67 kN/m = 0,0045 m

STRUTTURA SIMMETRICA SOLO GEOMETRICAMENTE

La struttura in FIG.06 resta simmetrica da un punto di vista geometrico, ma non lo è più dal punto di vista meccanico poichè la rigidezza, che dipende dal momento di inerzia della sezione, è maggiore nei pilastri rossi rispetto alla rigidezza dei pilastri blu. Ciò comporta uno spostamento dell'asse delle rigidezza verso i pilastri rossi; in questo modo la forza non è più applicata nel centro delle rigidezze e ciò determina un momento esterno generato dalla forza orizzontale F.

La deformata  di questa struttura non sarà il risultato di una sola traslazione, ma dell'azione congiunta di una traslazione ed una rotazione (FIG.07).

Intuitivamente immaginiamo che i pilastri più rigidi sviluppano una reazione vincolare più grande e di conseguenza assorbono una quantità maggiore della F ( =100kN) iniziale. Per sapere effettivamente come si riparte la forza nei diversi controventi, consideriamo la loro rigidezza k=12EI_x/h³. A parità di materiale (E) e di altezza del pilastro (h), il rapporto k₁/k₂ = I₁/I₂ 

I₁=0,000675

I₂=0,0052

I₁=0,13 I₂

_k1=0,13 k₂

F = 2 k₁ u + 1 k₂ u

F= u(0,26 k₂ + 1k₂)

F= 1,26k₂ u 

u= F/1,26k₂

F₁= 0,13 k₂ (F/1,26k₂)= 10,32 kN

F₂= k₂ (F/1,26k₂)= 79,36 kN

2F₁+1F₂=100kN

Perciò il telaio, con pilastri aventi sezione 50x50, si farà carico di quasi 4/5 della forza iniziale F, mentre agli altri telai, con pilastri aventi sezione 30x30, arriverà solo 1/10 della F iniziale.

La struttura in FIG.06 subisce la duplice azione di una traslazione e di una rotazione. Ciò è dovuto al fatto che il centro delle rigidezze non coincide più con i centro gerometrico della struttura.

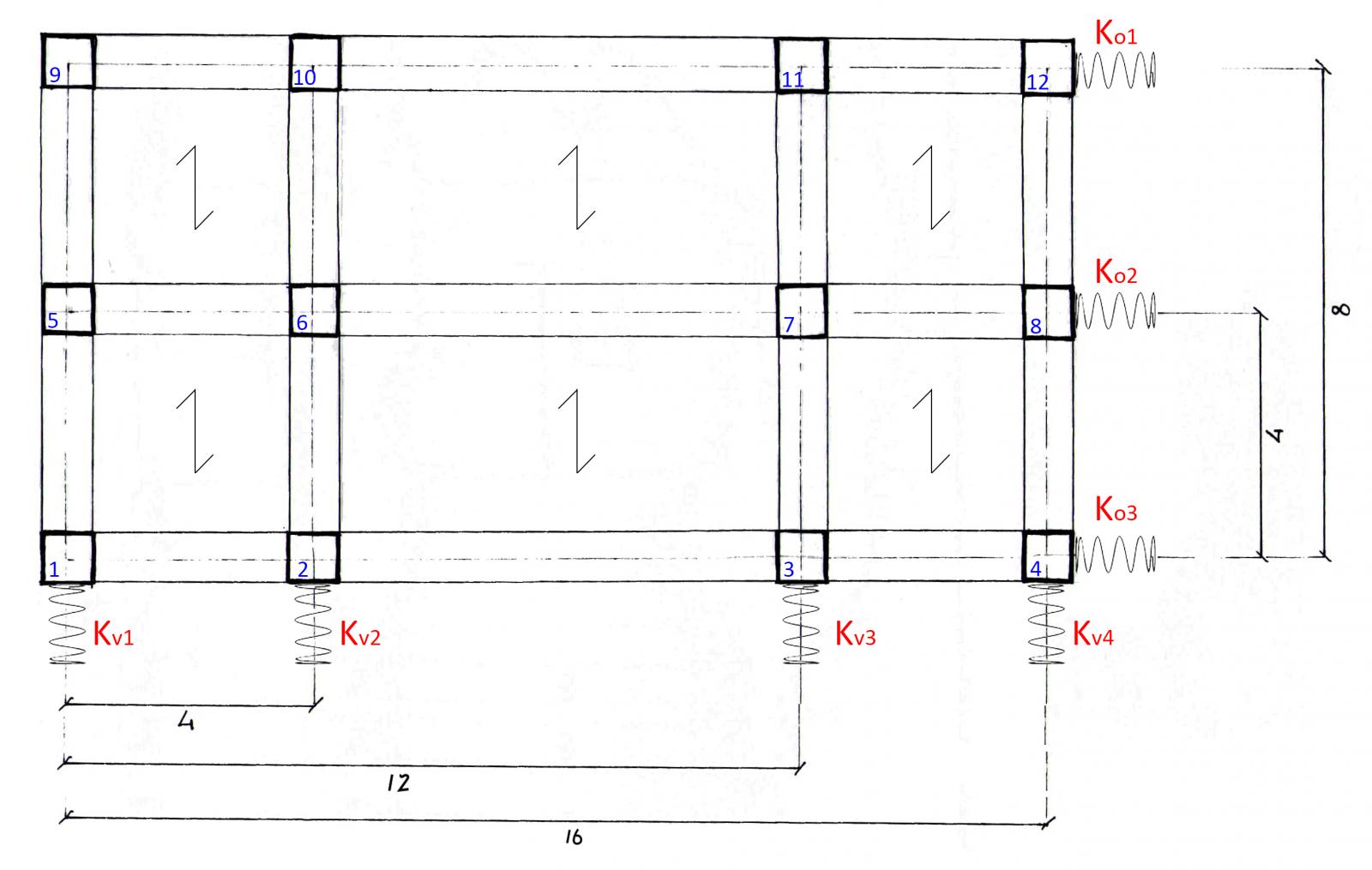FIG.08

Lo schema delle rigidezze della FIG.08 ed un foglio di calcolo Excel ci aiuteranno a calcolare la posizione precisa del centro delle rigidezze. 

STEP 1 | Sono stati individuati i telai che svolgono la funzione di controventi, i pilastri e le loro caratteristiche: E definito dal materiale, I definito dalla sezione, h l'altezza del pilastro. 

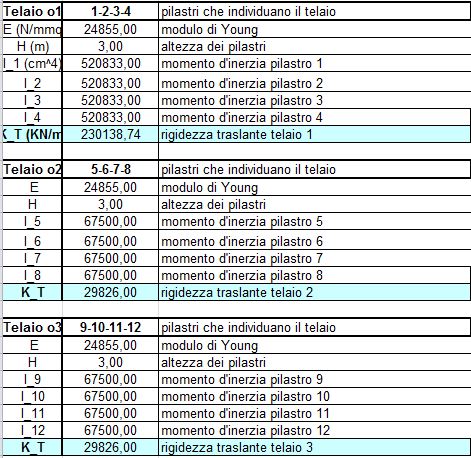
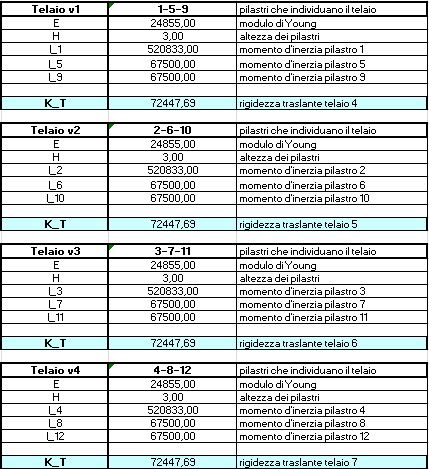   FIG.09

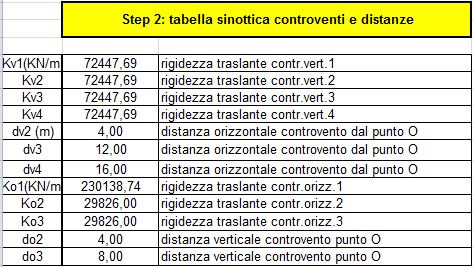
STEP 2 | La tabella sinottica dei controventi e delle distanze indica quali sono i valori delle rigidezze di ogni talaio e la distanza di questo da un punto di origine arbitrariamente stabilito. In questo caso in corrispondenza del pilastro 1. 

STEP 3 | Si è voluto analizzare la struttura precedentemente studiata per le esercitazioni precedenti, che presenta una geometria molto semplice. Per questo motivo la ricerca del centro di massa non è particolarmente complicata. Nel caso in cui la struttura avesse presentato geometri più complesse, sarebbe stato necessario scomporre l'area iniziale in aree di base assimilabili a figure semplici, come ad esempio rettangoli, considerando il centro di ognuna di queste aree.  

CdM (  8  ;  4  )

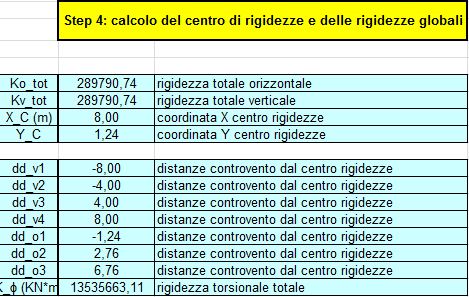
STEP 4 | Per calcolare le coordinate del centro delle rigidezze è necessario moltiplicare la rigidezza di ogni telaio (orizzontale prima e verticale poi) per la distanza di questo dall'origine degli assi e una volta sommati tutti i valori ottenuti, si divide per la rigidezza totale (orizzontale prima e verticale poi). Una volta note le coordinate del centro delle rigidezze è facile ricavare la distanza di ogni controvento da questo.

Il centro delle rigidezze ha ascissa pari a quella del centro di massa perchè i controventi verticali presentano tutti e 4 la stessa rigidezza.

CdR (  8  ; 1,24  )

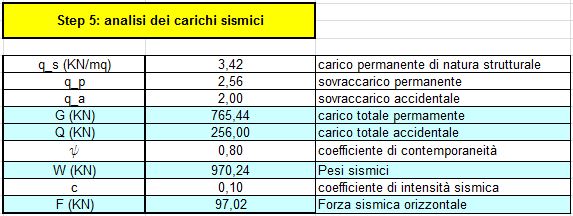
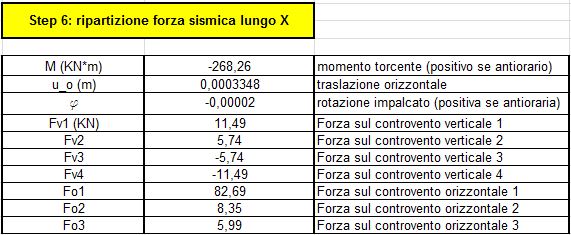
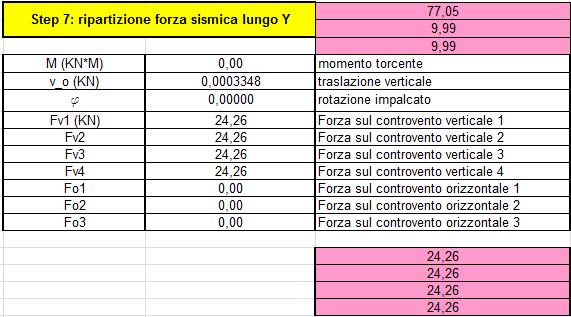
STEP 5-6-7 | Dai carichi permanenti ed accidentali si ricava la forza sismica orizzontale (STEP 5), che potremmo avere sia nella direzione x (STEP 6) che nella direzione y(STEP 7). Possiamo notare come la forza sismica lungo y sia completamente assorbita dai controventi verticali e come i controventi orizzontali non svolgano nessun ruolo particolare nei confronti di questa forza. Ciò è dovuto al fatto che il centro delle rigidezze ha in comune con il centro di massa l'ascissa, e così nel caso in cui la forza sismica arrivi lungo y la struttura traslerebbe senza ruotare.

                 Forza lungo y applicata nel centro di rigidezza             

                Forza lungo y applicata nel centro di massa  

                 Forza lungo y applicata nel centro di rigidezza

                 Forza lungo y applicata nel centro di massa