TERZA ESERCITAZIONE

In questa esercitazione, l'obbiettivo è quello di comprendere come gli sbalzi siano parti della struttura che richiedono un'approfondimento maggiore, dato che rappresentano  dei punti critici.

Il solaio preso in eseme e qui riportato:

FIG.1

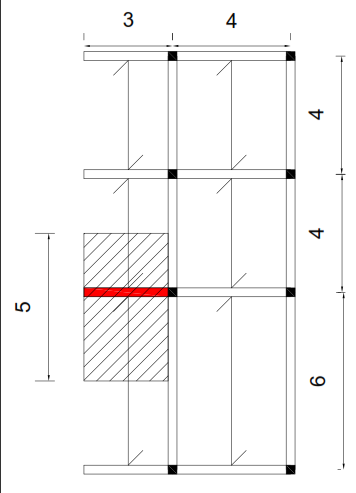
La trave in rosso, sarà la trave che andremo a dimensionare, poichè è quella a sbalzo con una maggior area d'influenza.

Area d'influenza= 15 mq 

Trave acciaio:

Il solaio preso in esame è cosi composto:

FIG.2

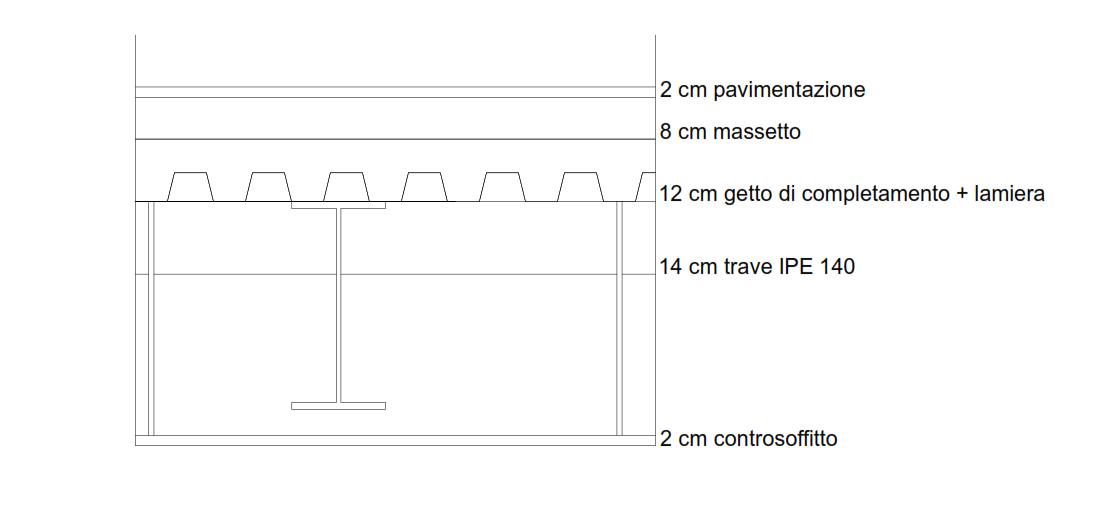
Pavimentazione: con piastrelle di 20cmx 20 cm hanno un pso di 0.31kn/mq

Massetto: calcestruzzo alleggerito 8 cm, il peso 16 kn/mc

Getto di completamento: area di 0.0953 mq con un peso specifico di 25kn/mc

Lamiera grecata: peso di 0.2 kn/mq

Travi: IPE area di  16,4 cmq e peso specifico di 78.5 kn/mc

Controsoffitto: 2 cm 0,26kn/mq

Dopo aver diviso i carichi in strutturali e carichi permanenti tenendo anche conto dei tramezzi e degli impianti come da normativa li vado ad inserire nella tabella excel, in cui aggiungo anche i carichi accidentali che per civili abitazioni si prende il valore di 2 kn/mq.

FIG.3

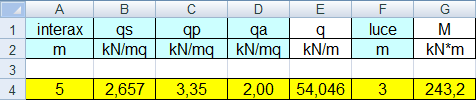
Mmax calcolato è analogo a quello calcolato nell'esercitazione precedente, ma in questa la luce è esattamente la metà.

Il momento di una mensola con un carico uniforme è max all'incastro e quivale a ql²/2, mentre quello di una trave appoggiata è max in mezzeria e quivale a ql²/8.

Dopo aver inserito i valori nella tabella trovo il Wx 1017,04 cmc e cerco un valore di Wx maggiore a quello trovato, scelgo 1160 cmc che corrispone a un IPE 400, si aggiunge poi il momento d'inerzia corrisponedente.

FIG.4

L'abbassamento Vmax è 0.972 cm 

il rapporto luce/ abbassamento è maggiore di 250 quindi è verificata.

La verifica a deformabilità è soddisfatta.

Solaio in calcestruzzo armato:

il solaio è cosi suddiviso:

Fig.5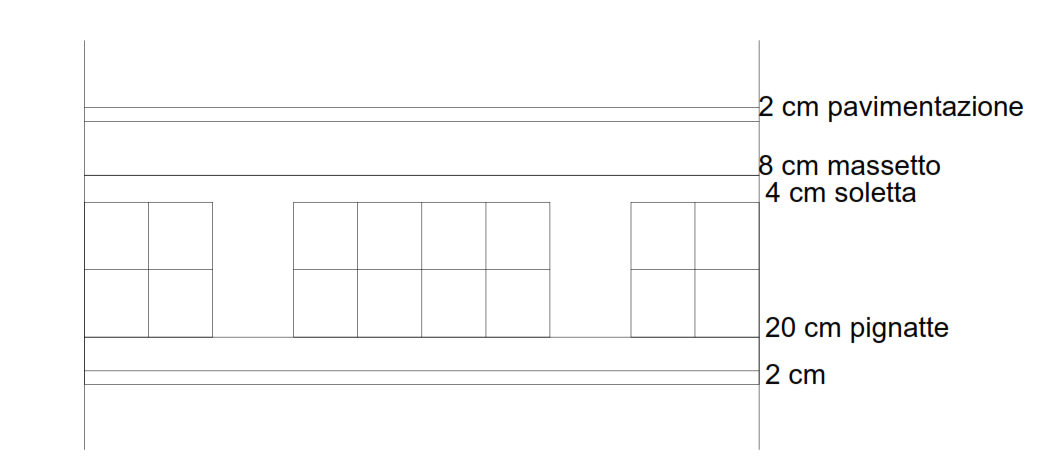

Solaio in calcestruzzo armato:

il solaio è cosi composto

Pavimentazione: 2cm peso di 0,31 kn/mq

Massetto 8 cm peso 1,28 kn/MQ

Soletta 4 cm peso 1 kn/mq

Travetti 12cm x 20 cm=2 numero travetti x0,12x0,2x25kn/mc=1,2kn/mq

Pignatta ne ho 8 in un m peso 0,768 kn /mq

Controsoffitto 2cm 0,26kn/mq

Si suddividono i carichi strutturali, permanenti e accidentali, tenendo conto anche dei tramezzi e degli impianti.

Una volta analizzati i carichi si inseriscono nella tabella excel.

Fig.6

Come si può notare Mmax ha un valore molto vicino a quello dell'esecitazione precedente ma è necessario ricordare che in questo caso la luce è la metà.

Una volta stabilita la base di 20 cm, il copriferro, il modulo elstico e l'H ingegnerizzata, il programma ci calcolerà l'abbassameto Vmax, che corrispone a 0,74 cm.

Il rapporto luce/abbassamento è maggiore di 250, quindi la verifica a deformabilità è soddisfatta.

Proviamo ora a vedere se la verifica è soddisfatta utilizzando la stesssa trave, ma con la base di 30 cm.

FIG.7

In questo caso la verifica non è soddisfatta.

Riprendiamo ora la prima trave verificata quella con la base di 20 cm e vediamo se aumentando di 1 m la luce la trave resta comunque verificata.

FIG.8

Ma come si può notare anche in questo caso la verifica non è soddisfatta.

Solaio in legno:

Procediamo con la verifica di un solaio in legno cosi suddiviso:

FIG.9

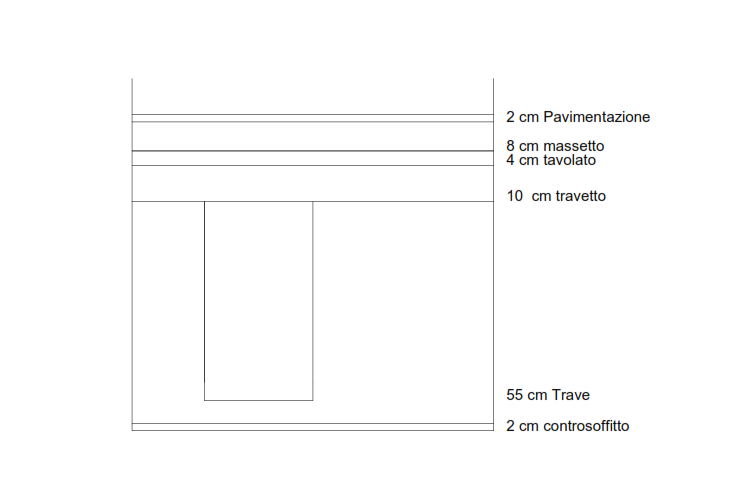
Paviemntazione: 2cm peso 0,31kn/mq

Massetto: 8 cm peso 1,28 kn/mq

Tavolato: legno abete 4 cm peso 0,18 kn /mq

Travetto: legno lamellare abete 10 cm per 8 cm ne ho 2 in 1m peso 0,72 kn /mq

Controsofitto: 2 cm peso 0,26 kn /mq

Una volta eseguita l'analisi dei carichi si procede suddividendoli in carichi strutturali, permanenti e accidentali tenendo conto anche del contributo dei tramezzi e degli impianti.

Una volta calcolati tutti i carichi si inseriscono nella tabella excel.

FIG.10

Calcoliamo il peso della trave 

base x altezza =30 cm x 65=1950 cmq= 0,195 mq x 3 che è la luce= 0,585 mc (volume)

peso della trave 0,8775 kn/mq

Si inserisce poi il peso della trave nei carichi q.

L'abbassamento Vmax corrisponde a 0,86 cm.

Il rapporto luce/ abbassamento è maggiore di 250 quindi la verifica è soddisfatta.