blog di sharon.pavoncello

L'esercitazione 3 prevedeva il dimensionamento di una trave a sbalzo, nelle 3 diverse tecnologie: Legno, Acciaio e Cemento armato.

Questo è il telaio preso in esame:

Fig.1

Fig.2

La luce= 3 m

Interasse= 4,5 m

Riprendo lo studio dei 3 solai fatto nell'esercitazione 1 e riporto qui sotto solo i carichi calcolati.

LEGNO:

CARICHI STRUTTURALI: qs

Travetto:  0.056 kn/mq

Tavolato:0,21 kn/mq

qs=(0,056+0,21) kn/mq =0,266 kn/mq

CARICHI PERMANENTI:

Pavimento: 0,2 kn/mq

Massetto: 0,72 kn/mq

Controsoffitto: 0,26 kn/mq

Tramezzi: 1 kn/mq

Impianti: 0,5 kn/mq

isolante: 0,008 kn/mq

qp=(0,2+0,72+0,26+1+0,5+0,008)kn/mq =2,688 kn/mq

CARICHI ACCIDENTALI:

Per residenze da normativa 2 kn /mq

Per uffici  da normativa 3 kn /mq

Vado ad inserire i valori appena citati nella file excel:

Il foglio excel mi calcola q_u  considerando i relativi coefficenti di sicurezza 1,3 per i carichi struttuali e 1,5 per i carichi permaneti e accidentali.

Trattandosi di una trave a sbalzo, M_max si calcola M_max=q_u l²/2

 inserisco ora i dati relativi al materiale ossia quello di un legno classe C24 (f_mk = 24 N/mm², K_mod = 0.8, γ_m  = 1.50) per ottenere un valore della tensione di progetto pari a f_dC = 12,8 N/mm² 

 scelgo una base di 25 cm ed ottengo una altezza minima  di 52,96 cm che ingegnerizzo a 55 cm

Ho così dimensionato una trave di base 25 cm e altezza 55 cm 

Nel caso della mensola dopo aver dimensionato la sezione, devo fare la verifica a deformabilità.

La verifica si effettua allo SLE (Stato Limite di Esercizio),poichè la verifica ha l'obbiettivo di verificare che le deformazioni siano limitate e che non compromettono il normale utilizzo della struttura.

Calcolo tramite il  foglio excel q_e  attraverso l'utilizzo di questa formula:

q_e=(G₁₊G₂+0,5x Q₁)xi=

In questo caso,non considero il peso proprio della trave, poichè il legno è un materiale leggero.

Aggiungo il valore del  modulo elastico pari a E = 8000 N/mm² ed ottengo  Ix 

Posso ora calcolare l'abbassamento massimo, che è pari a :

v_max=q_e l⁴/8Ei_x

nel mio caso l'abbassamento corrisponde a 0,65 cm 

Non mi resta che verificare che il rapporto tra la luce della trave e il suo spostamento massimo sia maggiore di 250 come da normativa.

l/v_{max >} 250

l/v_max= 461,06

quindi la trave è verificata!!!!

ripeto lo stesso esercizio più volte cambiando dei parametri, riporto qui di seguito i risultati:

ACCIAIO:

Il solaio preso in esame è composto dai seguenti carichi:

CARICHI STRUTTURALI: qs

Lamiera:  0.11 kn/mq

Getto di completamento :2,4  kn/mq

Trave secondaria: 0,16 kn/mq

qs=(0,1+ 2,4+0,16 ) kn/mq = 2,67  kn/mq

CARICHI PERMANENTI:

Pavimento: 0,2 kn/mq

Massetto: 0,72 kn/mq

Controsoffitto: 0,26 kn/mq

Tramezzi: 1 kn/mq

Impianti: 0,5 kn/mq

isolante: 0,008 kn/mq

 

qp=(0,2+0,72+0,26+1+0,5+0,008)kn/mq =2,688 kn/mq

 

CARICHI ACCIDENTALI:

Per residenze da normativa 2 kn /mq  

oppure per uffici da normativa 3 kn/mq

vado ad inserire tali valori nel foglio excel e trovo il valore di q_{u =} 47,27 kn/m

Inserendo il valore della luce dello sbalzo mi calcolo M_max= 212,746

 Ho scelto un acciaio di classe S235 che ha come  tensione caratteristica un valore  pari a  fyk=235 N/mm²

 trovato il valore di fd = 223,81 N/mm² calcoliamo il modulo di resistenza a flessione minimo uguale a Wx,min = 950,57 cm³

 vado poi  a consulatare la tabella dei profilati IPE e scelgo un IPE con W_x maggiore di quello trovato.

f_d=223,81 N/mm²    

W₂=950,57 cm³

Trave IPE 400

 Inserisco il valore di I_x  ricavato dalla tabella I_x =23130 cm⁴  

Questa volta devo tener conto del peso proprio della trave che nel mio caso corrisponde a 0,66 Kn/m

Mi calcolo q_e  come avevo fatto in precedenza con il legno.

 qe= 29,28 KN/m  mi rendo conto che anche  in questo caso il progetto  è verificato poichè lo spostamento è uguale a v_max =0,610  e quindi il rapporto  I_x/ v_max >250

La trave è verificata!!!

Ripeto la stessa operazione sostituendo al carico accidentale 3 Kn /mq

Anche in questo caso la trave è verificata!!!!!!

CEMENTO ARMATO:

Il solaio che si sta studiando è formato da tali carichi

CARICHI STRUTTURALI: qs

Pignatte :  0.72 kn/mq

Travetti :0,8   kn/mq

Soletta : 1 kn/mq

qs=(0,72+ 0,8+1 ) kn/mq = 2,52 kn/mq

 

CARICHI PERMANENTI:

Pavimento: 0,2 kn/mq

Massetto: 0,72 kn/mq

isolante: 0,008 kn/mq

intonaco : 0,3 kn/mq

Tramezzi: 1 kn/mq

Impianti: 0,5 kn/mq

 

qp=(0,2+0,72+0,3+1+0,5+0,008)kn/mq =2,72888 kn/mq

 

CARICHI ACCIDENTALI:

Per residenze da normativa 2 kn /mq

Compilo la prima parte del foglio Excel con lo stesso metodo delle analisi precedenti e inserisco il valore dello sbalzo trovando così il valore del momento massimo 

Mmax= 209,95 KN*m

 Scelgo un acciaio di classe S450 ( f_yk = 450 N/mm², f_yd = 391.30 N/mm² )

Prendo un cls che abbia come tensione caratteristica f_ck = 30  N/mm² 

In questo modo trovo 3 valori:

f_cd=17N/mm²

 β=0.39

r=2.42

Stabilisco la base   b = 30 cm e il  copriferro di 5 cm e trovo una altezza minima h_min=54,02 cm che vado ad  ingegnerizzare, H=55 cm.

Ripetendo calcoli analoghi a quelli fatti per il legno e acciaio trovo che la trave è verificata a deformabilià.

ma non ho ancora tenuto conto del peso proprio della trave.

Quando il foglio excel tiene conto anche del peso proprio della trave, la verifica non è soddisfatta.

Provo ora ad aumentare l'H della trave e rifaccio la verifica.

Stabilendo un altezza pari a H=60 cm 

la trave è verificata!!!!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

La seconda esercitazione prevedeva la realizzazione su sap di una travatura reticolare in 3d e poi il dimensionamento di essa.

La travatura reticolare è stata fatta  con l’obbiettivo di impiegare strutture sempre più leggere per superare luci sempre più grandi.

 

A  questo punto inizio a lavorare sul foglio excel.

Questo file ha alcuni valori che non sono importanti al fine del dimensionamento così inizio a cancellare i dati che non mi servono.

Lascio solo i valori relativi allo sforzo normale e quelli relativi alla lunghezza delle aste.

Posso procedere ad un'ulteriore pulizia, ordinando in modo crescente la luce delle aste cancello tutte le luci diverse da 2 m (che è la luce delle aste normali) e  da 2,82843 m (che corrisponde alla luce delle diagonali   l*radice di 2).

Quindi ho 2 lunghezze di aste

L= 2m

L=2,82843

Ordinando lo sforzo normale posso distinguere quelle a trazioni, da quelle a compressione e le vado a inserire in un altro file excel per fare il dimensionamento.

TRAZIONE:

Inserisco i valori di N positivi dal più piccolo al più grande   nel file excel  per il dimensionamento.

Scelgo  f_yk (coefficiente caratteristico di snervamento) pari a 235 Mpa  e y_m (coefficiente di sicurezza) pari a 1,05.

Il foglio excel ci calcola  la tensione di progetto f_d e l'area minima A_{_min ,} che poi andrà ingegnerizzata.

Devo ora cercare nei profili standard un valore dell'area maggiore dell'area minima calcolata con excel.

 

Questa operazione andrebbe ripetuta per ogni asta.

Nel mio caso ho ordinato le aste secondo l'area minima e le ho divise in 5 gruppi , in questo modo ho utilizzato 5 tipi di profilati diversi.

Riporto qui sotto le aste maggiormente sollecitate per ogni gruppo e il relativo profilo utilizzato.

Compressione:

Inserisco i valori negativi di N

Do un valore a  f_yk (coefficiente caratteristico di snervamento) pari a 235 Mpa e a  y_m (coefficiente di sicurezza) pari a 1,05.

​Il file calcola , oltre alla tensione di progetto f_d e l'area minima A_{_min} , anche I_{_min}  e rho_min . Dovrò dunque ingegnerizzare tutti e tre i valori, individuandolo nella tabella dei profili standard.

Dovrei ripetere l'operazione per ogni asta.

Anche qui ho deciso di dividere le aste in 5 gruppi, stando attenta di mettere nello stesso gruppo quelle con area e caratteristiche simili.

Riporto qui di seguito il dimensionamento dell'asta più solleciatata per ogni gruppo.

 

 

 

 

 

 

 

La prima esercitazione prevede il dimensionamento della trave maggiormente sollecitata del telaio , nelle tre diverse tecnologie: legno, acciaio e cemento armato.

Fig.1

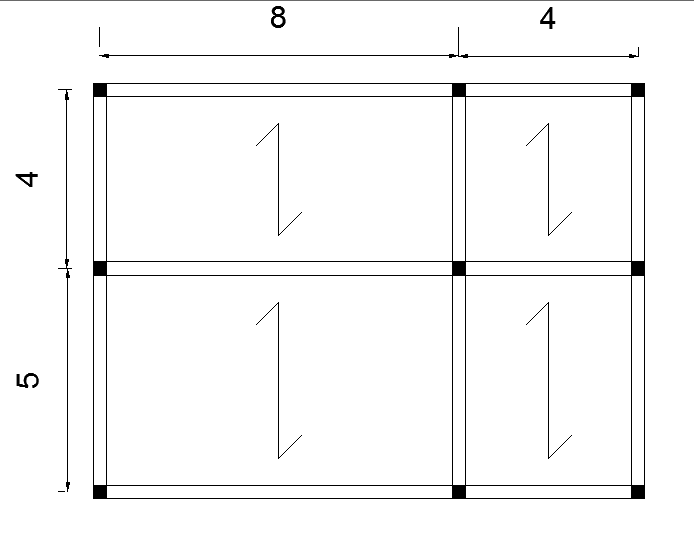
Fig.2

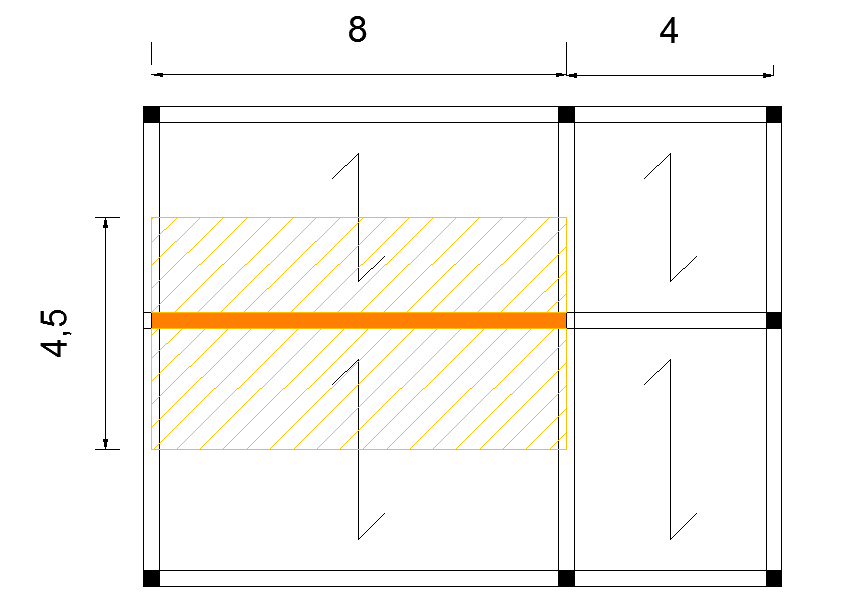
La trave presa in esame è quella colorata in arancio.

interasse di 4,5 m

luce 8m

Legno:

Il solaio preso in esame è cosi composto:

Fig.3

Pavimento: in gres porcellanato spesso 1 cm, peso specifico 20 kn/mc

(0.01x1x1)mc/mq x 20 kn/mc = 0,2 kn/mq

Massetto:  spesso  4cm peso specifico 18 kn/mc

(0.04x1x1)mc/mq x 18 kn/mc = 0,72 kn/mq

Isolante:  spesso 4 cm, poliuretano  espanso peso specifico 0,2 kn/mc

(0.04x1x1) mc/mq x 0,2 kn/mc = 0,008  kn/mq

Tavolato: spesso 3,5 cm peso  0,21 kn/mq

Travetto: in legno lamellare di dimensioni 15 x 16 cm

Peso specifico 3,73 kn/mc

(0.15x1x1)mc/mq x 3,73  kn/mc = 0,056  kn/mq

Controsoffitto :  spessore 2 cm

Peso specifico 13  kn/mc

(0.02 x1x1)mc/mq x 13  kn/mc = 0,26  kn/mq

 

CARICHI STRUTTURALI: qs

Travetto:  0.056 kn/mq

Tavolato:0,21 kn/mq

qs=(0,056+0,21) kn/mq =0,266 kn/mq

CARICHI PERMANENTI:

Pavimento: 0,2 kn/mq

Massetto: 0,72 kn/mq

Controsoffitto: 0,26 kn/mq

Tramezzi: 1 kn/mq

Impianti: 0,5 kn/mq

isolante: 0,008 kn/mq

 

qp=(0,2+0,72+0,26+1+0,5+0,008)kn/mq =2,688 kn/mq

 

CARICHI ACCIDENTALI:

Per residenze da normativa 2 kn /mq

Vado ora ad inserire tali valori nella tabella exel, che terrà conto anche dei coefficienti, (pari a 1,3 per i carichi permanenti strutturali e non strutturali, 1,5 per i carichi accidentali)  per aumentare il peso in modo da garantire una maggiore sicurezza.

Inserendo inoltre il valore della luce e dell’interasse posso facilmente determinare l ‘M max che per le travi doppiamente appoggiate, corrisponde q(lxl)  /8

Scelgo la base di 35 cm e mi ricavo un altezza min di 58,64 cm che imposto di 65 cm poiché non ho ancora considerato il peso della trave.

Fig.4

Ora devo calcolare il peso proprio della trave e verificare che la trave imposta sia verificata

P= (0,35x 0,65x1)mc/m x 7 kn/mc = 1,5925 kn /m

Fig.5

Fig.6

 

 

La trave scelta di 35 cm di base per 65 cm di altezza

é verificata !

Acciaio 

Il solaio da verificare è cosi suddiviso:

Fig. 7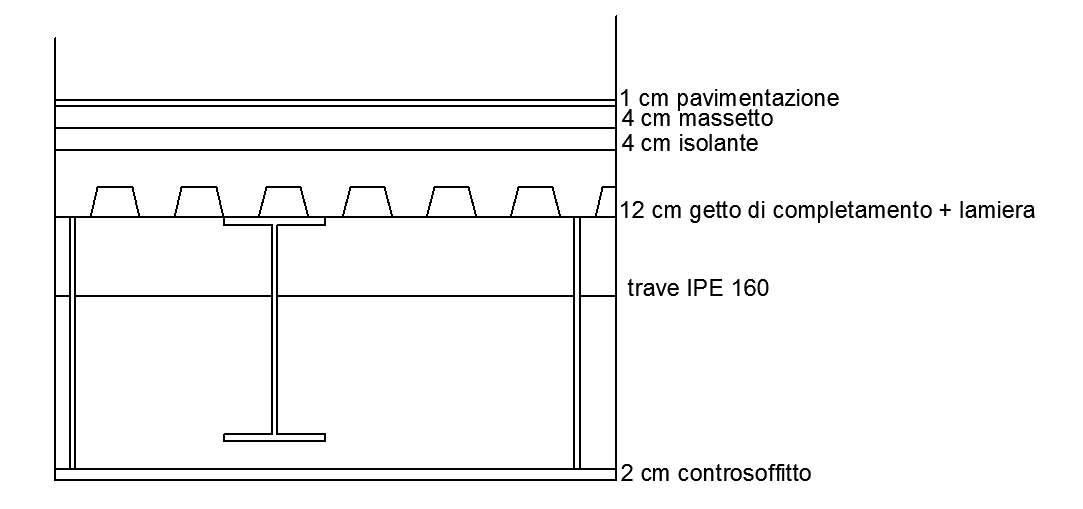

Pavimento: in gres porcellanato spesso 1 cm, peso specifico 20 kn/mc

(0.01x1x1)mc/mq x 20 kn/mc = 0,2 kn/mq

Massetto:  spesso  4cm peso specifico 18 kn/mc

(0.04x1x1)mc/mq x 18 kn/mc = 0,72 kn/mq

Isolante:  spesso 4 cm, poliuretano  espanso peso specifico 0,2 kn/mc

(0.04x1x1) mc/mq x 0,2 kn/mc = 0,008  kn/mq

Massetto di completamento : calcolo l’ area  0,0935

(0.0935x1)mc/mq x 25kn7mc= 2,4 kn/mq

Lamiera grecata

0.11 kn/mq

Trave secondaria: trave IPE 160

Area 20,09 cmq

(0.002009 x1)mc/mq x 78,5 kn7mc=  0,16  kn/mq

Controsoffitto :  spessore 2 cm

Peso specifico 13  kn/mc

(0.02 x1x1)mc/mq x 13  kn/mc = 0,26  kn/mq

 

CARICHI STRUTTURALI: qs

Lamiera:  0.11 kn/mq

Getto di completamento :2,4  kn/mq

Trave secondaria: 0,16 kn/mq

qs=(0,1+ 2,4+0,16 ) kn/mq = 2,67  kn/mq

CARICHI PERMANENTI:

Pavimento: 0,2 kn/mq

Massetto: 0,72 kn/mq

Controsoffitto: 0,26 kn/mq

Tramezzi: 1 kn/mq

Impianti: 0,5 kn/mq

isolante: 0,008 kn/mq

 

qp=(0,2+0,72+0,26+1+0,5+0,008)kn/mq =2,688 kn/mq

 

CARICHI ACCIDENTALI:

Per residenze da normativa 2 kn /mq

Fig.8

 

Inserendo i valori nella tabella exel trovo un Wx min = 1443,69 cmc

Fig.9

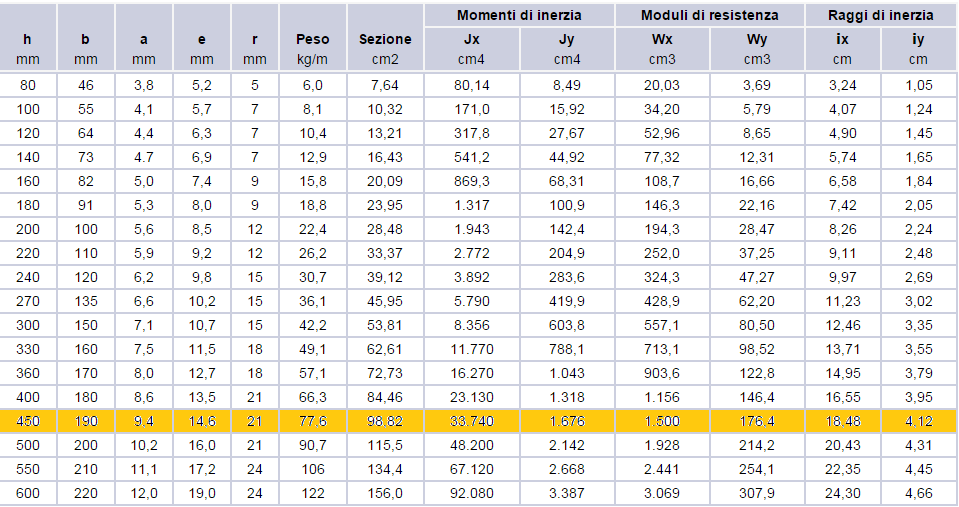
utilizzo IPE 450 

sezione 98,82 cmq

Wx=1500

peso specifico acciaio = 78,5 kn/mc

Calcolo il peso della trave:

P= (0.00988x1)mc/m x 78,5 kn/mc 

P= 0,77 kn/m

Fig.10

Fig.11

 

La trave IPE 450 

é verificata 

Calcestruzzo 

Fig.12

 

Pavimento: in gres porcellanato spesso 1 cm, peso specifico 20 kn/mc

(0.01x1x1)mc/mq x 20 kn/mc = 0,2 kn/mq

Massetto:  spesso  4cm peso specifico 18 kn/mc

(0.04x1x1)mc/mq x 18 kn/mc = 0,72 kn/mq

Isolante:  spesso 4 cm, poliuretano  espanso peso specifico 0,2 kn/mc

(0.04x1x1) mc/mq x 0,2 kn/mc = 0,008  kn/mq

Pignatte :  sono di 16 cm x 40 cm per 25 cm di spessore quindi in un metro ce ne sono 8

Peso totale 0,72 kn/mq

Soletta :  Peso specifico 25  kn/mc

(0.04x1x1)mc/mq x 25   kn/mc = 1 kn/mq

Travetti: 16 x 10 cm

(0.16x1x1)mc/mq x 25   kn/mc = 0,4  kn/mq

Ce ne sono 2 quindi il peso = 0,8kn/mq

Intonaco :  spessore 1,5 cm

Peso 0,3  kn/mq

 

CARICHI STRUTTURALI: qs

Pignatte :  0.72 kn/mq

Travetti :0,8   kn/mq

Soletta : 1 kn/mq

qs=(0,72+ 0,8+1 ) kn/mq = 2,52 kn/mq

 

CARICHI PERMANENTI:

Pavimento: 0,2 kn/mq

Massetto: 0,72 kn/mq

isolante: 0,008 kn/mq

intonaco : 0,3 kn/mq

Tramezzi: 1 kn/mq

Impianti: 0,5 kn/mq

 

qp=(0,2+0,72+0,3+1+0,5+0,008)kn/mq =2,72888 kn/mq

 

CARICHI ACCIDENTALI:

Per residenze da normativa 2 kn /mq

Fig.13

Nei calcoli il foglio exel tiene conto anche del peso della trave 

Fig.14

La trave di base 30 cm e di altezza 55 cm 

é verificata 

In questa esercitazione, l'obbiettivo è quello di comprendere come gli sbalzi siano parti della struttura che richiedono un'approfondimento maggiore, dato che rappresentano  dei punti critici.

Il solaio preso in eseme e qui riportato:

FIG.1

La trave in rosso, sarà la trave che andremo a dimensionare, poichè è quella a sbalzo con una maggior area d'influenza.

Area d'influenza= 15 mq 

Trave acciaio:

Il solaio preso in esame è cosi composto:

FIG.2

Pavimentazione: con piastrelle di 20cmx 20 cm hanno un pso di 0.31kn/mq

Massetto: calcestruzzo alleggerito 8 cm, il peso 16 kn/mc

Getto di completamento: area di 0.0953 mq con un peso specifico di 25kn/mc

Lamiera grecata: peso di 0.2 kn/mq

Travi: IPE area di  16,4 cmq e peso specifico di 78.5 kn/mc

Controsoffitto: 2 cm 0,26kn/mq

Dopo aver diviso i carichi in strutturali e carichi permanenti tenendo anche conto dei tramezzi e degli impianti come da normativa li vado ad inserire nella tabella excel, in cui aggiungo anche i carichi accidentali che per civili abitazioni si prende il valore di 2 kn/mq.

FIG.3

Mmax calcolato è analogo a quello calcolato nell'esercitazione precedente, ma in questa la luce è esattamente la metà.

Il momento di una mensola con un carico uniforme è max all'incastro e quivale a ql²/2, mentre quello di una trave appoggiata è max in mezzeria e quivale a ql²/8.

Dopo aver inserito i valori nella tabella trovo il Wx 1017,04 cmc e cerco un valore di Wx maggiore a quello trovato, scelgo 1160 cmc che corrispone a un IPE 400, si aggiunge poi il momento d'inerzia corrisponedente.

FIG.4

L'abbassamento Vmax è 0.972 cm 

il rapporto luce/ abbassamento è maggiore di 250 quindi è verificata.

La verifica a deformabilità è soddisfatta.

Solaio in calcestruzzo armato:

il solaio è cosi suddiviso:

Fig.5

 

 

Solaio in calcestruzzo armato:

il solaio è cosi composto

Pavimentazione: 2cm peso di 0,31 kn/mq

Massetto 8 cm peso 1,28 kn/MQ

Soletta 4 cm peso 1 kn/mq

Travetti 12cm x 20 cm=2 numero travetti x0,12x0,2x25kn/mc=1,2kn/mq

Pignatta ne ho 8 in un m peso 0,768 kn /mq

Controsoffitto 2cm 0,26kn/mq

Si suddividono i carichi strutturali, permanenti e accidentali, tenendo conto anche dei tramezzi e degli impianti.

Una volta analizzati i carichi si inseriscono nella tabella excel.

Fig.6

Come si può notare Mmax ha un valore molto vicino a quello dell'esecitazione precedente ma è necessario ricordare che in questo caso la luce è la metà.

Una volta stabilita la base di 20 cm, il copriferro, il modulo elstico e l'H ingegnerizzata, il programma ci calcolerà l'abbassameto Vmax, che corrispone a 0,74 cm.

Il rapporto luce/abbassamento è maggiore di 250, quindi la verifica a deformabilità è soddisfatta.

Proviamo ora a vedere se la verifica è soddisfatta utilizzando la stesssa trave, ma con la base di 30 cm.

FIG.7

In questo caso la verifica non è soddisfatta.

Riprendiamo ora la prima trave verificata quella con la base di 20 cm e vediamo se aumentando di 1 m la luce la trave resta comunque verificata.

FIG.8

Ma come si può notare anche in questo caso la verifica non è soddisfatta.

Solaio in legno:

Procediamo con la verifica di un solaio in legno cosi suddiviso:

FIG.9

Paviemntazione: 2cm peso 0,31kn/mq

Massetto: 8 cm peso 1,28 kn/mq

Tavolato: legno abete 4 cm peso 0,18 kn /mq

Travetto: legno lamellare abete 10 cm per 8 cm ne ho 2 in 1m peso 0,72 kn /mq

Controsofitto: 2 cm peso 0,26 kn /mq

Una volta eseguita l'analisi dei carichi si procede suddividendoli in carichi strutturali, permanenti e accidentali tenendo conto anche del contributo dei tramezzi e degli impianti.

Una volta calcolati tutti i carichi si inseriscono nella tabella excel.

FIG.10

 

Calcoliamo il peso della trave 

base x altezza =30 cm x 65=1950 cmq= 0,195 mq x 3 che è la luce= 0,585 mc (volume)

peso della trave 0,8775 kn/mq

Si inserisce poi il peso della trave nei carichi q.

L'abbassamento Vmax corrisponde a 0,86 cm.

Il rapporto luce/ abbassamento è maggiore di 250 quindi la verifica è soddisfatta.

 

 

 

 

 

Nella seconda esercitazione, è stato richiesto di dimensionare una trave portante, in 3 materiali diversi: Legno, Acciaio e Calcestruzzo armato.

Partendo da un pacchetto di solaio predefinito, e grazie all'ausilio del foglio exel per semplificare i calcoli, si è iniziato dal disegnare e definire un telaio.

Che riporto qui di seguito 

FIG.1

Per dimensionare una trave basta analizzare quella più sollecitata, cioè quella che porta la maggior porzione di solaio, nel mio caso è la trave evidenziata in rosso, la cui area di influenza è pari a 5mx6m=30mq.

TRAVE IN ACCIAIO:

il solaio che si è deciso di analizzare è cosi composto:

Pavimentazione: con piastrelle di 20cmx20cm con uno spessore di 2 cm hanno un peso di 0.31  kn/mq

Massetto: calcestruzzo alleggerito 8cm, il peso specifico varia dai 14-20 kn/mc, scelgo di utilizzare quello con il peso di 16 kn/mc.

Getto di completamento:area di 0.0935mq con un peso specifico di 25kn/mc

Lamiera grecata: peso di 0,2 kn/mq

Travi IPE 140: area di 16,4 cm² e peso specifico 78,5 kn/mc

Controsoffitto:2 cm peso  0,26 kn/mq

Per dimensionare una trave devo prima procedere con l'analisi dei carichi, fascendo una distinzione tra i carichi propri della struttura qs, il peso dei carichi permanenti qp e il peso dato dai carichi accidentali qa che sono legati principalmente all'utilizzo della struttura.

CARICHI STRUTTURALI  (qs)

travetti: 2 travetti IPE 140- 78,5X2X0.00164 mq=0,257 kn/mq

lamiera: 0.2 kn/mq

getto di completamento: 2,2 kn/mq

CARICHI PERMANENTI (qp)

pavimentazione: 0.31 kn/mq

massetto alleggerito: 1,28 kn/mq

controsoffitto: 0,26 kn/mq

tramezzi: 1 kn/mq (da normativa)

impianti: 0.5 kn/mq (da normativa)

Carichi accidentali (qa)

per civili abitazioni 2 kn/mq

una volta determinati i carichi andiamo ad inserire i valori trovati nel foglio exel, che terrà conto anche dei rispettivi coeff di sicurezza.

inoltre bisogna stabilire la classe di resistenza dell'acciaio, che in questo caso si è stabilita di 275 Mpa.

Si trova un Wx di 1017 (cmc) che in tabella corrisponde a un IPE 400 con un Wx di 1160 cmc.

Una volta dimensionata la trave è necessario ricalcolare il carico q tenendo conto questa volta anche del peso della trave appena dimensionata.

Dato che il Wx che tiene conto anche del peso della trave resta sempre inferiore al Wx della trave selezionata, tale profilo risulta verificato.

SOLAIO IN CALCESTRUZZO ARMATO:

Andiamo ora ad analizzare un solaio analogo in calcestruzzo armato.

Così suddiviso:

Pavimentazione:2 cm peso di 0,31 kn/mq

Massetto: 8 cm peso 1,28 kn/mq

Soletta:4 cm x 25 kn/mc=0,04x25= 1kn/mq

Travetti:12 cm x 20 cm = 2 il numero di travetti x 0,12x0,2x25kn/mc= 1,2 kn/mq

Pignatta:38 cm x20 cm x 25 kn/mc=

in 1m ho 4 pignatte del peso di 9,6x4 = 38,4 kg x2 = 76,8 kg/mq =0,768 kn/mq

Peso totale per 8 pignatte= 0,768 kn/mq

Controsoffitto: 2 cm 0,26 kn/mq

Carichi strutturali:(qs)

soletta:1 kn/mq

travetti:1,2 kn/mq

pignatte:0,768 kn/mq

Carichi permanenti:(qp)

pavimentazione:0,31 kn/mq

massetto:1,28 kn/mq

controsoffitto:0,26 kn/mq

tramezzi:1 kn/mq (da normativa)

impianti:0,5 kn/mq (da normativa )

carichi accidentali:(qa)

per il residenziale 2 kn/mq

Dopo aver concluso l'analisi dei carichi, e dopo aver stabilito le classi di resistenza  si procede inserendo i valori nel foglio exel, fissando un ipotetica base.

Da questa prima analisi, ipotiziamo una trave di h= 55 cm 

ma non si è ancora tenuto conto del peso della trave.

Si prosegue una nuova analisi dei carichi tenendo conto del peso propio della trave.

La nuova altezza calcolata è inferiore a quella ipotizzata, quindi la trave è verificata.

Proviamo ora a variare la base della trave questa volta di 30 cm e vediamo come varia l'altezza.

Ipotizziamo un altezza di 45 cm, ora andiamo a calcolare se questa altezza è sufficente per reggere anche il peso proprio della trave.

 

In questo caso la sezione non è verificata, poichè è necessario aumentare l'altezza a 50 cm.

SOLAIO IN LEGNO:

Pavimentazione:2 cm peso di 0,31kn/mq

Massetto: 8 cm peso 1,28 kn/mq

Tavolato: legno abete 4 cm     450kg/mc x 0,04 mc =18 kg/mq =0,18kn/mq

Travetto: legno lemellare abete  10 cm x 8 cm ne ho 2 in 1m 450kg/mc=720kg/mq=0,72kn/mq

Controsoffitto:2 cm peso 0,26 kn/mq

carichi strutturali:(qs)

travetto:0,72 kn/mq

tavolato:0,18 kn/mq

carichi permanenti:(qp)

pavimentazione: 0,31 kn/mq

massetto:1,28 kn/mq

controsoffitto:0,26 kn/mq

tramezzi: 1kn/mq da normativa

impianti:0,5 kn/mq da normativa

carichi accidentali: (qa)

per civili abitazioni 2 kn/mq

Riportiamo i valori calcolati nel foglio exel

Da questa prima analisi si ricava un primo predimensionamento che non tiene conto del peso della trave.

Da una prima scelta si stabilisce un altezza di primo tentativo della trave pari a 55 cm.

Andiamo ora a calcolare il peso della trave:

base x altezza= 30 cm x 55 cm= 1650 cmq=0,165 mq  x 6m che è la luce = 0,99 mc (volume)

0,99 x 4,5/6 = 0,7425 kn/mq

 

peso trave 0,7425x 1.3=0,965 kn/mq 

una volta calcolato il peso della trave, andiamo a inserire questo peso nel carico q.

La trave è verificata poichè anche tenendo conto del nuovo carico, l'altezza resta comunque inferiore dei 55 cm.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

La travatura reticolare è una struttura leggera che  consente di superare grandi luci.

Per la trave reticolare in 3d si è pensato di utilizzare una maglia regolare di 10 campate ripetute per 5 volte ottenendo cosi una reticolare di 50x25m.

Nonostante la grande luce di 50 m si è pensato per una prima ipotesi di vincolare la trave, solo nelle 4 estremità.

Fig.1

Per rendere più semplice il riconoscimento dei nodi sono stati numerati.

Fig.2

Il default di SAP da come nodi tra le aste degli incastri interni, per ottenere delle cerniere interne è necessario ad ogni asta assegnare momento nullo sia all'inizio che alla fine della medesima.

Fig.3

Si procede andando a definire e ad assegnare  il materiale e la  geometria della sezione.

In questo caso si è deciso di utilizzare l'acciaio e una geometria tubolare.

Fig.4

A questo punto si devono definire i carichi, si è scelto di posizionare le forze sui nodi superiori in modo da rendere il carico più equamente distribuito.

La forza è pari a 30 kn.

il carico che abbiamo impostato, non tiene conto del peso proprio, perchè in SAP genererebbe un momento diverso  da zero sulle aste.

Fig.5

Andiamo ora ad analizzare la deformata.

Fig.6

Il comportamento di questa trave reticolare, è assimilabile a una trave appoggiata, ovviamente in SAP le deformazioni sono portate all'eccesso, nella realtà non è soggetta a questa deformazione evidente.

Fig.7

Nella fase successiva andiamo a calcolare le reazioni vincolari.

Fig.8

Fig.9

Fig.10

Come ci aspettavamo dall'analisi degli sforzi,risulta nullo sia il taglio che il momento, infatti, è presente solo lo sfornzo normale.

Quello che risulta dai grafici, è che non tutte le aste sono sollecitate.

infine, grazie al programma exel, andiamo a vedere le aste più sollecitate, che in questo caso sono le aste n 259 e n 193.

Fig.11

Fig.12

Andiamo ora a vedere come cambia il comportamento di una struttura analoga,  con un numero maggiore  di vincoli.

Fig.13

 

Fig.14

Ripeto gli stessi passaggi, numerazione dei nodi,impongo le cerniere interne, lascio invarito sia la sezione che il materiale e ripotizzo una forza concentrata di 30 kn sui nodi superiori.

Si calcola poi la deformata.

Fig.15

Fig.16

Si passa in seguito ad analizzare le reazione vincolari, che ovviamente sono inferiori rispetto alla struttura vista in precedenza.

Fig.17

Fig.18

Anche qui come si pensava c'è presenza di sono sforzo normale.

Fig.19

Ora tramite il programma exel andiamo a vedere qual'è l'asta più soleccitata.

Fig.20

Come si può vedere le aste più soleccitate sono la n.386, la 388, 405  e la 407.

Ovviamente le sollecitazioni della trave maggiormente vincolata sono inferiori rispetto alla trave che ha solo i vincoli nelle 4 estremità.