CALCOLO DEL CENTRO DI RIGIDEZZA IN UN IMPALCATO CON TELAIO SHEAR-TYPE

Analizziamo il comportamento di un impalcato sollecitato da forze esterne orizzontali e il comportamento dei controventi nel rispondere a tali sollecitazioni.

I controventi vengono rappresentati come delle molle, in quanto rappresentano dei vincoli elastici, cioè in grado di rispondere alle forze esterne subendo una deformazione reversibile.

La capacità di queste molle di rispondere alle forze esterne sarà strettamente collegata alla loro rigidezza k e alla loro distanza dal centro delle rigidezze, unico punto in cui la risultante delle forze esterne applicate avrà momento pari a zero e dunque rotazione nulla.

Dunque una volta determinate le caratteristiche dimensionali e tipologiche dell’ impalcato e il materiale dei suoi elementi, attraverso un file excel si calcolerà il centro delle rigidezze.

Scelgliamo di analizzare il seguente impalcato in calcestruzzo:

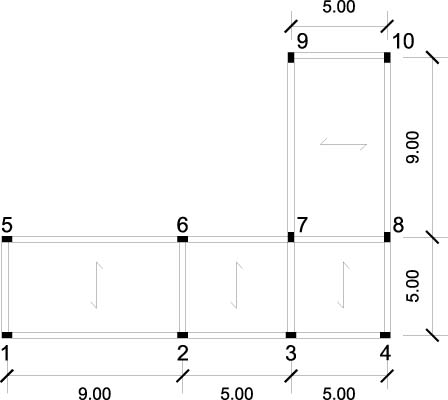fig.1

L’impalcato ha i seguenti controventi:

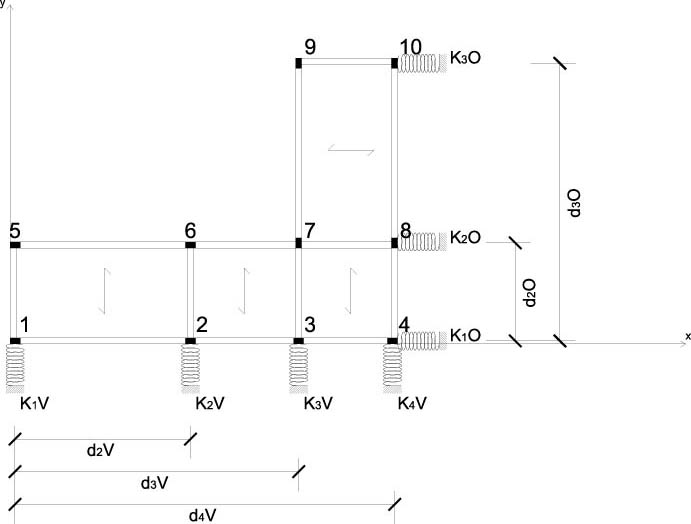fig.2

Dove:

d₂V= 9,00 mt

d₃V= 14,00 mt

d₄V= 19,00 mt

d₂O= 5,00 mt

d₃​O= 14,00 mt

Si tratta di un TELAIO SHEAR TYPE, infinitamente rigido, con rigidezza pari a 

K_t = 12 EI / h³

H PILASTRI: 4,00 m

PILASTRI IN CEMENTO ARMATO -> MODULO DI YOUNG : E= 21000 Nmm

SEZIONE PILASTRI:  30 x 50 cm

A seconda dell’ orditura del telaio avremo i pilastri orientati in 2 diversi modi e di conseguenza con diversi MOMENTI DI INERZIA.

 PILASTRI 7-8-9-10                PILASTRI 1-2-3-4-5-6

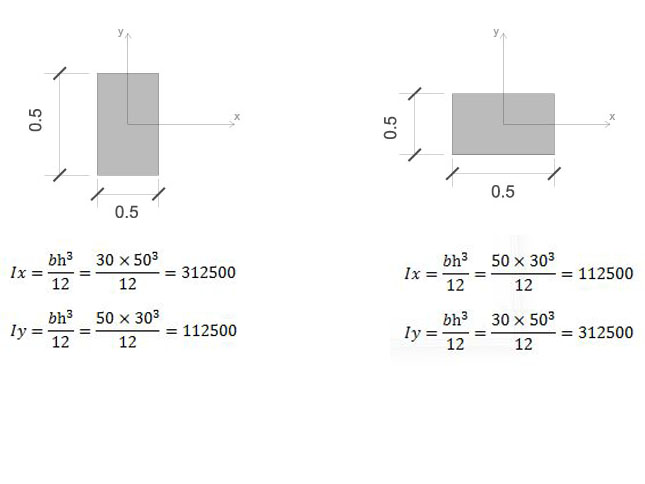fig.3

Prima di procedere con i calcoli su excel definiamo i telai, rispettivamente al piano cui appartengono. Si faccia riferimento alla fig.2 .

TELAIO VERTICALE_piano Y-Z                                         TELAIO ORIZZONTALE_piano X-Z     TELAIO 1 : PILASTRI 1-5                                                        TELAIO 5 : PILASTRI 1-2-3-4

TELAIO 2 : PILASTRI 2-6                                                        TELAIO 6 : PILASTRI 5-6-7-8

TELAIO 3 : PILASTRI 9-7-3                                                    TELAIO 7 : PILASTRI 9-10

TELAIO 4 : PILASTRI 10-8-4                                                  

STEP 1 Calcolo delle RIGIDEZZE TRASLANTI dei controventi dell’edificio.

Inseriamo nelle celle i dati relativi al nostro progetto. La rigidezza traslante dei controventi presi in analisi è data dalla somma delle rigidezze di ciascun pilastro.

STEP 2     Tabella sinottica dei controventi e delle loro distanze dell’origine

Ci permette di raccogliere dati sulle rigidezze traslanti prima ottenute e sulle loro distanze rispetto al centro 0, le quali dipendono dagli interassi e dalle luci tra i pilastri. 

STEP 3 Calcolo del CENTRO DELLE MASSE:

Al fine di determinare il baricentro della struttura, occore suddividere la stessa in aree:

Dove XG e Y_G sono le coordinate del punto G, centro di massa della struttura.

A1 tot = 95 mq

A2 tot = 45 mq

A tot   = 95 + 45 = 140 mq

STEP 4  Calcolo del CENTRO DI RIGIDEZZE e delle RIGIDEZZE GLOBALI:

Calcolando la rigidezza totale delle molle, quindi la capacità dei controventi di contrastare le forze agenti in direzione perpendicolare al telaio, troviamo la rigidezza totale orizzontale e la rigidezza totale verticale. Le sommiamo rispettivamente e facciamo la media ponderata.

Il centro delle rigidezze lo troviamo calcolando, per ogni molla, il prodotto della sua rigidezza per la sua distanza dal punto 0, origine degli assi. Sommiamo rispettivamente i prodotti ottenuti e li dividiamo per la rigidezza globale, dato ora noto.

Avremo  X_CDR e  Y_CDR, coordinate del centro di rigidezza globale.

La RIGIDEZZA TORSIONALE TOTALE K  è data dalla sommatoria dei prodotti delle rigidezze traslanti di ciascun telaio per la distanza al quadrato di ognuno di essi rispetto a C, centro delle rigidezze.

STEP 5 Analisi dei carichi sismici:

Consideriamo il carico del solaio in c.a. analizzato nella precedente esercitazione. Moltiplichiamo il suo valore per il coefficiente di contemporaneità, al fine di trovare i pesi sismici. I pesi sismici vengono moltiplicati inoltre per il coefficiente di intensità sismica. In questo modo potremmo risalire al valore della forza sismica agente sui telai. Occorre chiarire che tale valore rimane aleatorio, per questo motivo il coefficiente di intensità sismica si presenta elevato.

STEP 6 e 7: Ripartizione della forza sismica lungo X e Y

La forza sismica si ripartisce nelle due direzioni. Sappiamo che sio verificherà una rotazione in quanto il centro delle rigidezze e il centro delle masse non coincidono. Il momento torcente è dal tal calcolo Forzaxbraccio, dove il braccio è paari alla differenza tra le rispettive coordinate del centro delle masse e del centro delle rigidezze.

Troviamo la traslazione orizzontale Ux dividendo la forza simica per la resistenza globale orizzontale e la traslazione verticale Uy dividendo la forza sismica per la resistenza globale verticale.

Calcoliamo la rotazione dividendo il momento torcente (su X o su y) per la rigidezza torsionale totale Kφ.

Per capire quanta forza sismica si ripartisce su ciascuna molla, occorre moltiplicare la rigidezza della molla, per la somma tra lo spostamento (u) ed il prodotto tra rotazione φ e distanza dal centro delle rigidezze.

La reazione di ciascuna molla viene calcolata semplicemente moltiplicando la resistenza della molla cui si è interessati conoscere la reazione, per la traslazione che ad essa è perpendicolare (u oppure v).

Verifichiamo che l' analisi effettuata risponda correttamente se inserita in SAP. 

Vincoliamo la struttura al terreno meidante incastro:

Selezionando tutti i nodi dell' impalcato, applicando Diaphram, conferiamo una rigidezza tale al telaio, da avere solo traslazioni.

Assegnamo la sezione ai pilastri, considerando l' orientamento degli stessi come da progetto:

Con lo stesso metodo, assegnamo la sezione alle travi, impostando un momento d' inerzia tale che venga simulato il modello di telaio shear type, infinitamente rigido:

Applichiamo la Forza sul centro di rigidezza e analizziamo:

La struttura trasla, ma non ruota.