Esercitazione_4 - Centro delle rigidezze - Ripartizione della forza sismica

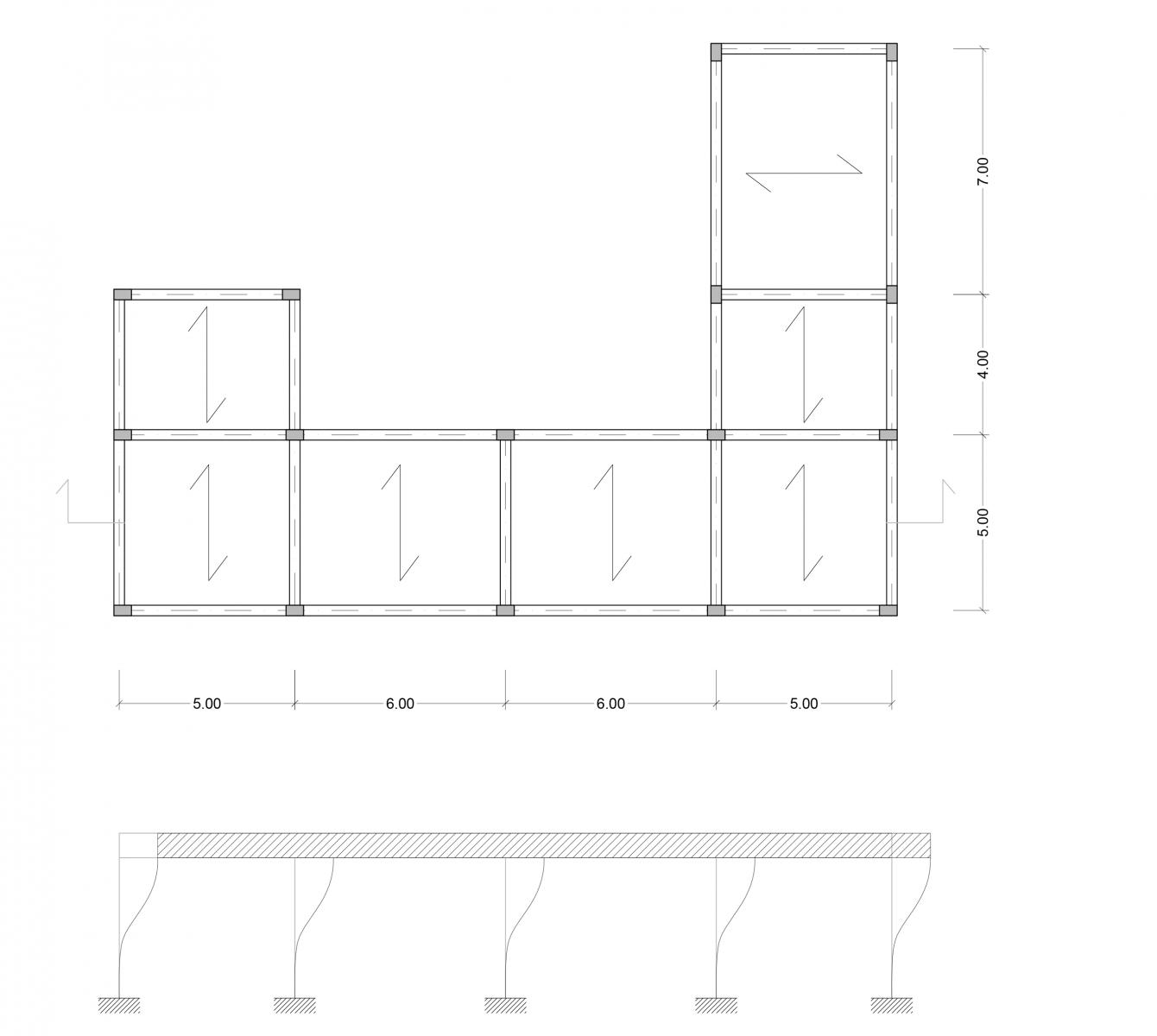
Analizziamo un impalcato in calcestruzzo armato composto da 10 telai piani, 5 lungo X e 5 lungo Y, e con pilastri di H=4m e sezione 30x40cm.

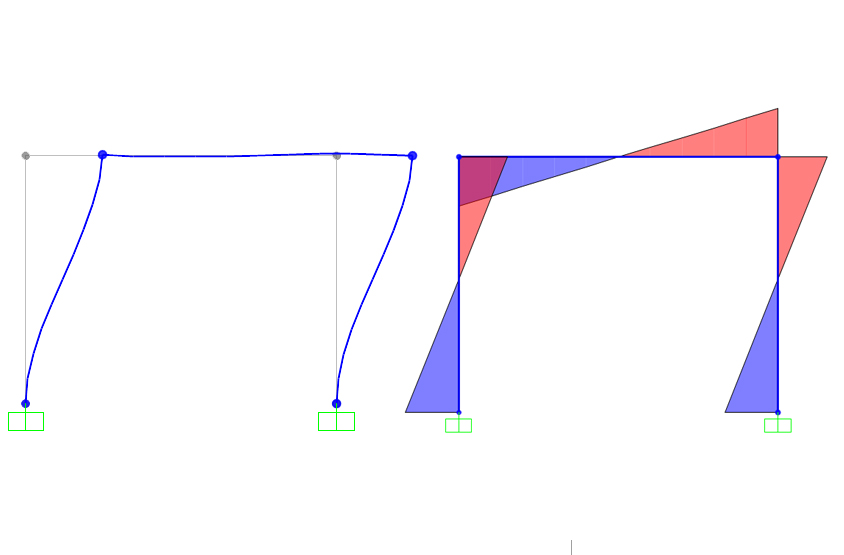
Sia il telaio del tipo SHEAR-TYPE:

• Le travi infinitamente rigide non si deformano assialmente;
• I pilastri sono soggetti a flessione.

Con K= 12EItot/h³

Prendiamo in considerazione un impalcato rigido nel suo piano, e siano i controventi dei vincoli cedevoli elasticamente e rappresentabili come molle, nel piano dell’impalcato. L’impalcato se sottoposto a forze orizzontali, come sisma e vento, può subire degli spostamenti. Bisogna quindi studiare come reagisce l’impalcato mediante l’azione dei controventi. 

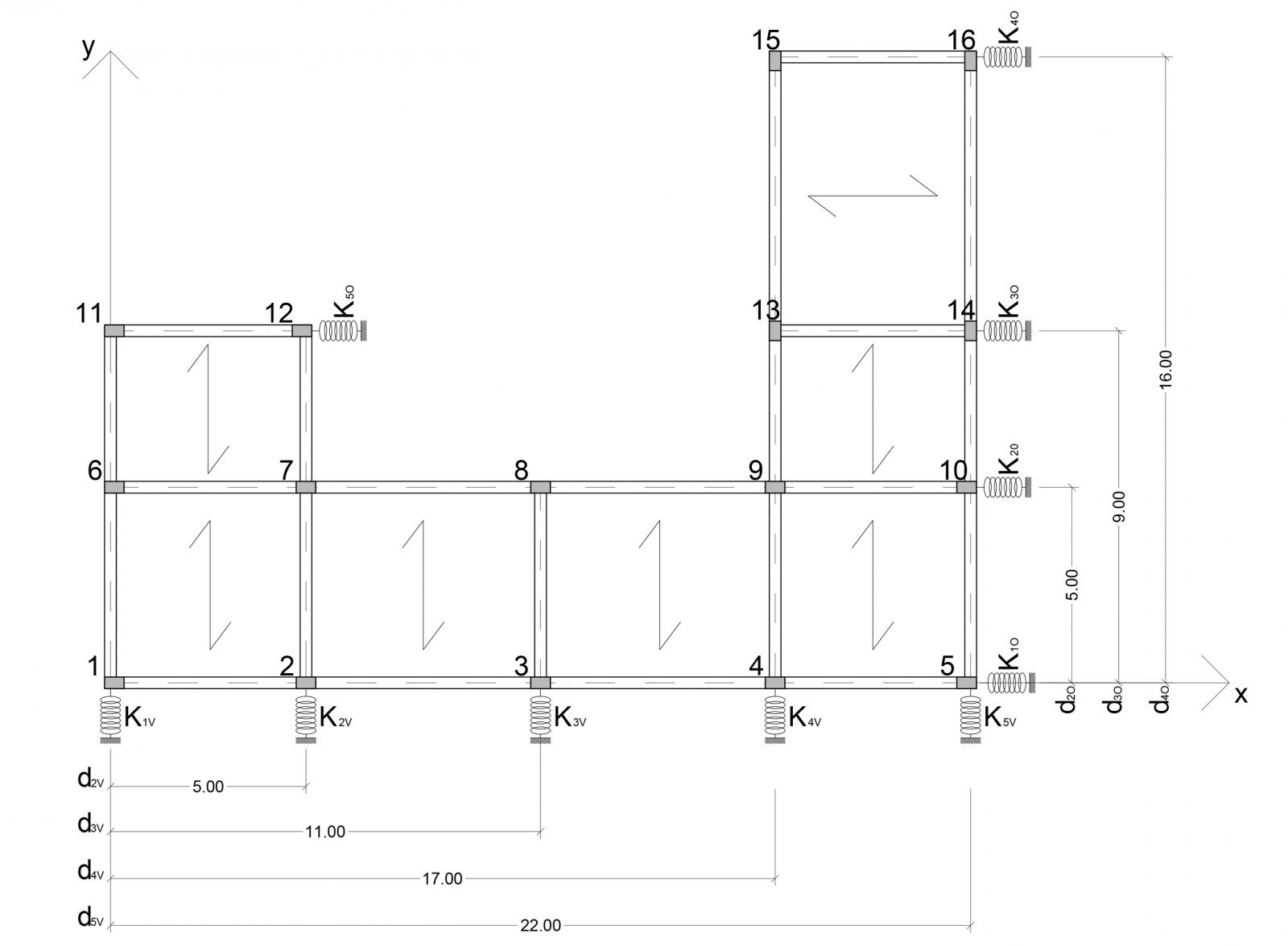
Siano:

Kv= rigidezza traslante dei controvento verticale

Ko=rigidezza traslante del controvento orizzontale

dv=distanza orizzontale del controvento dal punto O, origine degli assi

do=distanza verticale del controvento dal punto O

Il file excel, ci servirà per ripartire la forza orizzontale del sisma sui 10 controventi, dandone ad ognuno una parte, che è funzione della rigidezza del controvento e della sua distanza da un punto privilegiato (il centro delle rigidezze).

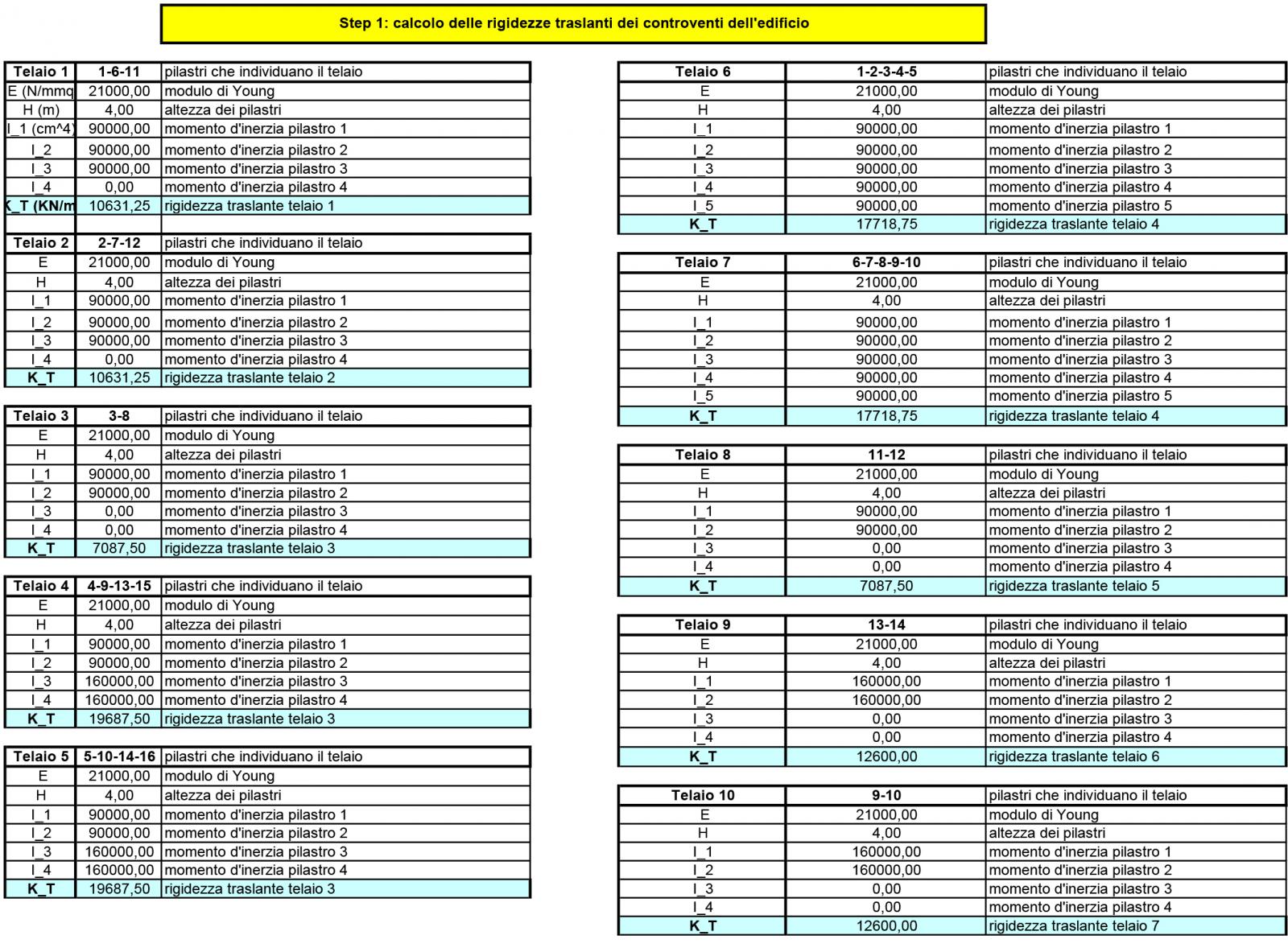
Step 1- Calcolo delle rigidezze traslanti dei controventi dell’edificio

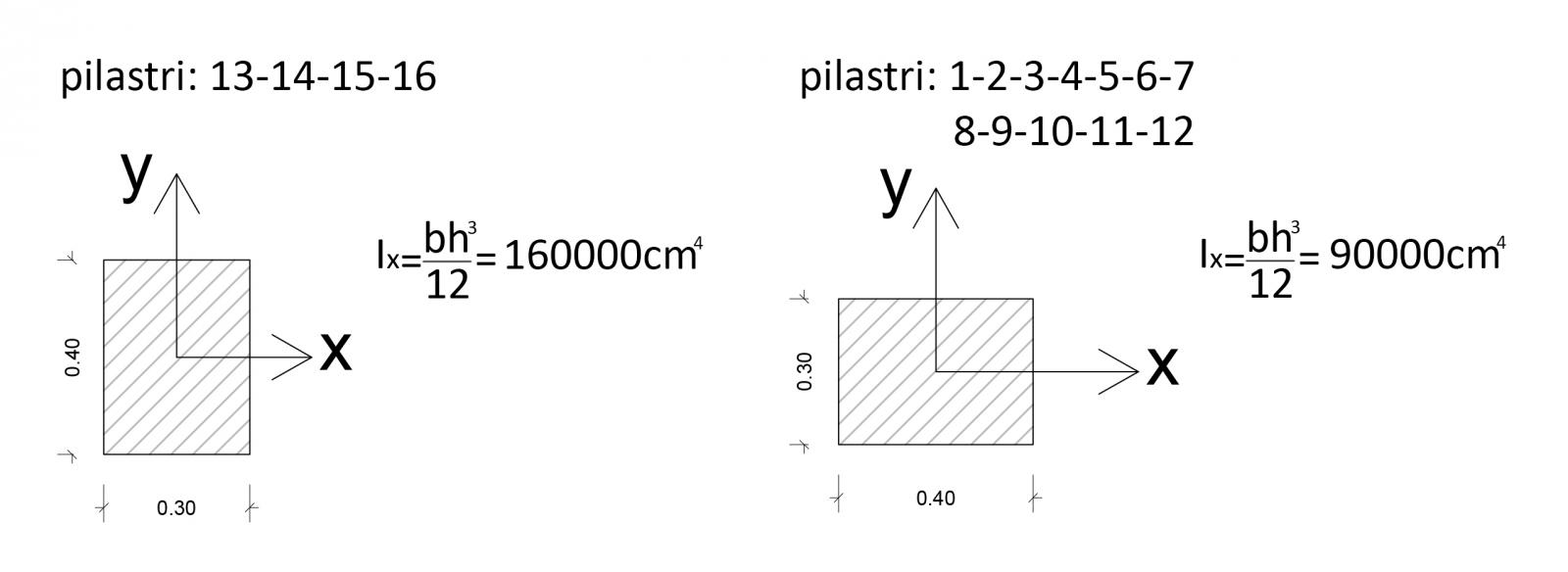
Prendendo in esame ogni singolo controvento, si determina la rigidezza K_T

Sia E=21000N/mmq e h=4m

K_T (KN/m)= 12EItot/h³

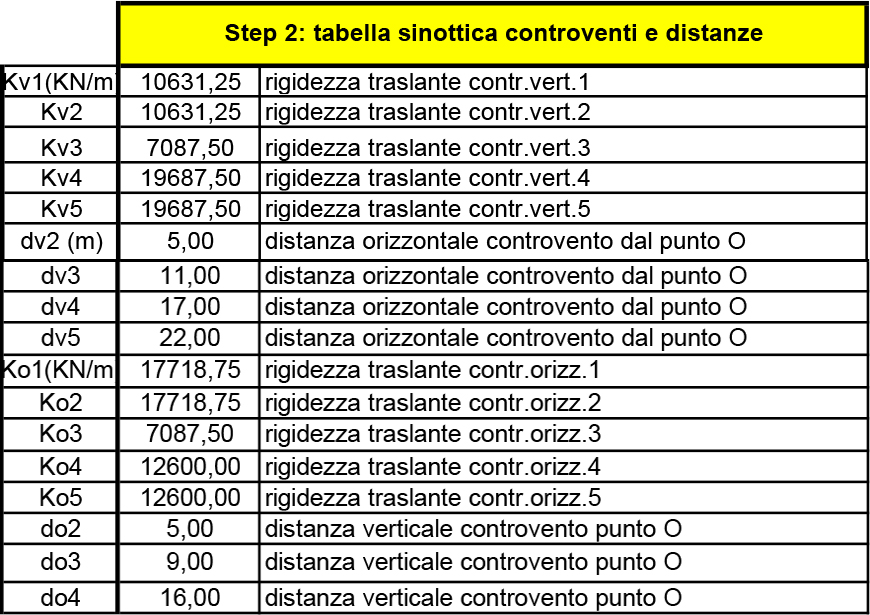
Step 2- Tabella sinottica controventi e distanze

La tabella 2 è una tabella riassuntiva che indica le rigidezze traslanti K_T dei controventi orizzontali e verticali precedentemente trovati e le distanze dei controventi rispetto all’origine del sistema di riferimento.

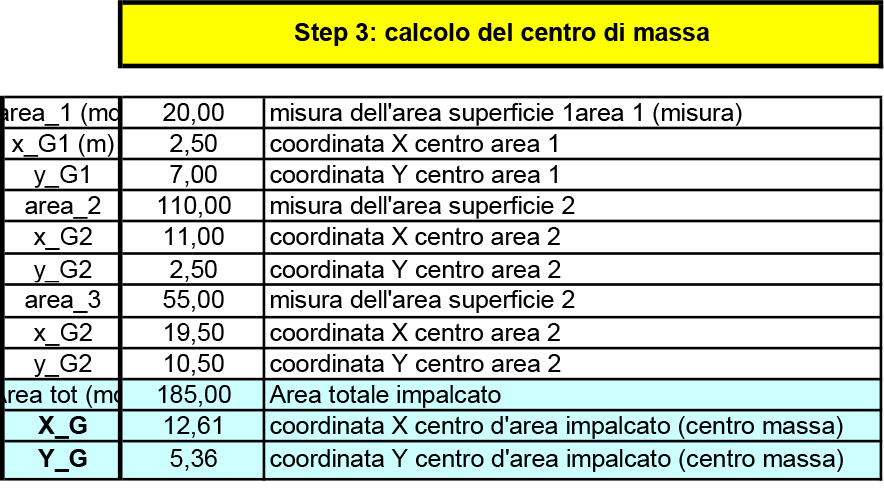
Step 3- Calcolo del centro di massa 

Per trovare il centro delle masse G è necessario dividere l’impalcato in 3 rettangoli semplici dai quali è possibile definire attraverso le diagonali i rispettivi centri delle masse. Infatti in una figura semplice, come un rettangolo, è possibile intuire facilmente il centro delle masse, ma avendo un impalcato complesso, il centro delle masse dipenderà dai centri delle masse dei rettangoli individuati e dalle rispettive aree.

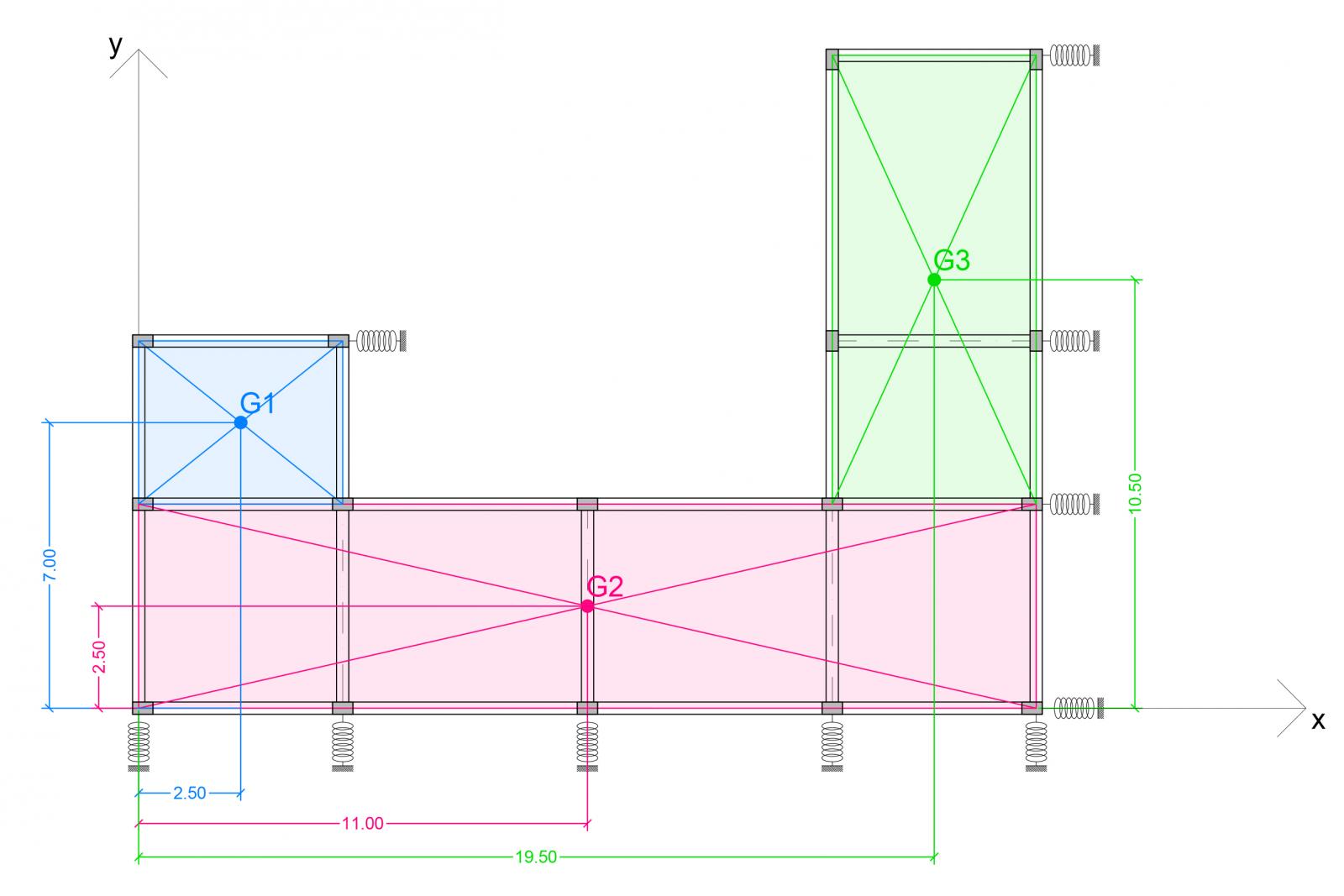
G1(2,5m;7m) - Area1= 20m²

G2(11m;2,5m) - Area2= 110m²

G3(19,5m;10,5m) - Area3= 55m²

Area tot= A1+A2+A3

Le coordinate di G saranno:

XG=∑Ai*XGi/Atot

YG=∑Ai*YGi/Atot

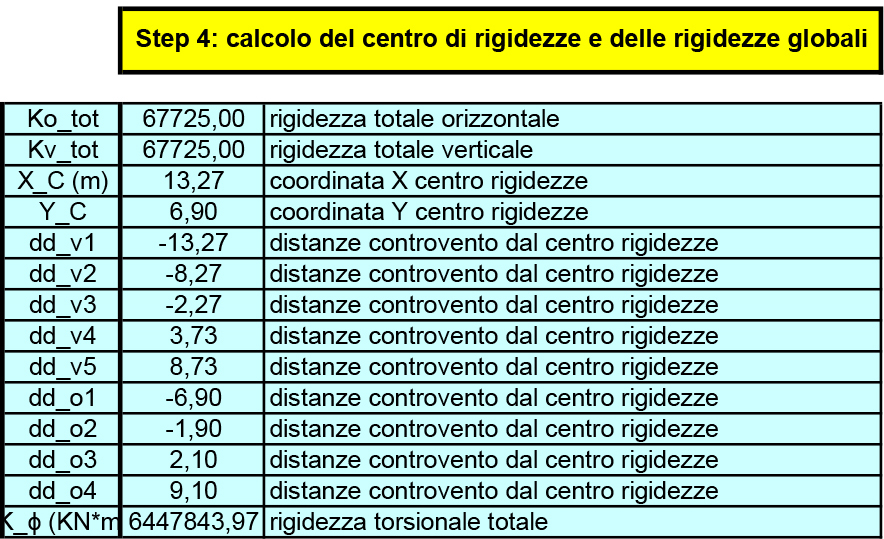
Step 4- Calcolo del centro delle rigidezze e delle rigidezze globali

Xc=∑Kvi*dvi/Kvtot

Yc=∑Koi*doi/Kvtot

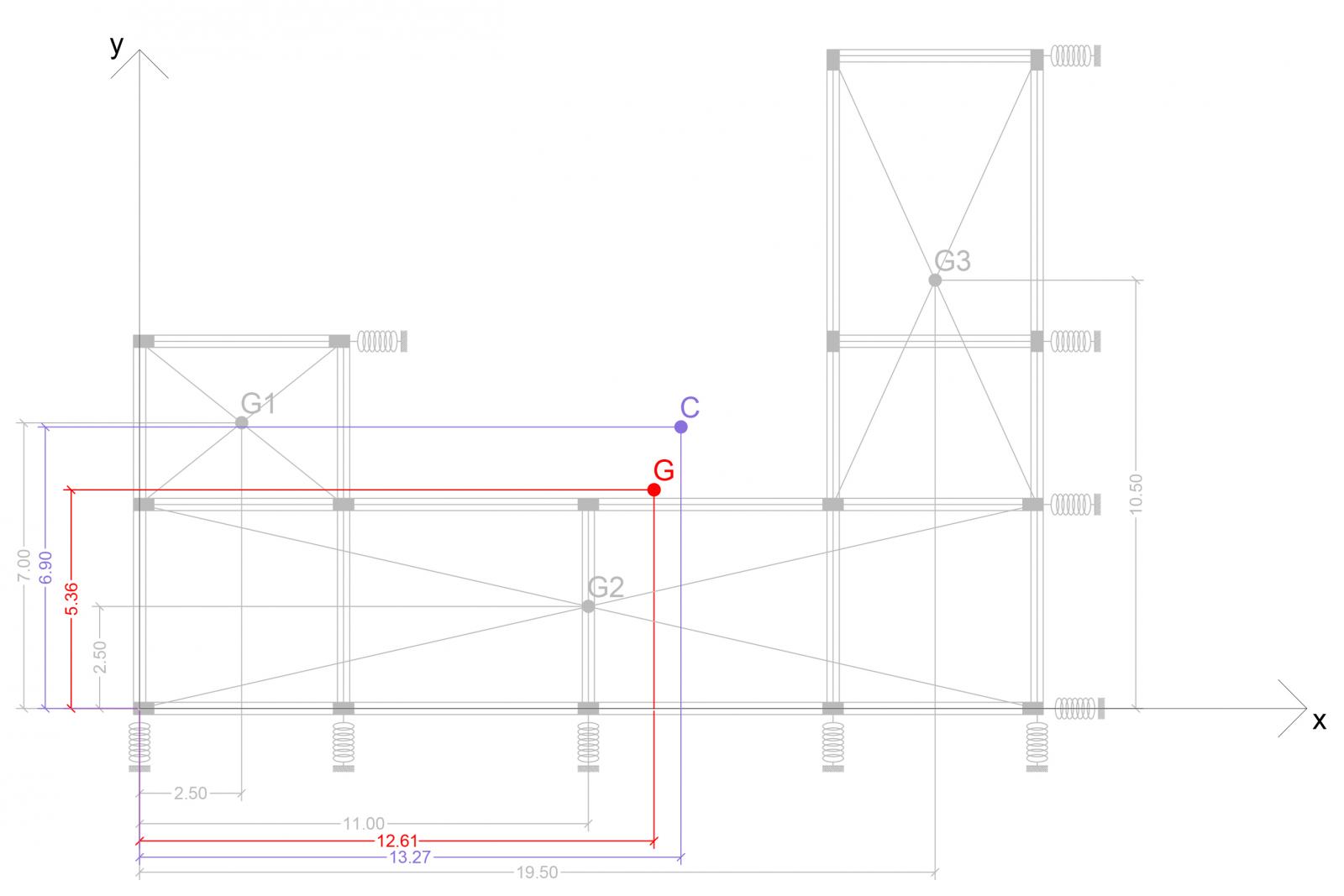
G(12,61m;5,36m)

C(13,27m;6,90m)

Dopo aver calcolato il centro di rigidezza, calcoliamo la rigidezza torsionale totale K_ϕ.

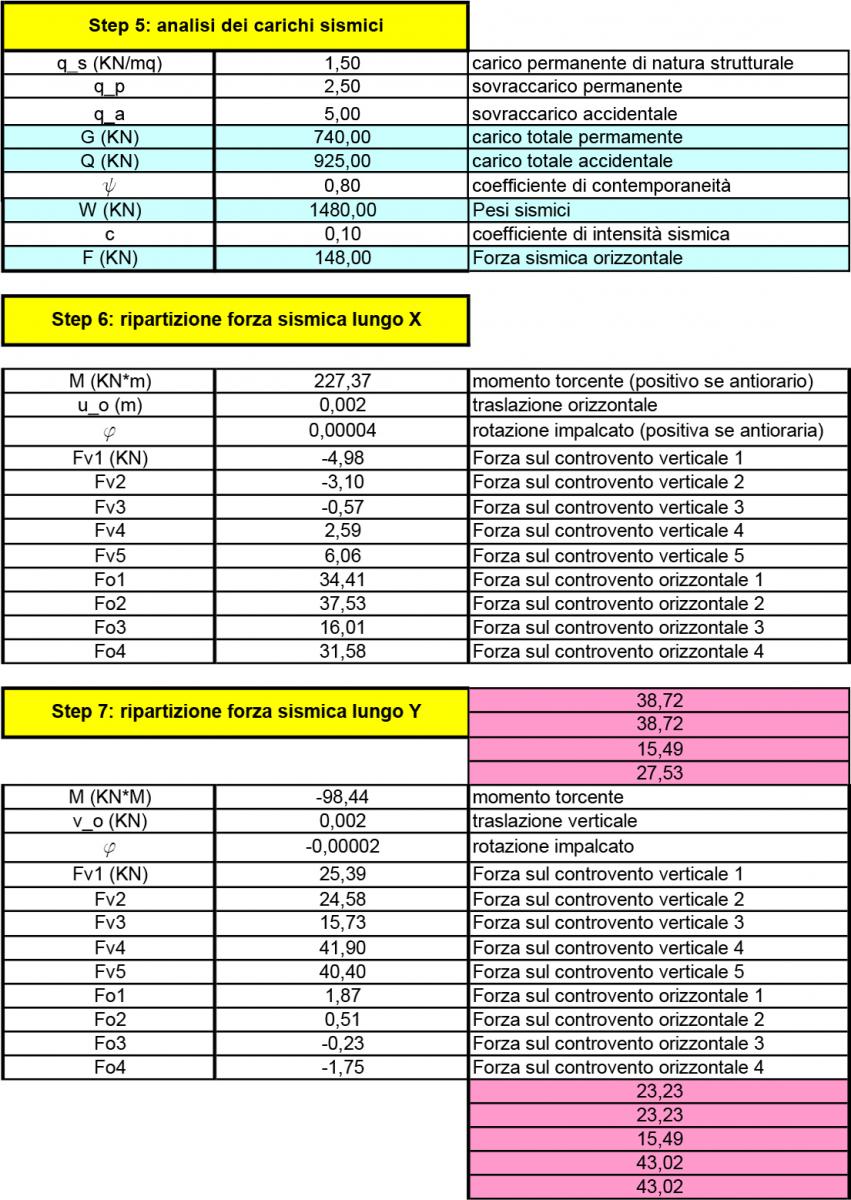
Step 5: analisi dei carichi sismici

Step 6: ripartizione della forza sismica lungo X

Step 7: ripartizione della forza sismica lungo Y

Infine calcoliamo l'analisi dei carichi sismici e la ripartizione della forza sismica lungo X e lungo Y.

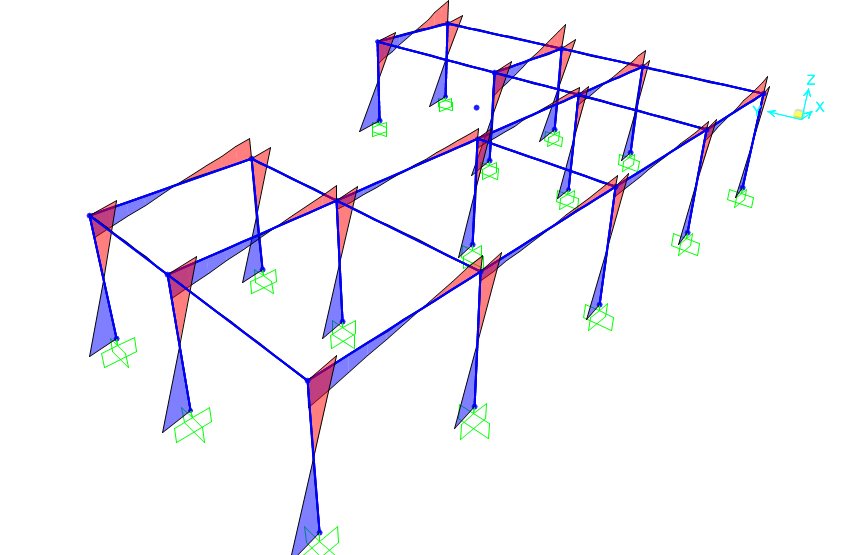
Verifichiamo ora su SAP che la struttura presa in esame, sottoposta  all’azione sismica nel centro delle rigidezze, subisca solo una traslazione.

Importiamo la struttura da Rhino su SAP, ed incastriamo i pilastri (Assign -> Joint -> Restraints)

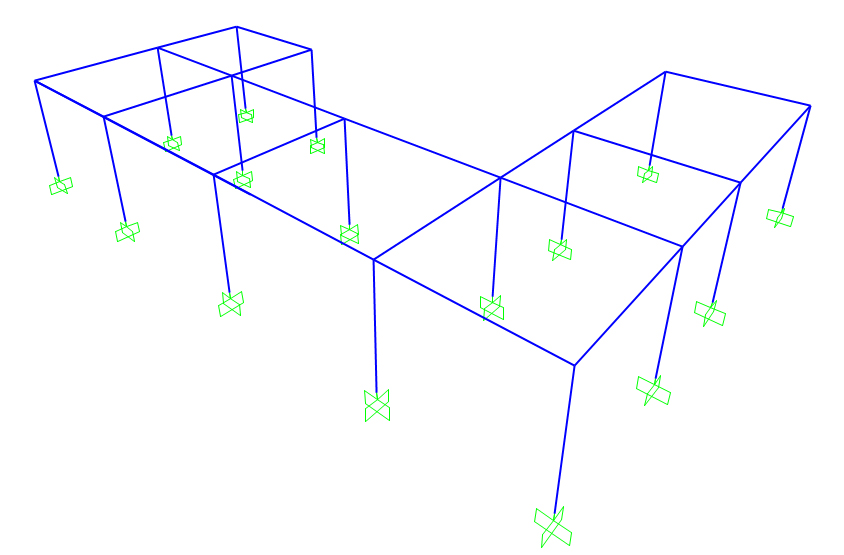
Dopo aver incastrato i pilastri, disegnamo il centro delle rigidezze.

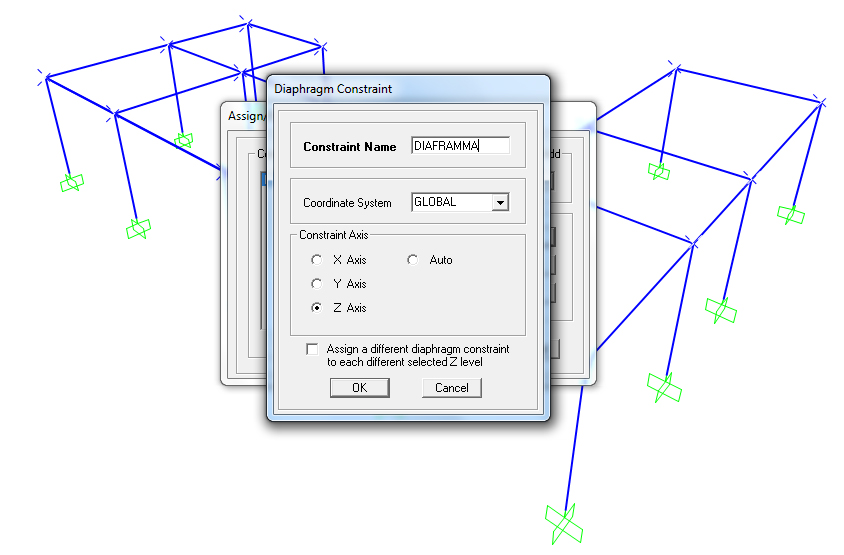
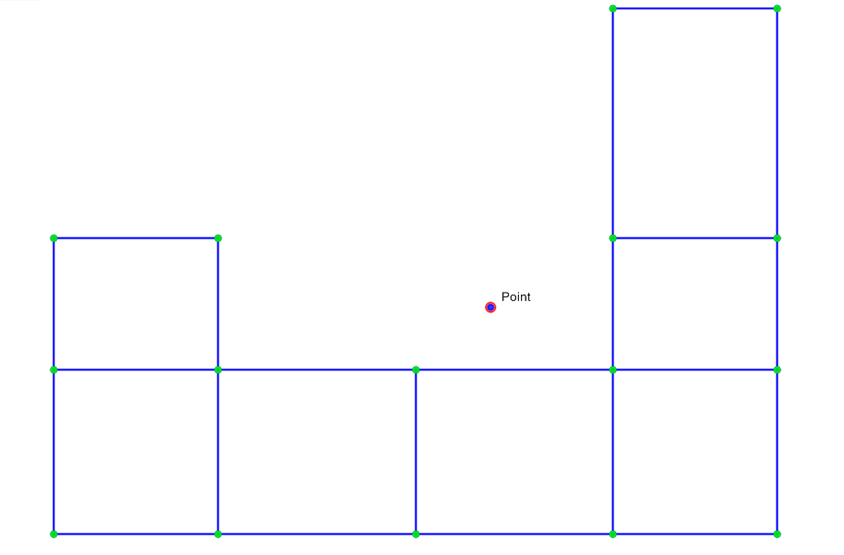Inseriamo quindi l'impalcato rigido, selezionando tutti i nodi tra travi e pilastri, compreso il centro delle rigidezze, assegnamo quindi il Diaphragm Constraint.

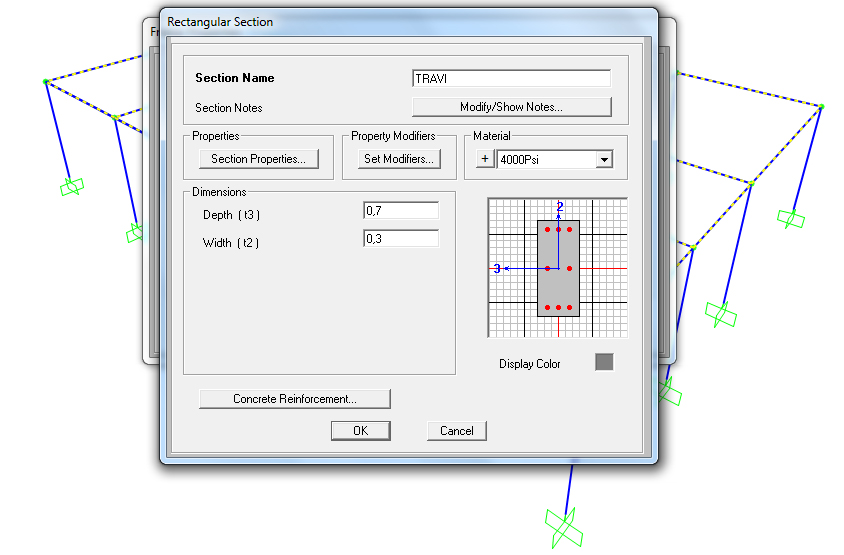
Assegnamo il materiale sia alle travi che ai pilastri, ricordandoci che stiamo prendendo in considerazione un telaio Shear Type quindi, aumentiamo con diversi zeri il Modulo di Elasticità (E) delle travi (infatti maggiore è il modulo di elasticità E, maggiore sarà la rigidezza K).

Applichiamo la forza sismica orizzontale nel centro delle rigidezze C ed avviamo l'analisi.

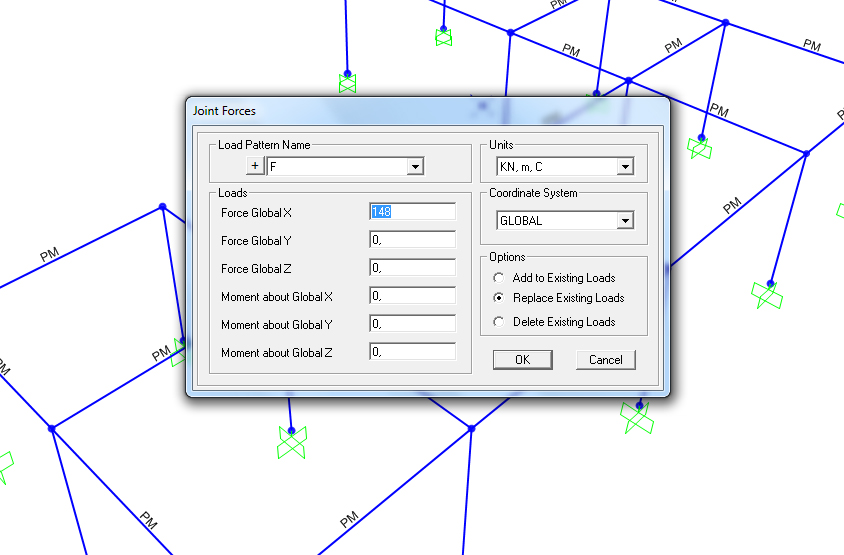
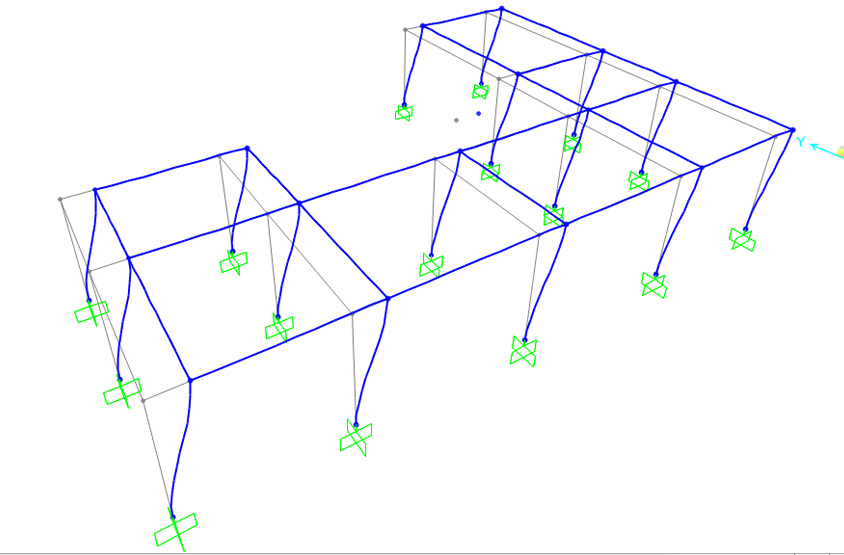
Si può notare come il centro delle rigidezze sia sottoposto a sola traslazione e non a rotazione.

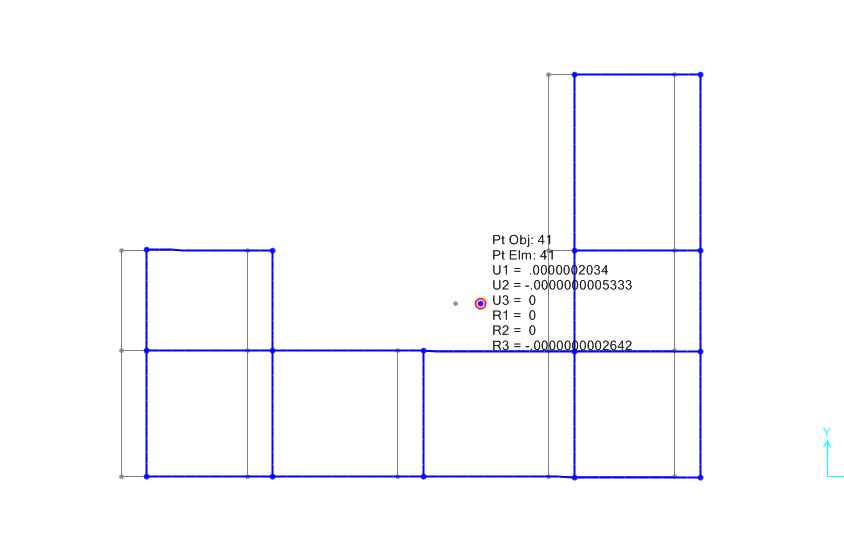
Inoltre dal diagramma dei momenti si può notare la somiglianza con il diagramma dei momenti del telaio Shear Type.