blog di Simona.Mazzei

L'ARCO

Prendiamo in considerazione 3 archi: arco a tutto sesto, arco ribassato e arco parabolico.

Mantenendo la stessa luce di 6 metri e lo stesso carico, facciamo variare la freccia.

1. Arco a tutto sesto: L=6m; f=3m
2. Arco ribassato: L=6m; f=1,5m
3. Arco parabolico: L=6m; f=6m

In questo modo dovremmo capire meglio i comportamenti dei 3 archi. Dai risultati si dovrebbe evincere come un arco più è ribassato, più è “arco”. Infatti, gli archi lavorano prevalentemente a sforzo normale ed è l’arco ribassato che prende i carichi e li trasforma maggiormente in sforzi normali.

Per studiare il comportamento dei 3 archi, utilizziamo SAP. Disegniamo su Autocad 3D o Rhinoceros l’arco ed importiamolo in formato dxf su SAP.

Dopo averlo importato, speziamo l’arco nella sezione di chiave e facciamo il rilascio dei momenti in chiave a applichiamo un carico distribuito pari a 10KN.

1. ARCO A TUTTO SESTO:

L'arco a tutto sesto o semicircolare è un tipo di arco contraddistinto da una volta a semicerchio. È la tipologia più semplice di arco e prevede che il centro verso il quale convergono i giunti si trovi sulla linea d'imposta, cioè su quella linea che unisce i punti dove finiscono i sostegni e inizia l'arco.

Si avrà questa deformata:

Le reazioni vincolari saranno:

Il grafico degli sforzi assiali:

Il grafico dei momenti:

2. ARCO RIBASSATO:

Un arco si dice ribassato quando il centro verso il quale tendono i giunti dei cunei si trova più in basso della linea d'imposta.

Si avrà questa deformata:

Le reazioni vincolari saranno:

Il grafico degli sforzi assiali:

Il grafico dei momenti:

3. L'ARCO PARABOLICO:

Si avrà questa deformata:

Le reazioni vincolari e il grafico degli sforzi assiali saranno:

CONCLUSIONE

Se osserviamo i grafici degli sforzi normali possiamo dedurre:

Arco a tutto sesto:

• All’imposta: N=30,38 KN
• In chiave: N=15 KN

Arco ribassato:

• All’imposta: N=42,15 KN
• In chiave: N=30 KN

Arco parabolico:

• All’imposta: N=7 KN
• In chiave: N=30,92 KN

Per quanto riguarda le reazioni vincolari si può facilmente vedere come la struttura più spingente sia l’arco ribassato, infatti la reazione vincolare orizzontale è 30KN, mentre quella dell’arco a tutto sesto è 15KN (la metà), e quella dell’arco parabolico è 7,50KN (un quarto). Praticamente l’arco ribassato ha una spinta doppia rispetto all’arco circolare ed ha sforzo normale maggiore.

30KN>15KN>7,50KN

Dai grafici dei momenti si può vedere come l’arco ribassato ha più sforzo normale e quindi meno momento flettente rispetto all’arco circolare.

Analizziamo un impalcato in calcestruzzo armato composto da 10 telai piani, 5 lungo X e 5 lungo Y, e con pilastri di H=4m e sezione 30x40cm.

Sia il telaio del tipo SHEAR-TYPE:

• Le travi infinitamente rigide non si deformano assialmente;
• I pilastri sono soggetti a flessione.

Con K= 12EItot/h³

Prendiamo in considerazione un impalcato rigido nel suo piano, e siano i controventi dei vincoli cedevoli elasticamente e rappresentabili come molle, nel piano dell’impalcato. L’impalcato se sottoposto a forze orizzontali, come sisma e vento, può subire degli spostamenti. Bisogna quindi studiare come reagisce l’impalcato mediante l’azione dei controventi. 

Siano:

Kv= rigidezza traslante dei controvento verticale

Ko=rigidezza traslante del controvento orizzontale

dv=distanza orizzontale del controvento dal punto O, origine degli assi

do=distanza verticale del controvento dal punto O

Il file excel, ci servirà per ripartire la forza orizzontale del sisma sui 10 controventi, dandone ad ognuno una parte, che è funzione della rigidezza del controvento e della sua distanza da un punto privilegiato (il centro delle rigidezze).

Step 1- Calcolo delle rigidezze traslanti dei controventi dell’edificio

Prendendo in esame ogni singolo controvento, si determina la rigidezza K_T

Sia E=21000N/mmq e h=4m

K_T (KN/m)= 12EItot/h³

Step 2- Tabella sinottica controventi e distanze

La tabella 2 è una tabella riassuntiva che indica le rigidezze traslanti K_T dei controventi orizzontali e verticali precedentemente trovati e le distanze dei controventi rispetto all’origine del sistema di riferimento.

Step 3- Calcolo del centro di massa 

Per trovare il centro delle masse G è necessario dividere l’impalcato in 3 rettangoli semplici dai quali è possibile definire attraverso le diagonali i rispettivi centri delle masse. Infatti in una figura semplice, come un rettangolo, è possibile intuire facilmente il centro delle masse, ma avendo un impalcato complesso, il centro delle masse dipenderà dai centri delle masse dei rettangoli individuati e dalle rispettive aree.

G1(2,5m;7m) - Area1= 20m²

G2(11m;2,5m) - Area2= 110m²

G3(19,5m;10,5m) - Area3= 55m²

Area tot= A1+A2+A3

Le coordinate di G saranno:

XG=∑Ai*XGi/Atot

YG=∑Ai*YGi/Atot

Step 4- Calcolo del centro delle rigidezze e delle rigidezze globali

Xc=∑Kvi*dvi/Kvtot

Yc=∑Koi*doi/Kvtot

G(12,61m;5,36m)

C(13,27m;6,90m)

Dopo aver calcolato il centro di rigidezza, calcoliamo la rigidezza torsionale totale K_ϕ.

Step 5: analisi dei carichi sismici

Step 6: ripartizione della forza sismica lungo X

Step 7: ripartizione della forza sismica lungo Y

Infine calcoliamo l'analisi dei carichi sismici e la ripartizione della forza sismica lungo X e lungo Y.

Verifichiamo ora su SAP che la struttura presa in esame, sottoposta  all’azione sismica nel centro delle rigidezze, subisca solo una traslazione.

Importiamo la struttura da Rhino su SAP, ed incastriamo i pilastri (Assign -> Joint -> Restraints)

Dopo aver incastrato i pilastri, disegnamo il centro delle rigidezze.

Inseriamo quindi l'impalcato rigido, selezionando tutti i nodi tra travi e pilastri, compreso il centro delle rigidezze, assegnamo quindi il Diaphragm Constraint.

Assegnamo il materiale sia alle travi che ai pilastri, ricordandoci che stiamo prendendo in considerazione un telaio Shear Type quindi, aumentiamo con diversi zeri il Modulo di Elasticità (E) delle travi (infatti maggiore è il modulo di elasticità E, maggiore sarà la rigidezza K).

Applichiamo la forza sismica orizzontale nel centro delle rigidezze C ed avviamo l'analisi.

Si può notare come il centro delle rigidezze sia sottoposto a sola traslazione e non a rotazione.

Inoltre dal diagramma dei momenti si può notare la somiglianza con il diagramma dei momenti del telaio Shear Type.

DIMENSIONAMENTO DI UNA TRAVE A SBALZO PER SOLAIO IN LEGNO, ACCIAIO E CLS

Dopo aver dimensionato una trave appoggiata, passiamo al dimensionamento di una trave a sbalzo.

Per il dimensionamento della trave a sbalzo utilizzeremo le tre tecnologie descritte nell’esercitazione precedente sia per quanto riguarda il legno, che per quanto riguarda l’acciaio e il calcestruzzo armato.

Il solaio preso in considerazione ha come interesse 4 metri e luce dello sbalzo 3 metri. Questi 2 valori andranno inseriti nella tabella excel rispettivamente nella casella interasse e nella casella luce.

SOLAIO IN LEGNO

Prendo in considerazione il solaio in legno composto da:

Parquet

Travetto

Pilastrino in mattoni

Tavella in cotto

Massetto

Tavolato

Travetto

Ricordo che l’analisi dei carichi dava come risultati:

Carichi strutturali qs= 0,317 Kn/ m²

Carichi permanenti qp= 4,85 KN/m²

Carichi accidentali qa= 2KN/m² (ambiente ad uso residenziale)

Il carico q che ne uscirà fuori sarà la somma dei carichi precedentemente detti moltiplicati per dei coefficienti di sicurezza: 1,3 per i carichi strutturali qs e i carichi permanenti qp e 1,5 per i carichi accidentali qa.

Trattandosi di una trave a sbalzo, la tabella tiene conto del momento di una mensola M=ql²/2 (nell’esercizio precedente M=ql²/8  perché si trattava di una trave appoggiata) nel nostro caso pari a M= 174,91kNm

Come fatto nell’esercitazione precedente scegliamo il tipo di legno, in questo caso un legno lamellare GL 24h con resistenza a flessione fm,k = 24MPa, si troverà quindi la tensione ammissibile (sigma ammissibile). Impostando la base b=30cm si troverà l'altezza H= 51,40cm. Ingegnerizziamo la sezione portando l’altezza della nostra trave a 55cm.

Inserendo una trave di altezza 55cm avremo uno spostamento Vmax= 1,18cm, e la verifica per cui l/Vmax>250 risulta soddisfatta in quanto 253,66>250. 

Adesso bisogna considerare il peso proprio della trave in modo tale da verificare se la trave appena dimensionata sia in grado di sopportare il peso proprio.

p= (0,30m x 0,55m x 1m)/m x 7KN/m³= 1,155 KN/m

Aggiungendo il peso proprio della trave la verifica l/Vmax>250 non risulta verificata. Possiamo quindi aumentare la sezione della trave, ricalcolare il peso proprio e reinserirlo nella tabella.

Prendiamo quindi una sezione di b=30cm e H=60cm

p= (0,30m x 0,60m x 1m)/m x 7KN/m³= 1,26 KN/m

Con una trave di altezza 60cm e base 30cm si riuscirà a superare lo sbalzo di 3m.

SOLAIO IN ACCIAIO

Prendo in considerazione il solaio in acciaio composto da:

pavimento

strato in cls alleggerito

getto in cls

lamiera grecata

trave secondaria IPE 180

Ricordo che l’analisi dei carichi dava come risultati:

Carichi strutturali qs= 2,64KN/m²

Carichi permanenti qp= 3,48 KN/m²

Carichi accidentali qa= 2KN/m² (ambiente ad uso residenziale)

Il carico q che ne uscirà fuori sarà la somma dei carichi precedentemente detti moltiplicati per dei coefficienti di sicurezza: 1,3 per i carichi strutturali qs e i carichi permanenti qp e 1,5 per i carichi accidentali qa.

Trattandosi di una trave a sbalzo, la tabella tiene conto del momento di una mensola M=ql²/2 nel nostro caso pari a M= 197,21kNm

Per dimensionare la trave è necessario confrontare il modulo di resistenza Wx dato dalla tabella Excel con i moduli di resistenza dati dal profilario.

Possiamo quindi prendere come trave una IPE 360 con Wx=904cm³ e Ix=16270cm^4.

Inseriamo il peso proprio p della trave nella tabella Excel.

p= (0.00727m² x 1m)/m x 78,50 KN/m³=0,57 KN/m

Il modulo di resistenza che ne risulta è di Wx= 904,41cm³ > 904cm³ dell’IPE 360. Devo quindi cambiare l’IPE scelta precedentemente.

Considero quindi un’ IPE 400 con peso proprio:

p= (0.00845m² x 1m)/m x 78,50 KN/m³=0,67 KN/m

Il modulo di resistenza che ne risulta è di Wx= 960,07 cm³ < 1160cm³ dell’IPE 400. Inoltre l/Vmax>250 in quanto 367,99 > 250.

Con una trave IPE 400 si riuscirà a superare lo sbalzo di 3m.

SOLAIO IN CLS

Prendo in considerazione il solaio in cls composto da:

pavimento

allettamento

massetto

cls armato

pignatte

intonaco

Ricordo che l’analisi dei carichi dava come risultati:

Carichi strutturali qs= 3,91 KN/m²

Carichi permanenti qp= 3,63 KN/m²

Carichi accidentali qa= 2KN/m² (ambiente ad uso residenziale)

Il carico q che ne uscirà fuori sarà la somma dei carichi precedentemente detti moltiplicati per dei coefficienti di sicurezza: 1,3 per i carichi strutturali qs e i carichi permanenti qp e 1,5 per i carichi accidentali qa.

Trattandosi di una trave a sbalzo, la tabella tiene conto del momento di una mensola M=ql²/2 nel nostro caso pari a M= 230,43KNm

Per le armature scelgo una resistenza caratteristica fyk=450 MPa mentre per il cls prendo C 40/50 con resistenza caratteristica a compressione Rck=50Mpa. Quindi con una base b=30cm, avrò un'altezza H=40,29cm. Ingegnerizziamo quindi la sezione portandola ad un'altezza H=45cm.

Sia p il carico proprio della trave.

p = (0,30m x 0,45m x 1m)/m x 25KN/m³ = 3,375 Kn/m

Avremo  quindi una sezione di altezza H=41,77cm < 45cm. Inoltre l/Vmax>250. 

Con una trave di altezza 45cm e base 30cm si riuscirà a superare lo sbalzo di 3m.

Dimensionamento della trave più sollecitata del solaio in figura. L'operazione verrà eseguita per il dimensionamento di una trave in cls armato, in acciaio e in legno.

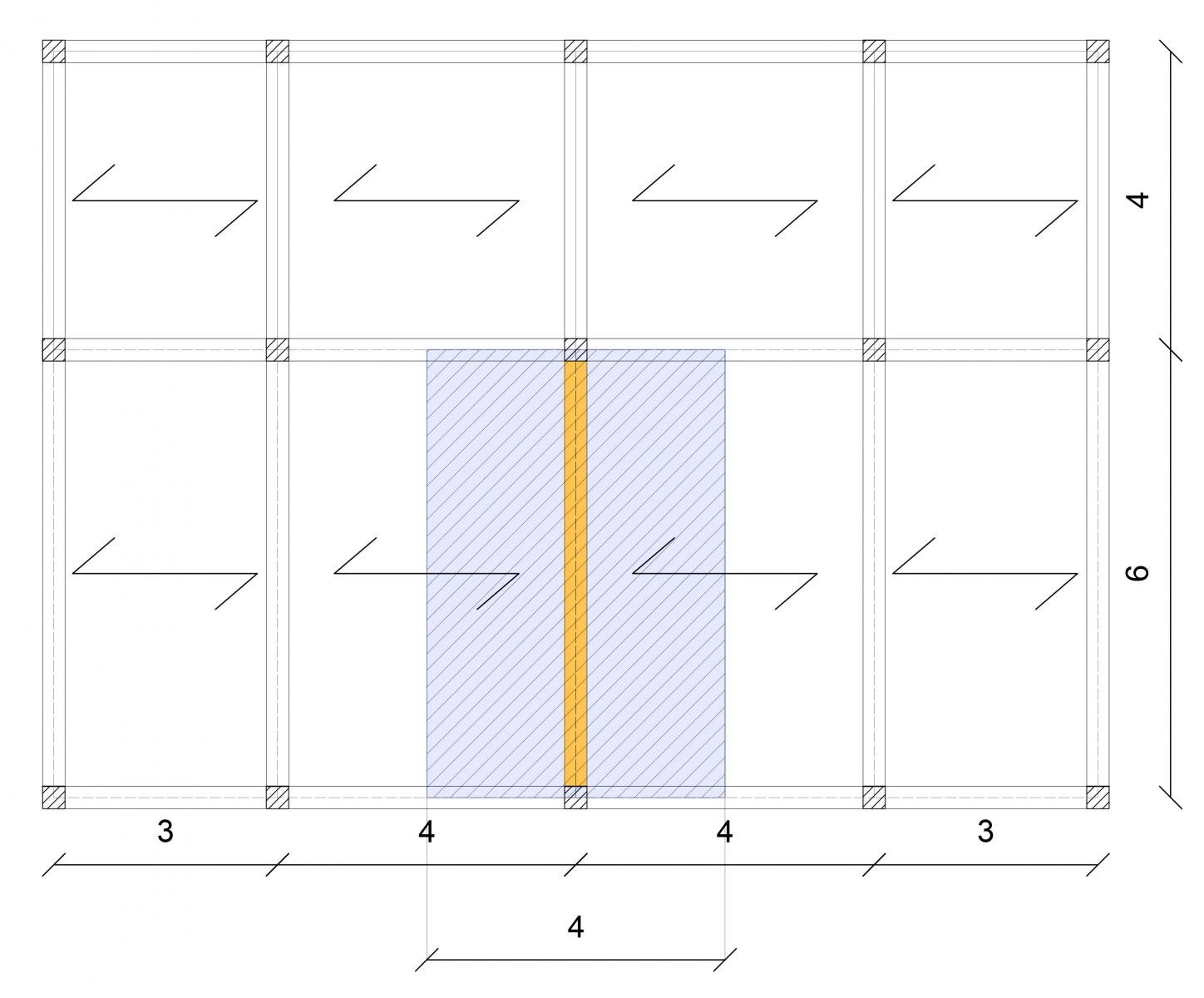
Prendo in considerazione il solaio in figura, la trave più sollecitata è quella in evidenza poichè l'area di influenza è maggiore rispetto alle altre ed è pari a 4m x 6m = 24m² 

Per il calcolo ci aiuteremo con un foglio Excel preimpostato.

SOLAIO IN CALCESTRUZZO

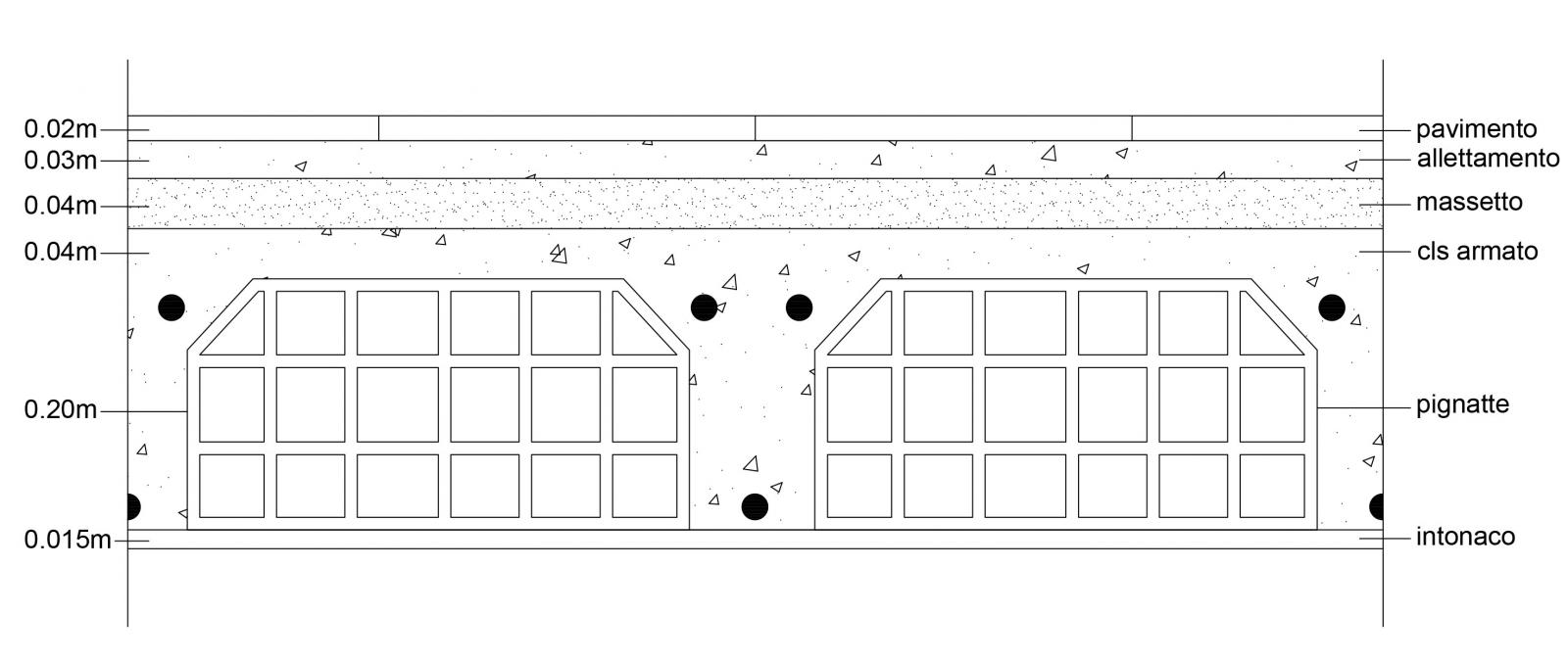
Il primo passo è fare l'analisi dei carichi strutturali qs, i carichi permanenti qp e i carichi accidentali qa.

Analisi dei carichi strutturali qs

Pignatte

(0,20m x 0,40m x 1m)/m² x 11KN/m³ x 2 = 1,76KN/m²

Calcestruzzo armato

(0,086m³/m²) x 25KN/m³ = 2,15KN/m²

TOTALE= 1,76KN/m² + 2,15KN/m² = 3,91 Kn/m²

Analisi dei carichi permanenti qp

Intonaco

(0,015m x 1m x 1m)/m² x 18 KN/m³ = 0,27 KN/m²

Massetto

(0,04m x 1m x 1m)/m² x 18KN/m³ = 0,72 KN/m²

Allettamento

(0,03m x 1m x 1m)/m² x 20 KN/m³ = 0,6 KN/m²

Pavimento (granito)

(0,02m x 1m x 1m)/m² x 27Kn/m³ = 0,54 KN/m²

Totale = 0,27 KN/m² + 0,72 KN/m² + 0,6 KN/m² + 0,54 KN/m²

Si aggiungono ai carichi permanenti, i carichi dati dalla normativa, dei tramezzi (1KN/m²) e degli impianti (0,5KN/m²)

TOTALE= 2,13 KN/m² + 1KN/m² + 0,5KN/m² = 3,63 KN/m²

Analisi dei carichi accidentali qa

Ambiente ad uso residenziale (Normativa)

TOTALE = 2KN/m²

Dopo aver fatto i calcoli inseriamo nella tabella i carichi strutturali qs, i carichi permanenti qp e i carichi accidentali qa. La tabella moltiplicherà tali valori per un coefficiente di sicurezza di 1,3 per i qs e i qp e 1,5 per i qa. La trave presa in considerazione è una trave appoggiata quindi il momento è pari a M= ql²/8. Per le armature scelgo una resistenza caratteristica fyk=450 MPa mentre per il cls prendo C 40/50 con resistenza caratteristica a compressione Rck=50Mpa. Quindi con una base b=30cm, avrò un'altezza H=40,50cm. Ingegnerizziamo quindi la sezione portandola ad un'altezza H=45cm.

In questo calcolo non abbiamo tenuto conto del peso proprio della trave. Dobbiamo quindi inserire il peso proprio della trave nella tabella excel, per verificare che la trave che abbiamo dimensionato con sezione di 45cmx30cm vada bene.

Sia p il carico proprio della trave.

p = (0,30m x 0,45m x 1m)/m x 25KN/m³ = 3,375 Kn/m

Il carico dovrà essere inserito nella casella q della tabella excell moltiplicato per il fattore di sicurezza 1,3. Se la nuova H sarà minore di 45cm allora il dimensionamento è stato fatto correttamente.

La sezione precedentemente dimensionata risulta verificata.

SOLAIO IN ACCIAIO

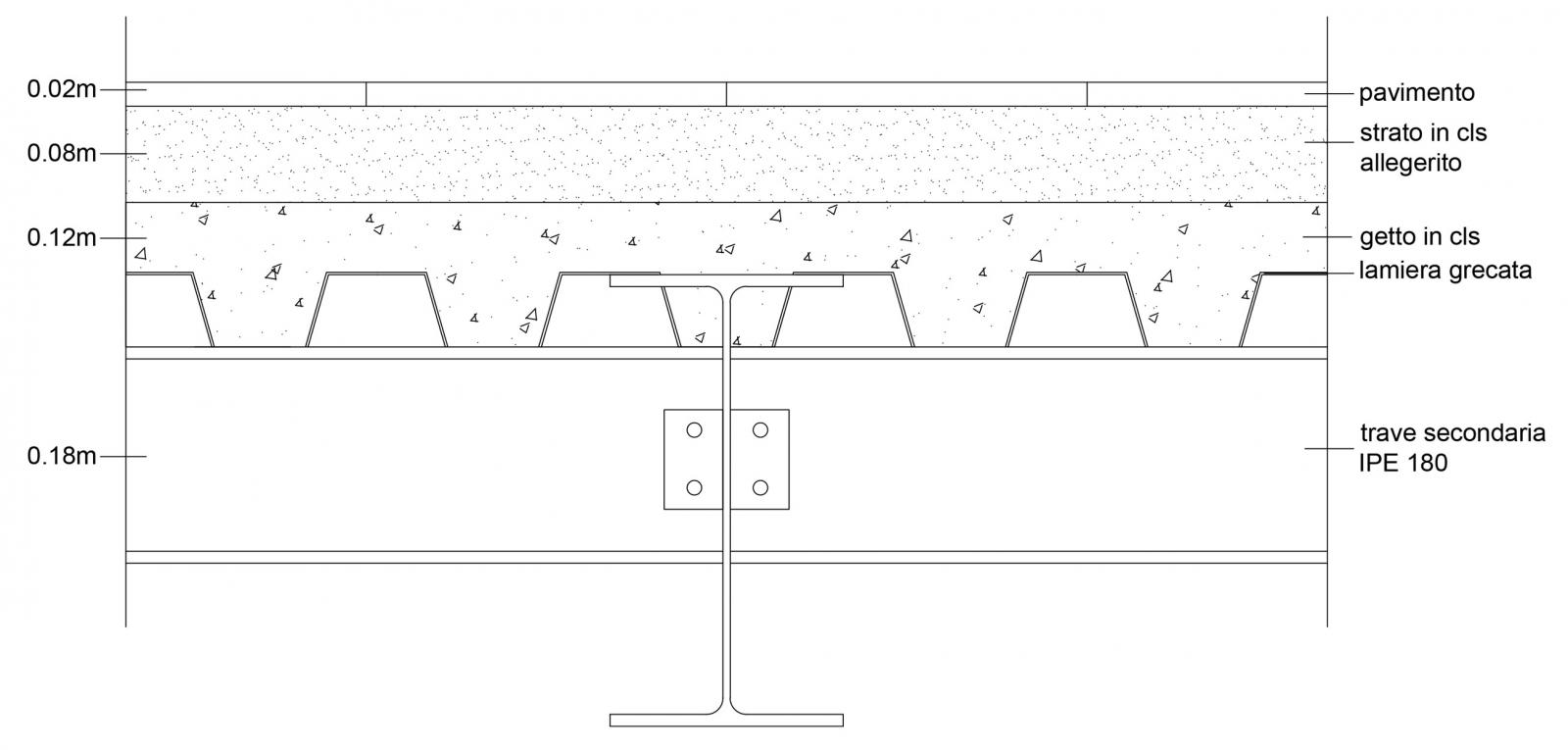
Analisi dei carichi strutturali qs

Travi secondarie (IPE 180)

(0,00239m² x 1m)/m² x 78,50 KN/m³ x 2 = 0,38KN/m²

Lamiera grecata

0,10 KN/m²

Getto in cls

(0,09m² x 1m)/m² x 24KN/m² = 2,16KN/m²

TOTALE= 0,38KN/m² + 0,10 KN/m² + 2,16 KN/m² = 2,64KN/m²

Analisi dei carichi permanenti qp

Strato in cls alleggerito

(0,08m x 1m x 1m)/m² x 18KN/m³ = 1,44 KN/m²

Pavimento (granito)

(0,02m x 1m x 1m)/m² x 27KN/m³ = 0,54 KN/m²

Si aggiungono ai carichi permanenti, i carichi dati dalla normativa, dei tramezzi (1KN/m²) e degli impianti (0,5KN/m²)

TOTALE= 1,44 KN/m² + 0,54KN/m² + 1KN/m² + 0,5KN/m² = 3,48 KN/m²

Analisi dei carichi accidentali qa

Ambiente ad uso residenziale (Normativa)

TOTALE = 2KN/m²

Inseriamo i carichi nella tabella excel, come fatto precedentemente.

Per dimensionare la trave è necessario confrontare il modulo di resistenza Wx dato dalla tabella Excel con i moduli di resistenza dati dal profilario.

Possiamo quindi prendere come trave una IPE 400 con Wx=1160cm³.

Inseriamo il peso proprio p della trave nella tabella Excel.

p= (0.00845m² x 1m)/m x 78,50 KN/m³=0,67 KN/m

La sezione precedentemente dimensionata risulta verificata.

SOLAIO IN LEGNO

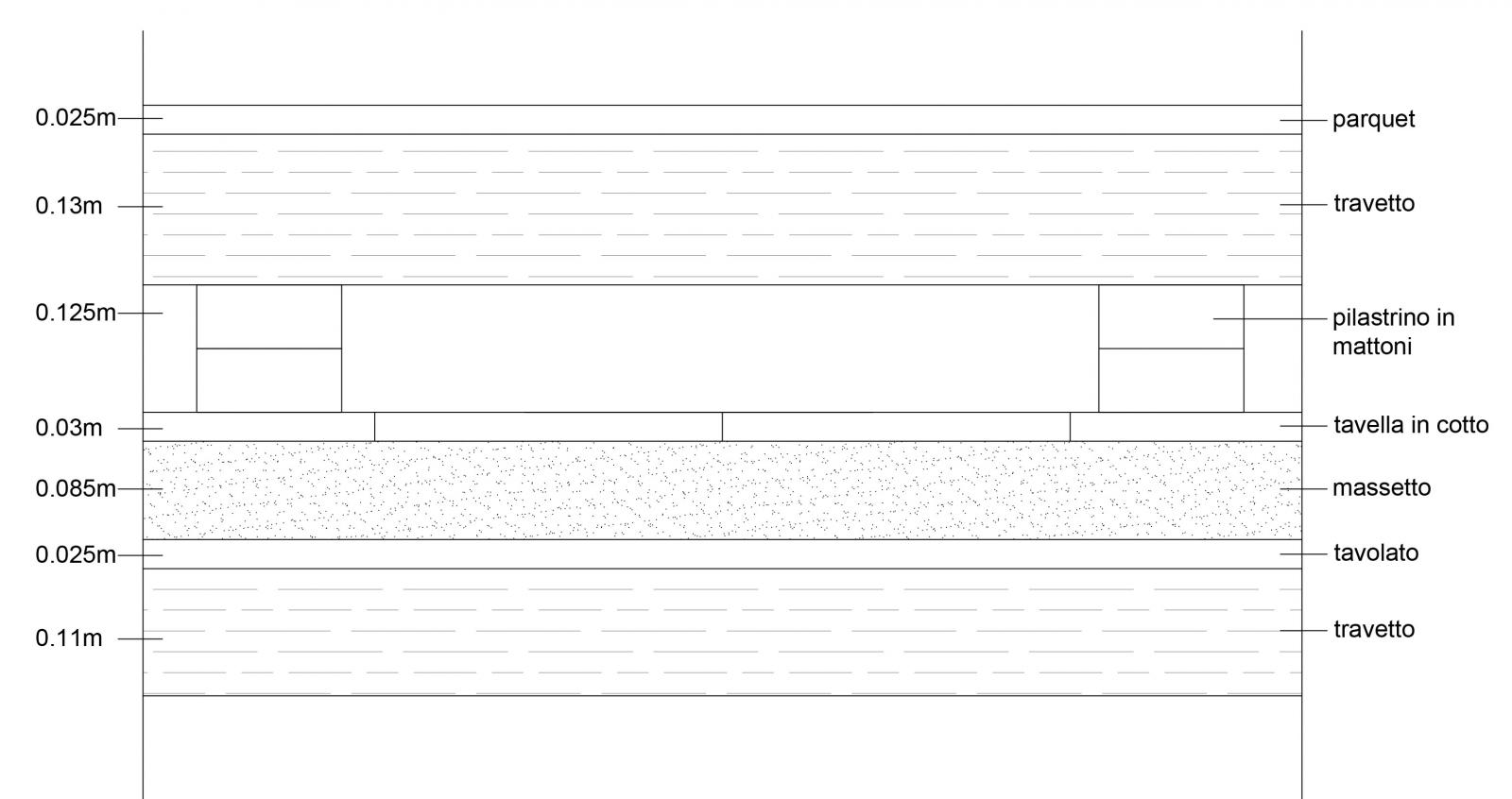
Analisi dei carichi strutturali qs

Travetto

(0,09m x 0,11m x 1m)/m² x 8KN/m³ x 4 = 0,317 Kn/ m²

TOTALE= 0,317 Kn/ m²

Analisi dei carichi permanenti qp

Parquet-Rovere

(0,025m x 1m x 1m)/m² x 7,2 KN/m³ = 0,18 KN/m²

Travetto Parquet

(0,13m x 0,08m x 1m)/m² x 6 KN/m³ x 3= 0,1872 KN/m²

Pilastrini in mattoni

(0,125m x 0,25m x 1m)/m² x 18KN/m³ x 12= 0,5625 KN/m²

Tavella in cotto

(0,03m x 1m x 1m)/m² x 18KN/m³= 0,54 KN/m²

Massetto

(0,085m x 1m x 1m)/m² x 20KN/m³ = 1,7 KN/m²

Tavolato in pioppo

(0,025m x 1m x 1m)/m² x 7KN/m³ = 0,175 KN/m²

Si aggiungono ai carichi permanenti, i carichi dati dalla normativa, dei tramezzi (1KN/m²) e degli impianti (0,5KN/m²)

TOTALE= (0,18 + 0,1872 + 0,5625 + 0,54 + 1,7 +0,175 + 1 + 0,5) KN/m² = 4,85 KN/m²

Analisi dei carichi accidentali qa

Ambiente ad uso residenziale (Normativa)

TOTALE = 2KN/m²

Dopo aver inserito i carichi nella tabella Excel, scegliamo il legno GL 24h con resitenza a flessione fm,k = 24MPa, si troverà quindi la sigma ammissibile. Impostando la base b=30cm si troverà l'altezza H= 51,40cm.

Si prenderà quindi una sezione pari a 30cmx55cm e si calcolerà il peso proprio p della trave.

p= (0,30m x 0,55m x 1m)/m x 7KN/m³= 1,155 KN/m

La sezione precedentemente dimensionata risulta verificata.

LA TRAVE RETICOLARE

STRUTTURA RETICOLARE IN 2D - SAP

Voglio verificare la struttura reticolare calcolata precedentemente a mano.

1- File --> New Model --> 2D Trusses

                                        - Number of division (numero delle aste di base) --> 3

                                        - Height (altezza) --> 3 (nell'esercizio precedente era L)

                                        - Division Lenght (lunghezza delle aste di base) --> 6 (nell'esercizio a mano era 2L)

Si aprirà quindi questa trave reticolare:

2- Bisogna inserire nei nodi delle cerniere interne in modo tale che il momento ai nodi sia nullo.

- Selezionare le aste

- Assign --> Frame --> Releases/ Partial Fixity

                                 - Spuntare Momento 33 (Major) sia Start che End (in modo tale da imporre che il

                                   momento all'inizio e alla fine di ogni asta sia nullo).

3- Selezionare i nodi sui quali vanno inseriti i carichi puntuali (F)

- Assign --> Joint Loads --> Forces

- Load Pattern name [+] --> Rinominare Es. F

                                         - Self Weight Multiplier --> 0 (non si sta prendendo in considerazione il peso proprio

                                           della struttura).

                                          - Add New Load Pattern

- Load Pattern Name --> F

- Force Global Z (asse verticale) --> -100 (inserendo il -, si sta dicendo che il carico verticale è rivolto verso il basso)

Si avrà quindi questa situazione:

4- Ora bisogna quindi inserire i materiali

- Selezionare tutto

- Assign --> Frame --> Frame Sections --> Add New Property

                                                                - Frame Section Type (materiale) --> Steel (acciaio)

                                                                - Add a steel section --> Pipe (Tubolare)

                                                                - Section Name (nome della sezione) --> Es. Tubolare

5- Avviare l'analisi --> Run/ Do not Run Case per Dead e Modal, di cui non si vuole fare l'analisi

                                   --> Run Now --> Salvare il File

6- Vedere il diagramma degli sforzi assiali

- Show Forces/Stresses --> Frame/Cables/Tendons

                                            - Case --> Combo Name --> F

                                            - Component --> Axial Force 

                                            - Options --> Show Values on Diagram (per mostrare i valori sul diagramma)

7- E' possibile assegnare un nome alle aste in modo tale da poter associare l'asta al frame della tabella Excel.

- Set Display Options 

8- Esportare la tabella in Excel

- File --> Export --> SAP2000 Excel Spreadsheet.xsl File

STRUTTURA RETICOLARE IN 3D - SAP

Dopo la realizzazione di una struttura reticolare in 2D su SAP, sono passata alla realizzazione di una struttura reticolare in 3D.

1- Aprire un Nuovo File --> Grid Only: Number of Grid Lines

                                           - X direction 11

                                           - Y direction 11

                                           - Z direction 2

Si aprirà quindi una griglia che ci aiuterà a disegnare la struttura reticolare.

2- Utilizzare lo strumento Draw Frame e disegnare le aste, aiutandosi con le griglie. Dopo aver disegnato un primo modulo, copiare CTRL-C e incollare CTRL-V fino a riempire la griglia.

3- Per sicurezza, dopo aver riempito la griglia, selezionare tutto --> Edit --> Edit Points --> Merge Joints. Questo passaggio serve a riunire i nodi che durante il copia-incolla possono essersi spostati.

4- Inserire i vincoli selezionando i nodi --> assign --> Joint (vincolo) --> Restraints

5- Ripetere i punti della trave reticolare 2D per inserire le cerniere interne, mettere i carichi e inserire il materiale.

6- Avviare l'analisi dei carichi

7- Si può quindi procedere alla visione del diagramma degli sforzi normali. (Se si procede nella visione dei diagrammi del taglio e del momento ci si accorgerà che sono nulli).

Esportiamo quindi la tabella in Excel

CENTRE POMPIDOU - Parigi